上海市浦东新区部分学校2022-2023学年六年级(五四学制)下学期期末数学试题(无答案)
文档属性
| 名称 | 上海市浦东新区部分学校2022-2023学年六年级(五四学制)下学期期末数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 00:18:40 | ||
图片预览

文档简介
2023学年第二学期 期末质量检测
六年级 数学学科 试卷
(完卷时间90分钟 满分100分)
一、选择题(本大题共6小题,每小题2分,共12分)
1. 下列说法正确的是( )
A. 一个有理数非负即正 B.的值与的值相等
C. 两点之间的连线中,直线最短 D. 若点P是线段AB的中点,则
2. 若,且c为有理数,则( )
A. B. C. D.
3. 四点这一时刻,分针和时针的夹角是( )
A. B. C. D.
4. 如图,直线AB,CD相交于点O,OA平分∠COE,,则∠AOE的度数是( )
A. B. C. D.
5. 某年级学生共有246人,其中男生人数y比女生人数x的2倍少2人,则下面所列的方程组中符合题意的有( )
A. B. C. D.
6. 将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. B. C. D.
二、填空题(本大题共12小题,每小题2分,共24分)
7. -0.4的倒数是___.
8. 计算:___.
9. 比较大小:-___
10. 满足不等式的非负整数解的和是___.
11. 由于全球经济的影响,5月中旬全国各大银行一年期利率又有所下调,如××银行一年期利率由2.5%降至1.9%.若王先生现在存入10万元,定期一年,将少获得___元利息.
12. “方程”二字最早见于我国《九章算术》这部经典著作中,该书的第八章名为“方程”如:从左到右列出的算筹数分别表示方程中未知数x、y的系数与相应的常数项,即可表示方程,则表示的方程是___.
13. 随着我国新经济的不断推进,我国人工智能行业规模持续增长,预计2023年我国人工智能市场规模将达到3200亿元人民币,同比增长33.8%.用科学记数法表示“320000000000”为___.
14. 在直线AB上有一点C,已知,则AC等于___.
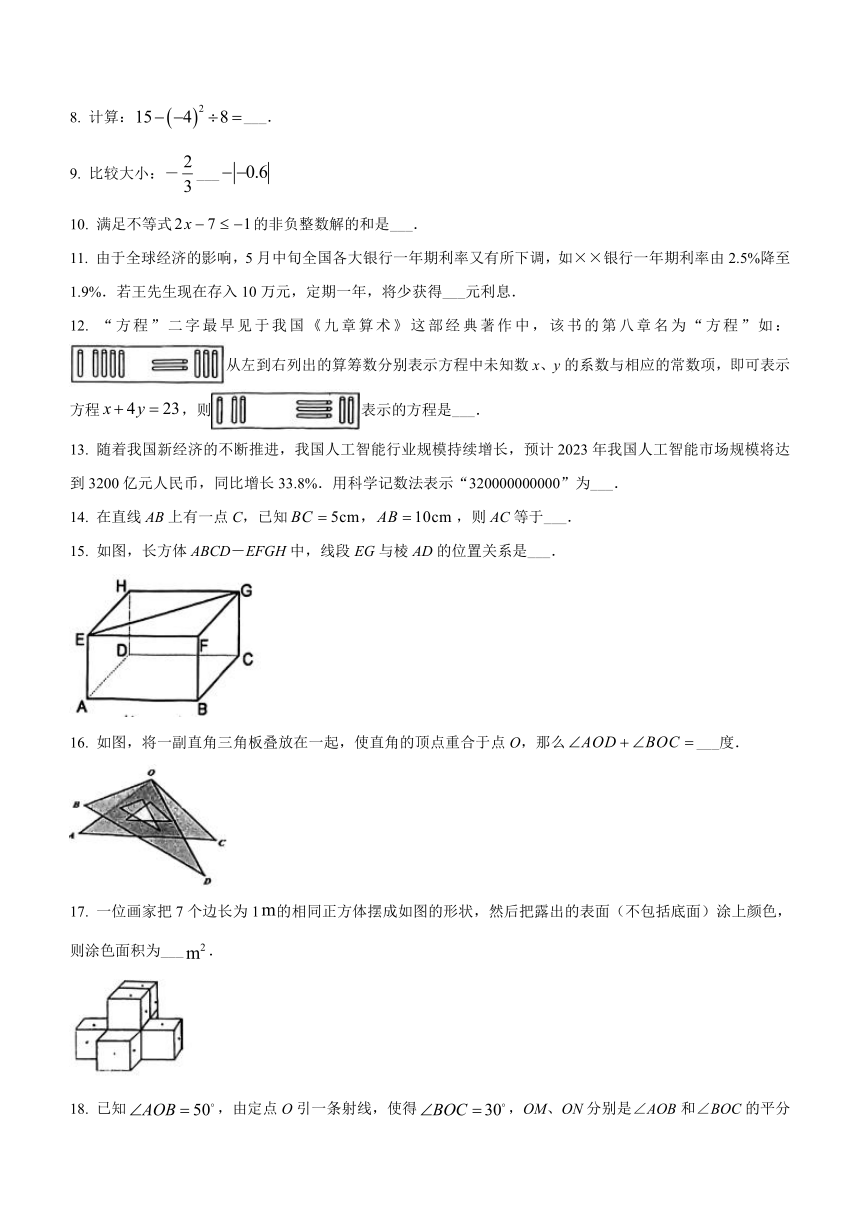
15. 如图,长方体ABCD-EFGH中,线段EG与棱AD的位置关系是___.
16. 如图,将一副直角三角板叠放在一起,使直角的顶点重合于点O,那么___度.
17. 一位画家把7个边长为1的相同正方体摆成如图的形状,然后把露出的表面(不包括底面)涂上颜色,则涂色面积为___.
18. 已知,由定点O引一条射线,使得,OM、ON分别是∠AOB和∠BOC的平分线,则∠MON=___度.
三、简答题(本大题共6小题,每小题5分,共30分)
19. 计算:
20. 解方程:
21. 解方程组:
22. 解不等式:,并把它的解集在数轴上表示出来.
23. 求不等式组的整数解.
24. 解方程组:
四、画图题(本大题共2小题,每小题6分,共12分)
25.(1)补全下列图形,使之成为长方体的直观图(不必写画法).
(2)结合图形,回答下列问题:
与棱AB垂直的平面有___个;这个长方体所有棱长和为36cm,如果长比高多1cm,宽比高少1cm,那么这个长方体的高是___cm.
26. 已知,如图,点C在∠AOB的内部,且,OP是∠AOB的角平分线.
(1)尺规作图:作∠AOB的角平分线OP(不写作法,保留作图痕迹);
(2)若射线OC、OA分别表示从点O出发的正东、正北两个方向,则射线OB表示的方向是___;
(3)在图中找出∠AOB互补的角是___.
五、解答题(本大题共3题,第27题6分,第28题6分,第29题10分,共22分)
27. 我们规定,若关于x的一元一次方程的解为,则称该方程为“奇异方程”.例如:的解为,则该方程是“奇异方程”.请根据上述规定解答下列问题:
(1)判断方程___(回答“是”或“不是”)“奇异方程”;
(2)若,有符合要求的“奇异方程”吗?若有,求b的值;若没有,请说明理由.
28. 已知A、B、C三点在数轴上的位置如图所示,点C表示的数为6,,.
(1)数轴上点A表示的数为___,点B表示的数为___;
(2)动点P、Q分别从A,C同时出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动.点Q以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t()秒;
①求数轴上点P,Q表示的数(用含t的式子表示);
②请直接写出t为何值时,P、Q两点相距5个单位长度.
29. 宁波杨梅季,某杨梅种植大户为了能让居民品尝到物美价廉的杨梅,对1000斤的杨梅进行打包方式优惠出售,打包方式及售价如下:圆篮每篮8斤,售价160元;方篮每篮18斤,售价270元.假如用这两种打包方式恰好全部装完这1000斤杨梅.
(1)若这批杨梅全部售完,销售总收入为16760元,请问圆篮共包装了多少篮,方篮共包装了多少篮?
(2)若杨梅大户留下b()篮圆篮送人,其余的杨梅全部售出,销售总收入为16760元,求b的值.
六年级 数学学科 试卷
(完卷时间90分钟 满分100分)
一、选择题(本大题共6小题,每小题2分,共12分)
1. 下列说法正确的是( )
A. 一个有理数非负即正 B.的值与的值相等
C. 两点之间的连线中,直线最短 D. 若点P是线段AB的中点,则
2. 若,且c为有理数,则( )
A. B. C. D.
3. 四点这一时刻,分针和时针的夹角是( )
A. B. C. D.
4. 如图,直线AB,CD相交于点O,OA平分∠COE,,则∠AOE的度数是( )
A. B. C. D.
5. 某年级学生共有246人,其中男生人数y比女生人数x的2倍少2人,则下面所列的方程组中符合题意的有( )
A. B. C. D.
6. 将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A. B. C. D.
二、填空题(本大题共12小题,每小题2分,共24分)
7. -0.4的倒数是___.
8. 计算:___.
9. 比较大小:-___
10. 满足不等式的非负整数解的和是___.
11. 由于全球经济的影响,5月中旬全国各大银行一年期利率又有所下调,如××银行一年期利率由2.5%降至1.9%.若王先生现在存入10万元,定期一年,将少获得___元利息.
12. “方程”二字最早见于我国《九章算术》这部经典著作中,该书的第八章名为“方程”如:从左到右列出的算筹数分别表示方程中未知数x、y的系数与相应的常数项,即可表示方程,则表示的方程是___.
13. 随着我国新经济的不断推进,我国人工智能行业规模持续增长,预计2023年我国人工智能市场规模将达到3200亿元人民币,同比增长33.8%.用科学记数法表示“320000000000”为___.
14. 在直线AB上有一点C,已知,则AC等于___.
15. 如图,长方体ABCD-EFGH中,线段EG与棱AD的位置关系是___.
16. 如图,将一副直角三角板叠放在一起,使直角的顶点重合于点O,那么___度.
17. 一位画家把7个边长为1的相同正方体摆成如图的形状,然后把露出的表面(不包括底面)涂上颜色,则涂色面积为___.
18. 已知,由定点O引一条射线,使得,OM、ON分别是∠AOB和∠BOC的平分线,则∠MON=___度.
三、简答题(本大题共6小题,每小题5分,共30分)
19. 计算:
20. 解方程:
21. 解方程组:
22. 解不等式:,并把它的解集在数轴上表示出来.
23. 求不等式组的整数解.
24. 解方程组:
四、画图题(本大题共2小题,每小题6分,共12分)
25.(1)补全下列图形,使之成为长方体的直观图(不必写画法).
(2)结合图形,回答下列问题:
与棱AB垂直的平面有___个;这个长方体所有棱长和为36cm,如果长比高多1cm,宽比高少1cm,那么这个长方体的高是___cm.
26. 已知,如图,点C在∠AOB的内部,且,OP是∠AOB的角平分线.
(1)尺规作图:作∠AOB的角平分线OP(不写作法,保留作图痕迹);
(2)若射线OC、OA分别表示从点O出发的正东、正北两个方向,则射线OB表示的方向是___;
(3)在图中找出∠AOB互补的角是___.
五、解答题(本大题共3题,第27题6分,第28题6分,第29题10分,共22分)
27. 我们规定,若关于x的一元一次方程的解为,则称该方程为“奇异方程”.例如:的解为,则该方程是“奇异方程”.请根据上述规定解答下列问题:
(1)判断方程___(回答“是”或“不是”)“奇异方程”;
(2)若,有符合要求的“奇异方程”吗?若有,求b的值;若没有,请说明理由.
28. 已知A、B、C三点在数轴上的位置如图所示,点C表示的数为6,,.
(1)数轴上点A表示的数为___,点B表示的数为___;
(2)动点P、Q分别从A,C同时出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动.点Q以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t()秒;
①求数轴上点P,Q表示的数(用含t的式子表示);
②请直接写出t为何值时,P、Q两点相距5个单位长度.
29. 宁波杨梅季,某杨梅种植大户为了能让居民品尝到物美价廉的杨梅,对1000斤的杨梅进行打包方式优惠出售,打包方式及售价如下:圆篮每篮8斤,售价160元;方篮每篮18斤,售价270元.假如用这两种打包方式恰好全部装完这1000斤杨梅.
(1)若这批杨梅全部售完,销售总收入为16760元,请问圆篮共包装了多少篮,方篮共包装了多少篮?
(2)若杨梅大户留下b()篮圆篮送人,其余的杨梅全部售出,销售总收入为16760元,求b的值.
同课章节目录
