辽宁省阜新市第二高级中学2022-2023学年高一下学期期中考试数学试卷(含解析)
文档属性
| 名称 | 辽宁省阜新市第二高级中学2022-2023学年高一下学期期中考试数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 330.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-22 05:51:33 | ||
图片预览



文档简介
阜新市第二高级中学2022-2023学年高一下学期期中考试
数学试卷
一、选择题( 单选题,每题只有一个正确答案,每题5分 )
1、集合还可以表示为( )。
A. B. C. D.
2、复数(其中i为虚数单位),则( )。
A. B.2 C. D.5
3、下列化简结果错误的是( )。
A. B.
C. D.
4、异面直线是指( )。
A.空间中两条不相交的直线 B.分别位于两个不同平面内的两条直线
C.平面内的一条直线与平面外的一条直线 D.不同在任何一个平面内的两条直线
5、函数的最小正周期是( )。
A. B. C. D.
6、在中,A,B,C的对边分别是a,b,c,若,
则的形状是( )。
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角或直角三角形
7、 ( )。
A. B. C. D.
8、若,则( )。
A. B. C. D.
二、多项选择题(每题5分 ,全部选对得5分,部分选对得2分,选错不得分)
9、设,则( )。
A.是偶函数 B.是奇函数 C.没有零点 D.有零点
10、下列说法错误的是( )。
A.复数不是纯虚数
B.若,则复数是纯虚数
C.若是纯虚数,则实数
D.若复数,则当且仅当时,z为虚数
11、下列说法中不正确的是( )。
A.棱柱的侧面可以是三角形 B.正方体和长方体都是特殊的四棱柱
C.所有几何体的表面都能展开成平面图形 D.棱柱的各条棱都相等
12、下列叙述中错误的是( )。
A.若,则 B.若,则与的方向相同或相反
C.若,,则 D.对任一向量,是一个单位向量
三、填空题(每题5分)
13、根式__________。
14、幂函数的图象经过点,则值为____________。
15、已知,函数的最小值为_________。
16、不等式 的解集为__________。
四、解答题(17题10分,其余每题12分)
17、(本题10分)已知函数。
(1)求的值; (2)求的值。
18、(本题12分)
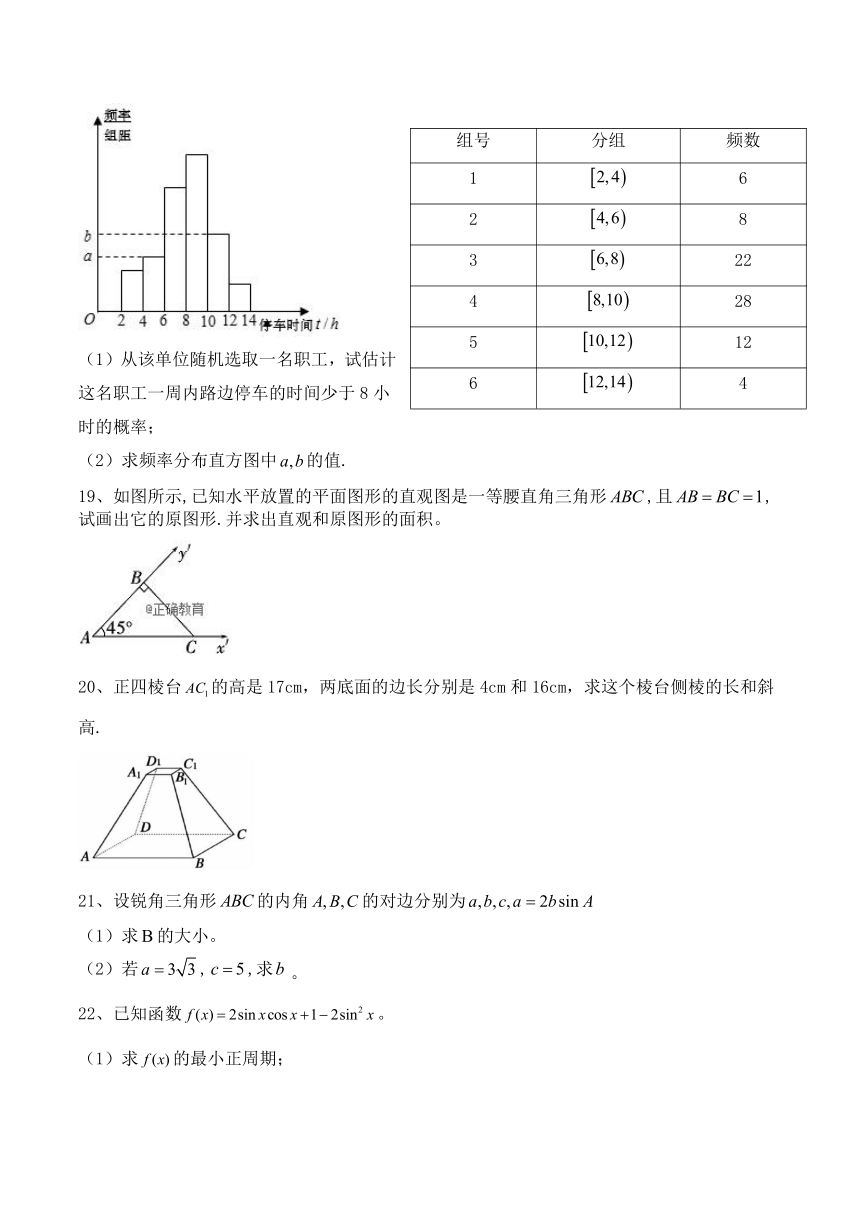
为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:
组号 分组 频数
1 6
2 8
3 22
4 28
5 12
6 4
(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中的值.
19、如图所示,已知水平放置的平面图形的直观图是一等腰直角三角形,且,试画出它的原图形.并求出直观和原图形的面积。
20、正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高.
21、设锐角三角形的内角的对边分别为
(1)求的大小。
(2)若,,求。
22、已知函数。
(1)求的最小正周期;
(2)求在区间上的最大值与最小值。
参考答案
1、答案:A
解析:集合的元素为小于3的全部非负整数,则;所以A选项是正确的.
2、答案:A
解析:,则.
故选:A.
3、答案:D
解析:对A,原式,正确;
对B,原式,正确;
对C,原式,正确;
对D,原式,错误.
故选:D.
4、答案:D
解析:对于A,空间中两条不相交的直线有两种可能,一个是平行(共面),另一个是异面,所以A应排除.对于B,分别位于两个不同平面内的直线,既可能平行也可能相交也可能异面,如图,就是相交的情况,所以B应排除.对于C,如图中的a,b可看作是平面内的一条直线a与平面外的一条直线b,显然它们是相交直线,所以C应排除.只有D符合定义.
5、答案:B
解析:函数的最小正周期是;
故选:B.
6、答案:C
解析:三角形ABC中,,所以C为钝角,
三角形为钝角三角形.
故选:C.
7、答案:D
解析:
8、答案:D
解析:
9、答案:BD
解析:
10、答案:ACD
解析:,时,复数是纯虚数,A错误;
当时,复数是纯虚数,B正确;
是纯虚数,则即,C错误;
复数,a,b未注明为实数,D错误.
故选:ACD.
11、答案:ACD
解析:棱柱的侧面都是四边形,A不正确;正方体和长方体都是特殊的四棱柱,B正确;不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;棱柱的各条棱并不是都相等,应该为棱柱的侧棱都相等,D不正确.故选ACD.
12、答案:ABCD
解析:因为是既有大小又有方向的量,所以向量不能比较大小,故A错误;
由于零向量与任意向量共线,且零向量的方向是任意的,故B错误;
对于C,若为零向量,则与可能不是共线向量,故C错误;
对于D,当时,无意义,故D错误.
故选:ABCD.
13、答案:
解析:
14、答案:9
解析:令幂函数解析式为,又幂函数的图象过点,,,幂函数的解析式为,所以9.
15、答案:4
解析:因为,所以,
当且仅当,即时等号成立,因此所求的最小值为4
16、答案:
解析:
17、答案:(1)因为,所以。因为,所以。
(2)依题意,知。
解析:
18、答案:1.记 “从该单位随机选取一名职工,这名职工该周路边停车的时间少于8小时”为事件A,
则;
2. ,
解析:
19、答案:
20、答案:棱台的侧棱长为19cm,斜高为cm
解析:解:如图所示,设棱台的两底面的中心分别是和O,和BC的中点分别是和E,连接,,,OB,,OE,则四边形和都是直角梯形.
,,
,,,.
,
.
,.
即棱台的侧棱长为19cm,斜高为cm.
21、答案:1.由,根据正弦定理得,
所以,由△为锐角三角形得
2.根据余弦定理,得.
所以, .
22、答案:(1)因为,所以的最小正周期为.
(2)因为,所以.当,即时,取得最大值;当,即时,,即的最小值为.
数学试卷
一、选择题( 单选题,每题只有一个正确答案,每题5分 )
1、集合还可以表示为( )。
A. B. C. D.
2、复数(其中i为虚数单位),则( )。
A. B.2 C. D.5
3、下列化简结果错误的是( )。
A. B.
C. D.
4、异面直线是指( )。
A.空间中两条不相交的直线 B.分别位于两个不同平面内的两条直线
C.平面内的一条直线与平面外的一条直线 D.不同在任何一个平面内的两条直线
5、函数的最小正周期是( )。
A. B. C. D.
6、在中,A,B,C的对边分别是a,b,c,若,
则的形状是( )。
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角或直角三角形
7、 ( )。
A. B. C. D.
8、若,则( )。
A. B. C. D.
二、多项选择题(每题5分 ,全部选对得5分,部分选对得2分,选错不得分)
9、设,则( )。
A.是偶函数 B.是奇函数 C.没有零点 D.有零点
10、下列说法错误的是( )。
A.复数不是纯虚数
B.若,则复数是纯虚数
C.若是纯虚数,则实数
D.若复数,则当且仅当时,z为虚数
11、下列说法中不正确的是( )。
A.棱柱的侧面可以是三角形 B.正方体和长方体都是特殊的四棱柱
C.所有几何体的表面都能展开成平面图形 D.棱柱的各条棱都相等
12、下列叙述中错误的是( )。
A.若,则 B.若,则与的方向相同或相反
C.若,,则 D.对任一向量,是一个单位向量
三、填空题(每题5分)
13、根式__________。
14、幂函数的图象经过点,则值为____________。
15、已知,函数的最小值为_________。
16、不等式 的解集为__________。
四、解答题(17题10分,其余每题12分)
17、(本题10分)已知函数。
(1)求的值; (2)求的值。
18、(本题12分)
为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:
组号 分组 频数
1 6
2 8
3 22
4 28
5 12
6 4
(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中的值.
19、如图所示,已知水平放置的平面图形的直观图是一等腰直角三角形,且,试画出它的原图形.并求出直观和原图形的面积。
20、正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高.
21、设锐角三角形的内角的对边分别为
(1)求的大小。
(2)若,,求。
22、已知函数。
(1)求的最小正周期;
(2)求在区间上的最大值与最小值。
参考答案
1、答案:A
解析:集合的元素为小于3的全部非负整数,则;所以A选项是正确的.
2、答案:A
解析:,则.
故选:A.
3、答案:D
解析:对A,原式,正确;
对B,原式,正确;
对C,原式,正确;
对D,原式,错误.
故选:D.
4、答案:D
解析:对于A,空间中两条不相交的直线有两种可能,一个是平行(共面),另一个是异面,所以A应排除.对于B,分别位于两个不同平面内的直线,既可能平行也可能相交也可能异面,如图,就是相交的情况,所以B应排除.对于C,如图中的a,b可看作是平面内的一条直线a与平面外的一条直线b,显然它们是相交直线,所以C应排除.只有D符合定义.
5、答案:B
解析:函数的最小正周期是;
故选:B.
6、答案:C
解析:三角形ABC中,,所以C为钝角,
三角形为钝角三角形.
故选:C.
7、答案:D
解析:
8、答案:D
解析:
9、答案:BD
解析:
10、答案:ACD
解析:,时,复数是纯虚数,A错误;
当时,复数是纯虚数,B正确;
是纯虚数,则即,C错误;
复数,a,b未注明为实数,D错误.
故选:ACD.
11、答案:ACD
解析:棱柱的侧面都是四边形,A不正确;正方体和长方体都是特殊的四棱柱,B正确;不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;棱柱的各条棱并不是都相等,应该为棱柱的侧棱都相等,D不正确.故选ACD.
12、答案:ABCD
解析:因为是既有大小又有方向的量,所以向量不能比较大小,故A错误;
由于零向量与任意向量共线,且零向量的方向是任意的,故B错误;
对于C,若为零向量,则与可能不是共线向量,故C错误;
对于D,当时,无意义,故D错误.
故选:ABCD.
13、答案:
解析:
14、答案:9
解析:令幂函数解析式为,又幂函数的图象过点,,,幂函数的解析式为,所以9.
15、答案:4
解析:因为,所以,
当且仅当,即时等号成立,因此所求的最小值为4
16、答案:
解析:
17、答案:(1)因为,所以。因为,所以。
(2)依题意,知。
解析:
18、答案:1.记 “从该单位随机选取一名职工,这名职工该周路边停车的时间少于8小时”为事件A,
则;
2. ,
解析:
19、答案:
20、答案:棱台的侧棱长为19cm,斜高为cm
解析:解:如图所示,设棱台的两底面的中心分别是和O,和BC的中点分别是和E,连接,,,OB,,OE,则四边形和都是直角梯形.
,,
,,,.
,
.
,.
即棱台的侧棱长为19cm,斜高为cm.
21、答案:1.由,根据正弦定理得,
所以,由△为锐角三角形得
2.根据余弦定理,得.
所以, .
22、答案:(1)因为,所以的最小正周期为.
(2)因为,所以.当,即时,取得最大值;当,即时,,即的最小值为.
同课章节目录
