北师大版数学八年级下册 3.3 中心对称课件(共16张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 3.3 中心对称课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 13:36:10 | ||
图片预览






文档简介
(共16张PPT)
数学八年级下册 BS
第 三 章 图形的平移与旋转
3 中心对称
问题思考
什么是旋转
旋转的意义:在平面内,将一个图形绕着一个定点按某个方向旋转一定的角度,这样的图形运动称为旋转.这个定点称为旋转中心,转动的角称为旋转角.图形的旋转不改变图形的形状和大小.
学习新知
旋转具有什么性质
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等.
你能用旋转的思想描述下列两个图形的位置关系吗
相关的定义
观察下图,图(1)经过怎样的运动变化就可以与图(2)重合 观察下图,
再试一试.你还能举出一些类似的例子吗 与同伴交流.
中心对称的定义:如果一个图形绕着某一点旋转180°,它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
如图所示,△ABC与△A'B'C'成中心对称,点O是它们的对称中心.
例 如图所示,点O 是线段AE的中点,以点O为对称
中心,画出与五边形ABCDE成中心对称的图形.
【解析】 已知一个图形和对称中心,画与它成中心对称的图形,实际上就是把已知图形绕对称中心旋转180°.但利用中心对称的特征,可以不用旋转而更为快捷地画出图形.
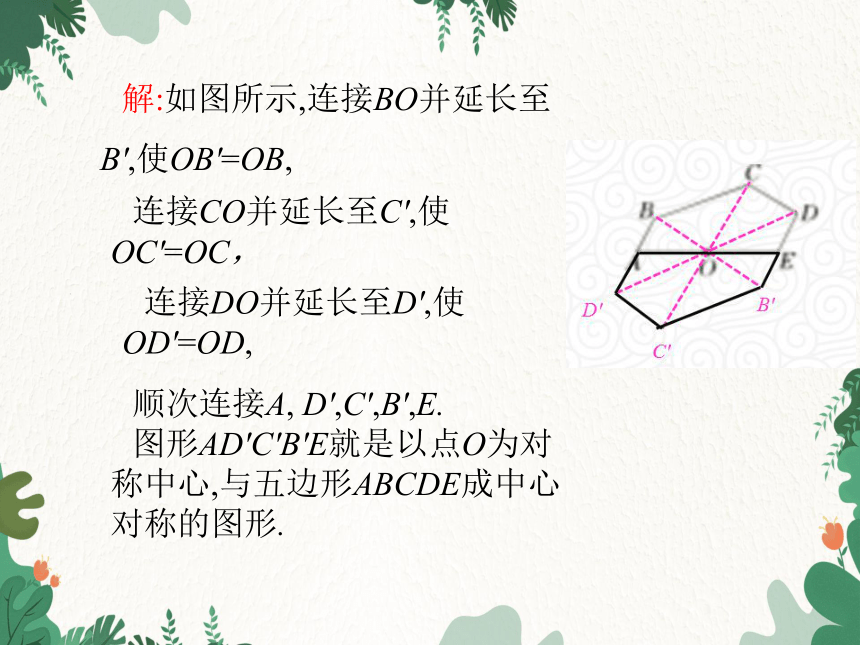
解:如图所示,连接BO并延长至B',使OB'=OB,
顺次连接A, D',C',B',E.
图形AD'C'B'E就是以点O为对称中心,与五边形ABCDE成中心对称的图形.
连接CO并延长至C',使OC'=OC,
连接DO并延长至D',使OD'=OD,
区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
中心对称与中心对称图形的联系与区别.
知识拓展
观察下图,这些图形有什么共同特征 你能举出一些类似的图形吗
中心对称图形的定义:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
中心对称的性质
【问题1】 如图所示,点A与点A'关于点O对称,连接
AA',你能发现什么
(1)点A绕点O旋转180°后与点A'重合;
(2)OA=OA';
(3)∠AOA'=180°,即点O在AA'上.
【问题2】 如图所示,四边形ABCD与四边形A'B'C'D'关于点O对称,分别连接AA',BB',CC',DD',你发现了什么
(1)AA',BB',CC',DD'都经过点O.
(2)OA=OA',OB=OB', OC=OC', OD=OD'.
【结论】 成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
1.将如图所示的图案以圆心为中心,旋转180°后得到的图案是 ( )
【解析】将如图所示的图案以圆心为中心,旋转180°后得到的图案与原图形成中心对称,它是 .故选D.
D
检测反馈
【解析】因为平移的距离是边BC长的两倍,则AD=2BC,点C 为BE的中点,所以四边形ACED的面积为△ABC面积的3倍,所以四边形ACED的面积为36 cm2.故填36.
2.如图所示,面积为12 cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为 cm2.
36
3.下列图形均可以由“基本图案”通过变换得到.(填序号)
(1)可以通过平移变换但不能通过旋转变换得到的图案是 ;
(2) 可以通过旋转变换但不能通过平移变换得到的图案是 ;
(3) 既可以由平移变换,也可以由旋转变换得到的图案是 .
①
②⑤
③④
4.如图所示,把△ABC向右平移5个方格,再绕点B的对应点顺时针方向旋转90°.
(1)画出平移和旋转后的图形,并标明对应字母;
(2)能否把两次变换合成一种变换 如果能,说出变换过程(可适当在图形中标记);如果不能,说明理由.
解:(1)如图所示.
(2)能,将△ABC绕CB,C″B″延长线的交点顺时针旋转90°.
数学八年级下册 BS
第 三 章 图形的平移与旋转
3 中心对称
问题思考
什么是旋转
旋转的意义:在平面内,将一个图形绕着一个定点按某个方向旋转一定的角度,这样的图形运动称为旋转.这个定点称为旋转中心,转动的角称为旋转角.图形的旋转不改变图形的形状和大小.
学习新知
旋转具有什么性质
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等.
你能用旋转的思想描述下列两个图形的位置关系吗
相关的定义
观察下图,图(1)经过怎样的运动变化就可以与图(2)重合 观察下图,
再试一试.你还能举出一些类似的例子吗 与同伴交流.
中心对称的定义:如果一个图形绕着某一点旋转180°,它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
如图所示,△ABC与△A'B'C'成中心对称,点O是它们的对称中心.
例 如图所示,点O 是线段AE的中点,以点O为对称
中心,画出与五边形ABCDE成中心对称的图形.
【解析】 已知一个图形和对称中心,画与它成中心对称的图形,实际上就是把已知图形绕对称中心旋转180°.但利用中心对称的特征,可以不用旋转而更为快捷地画出图形.
解:如图所示,连接BO并延长至B',使OB'=OB,
顺次连接A, D',C',B',E.
图形AD'C'B'E就是以点O为对称中心,与五边形ABCDE成中心对称的图形.
连接CO并延长至C',使OC'=OC,
连接DO并延长至D',使OD'=OD,
区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
中心对称与中心对称图形的联系与区别.
知识拓展
观察下图,这些图形有什么共同特征 你能举出一些类似的图形吗
中心对称图形的定义:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
中心对称的性质
【问题1】 如图所示,点A与点A'关于点O对称,连接
AA',你能发现什么
(1)点A绕点O旋转180°后与点A'重合;
(2)OA=OA';
(3)∠AOA'=180°,即点O在AA'上.
【问题2】 如图所示,四边形ABCD与四边形A'B'C'D'关于点O对称,分别连接AA',BB',CC',DD',你发现了什么
(1)AA',BB',CC',DD'都经过点O.
(2)OA=OA',OB=OB', OC=OC', OD=OD'.
【结论】 成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
1.将如图所示的图案以圆心为中心,旋转180°后得到的图案是 ( )
【解析】将如图所示的图案以圆心为中心,旋转180°后得到的图案与原图形成中心对称,它是 .故选D.
D
检测反馈
【解析】因为平移的距离是边BC长的两倍,则AD=2BC,点C 为BE的中点,所以四边形ACED的面积为△ABC面积的3倍,所以四边形ACED的面积为36 cm2.故填36.
2.如图所示,面积为12 cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为 cm2.
36
3.下列图形均可以由“基本图案”通过变换得到.(填序号)
(1)可以通过平移变换但不能通过旋转变换得到的图案是 ;
(2) 可以通过旋转变换但不能通过平移变换得到的图案是 ;
(3) 既可以由平移变换,也可以由旋转变换得到的图案是 .
①
②⑤
③④
4.如图所示,把△ABC向右平移5个方格,再绕点B的对应点顺时针方向旋转90°.
(1)画出平移和旋转后的图形,并标明对应字母;
(2)能否把两次变换合成一种变换 如果能,说出变换过程(可适当在图形中标记);如果不能,说明理由.
解:(1)如图所示.
(2)能,将△ABC绕CB,C″B″延长线的交点顺时针旋转90°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
