圆和圆和位置关系[上学期]
图片预览





文档简介
课件19张PPT。圆和圆的位置关系沈冲中学 罗结和两圆共有五种位置关系下面我们就逐一分析两圆外离两圆外切两圆相交两圆内切两圆内含..0102符合以上两个条件的圆就叫两圆外离。定义:两圆没有公共点,且每个圆上的点都在另一个圆的
外部时,叫做两圆外离。两圆外离1.这两个圆有没有公共点?
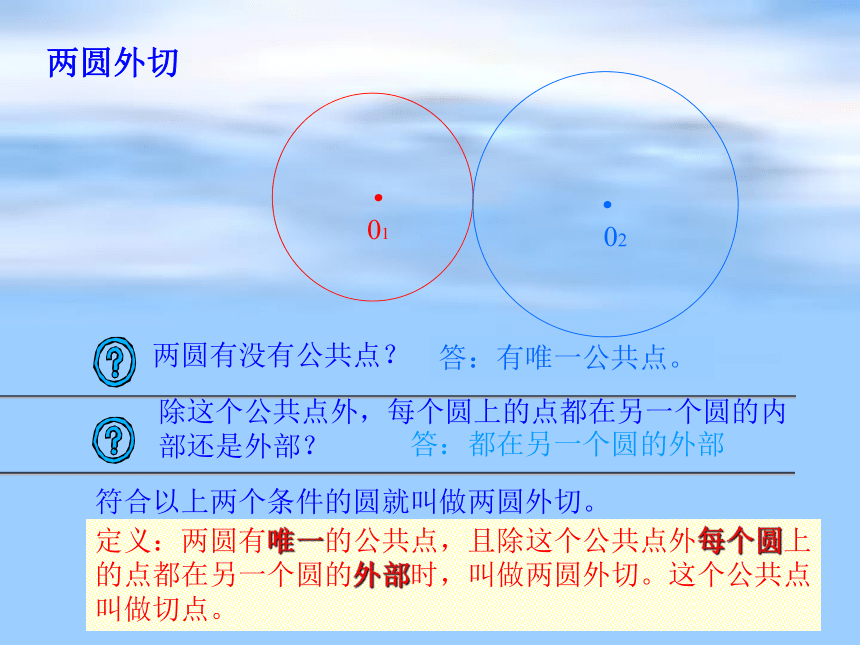
2.这两个圆的位置关系有什么特点?提示:1、没有 。2、每一个圆上的点都在另一个圆的外部。答:有唯一公共点。两圆外切答:都在另一个圆的外部符合以上两个条件的圆就叫做两圆外切。定义:两圆有唯一的公共点,且除这个公共点外每个圆上
的点都在另一个圆的外部时,叫做两圆外切。这个公共点
叫做切点。两圆有没有公共点?除这个公共点外,每个圆上的点都在另一个圆的内
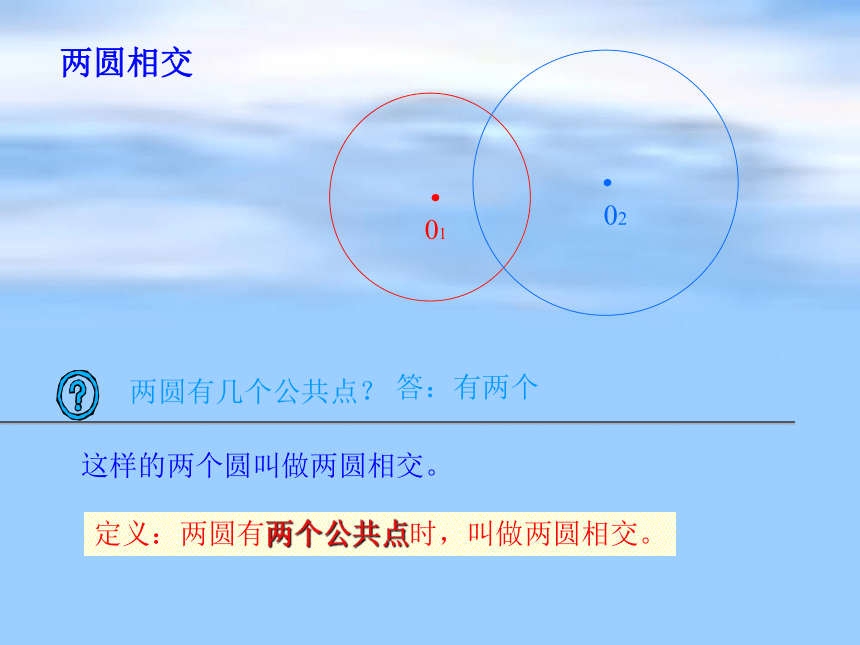
部还是外部?两圆相交答:有两个这样的两个圆叫做两圆相交。定义:两圆有两个公共点时,叫做两圆相交。两圆有几个公共点?两圆内切观察图形,结合两圆外切的定义,大家自己总结两圆内切的
定义。定义:两圆有唯一公共点,并且除这个公共点外,一圆上
的点都在另一个圆的内部时,叫做两圆内切。这个公共点叫
切点。注意:“每一圆”与“一圆”的区别两圆内含观察图形,结合两圆外离的定义,自己总结两圆内含的定义。定义:两圆没有公共点,且一圆上的点都在另一圆的内部时
叫做两圆内含。注意:1、 “一圆” 与“每一圆”的区别。
2、同心圆是内含的特例。探究思考1、两圆外离、内含有什么异同性? 相同点:两圆都没有公共点。
不同点:外离是每一圆上的点都在另一圆的外部。
内含是其中一圆上的点都在另一圆的内部。2、两圆外切、内切有什么异同性? 相同点:两圆都有唯一公共点。
不同点:外切是除公共点外,每一圆上的点
都在另一圆的外部。
内切是除公共点外,一圆上的点都在另一
圆的内部。
总结:两圆
按公共点个
数可分为理解巩固:(1)这是奥运会五环旗的旗徽
A、蓝色圆和黄色圆的关系怎样
判定?
B、蓝色圆和红色圆的关系怎样
判定?(2)“等圆的位置关系只有三种”
这种观点对吗?为什么?两 圆 位 置 关 系 的 数 量 特 征
设两圆半径分别为R和r.圆心距为d,组织学生研究两圆的五种位置关系,r和d之间有何数量关系.
02T010201.T...问题:圆是轴对称图形,那么两个圆组成的图形
是不是轴对称图形呢?如果是,对称轴是什么? 答案:是轴对称图形。对称轴是经过两圆心的直线。 定义:经过两圆心的直线叫做连心线。
两圆心之间线段的长度叫做圆心距。下面请同学们通过图形观察切点“T”与连心线的位置关系。性质:如果两圆相切,那么切点一定在连心线上。.. 例2:已知:如图△ABC中,∠C=90°,AC=12,BC=8,以AC为直径作⊙O,以B为圆心,4为半径作圆.求证:⊙O与⊙B相外切.
∴ ⊙O与⊙B相外切证明:连接OB∵ AC是⊙O的直径,AC=12∴ OC=6 ∴ 在直角△ABC中OB=
=10=4+6作业布置 课本:
1、 P-88练习1。
2、P-89练习1、2。再 见
外部时,叫做两圆外离。两圆外离1.这两个圆有没有公共点?
2.这两个圆的位置关系有什么特点?提示:1、没有 。2、每一个圆上的点都在另一个圆的外部。答:有唯一公共点。两圆外切答:都在另一个圆的外部符合以上两个条件的圆就叫做两圆外切。定义:两圆有唯一的公共点,且除这个公共点外每个圆上
的点都在另一个圆的外部时,叫做两圆外切。这个公共点
叫做切点。两圆有没有公共点?除这个公共点外,每个圆上的点都在另一个圆的内
部还是外部?两圆相交答:有两个这样的两个圆叫做两圆相交。定义:两圆有两个公共点时,叫做两圆相交。两圆有几个公共点?两圆内切观察图形,结合两圆外切的定义,大家自己总结两圆内切的
定义。定义:两圆有唯一公共点,并且除这个公共点外,一圆上
的点都在另一个圆的内部时,叫做两圆内切。这个公共点叫
切点。注意:“每一圆”与“一圆”的区别两圆内含观察图形,结合两圆外离的定义,自己总结两圆内含的定义。定义:两圆没有公共点,且一圆上的点都在另一圆的内部时
叫做两圆内含。注意:1、 “一圆” 与“每一圆”的区别。
2、同心圆是内含的特例。探究思考1、两圆外离、内含有什么异同性? 相同点:两圆都没有公共点。
不同点:外离是每一圆上的点都在另一圆的外部。
内含是其中一圆上的点都在另一圆的内部。2、两圆外切、内切有什么异同性? 相同点:两圆都有唯一公共点。
不同点:外切是除公共点外,每一圆上的点
都在另一圆的外部。
内切是除公共点外,一圆上的点都在另一
圆的内部。
总结:两圆
按公共点个
数可分为理解巩固:(1)这是奥运会五环旗的旗徽
A、蓝色圆和黄色圆的关系怎样
判定?
B、蓝色圆和红色圆的关系怎样
判定?(2)“等圆的位置关系只有三种”
这种观点对吗?为什么?两 圆 位 置 关 系 的 数 量 特 征
设两圆半径分别为R和r.圆心距为d,组织学生研究两圆的五种位置关系,r和d之间有何数量关系.
02T010201.T...问题:圆是轴对称图形,那么两个圆组成的图形
是不是轴对称图形呢?如果是,对称轴是什么? 答案:是轴对称图形。对称轴是经过两圆心的直线。 定义:经过两圆心的直线叫做连心线。
两圆心之间线段的长度叫做圆心距。下面请同学们通过图形观察切点“T”与连心线的位置关系。性质:如果两圆相切,那么切点一定在连心线上。.. 例2:已知:如图△ABC中,∠C=90°,AC=12,BC=8,以AC为直径作⊙O,以B为圆心,4为半径作圆.求证:⊙O与⊙B相外切.
∴ ⊙O与⊙B相外切证明:连接OB∵ AC是⊙O的直径,AC=12∴ OC=6 ∴ 在直角△ABC中OB=
=10=4+6作业布置 课本:
1、 P-88练习1。
2、P-89练习1、2。再 见
