人教版数学九年级 第二十六章 反比例函数水平测试 课件(共31张PPT)
文档属性
| 名称 | 人教版数学九年级 第二十六章 反比例函数水平测试 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 14:02:28 | ||
图片预览







文档简介
(共31张PPT)
模拟试卷(活页)
第二十六章 反比例函数水平测试
(时间:90分钟 满分:120分)
一、选择题(本大题10小题,每小题3分,共30分)
1. 下列函数是反比例函数的是( )
A. y=-2x B. y= C. y= D. y=x2-1
2. 在反比例函数y= 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A. k>1 B. k>0 C. k≥1 D. k<1
B
A
3. 若反比例函数y= 的图象经过点(5,-3),则该反比例函数的图象在( )
A. 第一、第二象限 B. 第一、第三象限
C. 第二、第三象限 D. 第二、第四象限
D
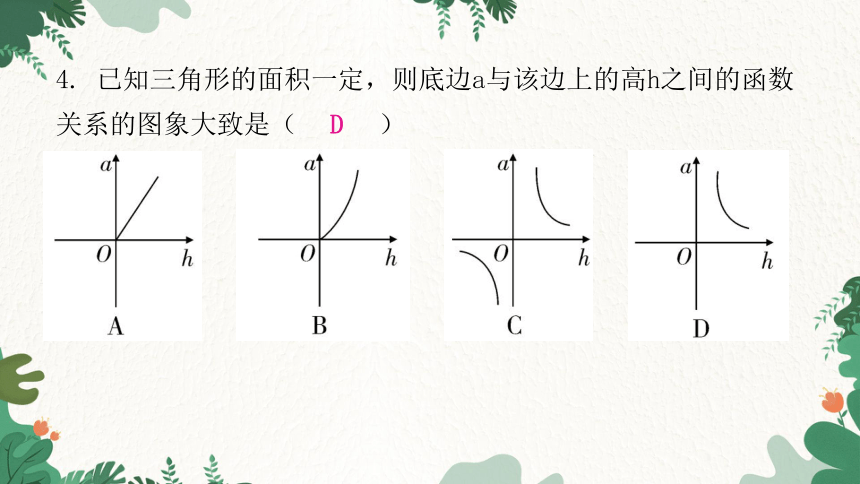
4. 已知三角形的面积一定,则底边a与该边上的高h之间的函数关系的图象大致是( )
D
5. 如果反比例函数y= 的图象经过点(-2,3),那么该函数的图象也经过点( )
A. (-2,-3) B. (3,2)
C. (3,-2) D. (-3,-2)
C
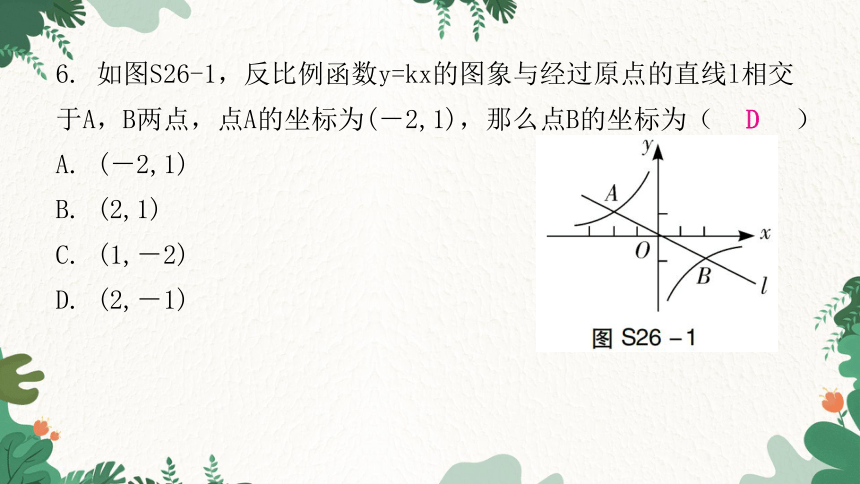
6. 如图S26-1,反比例函数y=kx的图象与经过原点的直线l相交于A,B两点,点A的坐标为(-2,1),那么点B的坐标为( )
A. (-2,1)
B. (2,1)
C. (1,-2)
D. (2,-1)
D
7. 已知点A(2,y1),B(4,y2)都在反比例函数y= 的图象上,则y1,y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
B
8. 对于反比例函数y= 下列说法不正确的是( )
A. 点(-2,-1)在它的图象上
B. 它的图象在第一、第三象限
C. 当x>0时,y随x的增大而增大
D. 当x<0时,y随x的增大而减小
C
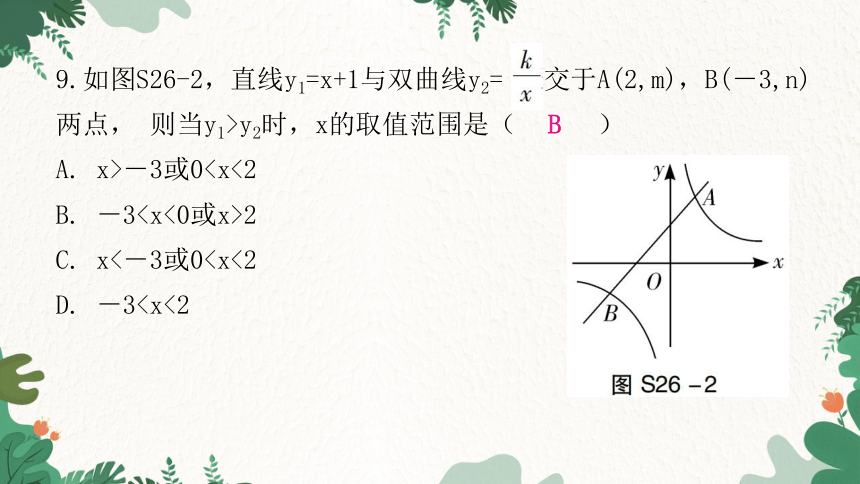
9.如图S26-2,直线y1=x+1与双曲线y2= 交于A(2,m),B(-3,n)两点, 则当y1>y2时,x的取值范围是( )
A. x>-3或0B. -32
C. x<-3或0D. -3B
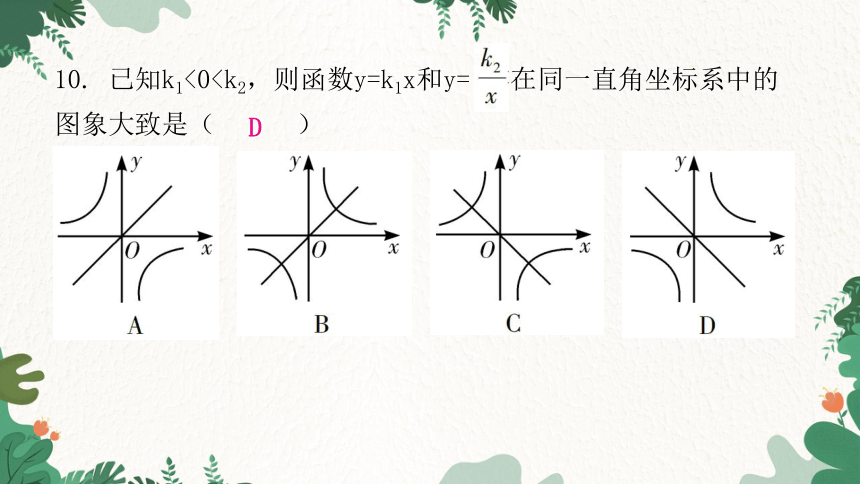
10. 已知k1<0D
二、填空题(本大题7小题,每小题4分,共28分)
11. 已知点A(1,3)关于x轴对称的点B在反比例函数y= 的图象上,则实数k的值为__________.
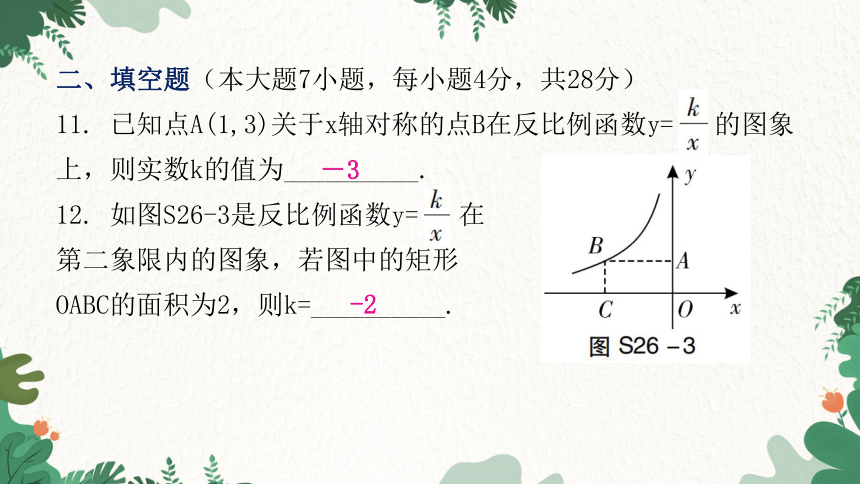
12. 如图S26-3是反比例函数y= 在
第二象限内的图象,若图中的矩形
OABC的面积为2,则k=__________.
-3
-2
13. 反比例函数y= 的图象与正比例函数y=6x的图象交于点P(m,12),则反比例函数的解析式是__________.
14. 某蓄水池的排水管的平均排水量为8 m3/h,6 h可以将满池水全部排空. 设现在的平均排水量为Q m3/h,那么将满池水排空所需要的时间为t h,则时间t与Q之间的函数表达式为__________.
>
15. 已知点A(x1,3),B(x2,6)都在反比例函数y= 的图象上,则x1__________x2.(填“<”“>”或“=”)
16. 电路上在电压保持不变的条件下,电流I(A)与电阻R(Ω)成反比例关系,I与R的函数图象如图S26-4所示,则I与R之间的函数解析式是____________________.
17. 如图S26-5,反比例函数y= (k>0)的图象经过正方形ABCD的顶点C,D.若正方形的边长为4,则k的值为__________.
16
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 已知反比例函数y= 的图象经过点A 求k的值.
解:由题意,得1-k=2×
解得k=8.
19.已知反比例函数y=
(1)当x= 时,求y的值;
(2)当自变量x取何值时,y的值为-2.
解:(1)y= (2)x=
20. 已知近视眼镜镜片的度数y(度)与镜片焦距x(m)成反比例,200度近视眼镜镜片的焦距为0.5m.
(1)求y与x的函数关系式;
(2)某学生的视力是300度近视,他需要配焦距多长的镜片?
解:(1)设y= 由题意,得k=0.5×200=100.
∴y=
(2)令y=300,即300= 解得x=
∴他需要配焦距为 m的镜片.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21. 如图S26-6,已知反比例函数y= 的图象经过点A(4,m),AB⊥x轴,垂足为点B,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y= 的
图象上,当-3≤x≤-1时,求函数值y的取值
范围.
解:(1)∵△AOB的面积为2,∴k=4.
∴反比例函数的解析式为y=
将点A(4,m)代入,得m= =1.
(2)∵当x=-3时,y= 当x=-1时,y=-4.
又∵反比例函数y= 在x<0时,y随x的增大而减小,
∴当-3≤x≤-1时,y的取值范围为-4≤y≤
22. 如图S26-7,已知一次函数y=kx+b与反比例函数y= 的图象交于A(-3,2),B(1,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
解:(1)∵反比例函数y= 的图象经过点A(-3,2),
∴m=-3×2=-6.
∴反比例函数的解析式为y=
∵点B(1,n)在反比例函数图象上,
∴n=-6.
∴B(1,-6).
把点A,B的坐标分别代入y=kx+b,得
∴一次函数的解析式为y=-2x-4.
-3k+b=2,
k+b=-6.
解得
k=-2,
b=-4.
(2)设直线AB交y轴于点C,则C(0,-4).
∴S△AOB=S△OCA+S△OCB= ×4×3+ ×4×1=8.
23. 环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许值1.0mg/L. 环保局要求该企业立即整改,在15天以内(含15天)排污达标. 整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图S26-8所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度
y与时间x的函数表达式;
(2)该企业所排污水中硫化物的
浓度,能否在15天以内达到标
准?为什么?
解:(1)根据题意,分情况讨论:
①当0≤x≤3时,设线段AB所在直线的表达式为y=kx+b(k≠0).
将点A(0,10),B(3,4)分别代入上式,得
∴y=-2x+10;
②当x>3时,设此时y与x的函数表达式为y= (k≠0).
将点B(3,4)代入上式,得4= 解得k=12. ∴y=
b=10,
3k+b=4.
解得
k=-2,
b=10.
综上所述,整改过程中硫化物的浓度y与时间x的函数表达式为
y=
-2x+10(0≤x≤3),
(x>3).
(2)能.理由如下:
当x=15时,y= =0.8<1,
∴该企业所排污水中硫化物的浓度能在15天以内达到标准.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24. 如图S26-9,一次函数y1=kx+b与反比例函数y2= 的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)P为x轴上一动点,要使PA+PB最小,
试确定点P并求出它的坐标;
(3)利用函数图象直接写出关于x的不等
式 <kx+b的解集.
解:(1)把点A(1,4)代入y2= 得m=4.
∴反比例函数的解析式为y=
把点B(4,n)代入y= ,得n=1.∴B(4,1).
把点A(1,4),B(4,1)分别代入y=kx+b,得
解得
∴一次函数的解析式为y=-x+5.
k+b=4,
4k+b=1.
k=-1,
b=5.
(2)如答图S26-1,作点B关于x轴的对称点B′,则B′
(4,-1),连接AB′交x轴于点P,此时PA+PB=AB′最小.
∴直线AB′的解析式为y=
当y=0时,x= ∴P( 0).
(3)由图像可知,关于x的不等式
<kx+b的解集是x<0或1<x<4.
25. 如图S26-10,已知点A(4,a),B(-10,-4)是一次函数y=kx+b的图象与反比例函数y= 的图象的交点,且一次函数与x轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)连接AO,求△AOB的面积;
(3)在y轴上有一点P,使得S△AOP=
S△AOC,求出点P的坐标.
解:(1)把点B(-10,-4)代入y= 得-4= 解得m=40.
∴反比例函数的解析式为y=
把点A(4,a)代入上式,得a= =10.∴A(4,10).
把点A(4,10),B(-10,-4)分别代入y=kx+b,得
解得
∴一次函数的解析式为y=x+6.
4k+b=10,
-10k+b=-4.
k=1,
b=6.
(2)在y=x+6中,令y=0,求得x=-6,∴C(-6,0).
∴S△AOB=S△AOC+S△BOC= ×6×10+ ×6×4=42.
(3)∵S△AOC= ×6×10=30,S△AOP=S△AOC,
∴ OP·xA=30,即 OP×4=30.
解得OP=15.
∴点P的坐标为(0,15)或(0,-15).
模拟试卷(活页)
第二十六章 反比例函数水平测试
(时间:90分钟 满分:120分)
一、选择题(本大题10小题,每小题3分,共30分)
1. 下列函数是反比例函数的是( )
A. y=-2x B. y= C. y= D. y=x2-1
2. 在反比例函数y= 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A. k>1 B. k>0 C. k≥1 D. k<1
B
A
3. 若反比例函数y= 的图象经过点(5,-3),则该反比例函数的图象在( )
A. 第一、第二象限 B. 第一、第三象限
C. 第二、第三象限 D. 第二、第四象限
D
4. 已知三角形的面积一定,则底边a与该边上的高h之间的函数关系的图象大致是( )
D
5. 如果反比例函数y= 的图象经过点(-2,3),那么该函数的图象也经过点( )
A. (-2,-3) B. (3,2)
C. (3,-2) D. (-3,-2)
C
6. 如图S26-1,反比例函数y=kx的图象与经过原点的直线l相交于A,B两点,点A的坐标为(-2,1),那么点B的坐标为( )
A. (-2,1)
B. (2,1)
C. (1,-2)
D. (2,-1)
D
7. 已知点A(2,y1),B(4,y2)都在反比例函数y= 的图象上,则y1,y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
B
8. 对于反比例函数y= 下列说法不正确的是( )
A. 点(-2,-1)在它的图象上
B. 它的图象在第一、第三象限
C. 当x>0时,y随x的增大而增大
D. 当x<0时,y随x的增大而减小
C
9.如图S26-2,直线y1=x+1与双曲线y2= 交于A(2,m),B(-3,n)两点, 则当y1>y2时,x的取值范围是( )
A. x>-3或0
C. x<-3或0
10. 已知k1<0
二、填空题(本大题7小题,每小题4分,共28分)
11. 已知点A(1,3)关于x轴对称的点B在反比例函数y= 的图象上,则实数k的值为__________.
12. 如图S26-3是反比例函数y= 在
第二象限内的图象,若图中的矩形
OABC的面积为2,则k=__________.
-3
-2
13. 反比例函数y= 的图象与正比例函数y=6x的图象交于点P(m,12),则反比例函数的解析式是__________.
14. 某蓄水池的排水管的平均排水量为8 m3/h,6 h可以将满池水全部排空. 设现在的平均排水量为Q m3/h,那么将满池水排空所需要的时间为t h,则时间t与Q之间的函数表达式为__________.
>
15. 已知点A(x1,3),B(x2,6)都在反比例函数y= 的图象上,则x1__________x2.(填“<”“>”或“=”)
16. 电路上在电压保持不变的条件下,电流I(A)与电阻R(Ω)成反比例关系,I与R的函数图象如图S26-4所示,则I与R之间的函数解析式是____________________.
17. 如图S26-5,反比例函数y= (k>0)的图象经过正方形ABCD的顶点C,D.若正方形的边长为4,则k的值为__________.
16
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 已知反比例函数y= 的图象经过点A 求k的值.
解:由题意,得1-k=2×
解得k=8.
19.已知反比例函数y=
(1)当x= 时,求y的值;
(2)当自变量x取何值时,y的值为-2.
解:(1)y= (2)x=
20. 已知近视眼镜镜片的度数y(度)与镜片焦距x(m)成反比例,200度近视眼镜镜片的焦距为0.5m.
(1)求y与x的函数关系式;
(2)某学生的视力是300度近视,他需要配焦距多长的镜片?
解:(1)设y= 由题意,得k=0.5×200=100.
∴y=
(2)令y=300,即300= 解得x=
∴他需要配焦距为 m的镜片.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21. 如图S26-6,已知反比例函数y= 的图象经过点A(4,m),AB⊥x轴,垂足为点B,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y= 的
图象上,当-3≤x≤-1时,求函数值y的取值
范围.
解:(1)∵△AOB的面积为2,∴k=4.
∴反比例函数的解析式为y=
将点A(4,m)代入,得m= =1.
(2)∵当x=-3时,y= 当x=-1时,y=-4.
又∵反比例函数y= 在x<0时,y随x的增大而减小,
∴当-3≤x≤-1时,y的取值范围为-4≤y≤
22. 如图S26-7,已知一次函数y=kx+b与反比例函数y= 的图象交于A(-3,2),B(1,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
解:(1)∵反比例函数y= 的图象经过点A(-3,2),
∴m=-3×2=-6.
∴反比例函数的解析式为y=
∵点B(1,n)在反比例函数图象上,
∴n=-6.
∴B(1,-6).
把点A,B的坐标分别代入y=kx+b,得
∴一次函数的解析式为y=-2x-4.
-3k+b=2,
k+b=-6.
解得
k=-2,
b=-4.
(2)设直线AB交y轴于点C,则C(0,-4).
∴S△AOB=S△OCA+S△OCB= ×4×3+ ×4×1=8.
23. 环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许值1.0mg/L. 环保局要求该企业立即整改,在15天以内(含15天)排污达标. 整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图S26-8所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度
y与时间x的函数表达式;
(2)该企业所排污水中硫化物的
浓度,能否在15天以内达到标
准?为什么?
解:(1)根据题意,分情况讨论:
①当0≤x≤3时,设线段AB所在直线的表达式为y=kx+b(k≠0).
将点A(0,10),B(3,4)分别代入上式,得
∴y=-2x+10;
②当x>3时,设此时y与x的函数表达式为y= (k≠0).
将点B(3,4)代入上式,得4= 解得k=12. ∴y=
b=10,
3k+b=4.
解得
k=-2,
b=10.
综上所述,整改过程中硫化物的浓度y与时间x的函数表达式为
y=
-2x+10(0≤x≤3),
(x>3).
(2)能.理由如下:
当x=15时,y= =0.8<1,
∴该企业所排污水中硫化物的浓度能在15天以内达到标准.
五、解答题(三)(本大题2小题,每小题10分,共20分)
24. 如图S26-9,一次函数y1=kx+b与反比例函数y2= 的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)P为x轴上一动点,要使PA+PB最小,
试确定点P并求出它的坐标;
(3)利用函数图象直接写出关于x的不等
式 <kx+b的解集.
解:(1)把点A(1,4)代入y2= 得m=4.
∴反比例函数的解析式为y=
把点B(4,n)代入y= ,得n=1.∴B(4,1).
把点A(1,4),B(4,1)分别代入y=kx+b,得
解得
∴一次函数的解析式为y=-x+5.
k+b=4,
4k+b=1.
k=-1,
b=5.
(2)如答图S26-1,作点B关于x轴的对称点B′,则B′
(4,-1),连接AB′交x轴于点P,此时PA+PB=AB′最小.
∴直线AB′的解析式为y=
当y=0时,x= ∴P( 0).
(3)由图像可知,关于x的不等式
<kx+b的解集是x<0或1<x<4.
25. 如图S26-10,已知点A(4,a),B(-10,-4)是一次函数y=kx+b的图象与反比例函数y= 的图象的交点,且一次函数与x轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)连接AO,求△AOB的面积;
(3)在y轴上有一点P,使得S△AOP=
S△AOC,求出点P的坐标.
解:(1)把点B(-10,-4)代入y= 得-4= 解得m=40.
∴反比例函数的解析式为y=
把点A(4,a)代入上式,得a= =10.∴A(4,10).
把点A(4,10),B(-10,-4)分别代入y=kx+b,得
解得
∴一次函数的解析式为y=x+6.
4k+b=10,
-10k+b=-4.
k=1,
b=6.
(2)在y=x+6中,令y=0,求得x=-6,∴C(-6,0).
∴S△AOB=S△AOC+S△BOC= ×6×10+ ×6×4=42.
(3)∵S△AOC= ×6×10=30,S△AOP=S△AOC,
∴ OP·xA=30,即 OP×4=30.
解得OP=15.
∴点P的坐标为(0,15)或(0,-15).
