人教版数学九年级 第二十一章 一元二次方程水平测试课件(共22张PPT)
文档属性
| 名称 | 人教版数学九年级 第二十一章 一元二次方程水平测试课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 14:28:54 | ||
图片预览








文档简介
(共22张PPT)
模拟试卷(活页)
第二十一章 一元二次方程水平测试
(时间:90分钟 满分:120分)
B
C
3. 关于x的方程x2+5x+m=0的一个根为-2,则m的值为( )
A. 6 B. 3 C. -3 D. -6
4. 若方程(a+3)x2+x+9=0是关于x的一元二次方程,则有( )
A.a=3 B.a≠3 C.a=-3 D.a≠-3
A
D
5. 用配方法解方程x2+4x=3,配方正确的是( )
A. (x+2)2=3 B. (x+2)2=4
C. (x+2)2=7 D. (x+1)2=4
6. 方程2x2+3x=3的一次项系数和常数项分别为( )
A. 3和-3 B. 3和3 C. -3和2 D. 3和2
C
A
7. 一元二次方程x2-2x-1=0的根的情况为( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
8. 若关于x的一元二次方程x2-2x+a-1=0没有实数根,则a的取值范围是( )
A. a<2 B. a>2 C. a<-2 D. a>-2
B
B
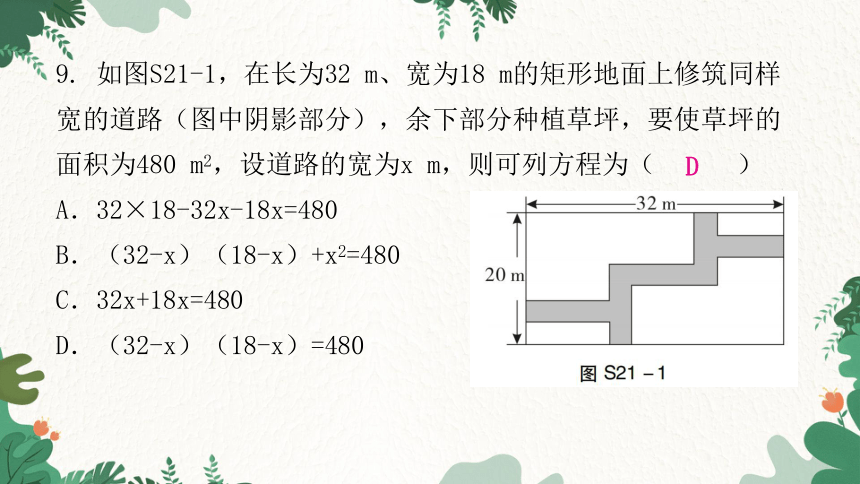
9. 如图S21-1,在长为32 m、宽为18 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为480 m2,设道路的宽为x m,则可列方程为( )
A.32×18-32x-18x=480
B.(32-x)(18-x)+x2=480
C.32x+18x=480
D.(32-x)(18-x)=480
D
10. 一个三角形的两边长分别为3和6,第三边的边长是方程x2-6x+8=0的根,则这个三角形的周长是( )
A. 11 B. 11或13
C. 13 D. 以上选项都不正确
C
二、填空题(本大题7小题,每小题4分,共28分)
11. 方程(x+2)(x-3)=0的根为______________________.
12. 已知x1,x2是方程2x2-3x-1=0的两根,则x1+x2=
__________.
13. 当m=__________时,关于x的一元二次方程x2-2x+m-2=0有两个相等的实数根.
x1=-2,x2=3
3
14. 若m是关于x的方程x2-3x-1=0的解,则代数式6m-2m2+5的值是__________.
15. 若a,b是一元二次方程2x2-x-1=0的两个实数根,则a+ab+b=__________.
16. 一元二次方程x2=6x的解是__________.
17. 参加一次足球联赛的每两队之间都进行两次比赛,共要比赛90场.设共有x个队参加比赛,则依题意可列方程为____________________________.
3
0
x1=0,x2=6
x(x-1)=90
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 解方程:x2-5x+2=0.
解:∵a=1,b=-5,c=2,
∴b2-4ac=(-5)2-4×1×2=17.
∴x=
∴x1= x2=
19.解方程:2x2-4 x=-3.
解:方程可化为2(x2-2 x)=-3.
∴2[x2-2 x+( )2]-4=-3.
∴2(x- )2=1.
∴x- =
∴x1=
20. 解方程:x2-1=6(x-1).
解:方程可化为(x+1)(x-1)=6(x-1).
移项并分解因式,得(x-5)(x-1)=0.
解得x1=5,x2=1.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21. 已知α,β是方程x2-x-1=0的两个实数根,求下列各代数式的值.
(1)α2+β2;
解:由根与系数的关系,得
α+β=1,αβ=-1.
∴α2+β2=(α+β)2-2αβ=1+2=3.
(2)
解:
22. 某小区开展“新农村”建设,今年8月份改造绿化面积为
6 400 m2,到了今年10月份增加到8 100 m2,假设改造绿化面积月平均增长率都相同,求月平均增长率.
解:设月平均增长率为x.
根据题意,得6 400(1+x)2=8 100.
解得x1= =12.5%,x2= (不合题意,舍去).
答:月平均增长率为12.5%.
23. 已知关于x的一元二次方程(m-2)x2-2x+1=0有两个实数根.
(1)求m的取值范围;
(2)在1,2,4三个数中,取一个合适的m值代入方程,并解这个方程.
解:(1)根据题意,得b2-4ac=(-2)2-4(m-2)≥0且m-2≠0.
解得m≤3且m≠2.
∴m的取值范围是m≤3且m≠2.
(2)∵m≤3且m≠2,
∴可取m=1.
当m=1时,原方程化为-x2-2x+1=0.
解得x1=-1- ,x2=-1+ .
五、解答题(三)(本大题2小题,每小题10分,共20分)
24. 已知关于x的一元二次方程x2+2x+k-1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)设两个实数根是x1和x2,且x1+x2-2x1x2=2,求k的值.
解:(1)∵一元二次方程x2+2x+k-1=0有两个不相等的实数根,
∴Δ=b2-4ac=22-4(k-1)>0.
解得k<2.
∴k的取值范围是k<2.
(2)∵一元二次方程x2+2x+k-1=0的两个实数根是x1和x2,
∴x1+x2=-2,x1x2=k-1.
∵x1+x2-2x1x2=2,
∴-2-2(k-1)=2.
∴k=-1.
25. 如图S21-2①,在矩形ABCD中,AB=6 cm,BC=4 cm,动点P从点A出发,以2 cm/s的速度沿AB向点B移动,同时,点Q从点C出发,以1 cm/s的速度沿CD向点D移动(点P到达点B时停止,点Q也随之停止运动),设点P的运动时间为t s.
(1)试求当t为何值时,四边形APQD为矩形;
(2)P,Q两点出发多长时间,线段PQ的长度为5 cm?
解:(1)∵四边形APQD为矩形,
∴AP=DQ.
∴2t=6-t.
解得t=2.
∴当t为2时,四边形APQD为矩形.
(2)如答图S21-1,过点P作PE⊥CD于点E.
∵∠A=∠D=∠DEP=90°,
∴四边形APED是矩形.
∴AP=DE=2t,PE=AD=4.
∴EQ=|DQ-DE|=|6-t-2t|=|6-3t|.
在Rt△PQE中,PE2+EQ2=PQ2,即42+(6-3t)2=52.
解得t1=1,t2=3.
答:当出发1 s或3 s时,线段PQ的长度为5 cm.
模拟试卷(活页)
第二十一章 一元二次方程水平测试
(时间:90分钟 满分:120分)
B
C
3. 关于x的方程x2+5x+m=0的一个根为-2,则m的值为( )
A. 6 B. 3 C. -3 D. -6
4. 若方程(a+3)x2+x+9=0是关于x的一元二次方程,则有( )
A.a=3 B.a≠3 C.a=-3 D.a≠-3
A
D
5. 用配方法解方程x2+4x=3,配方正确的是( )
A. (x+2)2=3 B. (x+2)2=4
C. (x+2)2=7 D. (x+1)2=4
6. 方程2x2+3x=3的一次项系数和常数项分别为( )
A. 3和-3 B. 3和3 C. -3和2 D. 3和2
C
A
7. 一元二次方程x2-2x-1=0的根的情况为( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
8. 若关于x的一元二次方程x2-2x+a-1=0没有实数根,则a的取值范围是( )
A. a<2 B. a>2 C. a<-2 D. a>-2
B
B
9. 如图S21-1,在长为32 m、宽为18 m的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为480 m2,设道路的宽为x m,则可列方程为( )
A.32×18-32x-18x=480
B.(32-x)(18-x)+x2=480
C.32x+18x=480
D.(32-x)(18-x)=480
D
10. 一个三角形的两边长分别为3和6,第三边的边长是方程x2-6x+8=0的根,则这个三角形的周长是( )
A. 11 B. 11或13
C. 13 D. 以上选项都不正确
C
二、填空题(本大题7小题,每小题4分,共28分)
11. 方程(x+2)(x-3)=0的根为______________________.
12. 已知x1,x2是方程2x2-3x-1=0的两根,则x1+x2=
__________.
13. 当m=__________时,关于x的一元二次方程x2-2x+m-2=0有两个相等的实数根.
x1=-2,x2=3
3
14. 若m是关于x的方程x2-3x-1=0的解,则代数式6m-2m2+5的值是__________.
15. 若a,b是一元二次方程2x2-x-1=0的两个实数根,则a+ab+b=__________.
16. 一元二次方程x2=6x的解是__________.
17. 参加一次足球联赛的每两队之间都进行两次比赛,共要比赛90场.设共有x个队参加比赛,则依题意可列方程为____________________________.
3
0
x1=0,x2=6
x(x-1)=90
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 解方程:x2-5x+2=0.
解:∵a=1,b=-5,c=2,
∴b2-4ac=(-5)2-4×1×2=17.
∴x=
∴x1= x2=
19.解方程:2x2-4 x=-3.
解:方程可化为2(x2-2 x)=-3.
∴2[x2-2 x+( )2]-4=-3.
∴2(x- )2=1.
∴x- =
∴x1=
20. 解方程:x2-1=6(x-1).
解:方程可化为(x+1)(x-1)=6(x-1).
移项并分解因式,得(x-5)(x-1)=0.
解得x1=5,x2=1.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21. 已知α,β是方程x2-x-1=0的两个实数根,求下列各代数式的值.
(1)α2+β2;
解:由根与系数的关系,得
α+β=1,αβ=-1.
∴α2+β2=(α+β)2-2αβ=1+2=3.
(2)
解:
22. 某小区开展“新农村”建设,今年8月份改造绿化面积为
6 400 m2,到了今年10月份增加到8 100 m2,假设改造绿化面积月平均增长率都相同,求月平均增长率.
解:设月平均增长率为x.
根据题意,得6 400(1+x)2=8 100.
解得x1= =12.5%,x2= (不合题意,舍去).
答:月平均增长率为12.5%.
23. 已知关于x的一元二次方程(m-2)x2-2x+1=0有两个实数根.
(1)求m的取值范围;
(2)在1,2,4三个数中,取一个合适的m值代入方程,并解这个方程.
解:(1)根据题意,得b2-4ac=(-2)2-4(m-2)≥0且m-2≠0.
解得m≤3且m≠2.
∴m的取值范围是m≤3且m≠2.
(2)∵m≤3且m≠2,
∴可取m=1.
当m=1时,原方程化为-x2-2x+1=0.
解得x1=-1- ,x2=-1+ .
五、解答题(三)(本大题2小题,每小题10分,共20分)
24. 已知关于x的一元二次方程x2+2x+k-1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)设两个实数根是x1和x2,且x1+x2-2x1x2=2,求k的值.
解:(1)∵一元二次方程x2+2x+k-1=0有两个不相等的实数根,
∴Δ=b2-4ac=22-4(k-1)>0.
解得k<2.
∴k的取值范围是k<2.
(2)∵一元二次方程x2+2x+k-1=0的两个实数根是x1和x2,
∴x1+x2=-2,x1x2=k-1.
∵x1+x2-2x1x2=2,
∴-2-2(k-1)=2.
∴k=-1.
25. 如图S21-2①,在矩形ABCD中,AB=6 cm,BC=4 cm,动点P从点A出发,以2 cm/s的速度沿AB向点B移动,同时,点Q从点C出发,以1 cm/s的速度沿CD向点D移动(点P到达点B时停止,点Q也随之停止运动),设点P的运动时间为t s.
(1)试求当t为何值时,四边形APQD为矩形;
(2)P,Q两点出发多长时间,线段PQ的长度为5 cm?
解:(1)∵四边形APQD为矩形,
∴AP=DQ.
∴2t=6-t.
解得t=2.
∴当t为2时,四边形APQD为矩形.
(2)如答图S21-1,过点P作PE⊥CD于点E.
∵∠A=∠D=∠DEP=90°,
∴四边形APED是矩形.
∴AP=DE=2t,PE=AD=4.
∴EQ=|DQ-DE|=|6-t-2t|=|6-3t|.
在Rt△PQE中,PE2+EQ2=PQ2,即42+(6-3t)2=52.
解得t1=1,t2=3.
答:当出发1 s或3 s时,线段PQ的长度为5 cm.
同课章节目录
