河北省唐县2022-2023学年高一下学期5月联考数学试题(含解析)
文档属性
| 名称 | 河北省唐县2022-2023学年高一下学期5月联考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 964.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-22 14:44:08 | ||
图片预览



文档简介
唐县2022-2023学年高一下学期5月联考
数学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:人教A版必修第二册第六章、第七章、第八章、第九章第一节。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数,,则( )
A. B. C. D.
2.的内角A,B,C的对边分别为a,b,c,若,,,则( )
A.2 B. C.3 D.
3.光明社区老年合唱队中,60~70岁的有30人,71~75岁的有15人,76岁及以上的有10人.若用分层抽样的方法抽取n位老人参加某项活动,已知从71~75岁的老人中抽取了3人,则n的值为( )
A.9 B.10 C.11 D.12
4.已知m,n是两条不同的直线,是一个平面,则下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5.某公司用随机数法从公司的500名员工中抽取了20人了解其对烧烤的喜欢程度.先将这500名员工按001,002,…,500进行编号,然后从随机数第3行第3列的数开始向右读,则选出的第7个编号是(注:下面为随机数的第3行和第4行)( )
第3行:7816 6572 0802 6319 8702 4369 9728 0198
第4行:3204 9243 4935 8200 3623 4869 6938 7481
A.492 B.320 C.198 D.280
6.已知向量,,若a与b反向,则向量在向量上的投影向量为( )
A. B. C. D.
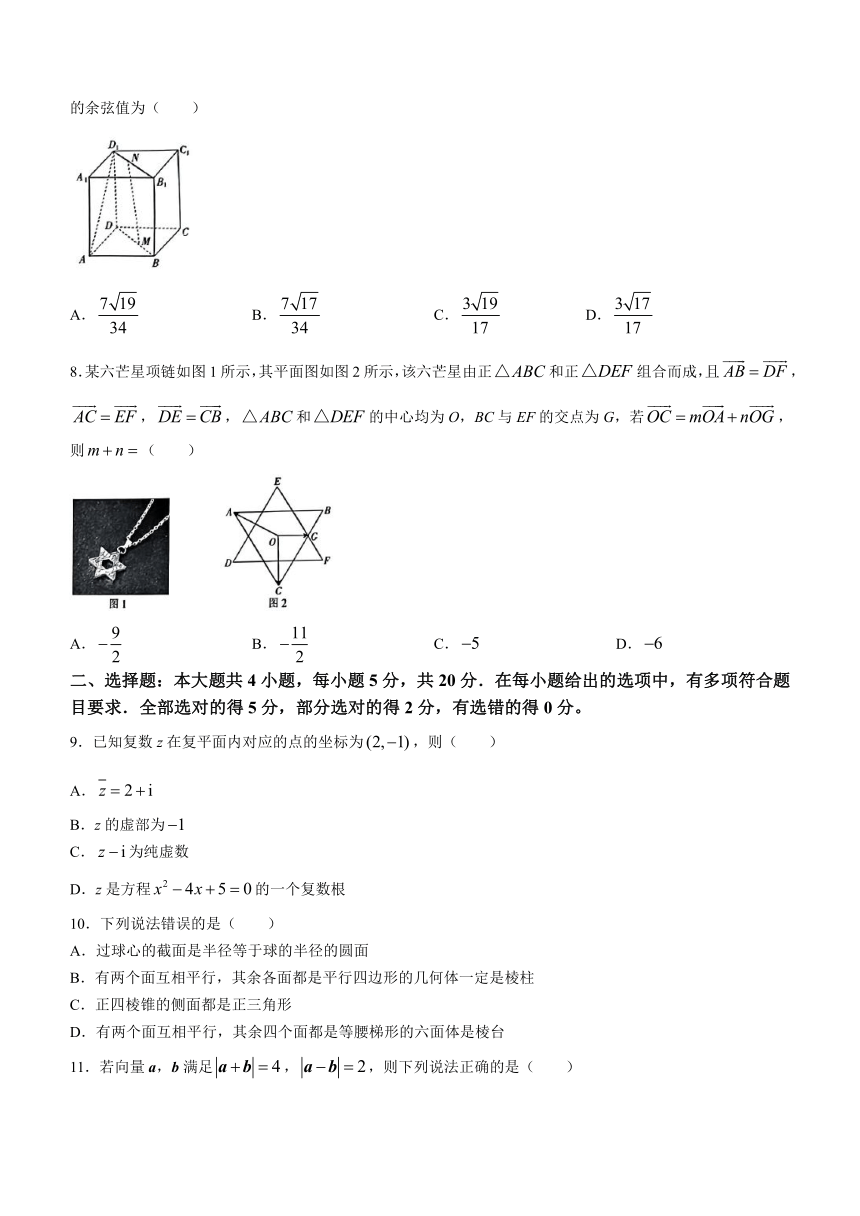
7.在平行六面体中,底面ABCD是菱形,,与底面ABCD垂直,M,N分别在BD和上,且,,,,则异面直线MN与所成角的余弦值为( )
A. B. C. D.
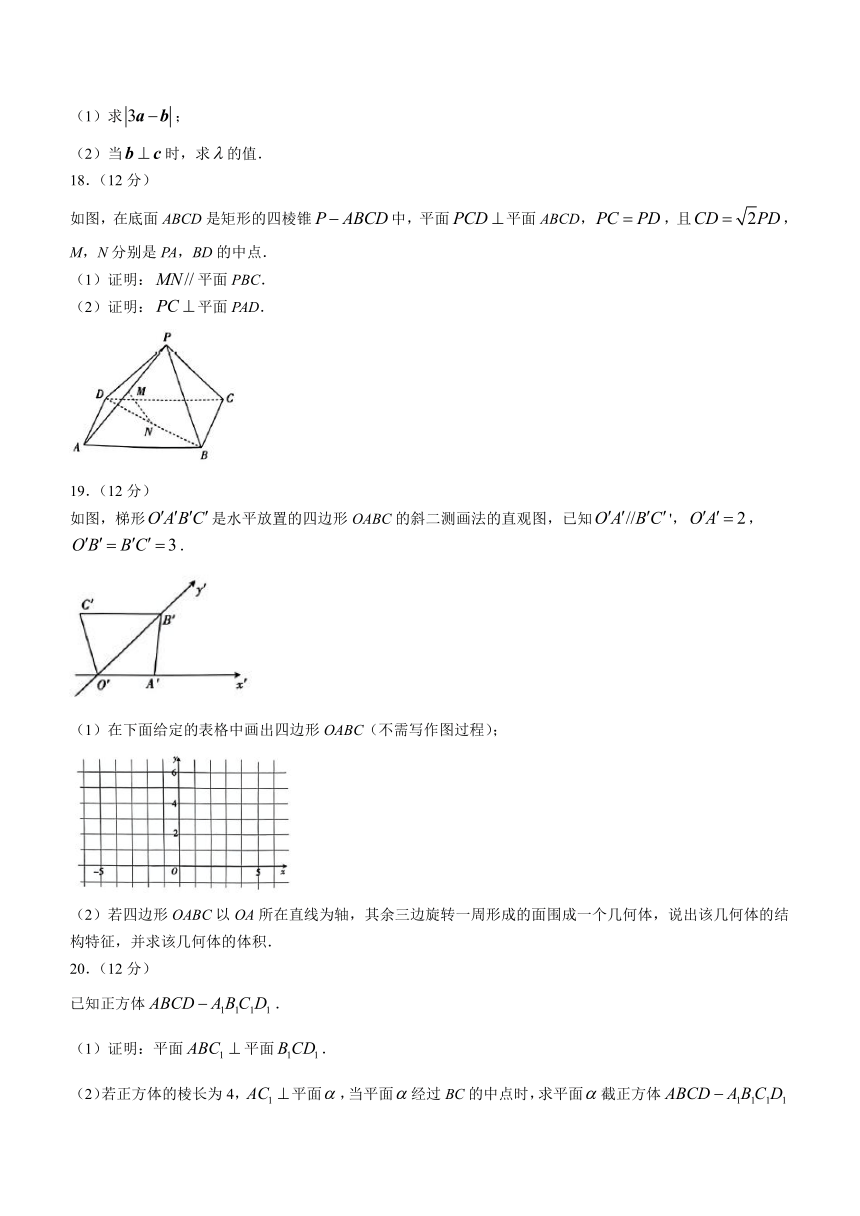
8.某六芒星项链如图1所示,其平面图如图2所示,该六芒星由正和正组合而成,且,,,和的中心均为O,BC与EF的交点为G,若,则( )
A. B. C. D.
二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知复数z在复平面内对应的点的坐标为,则( )
A.
B.z的虚部为
C.为纯虚数
D.z是方程的一个复数根
10.下列说法错误的是( )
A.过球心的截面是半径等于球的半径的圆面
B.有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
C.正四棱锥的侧面都是正三角形
D.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
11.若向量a,b满足,,则下列说法正确的是( )
A.若,则 B.
C.若,则 D.
12.在四棱锥中,底面ABCD,,,,且二面角为,则( )
A.
B.二面角为
C.三棱锥的外接球的表面积为
D.三棱锥的内切球的半径为
三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.某7位小伙伴1分钟的跳绳个数(单位:个)分别为180,182,173,175,a,178,176,已知这7位小伙伴1分钟跳绳个数的平均数为178,则________.
14.某“星舰”可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图所示,其中B,C分别是上、下底面圆的圆心,若米,米,底面圆的直径为9米,则该“星舰”的表面积是________平方米.
15.长度为的线段两个端点到平面的距离分别为和,且这两个端点都在平面的同一侧,则这条线段所在直线与平面所成角的正弦值为________.
16.《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.如图,在鳖臑PABC中,,,,,D,E分别为棱PC,PB上一点,则的最小值为________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知向量a,b的夹角为,且,,.
(1)求;
(2)当时,求的值.
18.(12分)
如图,在底面ABCD是矩形的四棱锥中,平面平面ABCD,,且,M,N分别是PA,BD的中点.
(1)证明:平面PBC.
(2)证明:平面PAD.
19.(12分)
如图,梯形是水平放置的四边形OABC的斜二测画法的直观图,已知',,.
(1)在下面给定的表格中画出四边形OABC(不需写作图过程);
(2)若四边形OABC以OA所在直线为轴,其余三边旋转一周形成的面围成一个几何体,说出该几何体的结构特征,并求该几何体的体积.
20.(12分)
已知正方体.
(1)证明:平面平面.
(2)若正方体的棱长为4,平面,当平面经过BC的中点时,求平面截正方体所得截面的周长.
21.(12分)
的内角A,B,C的对边分别为a,b,c,且.
(1)求C;
(2)若D为AB边上一点,,且,求面积的最小值.
22.(12分)
如图,在斜三棱柱中,E为的中点,M为AB上靠近A的三等分点,N为上靠近的三等分点.
(1)证明:平面平面BEN.
(2)若平面,,与平面的距离为x,,,三棱锥的体积为y,试写出y关于x的函数关系式.
(3)在(2)的条件下,当x为多少时,三棱锥的体积取得最大值?并求出最大值.
唐县2022-2023学年高一下学期5月联考
数学参考答案
1.D .
2.D 由余弦定理得.得.
3.C 由,得.
4.C 若,,则或,A错误;平行于同一平面的两条直线可能平行,可能异面,也可能相交,B错误;若,,则m与不一定垂直,D错误.
5.B 由随机数读法可知,选出的编号依次为166,080,263,198,436,280,320,….所以选出的第7个编号是320.
6.D 由,解得或.当时,a与b同向;当时,a与b反向.所以,向量在向量上的投影向量为.
7.B 如图,在BD上取点E,使得,连接AE,,则,所以与所成的角即与MN所成的角.在中,,,,由余弦定理,,得,在中,,,由余弦定理得.
8.C 如图,连接AG,CE,取AB,CE的交点为H,AG,CE的交点为I,易得O在CE上,H为AB的中点,因为O为的重心,所以.由题意得,则,即,所以,得.
9.ABD 因为,所以,A正确;z的虚部为,B正确;,不是纯虚数,C错误;因为,所以z是方程的一个复数根,D正确.
10.BCD 根据球的特征,A正确;如图1,该几何体不是棱柱,B错误;正四棱锥的侧面都是等腰三角形,不一定是正三角形,C错误;如图2,在正方体中,取AD,BC,,的三等分点,依次连接得到多面体,显然不是棱台,所以D错误.
11.ABD 由题意得得当时,,则,A正确.当时,得或C错误.易得,,由,得(当且仅当时,等号成立),由,得,所以,B正确.易得,由,得,D正确.
12.BCD 因为,,所以为正三角形,取BC的中点E,连接PE,AE,则.因为底面ABCD,所以,又,所以平面PAE,则,则为二面角的平面角,所以,所以.因为,,,所以由余弦定理得,则,A错误.因为,所以,可证,所以即二面角的平面角,因为,所以,B正确,设O为三棱锥外接球的球心,取的中心F,连接OF,OA,则,且,OA为三棱锥外接球的半径.因为,所以三棱锥的外接球的表面积为,C正确.设三棱锥的内切球的半径为r,则根据等体积法可得,解得,D正确.
13.182 由条件可知,解得.
14. 依题意可得,该“星舰”的表面积是平方米.
15. 设长度为的线段为AB,A,B在平面内的射影分别为D,C,延长BA与平面交于M,则是AB与平面所成的角,作交BC于N,则,如图所示,,,.
16. 因为,所以,设,,则.
设,,因为,所以,
所以,则,.
将沿着PB转动到P,A,B,C四点共面,如图所示,此时,,
过A作于H,则的最小值为.
17.解:(1)由, 4分
得. 5分
(2)由题设得, 8分
则, 9分
解得. 10分
18.证明:(1)连接AC,因为ABCD是矩形,N是BD的中点,
所以N是AC的中点. 2分
因为M是PA的中点,所以, 4分
又平面PBC,平面PBC,所以平面PBC. 6分
(2)因为,且,所以, 8分
因为平面平面ABCD,平面平面,
,所以平面, 10分
因为平面PCD,所以,
又,所以平面PAD. 12分
19.解:(1)画出四边形OABC,如下图所示:
5分
(2)该几何体是一个组合体,由两部分组成,一部分是以OA为高,O为底面圆心且OB为半径的圆锥,另一部分可看作是一个以BC为高,OB为半径的圆柱挖去一个同底等高的圆锥得到的几何体. 8分
该几何体的体积为. 12分
【注】第(1)问中,,,,只要这三条线段的长度正确,所画的四边形如图所示即可得分,未标注字母A,B,C扣1分,若绘制的图中,,则得0分.
20.(1)证明:在正方体中,平面,
因为平面,所以. 1分
在正方形中,,又,
所以平面. 3分
因为平面,所以平面平面. 4分
(2)解:因为平面,平面,
所以. 5分
在正方形中,,
又,所以平面, 6分
因为平面,所以. 7分
由(1)知平面,则.
又,所以平面BCD, 8分
因为平面,所以平面平面. 9分
分别取BC,CD,,,,的中点E,F,G,H,M,N,连接各点,则多边形EFGHMN即平面截正方体所得的截面. 10分
又,所以平面截正方体所得的截面的周长为. 12分
21.解:(1)(方法一)由余弦定理得,
得,即, 3分
则, 4分
即. 5分
(方法二)由正弦定理得,得. 3分
因为,所以,则, 4分
即. 5分
(2)在中,由正弦定理得,
在中,由正弦定理得.
由题意得. 7分
因为,所以,得,
得,即CD为C的角平分线. 8分
由,得, 9分
得,所以 10分
当且仅当时,等号成立. 11分
故的面积为,即面积的最小值为. 12分
22.(1)证明:在斜三棱柱中,四边形是平行四边形,且M为AB上靠近A的三等分点,N为上靠近的三等分点,
所以且,所以四边形为平行四边形,所以. 1分
因为平面BEN,平面BEN,所以平面BEN. 2分
取上靠近的三等分点F,连接,FM,如图所示,
则,易得四边形为平行四边形,所以, 3分
则,又平面BEN,平面BEN,所以平面BEN. 4分
因为,,平面,所以平面平面BEN. 5分
(2)解:因为平面,所以,且,
所以,所以. 6分
因为,所以平面,
则.又因为,,所以上平面BEN,则, 7分
记与BN的交点为Q,
因为,且,,,
所以,,
则, 9分
所以,
即. 10分
(3)解:由(2)得,令,
当,即时,,此时, 11分
故当时,三棱锥的体积取得最大值,且最大值为16. 12分
数学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:人教A版必修第二册第六章、第七章、第八章、第九章第一节。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数,,则( )
A. B. C. D.
2.的内角A,B,C的对边分别为a,b,c,若,,,则( )
A.2 B. C.3 D.
3.光明社区老年合唱队中,60~70岁的有30人,71~75岁的有15人,76岁及以上的有10人.若用分层抽样的方法抽取n位老人参加某项活动,已知从71~75岁的老人中抽取了3人,则n的值为( )
A.9 B.10 C.11 D.12
4.已知m,n是两条不同的直线,是一个平面,则下列说法正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5.某公司用随机数法从公司的500名员工中抽取了20人了解其对烧烤的喜欢程度.先将这500名员工按001,002,…,500进行编号,然后从随机数第3行第3列的数开始向右读,则选出的第7个编号是(注:下面为随机数的第3行和第4行)( )
第3行:7816 6572 0802 6319 8702 4369 9728 0198
第4行:3204 9243 4935 8200 3623 4869 6938 7481
A.492 B.320 C.198 D.280
6.已知向量,,若a与b反向,则向量在向量上的投影向量为( )
A. B. C. D.
7.在平行六面体中,底面ABCD是菱形,,与底面ABCD垂直,M,N分别在BD和上,且,,,,则异面直线MN与所成角的余弦值为( )
A. B. C. D.
8.某六芒星项链如图1所示,其平面图如图2所示,该六芒星由正和正组合而成,且,,,和的中心均为O,BC与EF的交点为G,若,则( )
A. B. C. D.
二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知复数z在复平面内对应的点的坐标为,则( )
A.
B.z的虚部为
C.为纯虚数
D.z是方程的一个复数根
10.下列说法错误的是( )
A.过球心的截面是半径等于球的半径的圆面
B.有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
C.正四棱锥的侧面都是正三角形
D.有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台
11.若向量a,b满足,,则下列说法正确的是( )
A.若,则 B.
C.若,则 D.
12.在四棱锥中,底面ABCD,,,,且二面角为,则( )
A.
B.二面角为
C.三棱锥的外接球的表面积为
D.三棱锥的内切球的半径为
三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.某7位小伙伴1分钟的跳绳个数(单位:个)分别为180,182,173,175,a,178,176,已知这7位小伙伴1分钟跳绳个数的平均数为178,则________.
14.某“星舰”可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图所示,其中B,C分别是上、下底面圆的圆心,若米,米,底面圆的直径为9米,则该“星舰”的表面积是________平方米.
15.长度为的线段两个端点到平面的距离分别为和,且这两个端点都在平面的同一侧,则这条线段所在直线与平面所成角的正弦值为________.
16.《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.如图,在鳖臑PABC中,,,,,D,E分别为棱PC,PB上一点,则的最小值为________.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知向量a,b的夹角为,且,,.
(1)求;
(2)当时,求的值.
18.(12分)
如图,在底面ABCD是矩形的四棱锥中,平面平面ABCD,,且,M,N分别是PA,BD的中点.
(1)证明:平面PBC.
(2)证明:平面PAD.
19.(12分)
如图,梯形是水平放置的四边形OABC的斜二测画法的直观图,已知',,.
(1)在下面给定的表格中画出四边形OABC(不需写作图过程);
(2)若四边形OABC以OA所在直线为轴,其余三边旋转一周形成的面围成一个几何体,说出该几何体的结构特征,并求该几何体的体积.
20.(12分)
已知正方体.
(1)证明:平面平面.
(2)若正方体的棱长为4,平面,当平面经过BC的中点时,求平面截正方体所得截面的周长.
21.(12分)
的内角A,B,C的对边分别为a,b,c,且.
(1)求C;
(2)若D为AB边上一点,,且,求面积的最小值.
22.(12分)
如图,在斜三棱柱中,E为的中点,M为AB上靠近A的三等分点,N为上靠近的三等分点.
(1)证明:平面平面BEN.
(2)若平面,,与平面的距离为x,,,三棱锥的体积为y,试写出y关于x的函数关系式.
(3)在(2)的条件下,当x为多少时,三棱锥的体积取得最大值?并求出最大值.
唐县2022-2023学年高一下学期5月联考
数学参考答案
1.D .
2.D 由余弦定理得.得.
3.C 由,得.
4.C 若,,则或,A错误;平行于同一平面的两条直线可能平行,可能异面,也可能相交,B错误;若,,则m与不一定垂直,D错误.
5.B 由随机数读法可知,选出的编号依次为166,080,263,198,436,280,320,….所以选出的第7个编号是320.
6.D 由,解得或.当时,a与b同向;当时,a与b反向.所以,向量在向量上的投影向量为.
7.B 如图,在BD上取点E,使得,连接AE,,则,所以与所成的角即与MN所成的角.在中,,,,由余弦定理,,得,在中,,,由余弦定理得.
8.C 如图,连接AG,CE,取AB,CE的交点为H,AG,CE的交点为I,易得O在CE上,H为AB的中点,因为O为的重心,所以.由题意得,则,即,所以,得.
9.ABD 因为,所以,A正确;z的虚部为,B正确;,不是纯虚数,C错误;因为,所以z是方程的一个复数根,D正确.
10.BCD 根据球的特征,A正确;如图1,该几何体不是棱柱,B错误;正四棱锥的侧面都是等腰三角形,不一定是正三角形,C错误;如图2,在正方体中,取AD,BC,,的三等分点,依次连接得到多面体,显然不是棱台,所以D错误.
11.ABD 由题意得得当时,,则,A正确.当时,得或C错误.易得,,由,得(当且仅当时,等号成立),由,得,所以,B正确.易得,由,得,D正确.
12.BCD 因为,,所以为正三角形,取BC的中点E,连接PE,AE,则.因为底面ABCD,所以,又,所以平面PAE,则,则为二面角的平面角,所以,所以.因为,,,所以由余弦定理得,则,A错误.因为,所以,可证,所以即二面角的平面角,因为,所以,B正确,设O为三棱锥外接球的球心,取的中心F,连接OF,OA,则,且,OA为三棱锥外接球的半径.因为,所以三棱锥的外接球的表面积为,C正确.设三棱锥的内切球的半径为r,则根据等体积法可得,解得,D正确.
13.182 由条件可知,解得.
14. 依题意可得,该“星舰”的表面积是平方米.
15. 设长度为的线段为AB,A,B在平面内的射影分别为D,C,延长BA与平面交于M,则是AB与平面所成的角,作交BC于N,则,如图所示,,,.
16. 因为,所以,设,,则.
设,,因为,所以,
所以,则,.
将沿着PB转动到P,A,B,C四点共面,如图所示,此时,,
过A作于H,则的最小值为.
17.解:(1)由, 4分
得. 5分
(2)由题设得, 8分
则, 9分
解得. 10分
18.证明:(1)连接AC,因为ABCD是矩形,N是BD的中点,
所以N是AC的中点. 2分
因为M是PA的中点,所以, 4分
又平面PBC,平面PBC,所以平面PBC. 6分
(2)因为,且,所以, 8分
因为平面平面ABCD,平面平面,
,所以平面, 10分
因为平面PCD,所以,
又,所以平面PAD. 12分
19.解:(1)画出四边形OABC,如下图所示:
5分
(2)该几何体是一个组合体,由两部分组成,一部分是以OA为高,O为底面圆心且OB为半径的圆锥,另一部分可看作是一个以BC为高,OB为半径的圆柱挖去一个同底等高的圆锥得到的几何体. 8分
该几何体的体积为. 12分
【注】第(1)问中,,,,只要这三条线段的长度正确,所画的四边形如图所示即可得分,未标注字母A,B,C扣1分,若绘制的图中,,则得0分.
20.(1)证明:在正方体中,平面,
因为平面,所以. 1分
在正方形中,,又,
所以平面. 3分
因为平面,所以平面平面. 4分
(2)解:因为平面,平面,
所以. 5分
在正方形中,,
又,所以平面, 6分
因为平面,所以. 7分
由(1)知平面,则.
又,所以平面BCD, 8分
因为平面,所以平面平面. 9分
分别取BC,CD,,,,的中点E,F,G,H,M,N,连接各点,则多边形EFGHMN即平面截正方体所得的截面. 10分
又,所以平面截正方体所得的截面的周长为. 12分
21.解:(1)(方法一)由余弦定理得,
得,即, 3分
则, 4分
即. 5分
(方法二)由正弦定理得,得. 3分
因为,所以,则, 4分
即. 5分
(2)在中,由正弦定理得,
在中,由正弦定理得.
由题意得. 7分
因为,所以,得,
得,即CD为C的角平分线. 8分
由,得, 9分
得,所以 10分
当且仅当时,等号成立. 11分
故的面积为,即面积的最小值为. 12分
22.(1)证明:在斜三棱柱中,四边形是平行四边形,且M为AB上靠近A的三等分点,N为上靠近的三等分点,
所以且,所以四边形为平行四边形,所以. 1分
因为平面BEN,平面BEN,所以平面BEN. 2分
取上靠近的三等分点F,连接,FM,如图所示,
则,易得四边形为平行四边形,所以, 3分
则,又平面BEN,平面BEN,所以平面BEN. 4分
因为,,平面,所以平面平面BEN. 5分
(2)解:因为平面,所以,且,
所以,所以. 6分
因为,所以平面,
则.又因为,,所以上平面BEN,则, 7分
记与BN的交点为Q,
因为,且,,,
所以,,
则, 9分
所以,
即. 10分
(3)解:由(2)得,令,
当,即时,,此时, 11分
故当时,三棱锥的体积取得最大值,且最大值为16. 12分
同课章节目录
