平方差公式[上学期]
图片预览


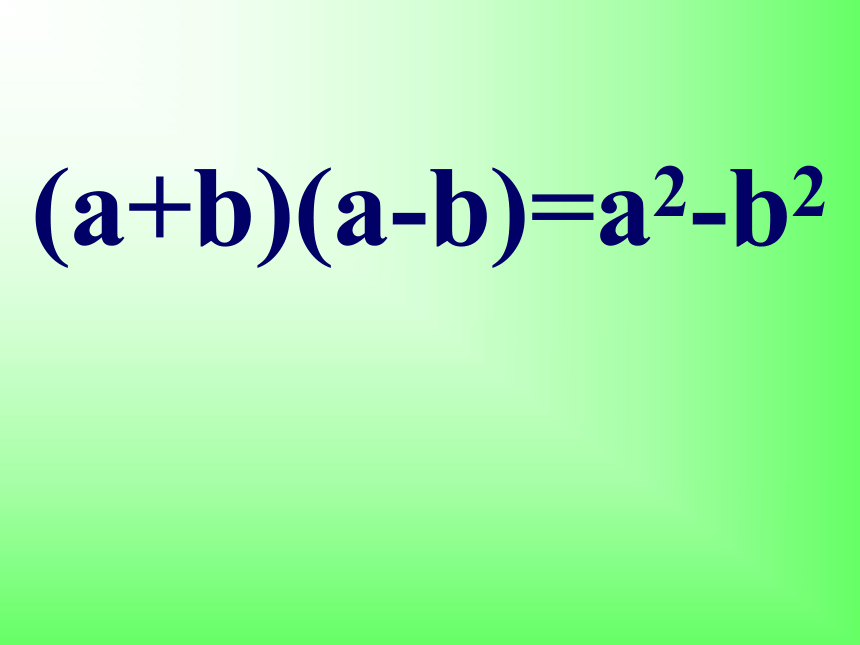



文档简介
课件13张PPT。
13.31 平方差公式(1) 一块长方形花坛,长(a+b)米,宽(a-b)米,它的面积是多少?计算:(a+b)(a-b)=?a2-b2(a+b)(a-b)=a2-b2
(a+b)(a-b)=a2-b2
a与 b的和乘以 a 与 b 的 差
等 于 a、b的平方差 例1 计算: (a+b)(a-b)=a2-b2 (1)(a+3)(a-3); (2)(2a+3b)(2a-3b); (3)(1+2c)(1-2c)
解 (1)(a+3)(a-3)
=a2-32 =a2-9
(2)(2a+3b)(2a-3b)
=(2a)2-(3b)2
=4a2-9b2
(3)(1+2c)(1-2c)
=12-(2c)2 =1-4c2练习计算(1) (a+3)(a-3)
(2) (2a+3b)(2a-3b)
(3)(1+2c)(1-2c)
变式训练
(1)(-2x2+ )(-2x2- )
(2)(3a-b)(-b-3a)
(3)(-2x-y)(2x-y)
(a+b)(a-b)=a2-b2 平方差公式的八种变形:
(b+a)(-b+a)
(-a-b)(a-b)
( 0.5a+3b)(0.5a-3b)
(a2+b2)(a2-b2)
(a-b-c)(a-b+c)
(a+b)(a-b)(-a-b)(-a+b)
(a-b)(a+b)(a2+b2)(a4+b4)
(a-b+c-d2)-(a+b-c+d2)位置变化符号变化系数变化指数变化增项变化增因式变化连用公式变化逆用公式变化 (a+b)(a-b)=(a)2-(b)2
课堂练习 1、 (200+5) (200-5)
变式:200.5×199.5
60.5×59.5
2、 (1+3b) (1-3b)
3、 (4a+3) (4a-3)
4、 (3x+2y2) (3x-2y2)
5、 [(x+y)+z] [(x+y)-z]
7、(-a-b)(a+b)
8、[x+(y+1)] [x-(y+1)]
9、(a+b+c) (a+b-c)
10、(a+b+c) (a-b+c) !
? 11、(x+3) (x-3) (x2+9) (x4+81)(a+b)(a-b)=(a)2-(b)2 a2-b2=(a+b)(a-b) 逆向思维训练:
11、( )( )=n2-m2
12、 ( ) ( ) =4x2-9y2
13、(5+a)( ) =25-a2
提高训练(2+1)(22+1)(24+1)(28+1)(216+1)
(2a-1)(2a+1)(4a2+1)(16a4+1)
(x-3)(x+3)(x2+9)(x4+81)
(a+b)(a-b)=(a)2-(b)2相反为b 小结 相同为a 适当交换合理加括平方差公式的结构特征:(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数。(2)相同项的平方减去相反项的平方。(a+b)(a-b)=a2-b2
13.31 平方差公式(1) 一块长方形花坛,长(a+b)米,宽(a-b)米,它的面积是多少?计算:(a+b)(a-b)=?a2-b2(a+b)(a-b)=a2-b2
(a+b)(a-b)=a2-b2
a与 b的和乘以 a 与 b 的 差
等 于 a、b的平方差 例1 计算: (a+b)(a-b)=a2-b2 (1)(a+3)(a-3); (2)(2a+3b)(2a-3b); (3)(1+2c)(1-2c)
解 (1)(a+3)(a-3)
=a2-32 =a2-9
(2)(2a+3b)(2a-3b)
=(2a)2-(3b)2
=4a2-9b2
(3)(1+2c)(1-2c)
=12-(2c)2 =1-4c2练习计算(1) (a+3)(a-3)
(2) (2a+3b)(2a-3b)
(3)(1+2c)(1-2c)
变式训练
(1)(-2x2+ )(-2x2- )
(2)(3a-b)(-b-3a)
(3)(-2x-y)(2x-y)
(a+b)(a-b)=a2-b2 平方差公式的八种变形:
(b+a)(-b+a)
(-a-b)(a-b)
( 0.5a+3b)(0.5a-3b)
(a2+b2)(a2-b2)
(a-b-c)(a-b+c)
(a+b)(a-b)(-a-b)(-a+b)
(a-b)(a+b)(a2+b2)(a4+b4)
(a-b+c-d2)-(a+b-c+d2)位置变化符号变化系数变化指数变化增项变化增因式变化连用公式变化逆用公式变化 (a+b)(a-b)=(a)2-(b)2
课堂练习 1、 (200+5) (200-5)
变式:200.5×199.5
60.5×59.5
2、 (1+3b) (1-3b)
3、 (4a+3) (4a-3)
4、 (3x+2y2) (3x-2y2)
5、 [(x+y)+z] [(x+y)-z]
7、(-a-b)(a+b)
8、[x+(y+1)] [x-(y+1)]
9、(a+b+c) (a+b-c)
10、(a+b+c) (a-b+c) !
? 11、(x+3) (x-3) (x2+9) (x4+81)(a+b)(a-b)=(a)2-(b)2 a2-b2=(a+b)(a-b) 逆向思维训练:
11、( )( )=n2-m2
12、 ( ) ( ) =4x2-9y2
13、(5+a)( ) =25-a2
提高训练(2+1)(22+1)(24+1)(28+1)(216+1)
(2a-1)(2a+1)(4a2+1)(16a4+1)
(x-3)(x+3)(x2+9)(x4+81)
(a+b)(a-b)=(a)2-(b)2相反为b 小结 相同为a 适当交换合理加括平方差公式的结构特征:(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数。(2)相同项的平方减去相反项的平方。(a+b)(a-b)=a2-b2
