湖南省永州市名校2022-2023学年高一下学期6月月考数学试题(含解析)
文档属性
| 名称 | 湖南省永州市名校2022-2023学年高一下学期6月月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-22 14:59:35 | ||
图片预览




文档简介
永州市名校2022-2023学年高一下学期6月月考
数学卷
考试时间:120分钟
注意事项:
一、单选题
1.己知复数,,则( )
A. B.6 C. D.
2.已知点G是三角形所在平面内一点,满足,则G点是三角形的( )
A.垂心 B.内心 C.外心 D.重心
3.已知m,n表示两条不同的直线,表示平面.下列说法正确的是( )
A.若,,则
B.若,,则
C.若,,则
D.若,,则
4.在中,角的对边分别为.若,,,则的值为( )
A.1 B. C. D.
5.在中,若,,则的外接圆的半径为( )
A. B. C. D.
6.已知正方形的边长为1,点是对角线上任意一点,则的取值范围为( )
A. B. C. D.
7.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式(e是自然对数的底,i是虚数单位),这个公式在复变论中占有非常重要的地位,被普为“数学中的天桥”.下列说法正确的是( )
A. B.
C. D.
8.己知向量,,其中,若平面向量满足,且,则的取值范围是( )
A. B. C. D.
二、多选题
9.如图,D,E,F分别是的边,,的中点,则等于( )
A. B. C. D.
10.下列命题中错误的是( )
A.若复数满足,则
B.若复数,满足,则
C.若复数,则z为纯虚数的充要条件是
D.若复数,则
11. 的内角A,B,C的对边分别为a,b,c,且,,若边的中线,则下列结论正确的有( )
A. B.
C. D.的面积为
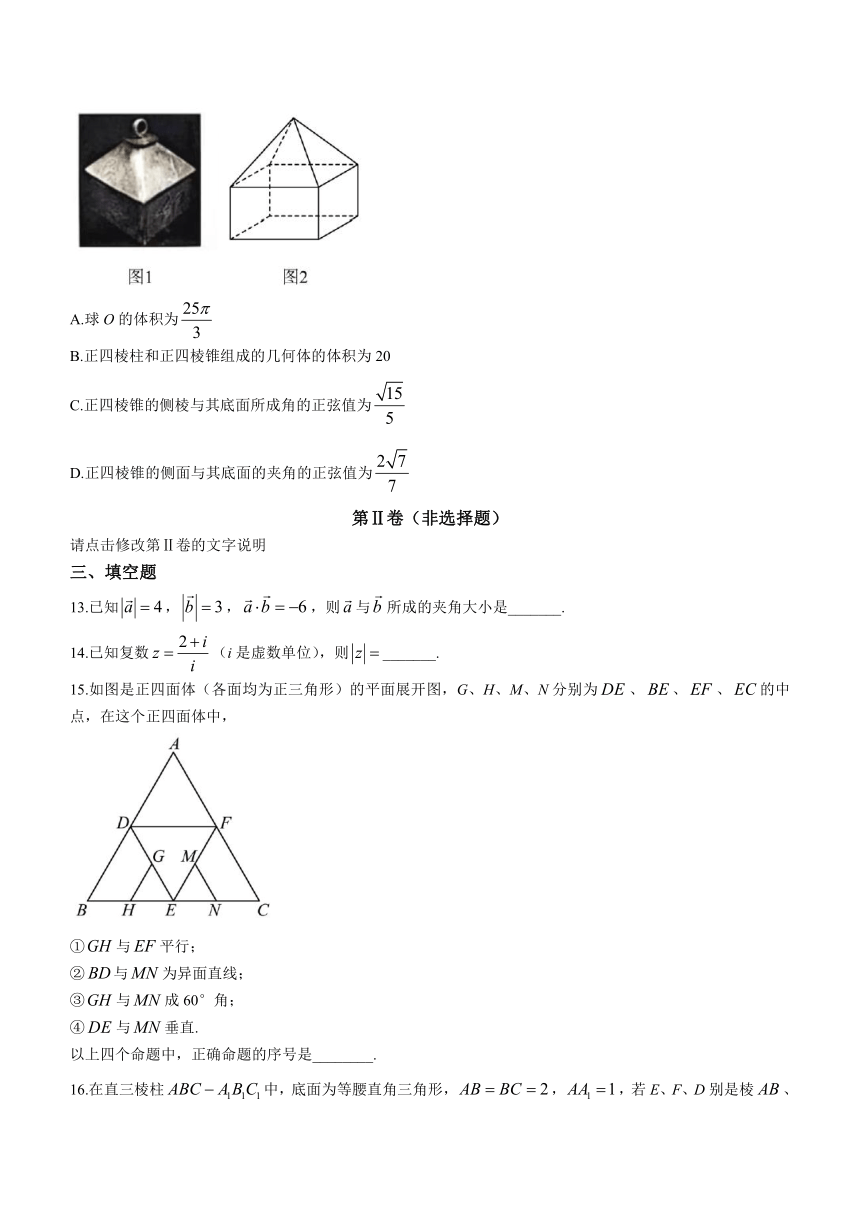
12.我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,本是官员或私人签署文件时代表身份的信物,后因其独特的文化内涵,也被作为装饰物来使用.图1是明清时期的一个金属印章摆件,除去顶部的环可以看作是一个正四棱柱和一个正四棱锥组成的几何体;如图2,已知正四棱柱和正四棱锥的高之比为,且底面边长均为,若该几何体的所有顶点都在球O的表面上,则( )
A.球O的体积为
B.正四棱柱和正四棱锥组成的几何体的体积为20
C.正四棱锥的侧棱与其底面所成角的正弦值为
D.正四棱锥的侧面与其底面的夹角的正弦值为
第Ⅱ卷(非选择题)
请点击修改第Ⅱ卷的文字说明
三、填空题
13.已知,,,则与所成的夹角大小是_______.
14.已知复数(i是虚数单位),则_______.
15.如图是正四面体(各面均为正三角形)的平面展开图,G、H、M、N分别为、、、的中点,在这个正四面体中,
①与平行;
②与为异面直线;
③与成60°角;
④与垂直.
以上四个命题中,正确命题的序号是________.
16.在直三棱柱中,底面为等腰直角三角形,,,若E、F、D别是棱、、的中点,则下列四个命题:
①;
②三棱锥的外接球的表面积为;
③三棱锥的体积为;
④直线与平面所成角为,
其中正确的命题有________.(把所有正确命题的序号填在横线上)
四、解答题
17.已知,,与的夹角为60°.
(1)求:,;(2)求:.
18.已知,,方程的一个根为,复数,满足.
(1)求复数;
(2)若,求复数
19.如图,在三棱柱中,侧面是正方形,M,N分别是,的中点,平面 .
(1)求证:平面平面;
(2)求证:平面;
(3)若三棱柱的体积为10,求三棱锥的体积.
20.在中,,,.
(1)求的长;
(2)求的值.
21.如图,某巡逻艇在A处发现北偏东30°相距海里的B处有一艘走私船,正沿东偏南45°的方向以3海里/小时的速度向我海岸行驶,巡逻艇立即以海里/小时的速度沿着正东方向直线追去,1小时后,巡逻艇到达C处,走私船到达D处,此时走私船发现了巡逻艇,立即改变航向,以原速向正东方向逃窜,巡逻艇立即加速以海里/小时的速度沿着直线追击
(1)当走私船发现了巡逻艇时,两船相距多少海里
(2)问巡逻艇应该沿什么方向去追,才能最快追上走私船
22.如图,在平行四边形中,,,E为的中点,以为折痕将折起,使点D到达点P的位置,且,F,G分别为,的中点.
(1)证明:平面 .
(2)若平面与平面的交线为,求直线与平面所成角的正弦值.
永州市名校2022-2023学年高一下学期6月月考
数学答案
一、单选题(每题5分)
1.B. 2.D 3. D 4.A.5. B
6.C.【详解】设,则,,
,所以,
又,所以,又,
所以.
7. C
【详解】对于A,当时,因为,所以,故不一定成立,选项A错误;
对于B,,所以B错误;
对于C,由,,所以,得出,选项C正确;
对于D,由C选项的分析得,得出,选项D错误.
8. A
【详解】设,
则由可得, ,
两式相加得: ,故,由于,,故 ,
所以由得, ,即,由可得,
二、多选题(每题5分)
9. BCD 10. ABC
当时,即,,,则成立,D正确.
11. ACD
【详解】根据正弦定理,由
,
因为,所以,因此,
因为,所以,因此选项A正确,选项B不正确;
因为是中线,所以由
,或舍去,
因此,所以选项C正确;
△ABC的面积为,所以选项D正确,
12.BD
【详解】设正四棱锥为,其底面中心为;
设正四棱柱为,其下底面中心为,
设是的中点,连接,
是球的球心,设球的半径为,
设正四棱柱的高为,则正四棱锥的高为,为正数,
所以,,
所以,所以,解得,
所以,球的体积,A选项错误.
组合体的体积为,B选项正确.
依题意可知正四棱锥的侧棱与其底面所成角为,
,C选项错误.
根据正四棱锥的性质可知:,
所以是正四棱锥的侧面与其底面的夹角,
,D选项正确.
三、填空题(每题5分)
13. //120°
14.
15.②③④
【详解】还原成正四面体知GH与EF为异面直线,
BD与MN为异面直线,GH与MN成60°角,
因为正四面体对棱垂直,所以,所以DE⊥MN.
16.①②③
【详解】
对于①,取中点,连接,
∵为中点,,,∴四边形为正方形,则
在中,,分别为,的中点,则∥,且
∵为的中点,且∥,∴∥且
∴四边形为平行四边形,∴∥
∴,故①正确;
对于②,∵,,∴
∵面,
∴三棱锥的外接球的球心在线段的中点处,则外接球的半径为
∴三棱锥的外接球的表面积为,故②正确;
对于③,∵,,,
在中,,,,
同理可得,则三棱锥为正四面体,
所以该正四面体的高,底面面积,
体积,故③正确;
对于④,∵面,∴直线在平面上的投影为直线
则为直线与平面所成的角
在中,
∴直线与平面所成的角不是,故④不正确.
故答案为:①②③.
四、解答题(17题10分,18-22每题12分)
17.由得
又
18.(1)依题意,得,即,
由复数相等的定义及a,,得,解得.
故复数.
(2)设(,),由,得,
,
又,得,即,所以,
解得,所以.
19.(1)∵平面,平面,∴,
在正方形中,,∵,∴平面.
∵平面,∴平面平面.
(2)设中点为,连接,∵分别是的中点,
∴,且.又点是的中点,∴.
∵,且,∴,且,
∴四边形是平行四边形,∴.
∵平面,平面, ∴平面.
(3)连接,则,∵为的中点,
∴三棱锥的体积.
20.(1)在中,,由正弦定理得
(2)∵,
因为,所以 ,
∴,,
.
21.(1)由题意知,当走私船发现了巡逻艇时,走私船在D处,巡逻艇在C处,此时,由题意知
在中,由余弦定理得
所以
在中, 由正弦定理得,即
所以(舍去)
所在又
在中,
由余弦定理得
, 故当走私船发现了巡逻艇时,两船相距海里.
(2)当巡逻艇经过小时经方向在处追上走私船,
则
在中,由正弦定理得:
则
所以,
在中,由正弦定理得:
则,故 (舍)
故巡逻艇应该北偏东方向去追,才能最快追上走私船.
22.(1)
连接,交于,并连接,
由、分别是、的中点,而,故为正方形,
所以为的中点,又是的中点,
所以,而面,面,故面.
(2)
由题易知:且均为等腰三角形,且均为等边三角形,
若为中点,连接,则,
而,面,则面,
又面,故面面,面面,
所以在面上的射影在直线上,
过作直线,而,则,故直线为面与面的交线,
所以直线与平面所成角,即为与面所成角,
由题设,,,令,则,,
因为面,面,故,
所以,又,易知,
在△中,,整理得,
所以,故,,
若到面的距离为,且,即,
所以,,,,
综上,,则.
数学卷
考试时间:120分钟
注意事项:
一、单选题
1.己知复数,,则( )
A. B.6 C. D.
2.已知点G是三角形所在平面内一点,满足,则G点是三角形的( )
A.垂心 B.内心 C.外心 D.重心
3.已知m,n表示两条不同的直线,表示平面.下列说法正确的是( )
A.若,,则
B.若,,则
C.若,,则
D.若,,则
4.在中,角的对边分别为.若,,,则的值为( )
A.1 B. C. D.
5.在中,若,,则的外接圆的半径为( )
A. B. C. D.
6.已知正方形的边长为1,点是对角线上任意一点,则的取值范围为( )
A. B. C. D.
7.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式(e是自然对数的底,i是虚数单位),这个公式在复变论中占有非常重要的地位,被普为“数学中的天桥”.下列说法正确的是( )
A. B.
C. D.
8.己知向量,,其中,若平面向量满足,且,则的取值范围是( )
A. B. C. D.
二、多选题
9.如图,D,E,F分别是的边,,的中点,则等于( )
A. B. C. D.
10.下列命题中错误的是( )
A.若复数满足,则
B.若复数,满足,则
C.若复数,则z为纯虚数的充要条件是
D.若复数,则
11. 的内角A,B,C的对边分别为a,b,c,且,,若边的中线,则下列结论正确的有( )
A. B.
C. D.的面积为
12.我国有着丰富悠久的“印章文化”,古时候的印章一般用贵重的金属或玉石制成,本是官员或私人签署文件时代表身份的信物,后因其独特的文化内涵,也被作为装饰物来使用.图1是明清时期的一个金属印章摆件,除去顶部的环可以看作是一个正四棱柱和一个正四棱锥组成的几何体;如图2,已知正四棱柱和正四棱锥的高之比为,且底面边长均为,若该几何体的所有顶点都在球O的表面上,则( )
A.球O的体积为
B.正四棱柱和正四棱锥组成的几何体的体积为20
C.正四棱锥的侧棱与其底面所成角的正弦值为
D.正四棱锥的侧面与其底面的夹角的正弦值为
第Ⅱ卷(非选择题)
请点击修改第Ⅱ卷的文字说明
三、填空题
13.已知,,,则与所成的夹角大小是_______.
14.已知复数(i是虚数单位),则_______.
15.如图是正四面体(各面均为正三角形)的平面展开图,G、H、M、N分别为、、、的中点,在这个正四面体中,
①与平行;
②与为异面直线;
③与成60°角;
④与垂直.
以上四个命题中,正确命题的序号是________.
16.在直三棱柱中,底面为等腰直角三角形,,,若E、F、D别是棱、、的中点,则下列四个命题:
①;
②三棱锥的外接球的表面积为;
③三棱锥的体积为;
④直线与平面所成角为,
其中正确的命题有________.(把所有正确命题的序号填在横线上)
四、解答题
17.已知,,与的夹角为60°.
(1)求:,;(2)求:.
18.已知,,方程的一个根为,复数,满足.
(1)求复数;
(2)若,求复数
19.如图,在三棱柱中,侧面是正方形,M,N分别是,的中点,平面 .
(1)求证:平面平面;
(2)求证:平面;
(3)若三棱柱的体积为10,求三棱锥的体积.
20.在中,,,.
(1)求的长;
(2)求的值.
21.如图,某巡逻艇在A处发现北偏东30°相距海里的B处有一艘走私船,正沿东偏南45°的方向以3海里/小时的速度向我海岸行驶,巡逻艇立即以海里/小时的速度沿着正东方向直线追去,1小时后,巡逻艇到达C处,走私船到达D处,此时走私船发现了巡逻艇,立即改变航向,以原速向正东方向逃窜,巡逻艇立即加速以海里/小时的速度沿着直线追击
(1)当走私船发现了巡逻艇时,两船相距多少海里
(2)问巡逻艇应该沿什么方向去追,才能最快追上走私船
22.如图,在平行四边形中,,,E为的中点,以为折痕将折起,使点D到达点P的位置,且,F,G分别为,的中点.
(1)证明:平面 .
(2)若平面与平面的交线为,求直线与平面所成角的正弦值.
永州市名校2022-2023学年高一下学期6月月考
数学答案
一、单选题(每题5分)
1.B. 2.D 3. D 4.A.5. B
6.C.【详解】设,则,,
,所以,
又,所以,又,
所以.
7. C
【详解】对于A,当时,因为,所以,故不一定成立,选项A错误;
对于B,,所以B错误;
对于C,由,,所以,得出,选项C正确;
对于D,由C选项的分析得,得出,选项D错误.
8. A
【详解】设,
则由可得, ,
两式相加得: ,故,由于,,故 ,
所以由得, ,即,由可得,
二、多选题(每题5分)
9. BCD 10. ABC
当时,即,,,则成立,D正确.
11. ACD
【详解】根据正弦定理,由
,
因为,所以,因此,
因为,所以,因此选项A正确,选项B不正确;
因为是中线,所以由
,或舍去,
因此,所以选项C正确;
△ABC的面积为,所以选项D正确,
12.BD
【详解】设正四棱锥为,其底面中心为;
设正四棱柱为,其下底面中心为,
设是的中点,连接,
是球的球心,设球的半径为,
设正四棱柱的高为,则正四棱锥的高为,为正数,
所以,,
所以,所以,解得,
所以,球的体积,A选项错误.
组合体的体积为,B选项正确.
依题意可知正四棱锥的侧棱与其底面所成角为,
,C选项错误.
根据正四棱锥的性质可知:,
所以是正四棱锥的侧面与其底面的夹角,
,D选项正确.
三、填空题(每题5分)
13. //120°
14.
15.②③④
【详解】还原成正四面体知GH与EF为异面直线,
BD与MN为异面直线,GH与MN成60°角,
因为正四面体对棱垂直,所以,所以DE⊥MN.
16.①②③
【详解】
对于①,取中点,连接,
∵为中点,,,∴四边形为正方形,则
在中,,分别为,的中点,则∥,且
∵为的中点,且∥,∴∥且
∴四边形为平行四边形,∴∥
∴,故①正确;
对于②,∵,,∴
∵面,
∴三棱锥的外接球的球心在线段的中点处,则外接球的半径为
∴三棱锥的外接球的表面积为,故②正确;
对于③,∵,,,
在中,,,,
同理可得,则三棱锥为正四面体,
所以该正四面体的高,底面面积,
体积,故③正确;
对于④,∵面,∴直线在平面上的投影为直线
则为直线与平面所成的角
在中,
∴直线与平面所成的角不是,故④不正确.
故答案为:①②③.
四、解答题(17题10分,18-22每题12分)
17.由得
又
18.(1)依题意,得,即,
由复数相等的定义及a,,得,解得.
故复数.
(2)设(,),由,得,
,
又,得,即,所以,
解得,所以.
19.(1)∵平面,平面,∴,
在正方形中,,∵,∴平面.
∵平面,∴平面平面.
(2)设中点为,连接,∵分别是的中点,
∴,且.又点是的中点,∴.
∵,且,∴,且,
∴四边形是平行四边形,∴.
∵平面,平面, ∴平面.
(3)连接,则,∵为的中点,
∴三棱锥的体积.
20.(1)在中,,由正弦定理得
(2)∵,
因为,所以 ,
∴,,
.
21.(1)由题意知,当走私船发现了巡逻艇时,走私船在D处,巡逻艇在C处,此时,由题意知
在中,由余弦定理得
所以
在中, 由正弦定理得,即
所以(舍去)
所在又
在中,
由余弦定理得
, 故当走私船发现了巡逻艇时,两船相距海里.
(2)当巡逻艇经过小时经方向在处追上走私船,
则
在中,由正弦定理得:
则
所以,
在中,由正弦定理得:
则,故 (舍)
故巡逻艇应该北偏东方向去追,才能最快追上走私船.
22.(1)
连接,交于,并连接,
由、分别是、的中点,而,故为正方形,
所以为的中点,又是的中点,
所以,而面,面,故面.
(2)
由题易知:且均为等腰三角形,且均为等边三角形,
若为中点,连接,则,
而,面,则面,
又面,故面面,面面,
所以在面上的射影在直线上,
过作直线,而,则,故直线为面与面的交线,
所以直线与平面所成角,即为与面所成角,
由题设,,,令,则,,
因为面,面,故,
所以,又,易知,
在△中,,整理得,
所以,故,,
若到面的距离为,且,即,
所以,,,,
综上,,则.
同课章节目录
