面积与代数恒等式[上学期]
图片预览



文档简介
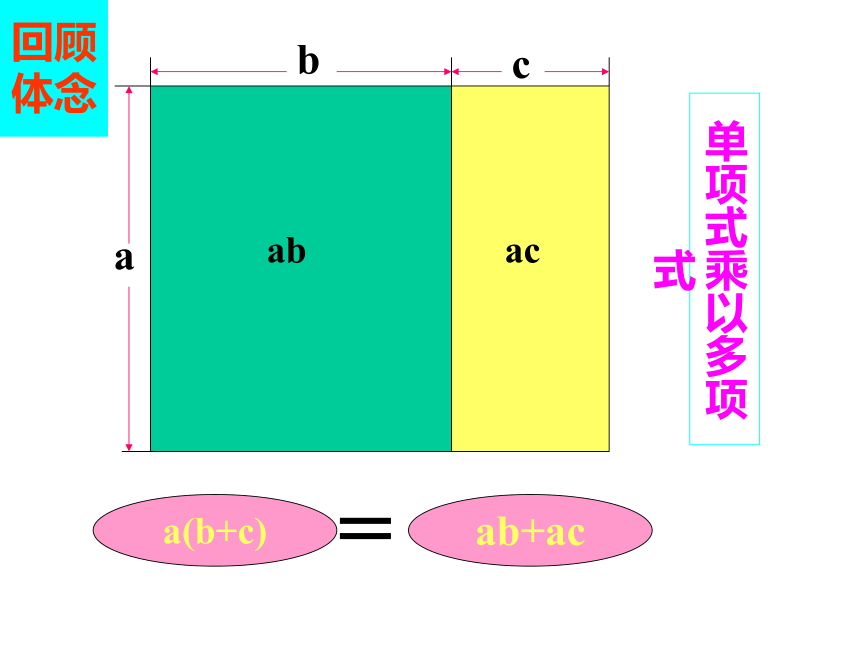
课件21张PPT。实 践 与 探 索 abca(b+c)abacab+ac =单项式乘以多项式回顾
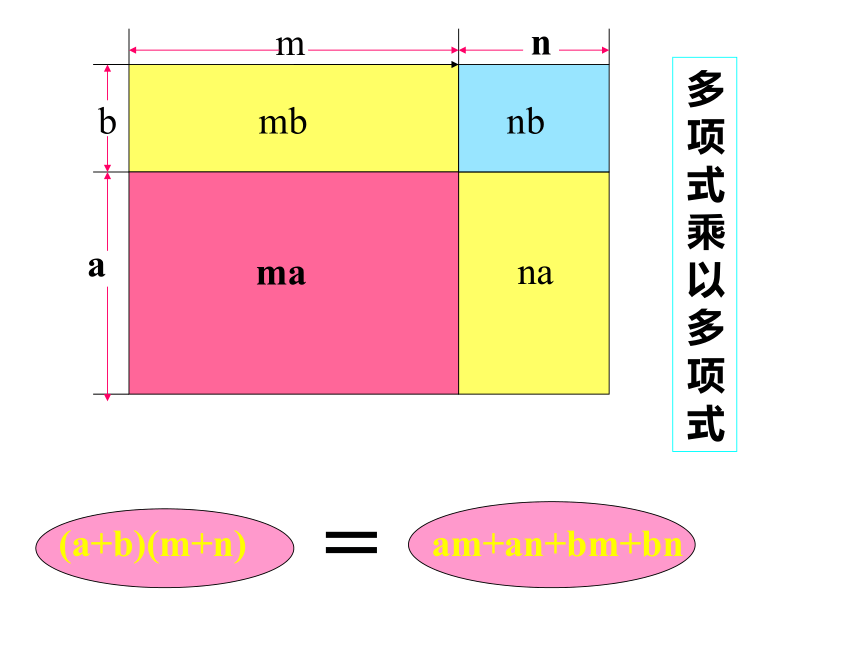
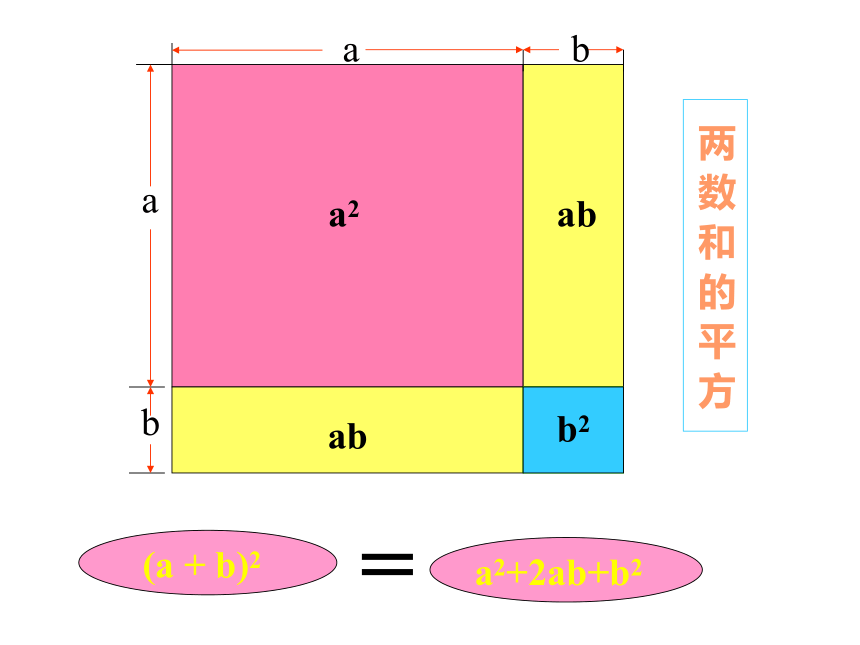
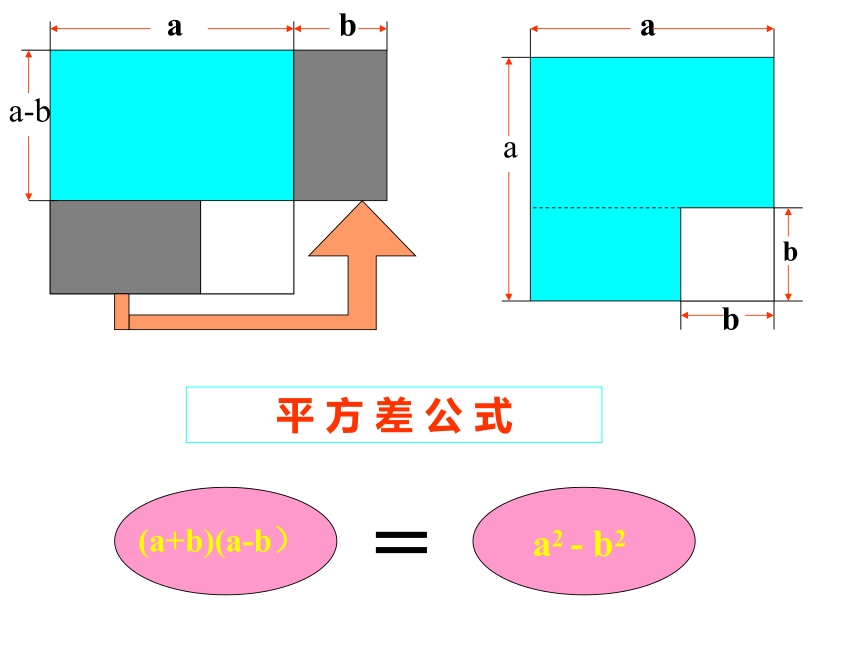
体念ambnnambnbma多 项 式 乘 以 多 项 式(a+b)(m+n)am+an+bm+bn=ababa2ababb2b2=两 数 和 的 平 方(a + b)2a2+2ab+b2aabba2 - b2a-bab(a+b)(a-b)=平 方 差 公 式a(b+c)ab + ac=(m+n)(a+b)mb+nb+ma+na=(a+b)2a2+2ab+b2=a2 - b2(a-b)(a+b)=(a+b)(a+b)= 像上述这种,不论字母取什么值,左边
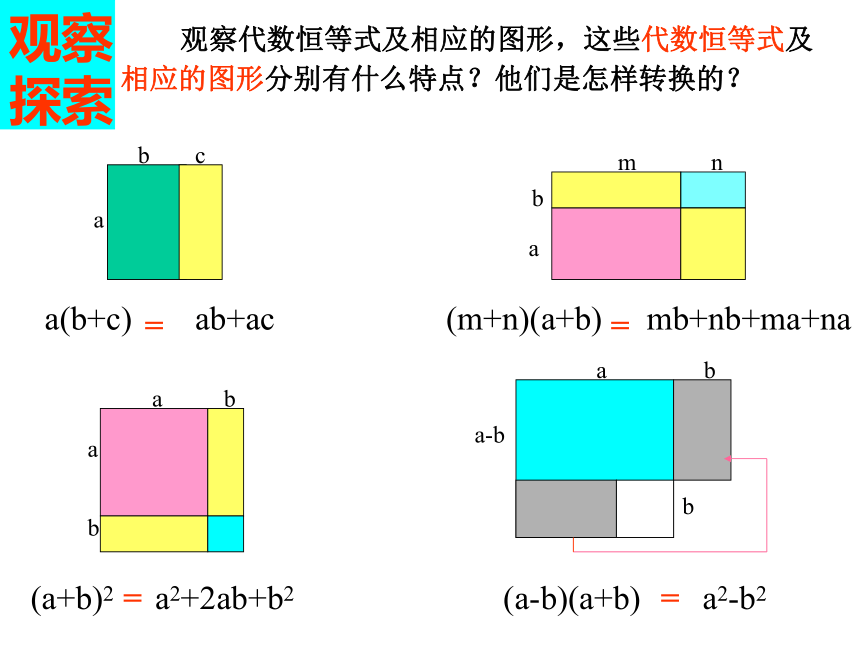
恒等于右边的式子叫做代数恒等式。 这里,又叫二次恒等式 abca(b+c)ab+ac=ambn(m+n)(a+b)mb+nb+ma+na=aabb(a+b)2a2+2ab+b2=a-babba2-b2(a-b)(a+b)= 观察代数恒等式及相应的图形,这些代数恒等式及相应的图形分别有什么特点?他们是怎样转换的?
观察
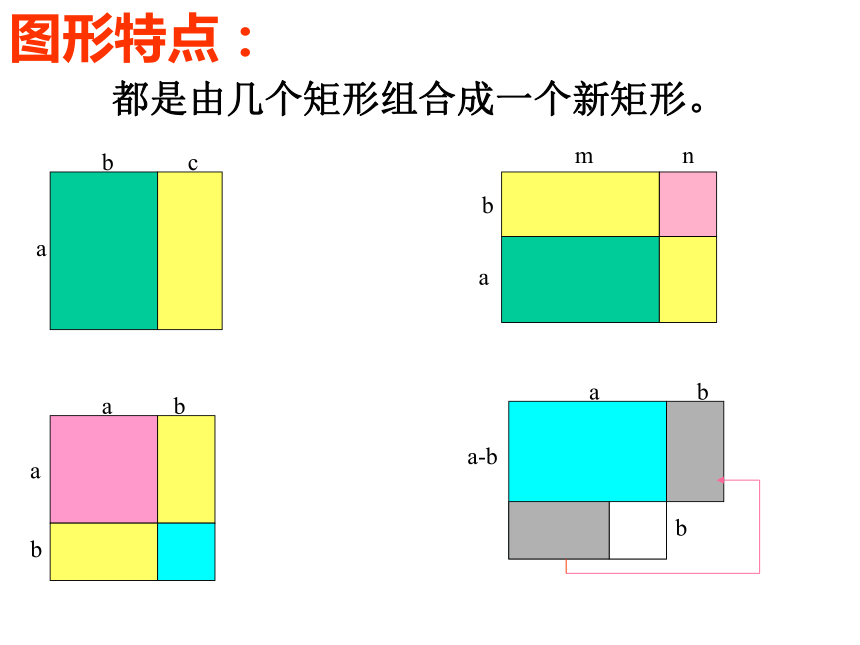
探索a(b+c)ab + ac=(m+n)(a+b)mb+nb+ma+na=(a+b)2a2+2ab+b2=a2 - b2(a-b)(a+b)=代数恒等式特点:一边是两个一次式的积,另一边是二次式。(a+b)(a+b)= abcambnaabba-babb都是由几个矩形组合成一个新矩形。图形特点: abca(b+c)ab+ac=ambn(m+n)(a+b)mb+nb+ma+na=aabb(a+b)2a2+2ab+b2=a-babba2-b2(a-b)(a+b)=二次恒等式图形根据式的几何意义构造图形图形面积的不同表达式 你能利用所准备的若干张小卡片再拼出新的图形吗?根据你所拼的图
实验
与
探索试一试:baba形写出相应的代数 恒等式考考你: 观察下列图形,计算阴影部分的面积,并
用面积的不同表达式写出相应的代数恒等式。abbaa(1)(2)abba(1)解:s阴影=s大正方形-s小正方形=(a+b)2-(a-b)2
s阴影 = 4s小长方形 = 4ab代数恒等式:(a+b)2-(a-b)2=4ababb代数恒等式:(a+b)2-(a-b)2=4abbaaaabbaa代数恒等式:4a2-b2=(2a+b)(2a-b)a(1)(2)想一想 拼一拼 你能根据下列代数式的特点,构造出图形,并利用图形的面积来
(1) (a+b)(a+2b) = a2 + 3ab + 2b2(2) (a+2b)(a-2b) = a2 – ab - 2b2(3) (a-2b)2 = a2 - 4ab + b2说明其正确性吗?aabbba(2)bbS = (a+b)(a-2b)S = a2-ab-2b2bbba(3)abbbbaa--+abS =(a+2b)(a-2b)S =a2-2ab4b2+-2ab拓展
提高 你能判定一个二次多项式是否能因式分解?
如(1)a2+6ab+9b2,(2) 2a2+7ab+3b2 通过这节课的实践探索,你
最大的收获与感想是什么?
课后
思考 1、思考题:是否任意的一个二次代数 请找出反例。2、想一想:为什么根据代数等式构造
恒等式均能用代数恒等式来表示?若不行,出的图形是矩形? 3、若给你四个形状大小完全相同的直
角三角形,你能拼出漂亮的图案吗?再见
体念ambnnambnbma多 项 式 乘 以 多 项 式(a+b)(m+n)am+an+bm+bn=ababa2ababb2b2=两 数 和 的 平 方(a + b)2a2+2ab+b2aabba2 - b2a-bab(a+b)(a-b)=平 方 差 公 式a(b+c)ab + ac=(m+n)(a+b)mb+nb+ma+na=(a+b)2a2+2ab+b2=a2 - b2(a-b)(a+b)=(a+b)(a+b)= 像上述这种,不论字母取什么值,左边
恒等于右边的式子叫做代数恒等式。 这里,又叫二次恒等式 abca(b+c)ab+ac=ambn(m+n)(a+b)mb+nb+ma+na=aabb(a+b)2a2+2ab+b2=a-babba2-b2(a-b)(a+b)= 观察代数恒等式及相应的图形,这些代数恒等式及相应的图形分别有什么特点?他们是怎样转换的?
观察
探索a(b+c)ab + ac=(m+n)(a+b)mb+nb+ma+na=(a+b)2a2+2ab+b2=a2 - b2(a-b)(a+b)=代数恒等式特点:一边是两个一次式的积,另一边是二次式。(a+b)(a+b)= abcambnaabba-babb都是由几个矩形组合成一个新矩形。图形特点: abca(b+c)ab+ac=ambn(m+n)(a+b)mb+nb+ma+na=aabb(a+b)2a2+2ab+b2=a-babba2-b2(a-b)(a+b)=二次恒等式图形根据式的几何意义构造图形图形面积的不同表达式 你能利用所准备的若干张小卡片再拼出新的图形吗?根据你所拼的图
实验
与
探索试一试:baba形写出相应的代数 恒等式考考你: 观察下列图形,计算阴影部分的面积,并
用面积的不同表达式写出相应的代数恒等式。abbaa(1)(2)abba(1)解:s阴影=s大正方形-s小正方形=(a+b)2-(a-b)2
s阴影 = 4s小长方形 = 4ab代数恒等式:(a+b)2-(a-b)2=4ababb代数恒等式:(a+b)2-(a-b)2=4abbaaaabbaa代数恒等式:4a2-b2=(2a+b)(2a-b)a(1)(2)想一想 拼一拼 你能根据下列代数式的特点,构造出图形,并利用图形的面积来
(1) (a+b)(a+2b) = a2 + 3ab + 2b2(2) (a+2b)(a-2b) = a2 – ab - 2b2(3) (a-2b)2 = a2 - 4ab + b2说明其正确性吗?aabbba(2)bbS = (a+b)(a-2b)S = a2-ab-2b2bbba(3)abbbbaa--+abS =(a+2b)(a-2b)S =a2-2ab4b2+-2ab拓展
提高 你能判定一个二次多项式是否能因式分解?
如(1)a2+6ab+9b2,(2) 2a2+7ab+3b2 通过这节课的实践探索,你
最大的收获与感想是什么?
课后
思考 1、思考题:是否任意的一个二次代数 请找出反例。2、想一想:为什么根据代数等式构造
恒等式均能用代数恒等式来表示?若不行,出的图形是矩形? 3、若给你四个形状大小完全相同的直
角三角形,你能拼出漂亮的图案吗?再见
