2023年广东省广州市番禺区中考数学仿真模拟试卷(含答案)
文档属性
| 名称 | 2023年广东省广州市番禺区中考数学仿真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 142.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 15:54:06 | ||
图片预览




文档简介
2023年广东省广州市番禺区中考数学 仿真 模拟 试卷
一、选择题(本大题共10小题,共30.0分)
1. 下列实数中,是无理数的为( )
A. B. C. D.
2. 下列既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B.
C. D.
4. 某县“三独”比赛独唱项目中,名同学的得分分别是:,,,,关于这组数据,下列说法正确的是( )
A. 众数是 B. 中位数是 C. 平均数是 D. 方差是
5. 如图,将沿向右平移得到,若,,则的长是( )
A.
B.
C.
D.
6. 如图,在 中,对角线,相交于点,若,,,则的长为( )
A. B.
C. D.
7. 在“双减政策”的推动下,实外初三学生课后作业时长明显减少年上学期每天作业平均时长为,经过年下学期和年上学期两次调整后,年上学期平均每天作业时长为设这两学期该校平均每天作业时长每期的下降率为,则可列方程为( )
A. B.
C. D.
8. 如图,中,,,,以为圆心的圆弧与相切于点,交于点,交于点,则阴影部分的面积为( )
A.
B.
C.
D.
9. 在某校的科技节活动中,九年级开展了测量教学楼高度的实践活动“阳光小组”决定利用无人机测量教学楼的高度如图,已知无人机与教学楼的水平距离为米,在无人机上测得教学楼底部的俯角为,测得教学楼顶部的仰角为根据以上信息,可以表示教学楼单位:米的高度是( )
A.
B.
C.
D.
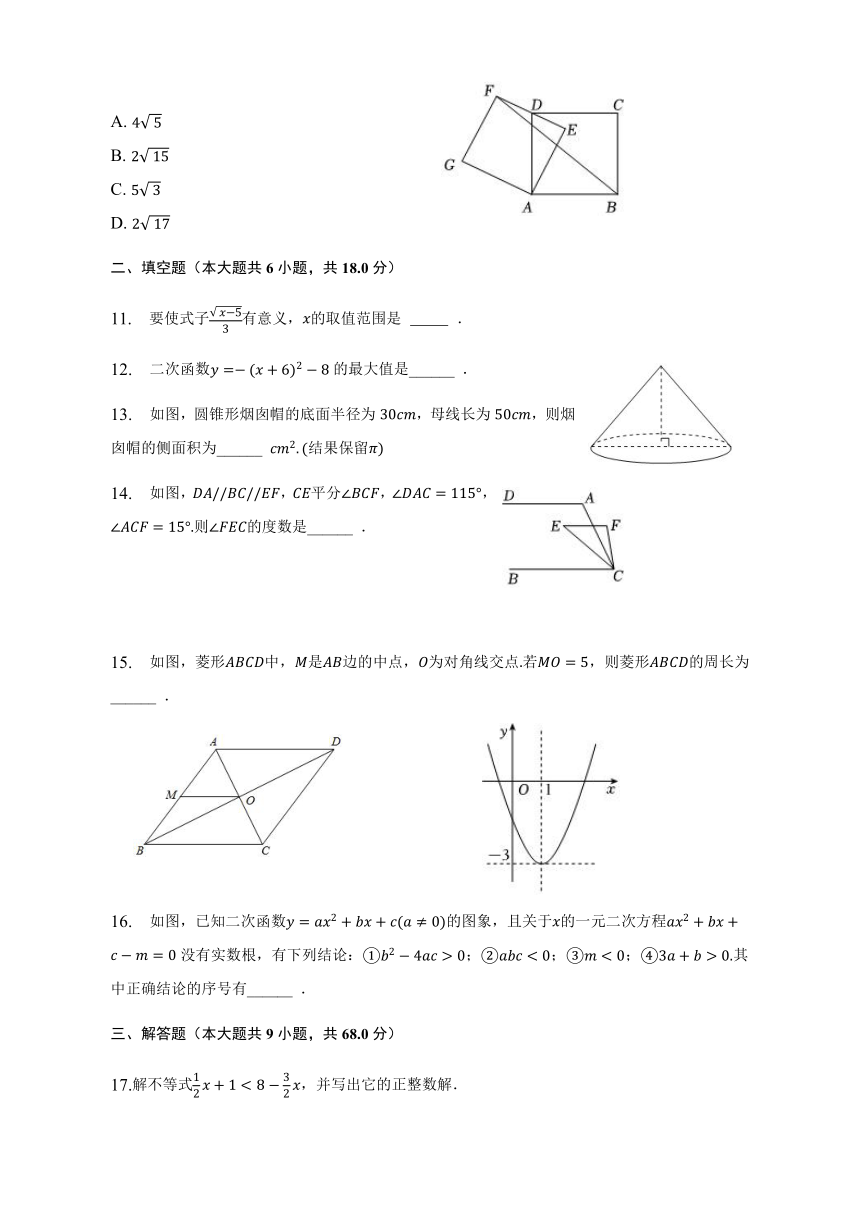
10. 如图,四边形和四边形均为正方形,点为的中点,若,连接,则的长为( )
A.
B.
C.
D.
二、填空题(本大题共6小题,共18.0分)
11. 要使式子有意义,的取值范围是 .
12. 二次函数的最大值是______ .
13. 如图,圆锥形烟囱帽的底面半径为,母线长为,则烟囱帽的侧面积为______ 结果保留
14. 如图,,平分,,则的度数是______ .
15. 如图,菱形中,是边的中点,为对角线交点若,则菱形的周长为______ .
16. 如图,已知二次函数的图象,且关于的一元二次方程没有实数根,有下列结论:;;;其中正确结论的序号有______ .
三、解答题(本大题共9小题,共68.0分)
17.解不等式,并写出它的正整数解.
18.先化简,再求值,请你从的范围内选取一个你喜欢的整数作为的值.
19.中国共产党第二十次全国代表大会胜利闭幕,某市举行“学习二十大,奋进新征程”知识竞答活动,共有道必答选择题,每道选择题都有,,,四个选项,有且只有一个选项是正确的小琳已答对前题,如果答对最后两道题就能顺利通关假设最后这两道题小琳都不会,只能从所有选项中随机选择一个.
小琳答对第题的概率为______ ;
如果小琳在答第题时使用一次“求助”,排除了错误答案B请你用画树状图或列表的方法分析小琳竞答通关的概率有多大?
20.如图,在平行四边形中,点、在对角线上,且求证:.
21. 瑞兔迎春,福满万家吉祥物“兔圆圆”拉开央视总台兔年春晚的帷幕竖直的耳朵、微昂的脑袋、挺起的胸脯等设计巧思,彰显出奋进向上的精气神,某商店用元购进了一批“兔圆圆”玩具,过了一段时间,又用元购进一批“兔圆圆”玩具,所购数量是第一次购进数量的倍,但每个“兔圆圆”玩具的价格比第一次购进的价格贵了元.
商店第一次购进“兔圆圆”玩具多少个?
若该商店两次购进的“兔圆圆”玩具按相同的标价销售,全部售完后利润不低于元,则每个“兔圆圆”玩具的标价至少是多少元?
22.如图,已知直线与双曲线交于,两点.
求直线的解析式;
将直线向下平移个单位后与双曲线交于、两点,与轴交于点,求的面积.
23.如图,以的直角边为直径作,交斜边于点,点是的中点,连接、.
求证:是的切线;
若,,求的长;
求证:.
24.实践与探究
操作一:如图,已知三角形纸片,,,将三角形纸片沿过点的直线折叠,折痕为,点的对应点为点,与交于点,且,则 ______ 度;
操作二:如图,将沿继续折叠,点的对应点为点,与交于点,与交于点,则图中度数为的角共有______ 个
根据以上操作所得结论,解答下列问题:
求证:≌;
若,则线段的长为______ .
25.如图,二次函数经过点、,点是轴正半轴上一个动点,过点作垂直于轴的直线分别交抛物线和直线于点和点设点的横坐标为.
求二次函数的表达式;
若、、三个点中恰有一点是其它两点所连线段的中点三点重合除外时,求的值.
点在线段上时,若以、、为顶点的三角形与相似,求的值.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.
17.解:去分母得:,
移项得:,
合并同类项得:,
系数化为得:.
故正整数解为,,.
18.解:原式
,
在内的整数有,,,,
和,
当时,原式;
19.解:(1)∵每道选择题都有A、B、C,D三个选项,有且只有一个选项是正确的,
∴小明答对第9题的概率是.
(2)假设A表示第9题正确的选项,B、C,D表示第9题错误的选项;A表示第10题正确的选项,B、C,A表示第10题错误的选项;
∵使用一次“求助”可以让主持人在选项中去掉一个错误选项,第10题去掉的错误选项都是B.
树状图如下:
由列表可知,共有12种等可能的结果,小明顺利通过的只有1种情况,所以小明能够顺利通关的概率为.
20.证明:四边形是平行四边形,
,,
,
在和中,
,
≌,
.
21.解:设商店第一次购进“兔圆圆”玩具个,
根据题意,得,
解得,
经检验,是原方程的根,且符合题意,
答:商店第一次购进“兔圆圆”玩具个;
设每个“兔圆圆”玩具的标价为元,
个,
根据题意,得,
解得,
每个“兔圆圆”玩具的标价至少为元.
22.解:直线与双曲线交于,两点,
,
,,
,,
,
解得,
直线的解析式为;
设直线与轴交于点,连接,
由题意可知,,
,
将直线向下平移个单位后得到,
由,解得或,
,
,
的面积为.
23.证明:连接,,
在中,,
是的直径,
,
,
点是的中点,
,
、是的半径,
,
又,
≌,
,
半径,
是的切线;
解:连接,如图,
由知:,,
,
,
,
,
,
,
,
,
,
设,则,
,
,
解得:负值舍去,
;
证明:连接,
由得:,,
点是的中点,点是的中点,
,,
,
∽,
,即,
.
24.操作一:
操作二:
证明:,,
,
,
,
为等腰直角三角形,
,
在和中,
,
≌.
25.解:把、代入得:
,
解得:,
;
、,
设直线的解析式为,把、坐标代入得:
,
解得:,
直线的解析式为;
,
则,,
,,
当为线段的中点时,则有,
即:,
解得三点重合,舍去或,
;
,,
,
由可知:、,,,
,
以、、为顶点的三角形与相似,分两种情况讨论:
当为直角时,则,
,即:,
,即:
解得:舍去,;
当为直角时,则,
,即:,
,即:,
解得,舍去,
综上所述,的值是或.
一、选择题(本大题共10小题,共30.0分)
1. 下列实数中,是无理数的为( )
A. B. C. D.
2. 下列既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B.
C. D.
4. 某县“三独”比赛独唱项目中,名同学的得分分别是:,,,,关于这组数据,下列说法正确的是( )
A. 众数是 B. 中位数是 C. 平均数是 D. 方差是
5. 如图,将沿向右平移得到,若,,则的长是( )
A.
B.
C.
D.
6. 如图,在 中,对角线,相交于点,若,,,则的长为( )
A. B.
C. D.
7. 在“双减政策”的推动下,实外初三学生课后作业时长明显减少年上学期每天作业平均时长为,经过年下学期和年上学期两次调整后,年上学期平均每天作业时长为设这两学期该校平均每天作业时长每期的下降率为,则可列方程为( )
A. B.
C. D.
8. 如图,中,,,,以为圆心的圆弧与相切于点,交于点,交于点,则阴影部分的面积为( )
A.
B.
C.
D.
9. 在某校的科技节活动中,九年级开展了测量教学楼高度的实践活动“阳光小组”决定利用无人机测量教学楼的高度如图,已知无人机与教学楼的水平距离为米,在无人机上测得教学楼底部的俯角为,测得教学楼顶部的仰角为根据以上信息,可以表示教学楼单位:米的高度是( )
A.
B.
C.
D.
10. 如图,四边形和四边形均为正方形,点为的中点,若,连接,则的长为( )
A.
B.
C.
D.
二、填空题(本大题共6小题,共18.0分)
11. 要使式子有意义,的取值范围是 .
12. 二次函数的最大值是______ .
13. 如图,圆锥形烟囱帽的底面半径为,母线长为,则烟囱帽的侧面积为______ 结果保留
14. 如图,,平分,,则的度数是______ .
15. 如图,菱形中,是边的中点,为对角线交点若,则菱形的周长为______ .
16. 如图,已知二次函数的图象,且关于的一元二次方程没有实数根,有下列结论:;;;其中正确结论的序号有______ .
三、解答题(本大题共9小题,共68.0分)
17.解不等式,并写出它的正整数解.
18.先化简,再求值,请你从的范围内选取一个你喜欢的整数作为的值.
19.中国共产党第二十次全国代表大会胜利闭幕,某市举行“学习二十大,奋进新征程”知识竞答活动,共有道必答选择题,每道选择题都有,,,四个选项,有且只有一个选项是正确的小琳已答对前题,如果答对最后两道题就能顺利通关假设最后这两道题小琳都不会,只能从所有选项中随机选择一个.
小琳答对第题的概率为______ ;
如果小琳在答第题时使用一次“求助”,排除了错误答案B请你用画树状图或列表的方法分析小琳竞答通关的概率有多大?
20.如图,在平行四边形中,点、在对角线上,且求证:.
21. 瑞兔迎春,福满万家吉祥物“兔圆圆”拉开央视总台兔年春晚的帷幕竖直的耳朵、微昂的脑袋、挺起的胸脯等设计巧思,彰显出奋进向上的精气神,某商店用元购进了一批“兔圆圆”玩具,过了一段时间,又用元购进一批“兔圆圆”玩具,所购数量是第一次购进数量的倍,但每个“兔圆圆”玩具的价格比第一次购进的价格贵了元.
商店第一次购进“兔圆圆”玩具多少个?
若该商店两次购进的“兔圆圆”玩具按相同的标价销售,全部售完后利润不低于元,则每个“兔圆圆”玩具的标价至少是多少元?
22.如图,已知直线与双曲线交于,两点.
求直线的解析式;
将直线向下平移个单位后与双曲线交于、两点,与轴交于点,求的面积.
23.如图,以的直角边为直径作,交斜边于点,点是的中点,连接、.
求证:是的切线;
若,,求的长;
求证:.
24.实践与探究
操作一:如图,已知三角形纸片,,,将三角形纸片沿过点的直线折叠,折痕为,点的对应点为点,与交于点,且,则 ______ 度;
操作二:如图,将沿继续折叠,点的对应点为点,与交于点,与交于点,则图中度数为的角共有______ 个
根据以上操作所得结论,解答下列问题:
求证:≌;
若,则线段的长为______ .
25.如图,二次函数经过点、,点是轴正半轴上一个动点,过点作垂直于轴的直线分别交抛物线和直线于点和点设点的横坐标为.
求二次函数的表达式;
若、、三个点中恰有一点是其它两点所连线段的中点三点重合除外时,求的值.
点在线段上时,若以、、为顶点的三角形与相似,求的值.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.
17.解:去分母得:,
移项得:,
合并同类项得:,
系数化为得:.
故正整数解为,,.
18.解:原式
,
在内的整数有,,,,
和,
当时,原式;
19.解:(1)∵每道选择题都有A、B、C,D三个选项,有且只有一个选项是正确的,
∴小明答对第9题的概率是.
(2)假设A表示第9题正确的选项,B、C,D表示第9题错误的选项;A表示第10题正确的选项,B、C,A表示第10题错误的选项;
∵使用一次“求助”可以让主持人在选项中去掉一个错误选项,第10题去掉的错误选项都是B.
树状图如下:
由列表可知,共有12种等可能的结果,小明顺利通过的只有1种情况,所以小明能够顺利通关的概率为.
20.证明:四边形是平行四边形,
,,
,
在和中,
,
≌,
.
21.解:设商店第一次购进“兔圆圆”玩具个,
根据题意,得,
解得,
经检验,是原方程的根,且符合题意,
答:商店第一次购进“兔圆圆”玩具个;
设每个“兔圆圆”玩具的标价为元,
个,
根据题意,得,
解得,
每个“兔圆圆”玩具的标价至少为元.
22.解:直线与双曲线交于,两点,
,
,,
,,
,
解得,
直线的解析式为;
设直线与轴交于点,连接,
由题意可知,,
,
将直线向下平移个单位后得到,
由,解得或,
,
,
的面积为.
23.证明:连接,,
在中,,
是的直径,
,
,
点是的中点,
,
、是的半径,
,
又,
≌,
,
半径,
是的切线;
解:连接,如图,
由知:,,
,
,
,
,
,
,
,
,
,
设,则,
,
,
解得:负值舍去,
;
证明:连接,
由得:,,
点是的中点,点是的中点,
,,
,
∽,
,即,
.
24.操作一:
操作二:
证明:,,
,
,
,
为等腰直角三角形,
,
在和中,
,
≌.
25.解:把、代入得:
,
解得:,
;
、,
设直线的解析式为,把、坐标代入得:
,
解得:,
直线的解析式为;
,
则,,
,,
当为线段的中点时,则有,
即:,
解得三点重合,舍去或,
;
,,
,
由可知:、,,,
,
以、、为顶点的三角形与相似,分两种情况讨论:
当为直角时,则,
,即:,
,即:
解得:舍去,;
当为直角时,则,
,即:,
,即:,
解得,舍去,
综上所述,的值是或.
同课章节目录
