27.2.1 相似三角形的判定 说课课件(共31张PPT)数学人教版九年级下册
文档属性
| 名称 | 27.2.1 相似三角形的判定 说课课件(共31张PPT)数学人教版九年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 16:44:43 | ||
图片预览






文档简介
(共31张PPT)
相似三角形的判定
选自人教九年级下
《27.2.1相似三角形的判定》第一课时
教学背景分析
教学特点的说明
教学目标的确定
教学的重点和难点
教学过程的设计
一、教学背景分析
教学内容的
地位与作用
平行线分线段成比例定理是研究相似三角形的最重要和最基本的理论,是后面四个判定的基础,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比来证明。
学生情况分析
一、教学背景分析
具有直观的感知经验
预备定理的证明有一定困难
教学方式
启发讲授
与探究相结合
PPT课件 圆规 直尺
教学准备
二、教学目标的确定
知识与技能:理解平行线分线段成比例,并会利用此定理证明相似三角形的判定的预备定理。
过程与方法:经历直观感知、测量验证、操作确认的过程,培养学生合情推理,有条理使用数学语言,关注基本几何模型。
情感态度价值观:体会将特殊转化为一般问题的方法。
三、教学的重点和难点
重点
理解平行线分线段成比例定理及其推论,掌握三角形相似的第一个判定定理。
难点
用平行判定三角形相似定理的探究、证明过程。
巩固所学
应用定理
操作确认
引入课题
四、教学过程的设计
归纳小结
例题分析
直观感知
创设情境
活动1
活动2
活动3
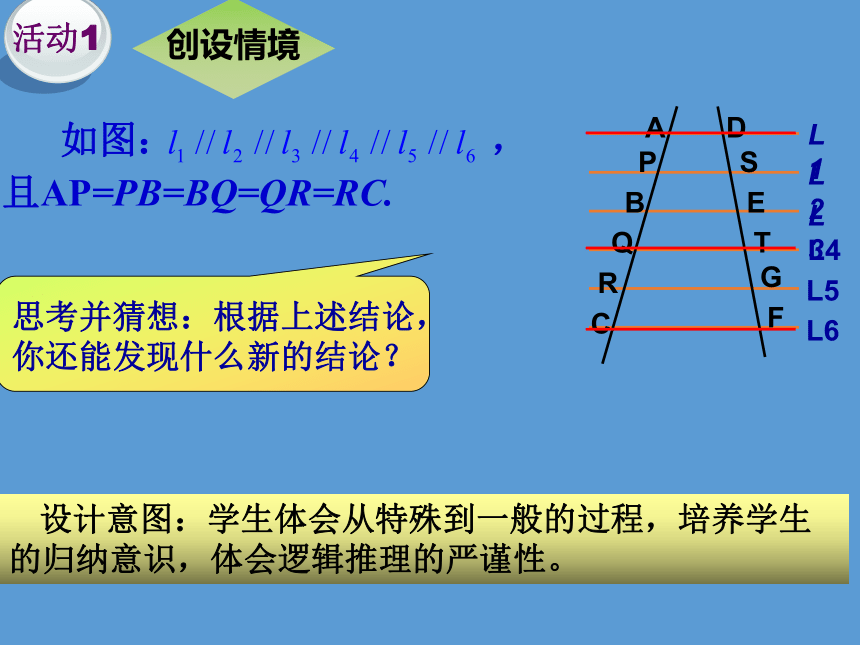
创设情境
设计意图:学生体会从特殊到一般的过程,培养学生的归纳意识,体会逻辑推理的严谨性。
A
P
B
Q
R
C
D
S
E
T
G
F
L1
L2
L3
L4
L5
L6
思考并猜想:根据上述结论,你还能发现什么新的结论?
如图: ,
且AP=PB=BQ=QR=RC.
活动1
A
B
C
D
E
F
l1
l2
l3
P1
P2
P3
Q1
Q2
Q3
a1
a1
a3
l
l
活动1
a
A
B
C
D
E
F
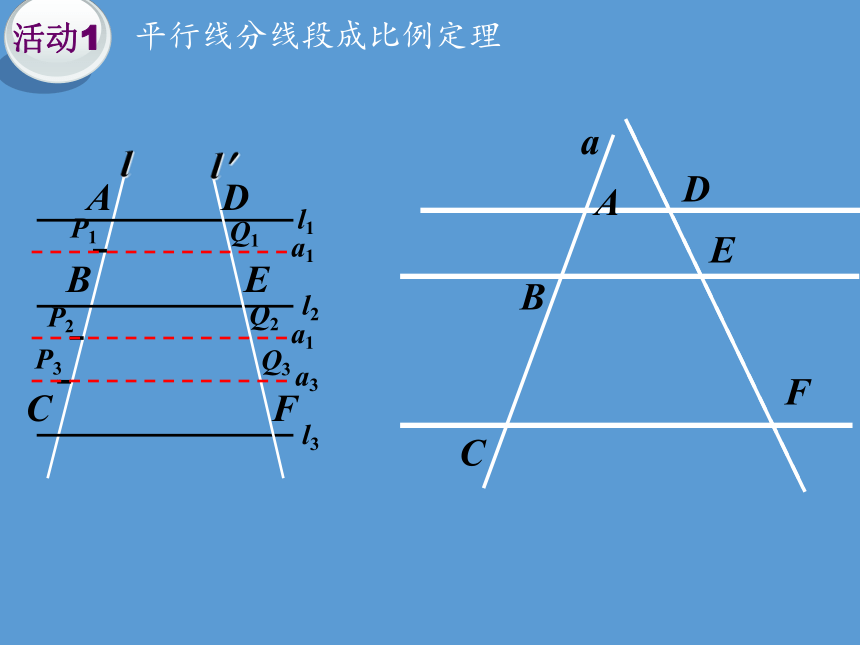
平行线分线段成比例定理
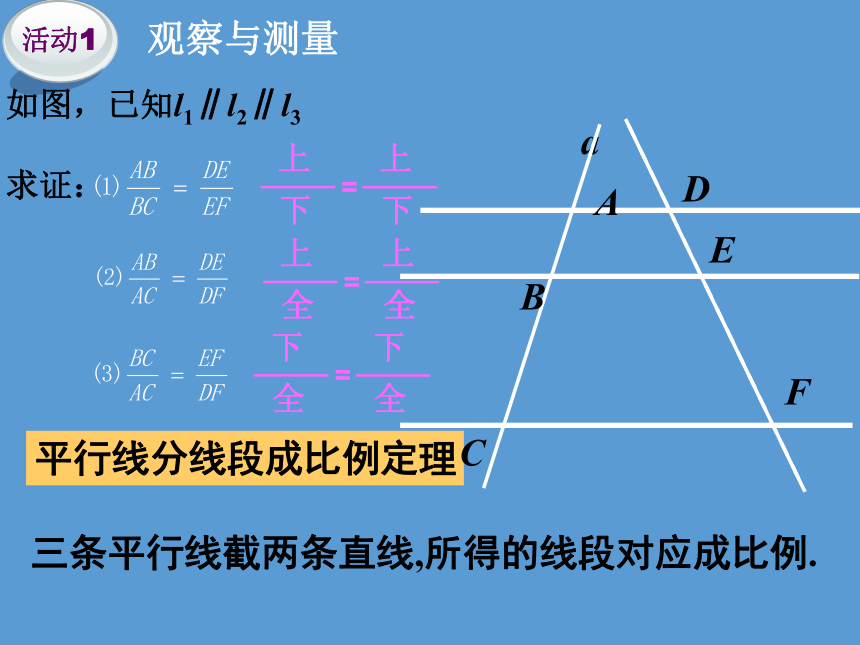
如图,已知l1∥l2∥l3
求证:
观察与测量
平行线分线段成比例定理
三条平行线截两条直线,所得的线段对应成比例.
上
下
上
下
=
上
全
上
全
=
下
全
下
全
=
活动1
a
A
B
C
D
E
F
a
b
l1
l2
l3
A
B
C
D
E
F
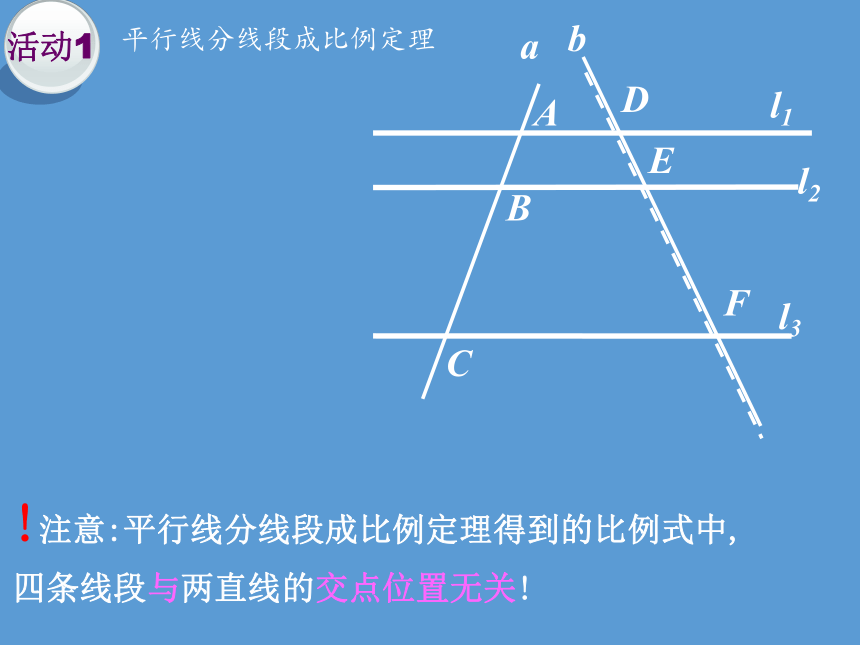
!注意:平行线分线段成比例定理得到的比例式中,
四条线段与两直线的交点位置无关!
活动1
平行线分线段成比例定理
a
b
l1
l2
l3
A
B
C
D
E
F
活动1
平行线分线段成比例定理
质疑反思
直观感知
活动1
活动2
活动3
a
b
基本图形:“A”字形
l1
l2
l3
A
B
C
(D)
E
F
活动2
推论生成过程
a
b
基本图形:“8”字形
l1
l2
l3
A
B
C
D
(E)
F
活动2
推论生成过程
推论:平行于三角形一边的直线截其他两(或两边的延长线),所得的对应线段的比相等。
教学设计
观察
A
D
B
F
E
C
L1
L2
L3
图1
(
)
F
A
D
B
C
L1
L2
L3
图3
怎样变化?
一般到特殊
平行移动直线FC与直线AB相交,交点D在L2上
(E)
教学设计(2)
思考:把图2、图3中的部分线擦去,得到图4、图5,上述比例式还成立吗?
A
D
B
E
L1
L2
L3
C
部分线擦去,取一部分
A
D
B
E
C
(
)
字母 型
A
比例式
,
因为
图2
图4
一般到特殊
成立
图形中有关的对应线段均没改变
教学设计(2)续
续思考
F
A
D
B
C
(E)
图3
部分线擦去,取一部分
F
A
D
(E)
B
C
图5
(字母 型)
比例式
,
因为
一般到特殊
成立
图形中有关的对应线段均没改变
X
如图,在△ABC 中,DE//BC,
DE分别交AB,AC 于点D,E,
△ADE与△ABC有什么关系
思
考
?
活动3
三角形相似预备定理
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
活动3
先证明两个三角形的对应角相等.
方案一
三角形相似预备定理
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
∴△ADE∽△ABC
活动3
方案二
三角形相似预备定理
质疑反思
知识形成
图形语言
文字语言
符号语言
字母 型 字母 型
A
D
E
B
C
F
A
D
B
C
图4
图5
若DE∥BC则: 若AF∥BC则:
A
X
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
模型语言
四、教学过程的设计
归纳小结
例题分析
直观感知
创设情境
巩固所学
应用定理
操作确认
引入课题
例 题 1
CE
BE
BC
CE
AD
AC
AE
EB
DF
FC
DF
DE
DF
FE
例 题 2
6
9
4
EC=( )
12
15
9
10
AE=( )
GC=( )
3
4
6
AD=( )
6
8
6
14
例3
找到对应的三角形
引导学生
分析思路
自行完成
证明
根据题目
找到线段
相互展示
评价反思
E
E
A
B
C
D
E
F
G
A
B
C
D
F
G
A
B
D
C
F
G
A
D
B
C
F
G
E
四、教学过程的设计
归纳小结
例题分析
直观感知
创设情境
巩固所学
应用定理
操作确认
引入课题
归纳小结
1、平行线分线段成比例定理是研究相似形最重要、最基本的理论基础,而字母A型、字母X型又是解决相似三角形一章有关计算和证明的模具,可构造或寻找字母A型、字母X型解决问题,把它称为三角形相似问题“奠基法”
2、学会用“动态”的观点去解决研究问题。
3、欣赏模型“字母A型、字母X型”的理性美、结构美,诱发学习数学的激情,感受数学的美学文化,培养学生“自主实践、自主探索、大胆猜想、归纳创新”的数学理念。
五、教学特点的说明
注重学生直观感知、操作确认
体现将图形问题转化为对应线段问题
合情推理、有条理的表达
谢谢
各位专家的指导!
相似三角形的判定
选自人教九年级下
《27.2.1相似三角形的判定》第一课时
教学背景分析
教学特点的说明
教学目标的确定
教学的重点和难点
教学过程的设计
一、教学背景分析
教学内容的
地位与作用
平行线分线段成比例定理是研究相似三角形的最重要和最基本的理论,是后面四个判定的基础,它一方面可以直接判定线段成比例,另一方面,当不能直接证明要证的比例成立时,常用这个定理把两条线段的比“转移”成另两条线段的比来证明。
学生情况分析
一、教学背景分析
具有直观的感知经验
预备定理的证明有一定困难
教学方式
启发讲授
与探究相结合
PPT课件 圆规 直尺
教学准备
二、教学目标的确定
知识与技能:理解平行线分线段成比例,并会利用此定理证明相似三角形的判定的预备定理。
过程与方法:经历直观感知、测量验证、操作确认的过程,培养学生合情推理,有条理使用数学语言,关注基本几何模型。
情感态度价值观:体会将特殊转化为一般问题的方法。
三、教学的重点和难点
重点
理解平行线分线段成比例定理及其推论,掌握三角形相似的第一个判定定理。
难点
用平行判定三角形相似定理的探究、证明过程。
巩固所学
应用定理
操作确认
引入课题
四、教学过程的设计
归纳小结
例题分析
直观感知
创设情境
活动1
活动2
活动3
创设情境
设计意图:学生体会从特殊到一般的过程,培养学生的归纳意识,体会逻辑推理的严谨性。
A
P
B
Q
R
C
D
S
E
T
G
F
L1
L2
L3
L4
L5
L6
思考并猜想:根据上述结论,你还能发现什么新的结论?
如图: ,
且AP=PB=BQ=QR=RC.
活动1
A
B
C
D
E
F
l1
l2
l3
P1
P2
P3
Q1
Q2
Q3
a1
a1
a3
l
l
活动1
a
A
B
C
D
E
F
平行线分线段成比例定理
如图,已知l1∥l2∥l3
求证:
观察与测量
平行线分线段成比例定理
三条平行线截两条直线,所得的线段对应成比例.
上
下
上
下
=
上
全
上
全
=
下
全
下
全
=
活动1
a
A
B
C
D
E
F
a
b
l1
l2
l3
A
B
C
D
E
F
!注意:平行线分线段成比例定理得到的比例式中,
四条线段与两直线的交点位置无关!
活动1
平行线分线段成比例定理
a
b
l1
l2
l3
A
B
C
D
E
F
活动1
平行线分线段成比例定理
质疑反思
直观感知
活动1
活动2
活动3
a
b
基本图形:“A”字形
l1
l2
l3
A
B
C
(D)
E
F
活动2
推论生成过程
a
b
基本图形:“8”字形
l1
l2
l3
A
B
C
D
(E)
F
活动2
推论生成过程
推论:平行于三角形一边的直线截其他两(或两边的延长线),所得的对应线段的比相等。
教学设计
观察
A
D
B
F
E
C
L1
L2
L3
图1
(
)
F
A
D
B
C
L1
L2
L3
图3
怎样变化?
一般到特殊
平行移动直线FC与直线AB相交,交点D在L2上
(E)
教学设计(2)
思考:把图2、图3中的部分线擦去,得到图4、图5,上述比例式还成立吗?
A
D
B
E
L1
L2
L3
C
部分线擦去,取一部分
A
D
B
E
C
(
)
字母 型
A
比例式
,
因为
图2
图4
一般到特殊
成立
图形中有关的对应线段均没改变
教学设计(2)续
续思考
F
A
D
B
C
(E)
图3
部分线擦去,取一部分
F
A
D
(E)
B
C
图5
(字母 型)
比例式
,
因为
一般到特殊
成立
图形中有关的对应线段均没改变
X
如图,在△ABC 中,DE//BC,
DE分别交AB,AC 于点D,E,
△ADE与△ABC有什么关系
思
考
?
活动3
三角形相似预备定理
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
活动3
先证明两个三角形的对应角相等.
方案一
三角形相似预备定理
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
∴△ADE∽△ABC
活动3
方案二
三角形相似预备定理
质疑反思
知识形成
图形语言
文字语言
符号语言
字母 型 字母 型
A
D
E
B
C
F
A
D
B
C
图4
图5
若DE∥BC则: 若AF∥BC则:
A
X
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
模型语言
四、教学过程的设计
归纳小结
例题分析
直观感知
创设情境
巩固所学
应用定理
操作确认
引入课题
例 题 1
CE
BE
BC
CE
AD
AC
AE
EB
DF
FC
DF
DE
DF
FE
例 题 2
6
9
4
EC=( )
12
15
9
10
AE=( )
GC=( )
3
4
6
AD=( )
6
8
6
14
例3
找到对应的三角形
引导学生
分析思路
自行完成
证明
根据题目
找到线段
相互展示
评价反思
E
E
A
B
C
D
E
F
G
A
B
C
D
F
G
A
B
D
C
F
G
A
D
B
C
F
G
E
四、教学过程的设计
归纳小结
例题分析
直观感知
创设情境
巩固所学
应用定理
操作确认
引入课题
归纳小结
1、平行线分线段成比例定理是研究相似形最重要、最基本的理论基础,而字母A型、字母X型又是解决相似三角形一章有关计算和证明的模具,可构造或寻找字母A型、字母X型解决问题,把它称为三角形相似问题“奠基法”
2、学会用“动态”的观点去解决研究问题。
3、欣赏模型“字母A型、字母X型”的理性美、结构美,诱发学习数学的激情,感受数学的美学文化,培养学生“自主实践、自主探索、大胆猜想、归纳创新”的数学理念。
五、教学特点的说明
注重学生直观感知、操作确认
体现将图形问题转化为对应线段问题
合情推理、有条理的表达
谢谢
各位专家的指导!
