相似三角形的性质 说课课件(共43张PPT)
文档属性
| 名称 | 相似三角形的性质 说课课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 998.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 16:09:41 | ||
图片预览






文档简介
(共43张PPT)
相似三角形
的性质
学号:xxxxx
姓名:xxxxx
班级:教学三班
相似三角形的性质
教法分析
学法指导
教学评价
教学流程
教材分析
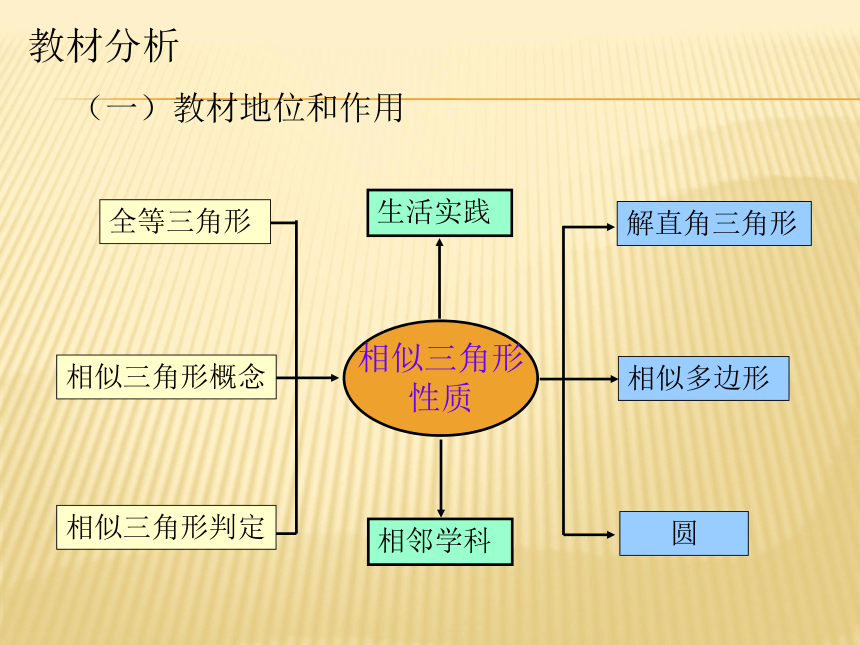
教材分析
(一)教材地位和作用
生活实践
相邻学科
解直角三角形
相似多边形
圆
相似三角形判定
相似三角形概念
全等三角形
相似三角形
性质
(二)教学目标
教学目标
认知目标
技能目标
能力目标
情感目标
理解相似三角形性质
学会相似三角形性质的基本应用
提高观察、分析、综合判断能力
培养学生自主探索的能力
通过渗透类比的数学思想方法,让
学生体验特殊与一般的辩证关系
(三)教学重点难点
重点:相似三角形的性质
难点:相似三角形面积之比结论的得出
及相似三角形性质的应用
教法分析
比
较
、
探
索
(1)通过对相似三角形的回顾,引导学生对
相似三角形性质进行探索、类比,提出猜想
(2)通过“猜想——论证”的方式让学生感受知
识的形成及应用过程
(3)通过例题的变式、延伸,来培养学生的自主
探索的能力
学法指导
遵循因材施教的原则,根据学生已有的知识
水平和认知结构作出如下指导:
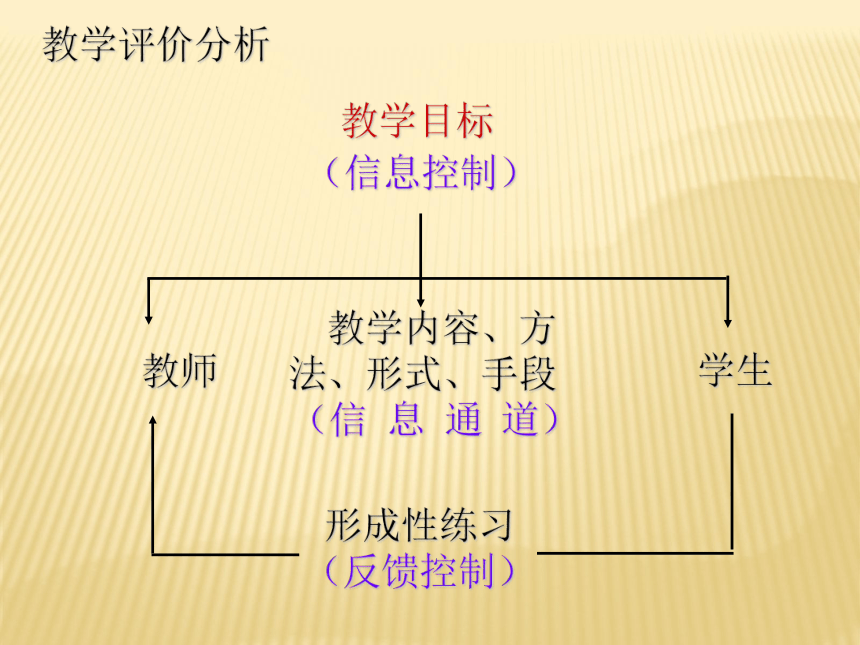
教学评价分析
教学目标
教师
教学内容、方法、形式、手段
(信 息 通 道)
学生
形成性练习
(反馈控制)
(信息控制)
教学流程
情景引入
课前复习
自主思考
探索新知
讲解例题
培养能力
分层练习
巩固应用
课堂小结
布置作业
探求
获取
建构
知识主线
相似三角形的性质
能力主线
训练学生思维
课前复习:
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
A
B
C
A/
B/
C/
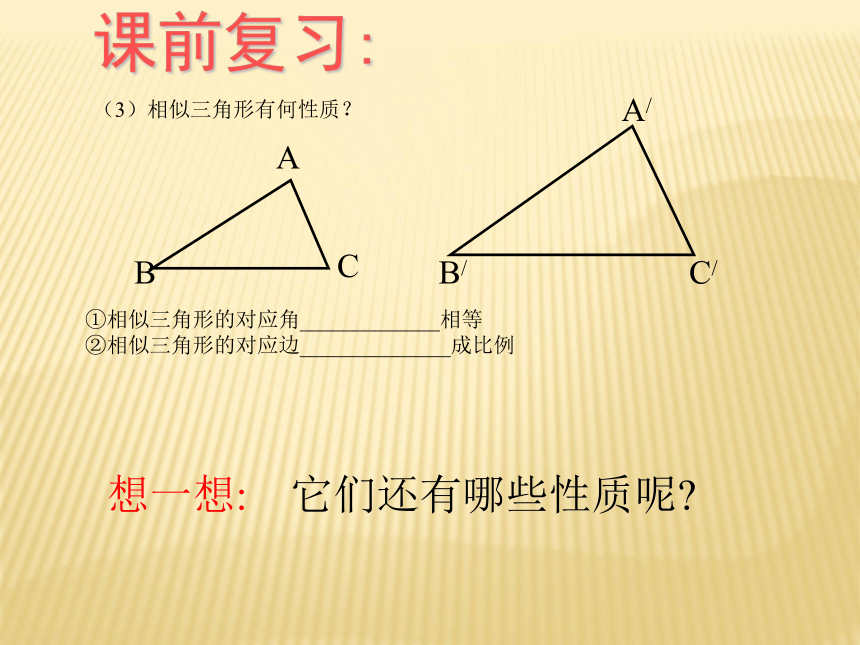
①相似三角形的对应角_____________相等
②相似三角形的对应边______________成比例
想一想: 它们还有哪些性质呢
课前复习:
(3)相似三角形有何性质?
一个三角形有三条重要线段:
________________
如果两个三角形相似,
那么这些对应线段有什么关系呢?
情境引入
高、中线、角平分线
A
C
B
A′
B′
C′
∽
(1)
观察
A
C
B
A′
B′
C′
∽
(2)
A
C
B
A′
B′
C′
∽
(3)
∽
可得:
小结
观察这些数据,你会有怎样的猜想呢?
探索新知
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′( )
相似三角形的对应角相等
∽
( )
相似三角形的性质
探索新知
∽
所以
(相似三角形的对应边成比例)
∽
∽
相似三角形的性质
结论:相似三角形对应高的比等于相似比.
类似结论
D'
C'
B'
A'
D
C
B
A
∽
自主思考---
结论:相似三角形对应中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
填一填
1.相似三角形对应边的比为 2:3 那么相似比为_______,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
问题: 两个相似三角形的周长比
相似三角形的性质
会等于相似比吗?
图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
用心观察
(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______
1∶ 2
结论:相似三角形的周长比等于______.
相似比
(都相似)
2∶ 3
1∶ 2
2∶ 3
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
问题:两个相似三角形的面积
之间有什么关系呢?
相似三角形的性质
用心观察
1
2
3
1∶ 2
当相似比=k时,面积比=k2.
(1)
(2)
(3)
(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______
1∶ 4
2∶ 3
4∶ 9
相似三角形面积的比等于相似比的平方.
例5:已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高,求证:
证明:
∵△ABC∽△
∴
∴
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
面积的比等于相似比的平方
相似三角形的性质
1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.
2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.
3∶5
2:5
巩固应用
2:5
2:5
4:25
3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
(3)两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是______ ____。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。
25
10
100cm、40cm
50cm2、8cm2
4.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗
如果相似,求出△A1B1C1和△A2B2C2的面积比.
2 : 1
解:相似.
因为相似比是
所以面积比是
4 : 1
5.如图,在 ABCD中,若E是AB的中点,
则(1) AEF与 CDF的相似比为______.
(2)若 AEF的面积为5 cm2,
则 CDF的面积为______.
B
F
E
D
C
A
1 : 2
20 cm2
∵ AEF与 CDF
1:已知△ABC∽△DEF,BG、EH分别是△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。
解:∵ △ABC∽△DEF
∴ BC∶EF=BG∶EH
6∶4=4.8∶EH
EH=3.2(cm)
答:EH的长为3.2cm。
A
G
B
C
D
E
F
H
分层练习
2:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。
C'
B'
A'
C
B
A
解:因为△ABC~△A'B'C' △ABC
所以
=
=
AB
BC
A'B'
B'C'
60
72
又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米
故 AC=60–15–20=25(厘米)A'C'=72–18–24=30(厘米)
1、相似三角形对应边成____, 对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
相似多边形也有同样的结论
比例
相等
相似比
相似比
1、已知两个等边三角形的边长之比为 2 :3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?
拓展训练
拓展训练
2、平行四边形ABCD与平行四边形 相似,
已知AB=5,对应边 =6,平行四边形
ABCD的面积为10,求平行四边形
的面积.
已知△ABC∽△ ,且相似比为k。
求证:△ABC、 周长的比等于k
证明:
△ABC∽△
即△ABC、△ 的周长比等于相似比
∵
∴
∴
3、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
提高拓展
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
变式训练
4、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
(2)若AD=10,求ED的长
[板书设计]
相似三角形的性质
定理…… 例1…… 小结 (1)……
…… …… (2)……
定理…… 例2…… (3)……
…… …… (4)……
学生板演
谢谢指导
相似三角形
的性质
学号:xxxxx
姓名:xxxxx
班级:教学三班
相似三角形的性质
教法分析
学法指导
教学评价
教学流程
教材分析
教材分析
(一)教材地位和作用
生活实践
相邻学科
解直角三角形
相似多边形
圆
相似三角形判定
相似三角形概念
全等三角形
相似三角形
性质
(二)教学目标
教学目标
认知目标
技能目标
能力目标
情感目标
理解相似三角形性质
学会相似三角形性质的基本应用
提高观察、分析、综合判断能力
培养学生自主探索的能力
通过渗透类比的数学思想方法,让
学生体验特殊与一般的辩证关系
(三)教学重点难点
重点:相似三角形的性质
难点:相似三角形面积之比结论的得出
及相似三角形性质的应用
教法分析
比
较
、
探
索
(1)通过对相似三角形的回顾,引导学生对
相似三角形性质进行探索、类比,提出猜想
(2)通过“猜想——论证”的方式让学生感受知
识的形成及应用过程
(3)通过例题的变式、延伸,来培养学生的自主
探索的能力
学法指导
遵循因材施教的原则,根据学生已有的知识
水平和认知结构作出如下指导:
教学评价分析
教学目标
教师
教学内容、方法、形式、手段
(信 息 通 道)
学生
形成性练习
(反馈控制)
(信息控制)
教学流程
情景引入
课前复习
自主思考
探索新知
讲解例题
培养能力
分层练习
巩固应用
课堂小结
布置作业
探求
获取
建构
知识主线
相似三角形的性质
能力主线
训练学生思维
课前复习:
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
A
B
C
A/
B/
C/
①相似三角形的对应角_____________相等
②相似三角形的对应边______________成比例
想一想: 它们还有哪些性质呢
课前复习:
(3)相似三角形有何性质?
一个三角形有三条重要线段:
________________
如果两个三角形相似,
那么这些对应线段有什么关系呢?
情境引入
高、中线、角平分线
A
C
B
A′
B′
C′
∽
(1)
观察
A
C
B
A′
B′
C′
∽
(2)
A
C
B
A′
B′
C′
∽
(3)
∽
可得:
小结
观察这些数据,你会有怎样的猜想呢?
探索新知
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′( )
相似三角形的对应角相等
∽
( )
相似三角形的性质
探索新知
∽
所以
(相似三角形的对应边成比例)
∽
∽
相似三角形的性质
结论:相似三角形对应高的比等于相似比.
类似结论
D'
C'
B'
A'
D
C
B
A
∽
自主思考---
结论:相似三角形对应中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
类似结论
自主思考---
结论:相似三角形对应角的角平分线的比等于相似比.
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
填一填
1.相似三角形对应边的比为 2:3 那么相似比为_______,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
问题: 两个相似三角形的周长比
相似三角形的性质
会等于相似比吗?
图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
用心观察
(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______
1∶ 2
结论:相似三角形的周长比等于______.
相似比
(都相似)
2∶ 3
1∶ 2
2∶ 3
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
问题:两个相似三角形的面积
之间有什么关系呢?
相似三角形的性质
用心观察
1
2
3
1∶ 2
当相似比=k时,面积比=k2.
(1)
(2)
(3)
(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______
1∶ 4
2∶ 3
4∶ 9
相似三角形面积的比等于相似比的平方.
例5:已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高,求证:
证明:
∵△ABC∽△
∴
∴
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
面积的比等于相似比的平方
相似三角形的性质
1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.
2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.
3∶5
2:5
巩固应用
2:5
2:5
4:25
3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
(3)两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是______ ____。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。
25
10
100cm、40cm
50cm2、8cm2
4.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗
如果相似,求出△A1B1C1和△A2B2C2的面积比.
2 : 1
解:相似.
因为相似比是
所以面积比是
4 : 1
5.如图,在 ABCD中,若E是AB的中点,
则(1) AEF与 CDF的相似比为______.
(2)若 AEF的面积为5 cm2,
则 CDF的面积为______.
B
F
E
D
C
A
1 : 2
20 cm2
∵ AEF与 CDF
1:已知△ABC∽△DEF,BG、EH分别是△ABC和 △DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长。
解:∵ △ABC∽△DEF
∴ BC∶EF=BG∶EH
6∶4=4.8∶EH
EH=3.2(cm)
答:EH的长为3.2cm。
A
G
B
C
D
E
F
H
分层练习
2:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。
C'
B'
A'
C
B
A
解:因为△ABC~△A'B'C' △ABC
所以
=
=
AB
BC
A'B'
B'C'
60
72
又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米
故 AC=60–15–20=25(厘米)A'C'=72–18–24=30(厘米)
1、相似三角形对应边成____, 对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
相似多边形也有同样的结论
比例
相等
相似比
相似比
1、已知两个等边三角形的边长之比为 2 :3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?
拓展训练
拓展训练
2、平行四边形ABCD与平行四边形 相似,
已知AB=5,对应边 =6,平行四边形
ABCD的面积为10,求平行四边形
的面积.
已知△ABC∽△ ,且相似比为k。
求证:△ABC、 周长的比等于k
证明:
△ABC∽△
即△ABC、△ 的周长比等于相似比
∵
∴
∴
3、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
提高拓展
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
变式训练
4、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
(2)若AD=10,求ED的长
[板书设计]
相似三角形的性质
定理…… 例1…… 小结 (1)……
…… …… (2)……
定理…… 例2…… (3)……
…… …… (4)……
学生板演
谢谢指导
