10.3.2旋转的特征 学案 (含答案)
文档属性
| 名称 | 10.3.2旋转的特征 学案 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 19:32:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
10.3.2旋转的特征 导学案
课题 10.3.2旋转的特征 单元 第10单元 学科 数学 年级 七年级(下)
教材分析 通过具体实例认识旋转,理解旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等的性质,能够按照要求作出简单平面图形旋转后的图形.
核心素养分析 图形的旋转的特征,激发学生探究旋转的本质,加深对旋转的特征的理解.旋转的特征加以巩固,培养学生作图能力.
学习目标 1、通过具体的实例进一步认识旋转,掌握旋转的特征.2、会利用旋转的特征进行相关的证明和计算,以及画出图形经过旋转运动后形成的图形.
重点 图形的旋转的基本性质及其应用.
难点 图形的旋转的基本性质及其应用.
教学过程
课前预学 引入思考探究一: 观察教材119页图10.3.4,你能发现有哪些线段相等?有哪些角相等?探究二:1.观察教材第120页图10.3.5,你能发现有哪些线段相等?有哪些角相等?并完成下列填空: ①点A、B、C都是绕着旋转中心点O旋转 °角得到对应点A′、B′、C′,则∠AOA′= = = °② OA= ,OB= ,OC= ,③ AB= , BC= , CA= , ∠A= ,∠B= ,∠C= . ④ 旋转后的图形与原图形比较,形状大小 。 2、思考:图形旋转前后:(1)图形上每一个点的旋转方向是否相同?旋转角度是否相同?(2)对应点到旋转中心的距离有什么关系?(3)对应线段关系?对应角关系?(4)图形的形状与大小是否改变?
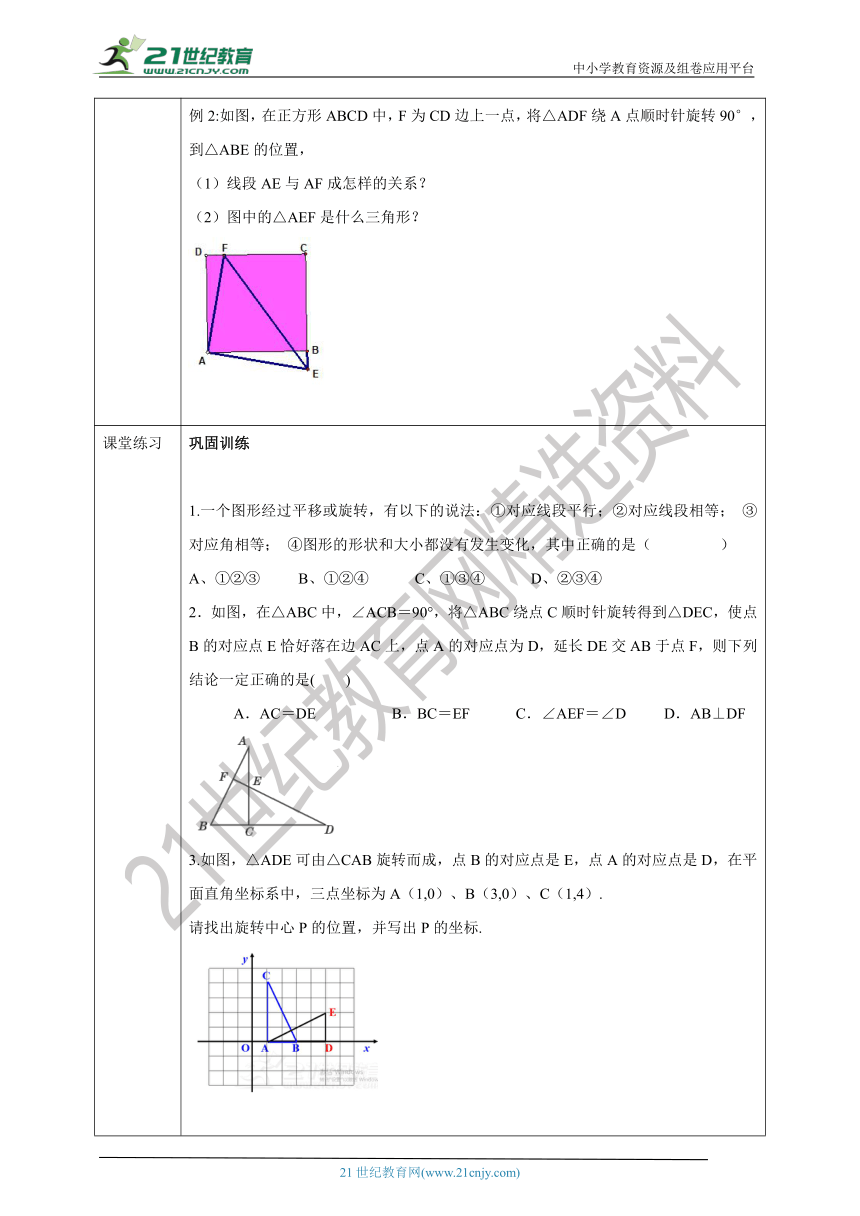
新知讲解 提炼概念旋转的特征:(1)图形中每一个点都绕着旋转中心按同一 旋转了 的角度;(2)对应点到旋转中心的距离 ;(3)对应线段 ,对应角 ;(4)图形的形状与大小 。典例精讲 例1:画△ABC绕顶点A顺时针旋转45°的图形.例2:如图,在正方形ABCD中,F为CD边上一点,将△ADF绕A点顺时针旋转90°,到△ABE的位置, (1)线段AE与AF成怎样的关系?(2)图中的△AEF是什么三角形?
课堂练习 巩固训练1.一个图形经过平移或旋转,有以下的说法:①对应线段平行;②对应线段相等; ③对应角相等; ④图形的形状和大小都没有发生变化,其中正确的是( )A、①②③ B、①②④ C、①③④ D、②③④2.如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( ) A.AC=DE B.BC=EF C.∠AEF=∠D D.AB⊥DF3.如图,△ADE可由△CAB旋转而成,点B的对应点是E,点A的对应点是D,在平面直角坐标系中,三点坐标为A(1,0)、B(3,0)、C(1,4).请找出旋转中心P的位置,并写出P的坐标.4.如图,已知∠CAE=65°,∠E=70°,且AD⊥BC,如果△ABC经过旋转后与△ADE重合.(1)旋转中心是哪个点?(2)旋转了多少度?(3)∠BAC的度数是多少?.5.如图,正方形ABCD中,E为BC边上的一点,将ΔABE旋转后得到的ΔCBF(1)指出旋转中心及旋转角度;(2)判断AE和CF的数量和位置关系;(3)如果正方形的面积是18cm2,ΔBCF的面积是5cm2,问四边形ABCD的面积是多少? 答案引入思考探究一:线段OA、OB都是绕点О逆时针旋转45°到对应线段OA'、OB',而且OA=OA', 0B =OB',AB=A'B';∠AOB = ∠A'OB',∠A=∠A',∠B=∠B'.探究二:在图10.3.5中,旋转中心是点O,点A、B、C都是绕点О逆时针旋转60°到对应点A'、B'、C',而且OA=OA',OB =OB',OC=OC';AB=A'B',BC=B'C',CA=C'A';∠CAB=∠C'A'B',∠ABC=∠A'B'C',∠BCA=∠B'C'A'.提炼概念图形旋转的特征:图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变。典例精讲 例1画法:⑴以A为顶点, AB为始边顺时针方向画∠BAB =45°,在终边上截取AB’ =AB;⑵同样画边AC , 并连结BC ;则△ABC 就是所求作的旋转图形.则△ABC 就是所求作的旋转图形.例2:解:(1)相等且互相垂直,证明如下:∵ ADF旋转后能与 BAE重合 ∴AF=AE且∠DAF=∠BAE,又∠DAF+∠FAB=90° ∴∠BAE+∠FAB=90°∴∠FAE=90°即AF⊥BE∴AF=BE 且AF⊥BE(2)由(1)可知△AEF是等腰直角三角形巩固训练1.D2.D3.P(3,2)4.解:(1)旋转中心是点A.(2)旋转的角度即为∠CAE=65°.(3)根据旋转的特征知,∠CAE=∠BAD=65°,∠C=∠E=70°.设AD⊥BC于点F.则∠AFB=90°,所以在Rt△ABF中,∠B=90°-∠BAD=25°.所以在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,即∠BAC的度数为85°.5.(1)旋转中心是点B,旋转角度是90°(2)AE=CF AE⊥CF(3)S四边形ABCD=18-5=13cm2
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
10.3.2旋转的特征 导学案
课题 10.3.2旋转的特征 单元 第10单元 学科 数学 年级 七年级(下)
教材分析 通过具体实例认识旋转,理解旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等的性质,能够按照要求作出简单平面图形旋转后的图形.
核心素养分析 图形的旋转的特征,激发学生探究旋转的本质,加深对旋转的特征的理解.旋转的特征加以巩固,培养学生作图能力.
学习目标 1、通过具体的实例进一步认识旋转,掌握旋转的特征.2、会利用旋转的特征进行相关的证明和计算,以及画出图形经过旋转运动后形成的图形.
重点 图形的旋转的基本性质及其应用.
难点 图形的旋转的基本性质及其应用.
教学过程
课前预学 引入思考探究一: 观察教材119页图10.3.4,你能发现有哪些线段相等?有哪些角相等?探究二:1.观察教材第120页图10.3.5,你能发现有哪些线段相等?有哪些角相等?并完成下列填空: ①点A、B、C都是绕着旋转中心点O旋转 °角得到对应点A′、B′、C′,则∠AOA′= = = °② OA= ,OB= ,OC= ,③ AB= , BC= , CA= , ∠A= ,∠B= ,∠C= . ④ 旋转后的图形与原图形比较,形状大小 。 2、思考:图形旋转前后:(1)图形上每一个点的旋转方向是否相同?旋转角度是否相同?(2)对应点到旋转中心的距离有什么关系?(3)对应线段关系?对应角关系?(4)图形的形状与大小是否改变?
新知讲解 提炼概念旋转的特征:(1)图形中每一个点都绕着旋转中心按同一 旋转了 的角度;(2)对应点到旋转中心的距离 ;(3)对应线段 ,对应角 ;(4)图形的形状与大小 。典例精讲 例1:画△ABC绕顶点A顺时针旋转45°的图形.例2:如图,在正方形ABCD中,F为CD边上一点,将△ADF绕A点顺时针旋转90°,到△ABE的位置, (1)线段AE与AF成怎样的关系?(2)图中的△AEF是什么三角形?
课堂练习 巩固训练1.一个图形经过平移或旋转,有以下的说法:①对应线段平行;②对应线段相等; ③对应角相等; ④图形的形状和大小都没有发生变化,其中正确的是( )A、①②③ B、①②④ C、①③④ D、②③④2.如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( ) A.AC=DE B.BC=EF C.∠AEF=∠D D.AB⊥DF3.如图,△ADE可由△CAB旋转而成,点B的对应点是E,点A的对应点是D,在平面直角坐标系中,三点坐标为A(1,0)、B(3,0)、C(1,4).请找出旋转中心P的位置,并写出P的坐标.4.如图,已知∠CAE=65°,∠E=70°,且AD⊥BC,如果△ABC经过旋转后与△ADE重合.(1)旋转中心是哪个点?(2)旋转了多少度?(3)∠BAC的度数是多少?.5.如图,正方形ABCD中,E为BC边上的一点,将ΔABE旋转后得到的ΔCBF(1)指出旋转中心及旋转角度;(2)判断AE和CF的数量和位置关系;(3)如果正方形的面积是18cm2,ΔBCF的面积是5cm2,问四边形ABCD的面积是多少? 答案引入思考探究一:线段OA、OB都是绕点О逆时针旋转45°到对应线段OA'、OB',而且OA=OA', 0B =OB',AB=A'B';∠AOB = ∠A'OB',∠A=∠A',∠B=∠B'.探究二:在图10.3.5中,旋转中心是点O,点A、B、C都是绕点О逆时针旋转60°到对应点A'、B'、C',而且OA=OA',OB =OB',OC=OC';AB=A'B',BC=B'C',CA=C'A';∠CAB=∠C'A'B',∠ABC=∠A'B'C',∠BCA=∠B'C'A'.提炼概念图形旋转的特征:图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变。典例精讲 例1画法:⑴以A为顶点, AB为始边顺时针方向画∠BAB =45°,在终边上截取AB’ =AB;⑵同样画边AC , 并连结BC ;则△ABC 就是所求作的旋转图形.则△ABC 就是所求作的旋转图形.例2:解:(1)相等且互相垂直,证明如下:∵ ADF旋转后能与 BAE重合 ∴AF=AE且∠DAF=∠BAE,又∠DAF+∠FAB=90° ∴∠BAE+∠FAB=90°∴∠FAE=90°即AF⊥BE∴AF=BE 且AF⊥BE(2)由(1)可知△AEF是等腰直角三角形巩固训练1.D2.D3.P(3,2)4.解:(1)旋转中心是点A.(2)旋转的角度即为∠CAE=65°.(3)根据旋转的特征知,∠CAE=∠BAD=65°,∠C=∠E=70°.设AD⊥BC于点F.则∠AFB=90°,所以在Rt△ABF中,∠B=90°-∠BAD=25°.所以在△ABC中,∠BAC=180°-∠B-∠C=180°-25°-70°=85°,即∠BAC的度数为85°.5.(1)旋转中心是点B,旋转角度是90°(2)AE=CF AE⊥CF(3)S四边形ABCD=18-5=13cm2
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
