九年级数学上册试题 4.3 相似多边形 -北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.3 相似多边形 -北师大版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 16:26:15 | ||
图片预览

文档简介
4.3 相似多边形
第一课时
一、单选题
1.下列说法正确的有( ).
①形状差不多的两个图形相似;②国旗上的大五角星与小五角星是相似的;③大小不等的两个六边形的形状可能相似;④放大镜下看到的图形与原来的图形的相似.
A.1个 B.2个 C.3个 D.4个
2.下列多边形一定相似的是( )
A.两个平行四边形 B.两个矩形
C.两个菱形 D.两个正方形
3.两个相似六边形,若对应边之比为3:2,则这两个六边形的周长比为( )
A.9:4 B.9:2 C.3:1 D.3:2
4.如图,正五边形与正五边形相似,若,则下列结论正确的是( )
A. B. C. D.
5.将一张矩形纸片对折后裁下,得到两张大小完全一样的矩形纸片,已知它们都与原来的矩形相似,那么原来矩形长与宽的比为( )
A.2:1 B.:1 C.3:1 D.:1
6.下列各组图形中,不一定相似的是( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
7.如果五边形ABCDE∽五边形POGMN且对应高之比为3:2,那么五边形ABCDE和五边形POGMN的面积之比是( )
A.2:3 B.3:2 C.6:4 D.9:4
8.在如图所示的三个矩形中,相似的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.甲、乙和丙
9.如图,在四边形ABCD中,∠A=∠B=90°,点F为边CD上一点,且FE⊥AB交AB于点E,若AD=2,BC=8,四边形AEFD~四边形EBCF,则的值是( )
A. B. C. D.
10.如图,点O是四边形ABCD内一点,、、、分别是OA、OB、OC、OD上的点,且,若四边形的面积为12cm2,则四边形ABCD的面积为( )
A.18cm2 B.27cm2 C.36cm2 D.54cm2
二、填空题
11.下列命题中,正确命题的个数为________.
①所有的正方形都相似
②所有的菱形都相似
③边长相等的两个菱形都相似
④对角线相等的两个矩形都相似
12.如图所示的两个五边形相似,则_____,______,_______,______.
13.若两个相似多边形的对应边之比为5:2,则它们的周长比是______,面积比是______.
14.若四边形与四边形相似,与,与分别是对应边,,则________.
15.如图,四边形四边形,若,则________.
16.有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab= ___cm2
17.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=_____.
18.小颖在一本书上看到一个风筝模型,形状如图所示,其中对角线,并且两条对角线长分别为和.现在小颖照着模型按照1:3的比例放大制作一个大风筝,制作风筝需要彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是_________.
三、解答题
19.如图,四边形ABCD∽四边形EFGH,求角α、β的大小和EH的长度x.
20.网格中每个小正方形的边长为1,每个小正方形的顶点为格点,三角形和长方形的顶点都在格点上.
(1)在图1的网格中按2:1画出网格中三角形放大后的图形①;
(2)在图2的网格中按1:2画出网格中长方形缩小后的图形②;
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 .
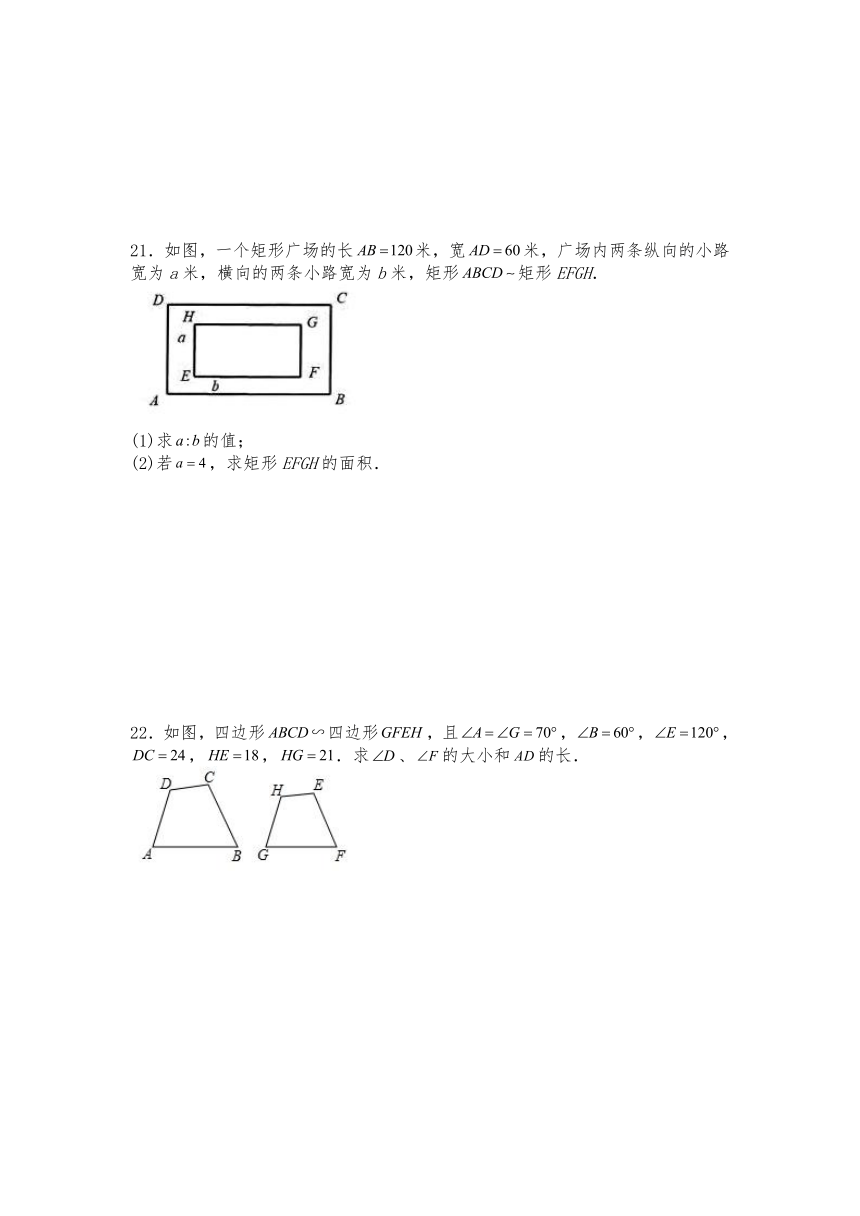
21.如图,一个矩形广场的长米,宽米,广场内两条纵向的小路宽为a米,横向的两条小路宽为b米,矩形矩形EFGH.
(1)求的值;
(2)若,求矩形EFGH的面积.
22.如图,四边形四边形,且,,,,,.求、的大小和的长.
第二课时
一、单选题
1.如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到的两个矩形都与原矩形相似,则原矩形长与宽的比是( )
A.2:1 B.1:2
C.3:2 D.:1
2.如图,矩形矩形,连结,延长分别交、于点、,延长、交于点,一定能求出面积的条件是( )
A.矩形和矩形的面积之差 B.矩形和矩形的面积之差
C.矩形和矩形的面积之差 D.矩形和矩形的面积之差
3.如图,一块矩形纸片,长为20cm,宽为15cm,现在把这个矩形纸片的左右同时剪去宽为cm的纸条、上下同时剪去宽为cm的纸条(如图所示的阴影部分),要使剩下的矩形与原来的矩形相似,则与满足的关系式为( )
A. B. C. D.
4.如图,矩形的四个顶点分别在菱形的四条边上,.将,分别沿边,折叠,当重叠部分为菱形且面积是菱形面积的时,则为( )
A. B.2 C. D.
5.甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
6.如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1四边的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为( )
A. B. C. D.
7.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为( )
A. B. C. D.
8.如图,在矩形ABCD中,,,连接AC,以对角线AC为边,按逆时针方向作矩形,使矩形矩形ADCB;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,…,按照此规律作下去,则边的长为( )
A. B. C. D.
二、填空题
9.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽,以AB为长的矩形面积为S2,S1______S2(填“”或“”或“”).
10.把正方形ABCD沿对角线AC的方向移动到A1B1C1D1的位置,它们重叠部分的面积是正方形ABCD的面积的一半,若AC=,则平移的距离是________.
11.将图1中的矩形和正方形纸片沿图2中的虚线剪成5块,再用这5块拼接成如图3所示矩形,其中阴影部分为空余部分,若AB=2AD,则的值为________.
12.我们通常用到的一种复印纸,整张称为纸(如图),按下图方式对折一分为二裁开成为纸(如图),再一分为二成为纸(如图)…它们都是相似的矩形,这些矩形的长与宽的比值都是一定值,这个定值是________.
13.如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是_____.
14.已知菱形的边长为2,=60°,对角线,相交于点O.以点O为坐标原点,分别以,所在直线为x轴、y轴,建立如图所示的直角坐标系.以为对角线作菱形∽菱形,再以为对角线作菱形∽菱形,再以为对角线作菱形∽菱形, ,按此规律继续作下去,在x轴的正半轴上得到点,,,......,,则点的坐标为________.
三、解答题
15.如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2﹣4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
16.(1)定义1:若一个矩形的周长和面积分别是另一个矩形周长和面积的2倍,则称这个矩形是原矩形的“加倍矩形”
问题1:一个正方形是否存在一个“加倍正方形”?答______(填“是”或“否”);
问题2:长为3,宽为1的矩形的“加倍矩形”的长为______,宽为______;
(2)定义2:若一个矩形的周长和面积分别是另一个矩形周长和面积的,则称这个矩形是原矩形的“减半矩形”.
问题3:长为4,宽为1的矩形的“减半矩形”是否存在?答______(填“是”或“否”);
问题4:长为6,宽为1的矩形的“减半矩形”的长为______;
问题5:长为n,宽为1的矩形的“加倍矩形”的长为______;(用n的代数式表示)
问题6:长为n,宽为1的矩形的“减半矩形”的存在条件是______;(用含n的关系式表示)
(3)定义3:若一个矩形的周长和面积分别是另一个矩形周长和面积的k倍,则称这个矩形是原矩形的“k倍矩形”(注意,且k可以取小于1的数)
问题7:长为n,宽为1的矩形的“k倍矩形”的存在条件是______;(、,用含n、k的关系式表示)
17.下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m的空地,其他三侧内墙各保留1 m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288 m2
解:设矩形蔬菜种植区域的宽为x_m,则长为2xm,
根据题意,得x·2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12,
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28 m,宽为14 m时,矩形蔬菜种植区域的面积是288 m2.
我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样?
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
第一课时答案
一、单选题
C.D.D.B.B.D.D.A.B.B.
二、填空题
11.1.
12.a=3,b=4.5,c=4,d=6.
13.5:2;25:4.
14..
15.103.
16.54.
17.
18.540
三、解答题
19.解:∵四边形ABCD∽四边形EFGH,
∴α=∠C=83°,∠F=∠B=78°,EH:AD=EF:AB,
∴x:21=24:18,解得x=28.
在四边形EFGH中,β=360°﹣83°﹣78°﹣118°=81°.
∴∠G=∠C=67°.
故x=28.
20.(1)
解:如图1,①即为所求.
(2)
解:如图2,②即为所求.
(3)
解:①的面积:
②的面积:
面积比:18:8=9:4
∴图形①的面积与图形②的面积最简整数比为9:4.
故答案为:9:4.
21.(1)
根据题意可知:HE=(60﹣2b)米,EF=(120﹣2a)米,
∵矩形ABCD∽矩形EFGH.
∴,
∴,
整理,得2b=a,
∴a:b=2:1;
(2)
∵a=4,2b=a,
∴b=2,
∴矩形EFGH的面积
=EF HE
=(120﹣2a) (60﹣2b)
=(120﹣8)(60﹣4)
=112×56
=6272(米2).
答:矩形EFGH的面积为6272米2.
22.解:∵四边形四边形,
∴,
又∵,
∴,
∵四边形四边形,
∴,∵,,
∴,解得.
∴.
第二课时答案
一、单选题
D.B.D.D.C.C.D.A.
二、填空题
9.=
10.-1.
11..
12..
13..
14.(3n-1,0).
三、解答题
15.∵相似五边形的面积比是1:4,
∴它们的相似比为1:2,
即(x2﹣4):(x2+2x)=1:2,
整理得x2﹣2x﹣8=0,解得x1=4,x2=﹣2(舍去),
当x=4时,x2﹣4=12,x2+2x=24,
∴这根铁丝的总长=5×12+5×24=180(cm).
16.解:(1)问题1:不存在.
因为两个正方形是相似图形,当它们的周长比为2时,则面积比必定是4,所以不存在.
问题2:设“加倍矩形”的长和宽分别为x,y.则:,解得(舍去).
故答案为:,;
(2)问题3:设“减半矩形”的长和宽分别为m,c.则:,消元并化简得,;
∵,
∴方程没有实数根,故不存在;
故答案为:否;
问题4:设“减半矩形”的长和宽分别为a,b.则:,
解得,或(舍去);
故答案为:2;
问题5:设“加倍矩形”的长和宽分别为d,e.则:,解得或(舍去);
故答案为:;
问题6:设“减半矩形”的长和宽分别为f,g.则:,消元并化简得,;
∵,
解得, 或
故答案为: 或;
(3)问题7:设“k倍矩形”的长和宽分别为t,s.则:,消元并化简得,;
∵,
解得,
故答案为:;
17.解 (1)小明没有说明矩形蔬菜种植区域的长与宽之比为2∶1的理由.
在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:
设温室的宽为xm,则长为2xm.
则矩形蔬菜种植区域的宽为(x-1-1)m,长为(2x-3-1)m.
∵==2,
∴矩形蔬菜种植区域的长与宽之比为2∶1;
(2)要使矩形A′B′C′D′∽矩形ABCD,
就要=,即=,
即=,
即2AB-2(b+d)=2AB-(a+c),
∴a+c=2(b+d),
=2.
第一课时
一、单选题
1.下列说法正确的有( ).
①形状差不多的两个图形相似;②国旗上的大五角星与小五角星是相似的;③大小不等的两个六边形的形状可能相似;④放大镜下看到的图形与原来的图形的相似.
A.1个 B.2个 C.3个 D.4个
2.下列多边形一定相似的是( )
A.两个平行四边形 B.两个矩形
C.两个菱形 D.两个正方形
3.两个相似六边形,若对应边之比为3:2,则这两个六边形的周长比为( )
A.9:4 B.9:2 C.3:1 D.3:2
4.如图,正五边形与正五边形相似,若,则下列结论正确的是( )
A. B. C. D.
5.将一张矩形纸片对折后裁下,得到两张大小完全一样的矩形纸片,已知它们都与原来的矩形相似,那么原来矩形长与宽的比为( )
A.2:1 B.:1 C.3:1 D.:1
6.下列各组图形中,不一定相似的是( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
7.如果五边形ABCDE∽五边形POGMN且对应高之比为3:2,那么五边形ABCDE和五边形POGMN的面积之比是( )
A.2:3 B.3:2 C.6:4 D.9:4
8.在如图所示的三个矩形中,相似的是( )
A.甲和乙 B.甲和丙 C.乙和丙 D.甲、乙和丙
9.如图,在四边形ABCD中,∠A=∠B=90°,点F为边CD上一点,且FE⊥AB交AB于点E,若AD=2,BC=8,四边形AEFD~四边形EBCF,则的值是( )
A. B. C. D.
10.如图,点O是四边形ABCD内一点,、、、分别是OA、OB、OC、OD上的点,且,若四边形的面积为12cm2,则四边形ABCD的面积为( )
A.18cm2 B.27cm2 C.36cm2 D.54cm2
二、填空题
11.下列命题中,正确命题的个数为________.
①所有的正方形都相似
②所有的菱形都相似
③边长相等的两个菱形都相似
④对角线相等的两个矩形都相似
12.如图所示的两个五边形相似,则_____,______,_______,______.
13.若两个相似多边形的对应边之比为5:2,则它们的周长比是______,面积比是______.
14.若四边形与四边形相似,与,与分别是对应边,,则________.
15.如图,四边形四边形,若,则________.
16.有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab= ___cm2
17.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=_____.
18.小颖在一本书上看到一个风筝模型,形状如图所示,其中对角线,并且两条对角线长分别为和.现在小颖照着模型按照1:3的比例放大制作一个大风筝,制作风筝需要彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是_________.
三、解答题
19.如图,四边形ABCD∽四边形EFGH,求角α、β的大小和EH的长度x.
20.网格中每个小正方形的边长为1,每个小正方形的顶点为格点,三角形和长方形的顶点都在格点上.
(1)在图1的网格中按2:1画出网格中三角形放大后的图形①;
(2)在图2的网格中按1:2画出网格中长方形缩小后的图形②;
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 .
21.如图,一个矩形广场的长米,宽米,广场内两条纵向的小路宽为a米,横向的两条小路宽为b米,矩形矩形EFGH.
(1)求的值;
(2)若,求矩形EFGH的面积.
22.如图,四边形四边形,且,,,,,.求、的大小和的长.
第二课时
一、单选题
1.如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到的两个矩形都与原矩形相似,则原矩形长与宽的比是( )
A.2:1 B.1:2
C.3:2 D.:1
2.如图,矩形矩形,连结,延长分别交、于点、,延长、交于点,一定能求出面积的条件是( )
A.矩形和矩形的面积之差 B.矩形和矩形的面积之差
C.矩形和矩形的面积之差 D.矩形和矩形的面积之差
3.如图,一块矩形纸片,长为20cm,宽为15cm,现在把这个矩形纸片的左右同时剪去宽为cm的纸条、上下同时剪去宽为cm的纸条(如图所示的阴影部分),要使剩下的矩形与原来的矩形相似,则与满足的关系式为( )
A. B. C. D.
4.如图,矩形的四个顶点分别在菱形的四条边上,.将,分别沿边,折叠,当重叠部分为菱形且面积是菱形面积的时,则为( )
A. B.2 C. D.
5.甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
6.如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1四边的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为( )
A. B. C. D.
7.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为( )
A. B. C. D.
8.如图,在矩形ABCD中,,,连接AC,以对角线AC为边,按逆时针方向作矩形,使矩形矩形ADCB;再连接,以对角线为边,按逆时针方向作矩形,使矩形矩形,…,按照此规律作下去,则边的长为( )
A. B. C. D.
二、填空题
9.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽,以AB为长的矩形面积为S2,S1______S2(填“”或“”或“”).
10.把正方形ABCD沿对角线AC的方向移动到A1B1C1D1的位置,它们重叠部分的面积是正方形ABCD的面积的一半,若AC=,则平移的距离是________.
11.将图1中的矩形和正方形纸片沿图2中的虚线剪成5块,再用这5块拼接成如图3所示矩形,其中阴影部分为空余部分,若AB=2AD,则的值为________.
12.我们通常用到的一种复印纸,整张称为纸(如图),按下图方式对折一分为二裁开成为纸(如图),再一分为二成为纸(如图)…它们都是相似的矩形,这些矩形的长与宽的比值都是一定值,这个定值是________.
13.如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是_____.
14.已知菱形的边长为2,=60°,对角线,相交于点O.以点O为坐标原点,分别以,所在直线为x轴、y轴,建立如图所示的直角坐标系.以为对角线作菱形∽菱形,再以为对角线作菱形∽菱形,再以为对角线作菱形∽菱形, ,按此规律继续作下去,在x轴的正半轴上得到点,,,......,,则点的坐标为________.
三、解答题
15.如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2﹣4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
16.(1)定义1:若一个矩形的周长和面积分别是另一个矩形周长和面积的2倍,则称这个矩形是原矩形的“加倍矩形”
问题1:一个正方形是否存在一个“加倍正方形”?答______(填“是”或“否”);
问题2:长为3,宽为1的矩形的“加倍矩形”的长为______,宽为______;
(2)定义2:若一个矩形的周长和面积分别是另一个矩形周长和面积的,则称这个矩形是原矩形的“减半矩形”.
问题3:长为4,宽为1的矩形的“减半矩形”是否存在?答______(填“是”或“否”);
问题4:长为6,宽为1的矩形的“减半矩形”的长为______;
问题5:长为n,宽为1的矩形的“加倍矩形”的长为______;(用n的代数式表示)
问题6:长为n,宽为1的矩形的“减半矩形”的存在条件是______;(用含n的关系式表示)
(3)定义3:若一个矩形的周长和面积分别是另一个矩形周长和面积的k倍,则称这个矩形是原矩形的“k倍矩形”(注意,且k可以取小于1的数)
问题7:长为n,宽为1的矩形的“k倍矩形”的存在条件是______;(、,用含n、k的关系式表示)
17.下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m的空地,其他三侧内墙各保留1 m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288 m2
解:设矩形蔬菜种植区域的宽为x_m,则长为2xm,
根据题意,得x·2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12,
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28 m,宽为14 m时,矩形蔬菜种植区域的面积是288 m2.
我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?
(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样?
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
第一课时答案
一、单选题
C.D.D.B.B.D.D.A.B.B.
二、填空题
11.1.
12.a=3,b=4.5,c=4,d=6.
13.5:2;25:4.
14..
15.103.
16.54.
17.
18.540
三、解答题
19.解:∵四边形ABCD∽四边形EFGH,
∴α=∠C=83°,∠F=∠B=78°,EH:AD=EF:AB,
∴x:21=24:18,解得x=28.
在四边形EFGH中,β=360°﹣83°﹣78°﹣118°=81°.
∴∠G=∠C=67°.
故x=28.
20.(1)
解:如图1,①即为所求.
(2)
解:如图2,②即为所求.
(3)
解:①的面积:
②的面积:
面积比:18:8=9:4
∴图形①的面积与图形②的面积最简整数比为9:4.
故答案为:9:4.
21.(1)
根据题意可知:HE=(60﹣2b)米,EF=(120﹣2a)米,
∵矩形ABCD∽矩形EFGH.
∴,
∴,
整理,得2b=a,
∴a:b=2:1;
(2)
∵a=4,2b=a,
∴b=2,
∴矩形EFGH的面积
=EF HE
=(120﹣2a) (60﹣2b)
=(120﹣8)(60﹣4)
=112×56
=6272(米2).
答:矩形EFGH的面积为6272米2.
22.解:∵四边形四边形,
∴,
又∵,
∴,
∵四边形四边形,
∴,∵,,
∴,解得.
∴.
第二课时答案
一、单选题
D.B.D.D.C.C.D.A.
二、填空题
9.=
10.-1.
11..
12..
13..
14.(3n-1,0).
三、解答题
15.∵相似五边形的面积比是1:4,
∴它们的相似比为1:2,
即(x2﹣4):(x2+2x)=1:2,
整理得x2﹣2x﹣8=0,解得x1=4,x2=﹣2(舍去),
当x=4时,x2﹣4=12,x2+2x=24,
∴这根铁丝的总长=5×12+5×24=180(cm).
16.解:(1)问题1:不存在.
因为两个正方形是相似图形,当它们的周长比为2时,则面积比必定是4,所以不存在.
问题2:设“加倍矩形”的长和宽分别为x,y.则:,解得(舍去).
故答案为:,;
(2)问题3:设“减半矩形”的长和宽分别为m,c.则:,消元并化简得,;
∵,
∴方程没有实数根,故不存在;
故答案为:否;
问题4:设“减半矩形”的长和宽分别为a,b.则:,
解得,或(舍去);
故答案为:2;
问题5:设“加倍矩形”的长和宽分别为d,e.则:,解得或(舍去);
故答案为:;
问题6:设“减半矩形”的长和宽分别为f,g.则:,消元并化简得,;
∵,
解得, 或
故答案为: 或;
(3)问题7:设“k倍矩形”的长和宽分别为t,s.则:,消元并化简得,;
∵,
解得,
故答案为:;
17.解 (1)小明没有说明矩形蔬菜种植区域的长与宽之比为2∶1的理由.
在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:
设温室的宽为xm,则长为2xm.
则矩形蔬菜种植区域的宽为(x-1-1)m,长为(2x-3-1)m.
∵==2,
∴矩形蔬菜种植区域的长与宽之比为2∶1;
(2)要使矩形A′B′C′D′∽矩形ABCD,
就要=,即=,
即=,
即2AB-2(b+d)=2AB-(a+c),
∴a+c=2(b+d),
=2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
