九年级数学上册试题 第六章反比例函数单元卷-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 第六章反比例函数单元卷-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 17:16:13 | ||
图片预览



文档简介
第六章反比例函数单元卷
一、选择题(12小题,每小题3分,共36分)
1.当x>0时,函数y=的图象在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.下列函数中,y是x的反比例函数的是( )
A.y=2x B.y= C.y=x+3 D.y=x2
3.在平面直角坐标系中,反比例函数的图象位于( )
A.第二、四象限 B.第一、三象限
C.第一、四象限 D.第三、四象限
4.已知点P(﹣3,2)是反比例函数图象上的一点,则该反比例函数的表达式为( )
A.y= B.y=﹣ C.y= D.y=﹣
5.反比例函数y=(a﹣1)xa的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
6.已知反比例函数y=﹣的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是( )
A.y1<y2<0 B.0<y2<y1 C.y1<0<y2 D.y2<0<y1
7.如图,平行四边形ABOC中,对角线交于点E,双曲线y=经过C、E两点,若平行四边形ABOC的面积为10,则k的值是( )
A.﹣ B.﹣ C.﹣4 D.﹣5
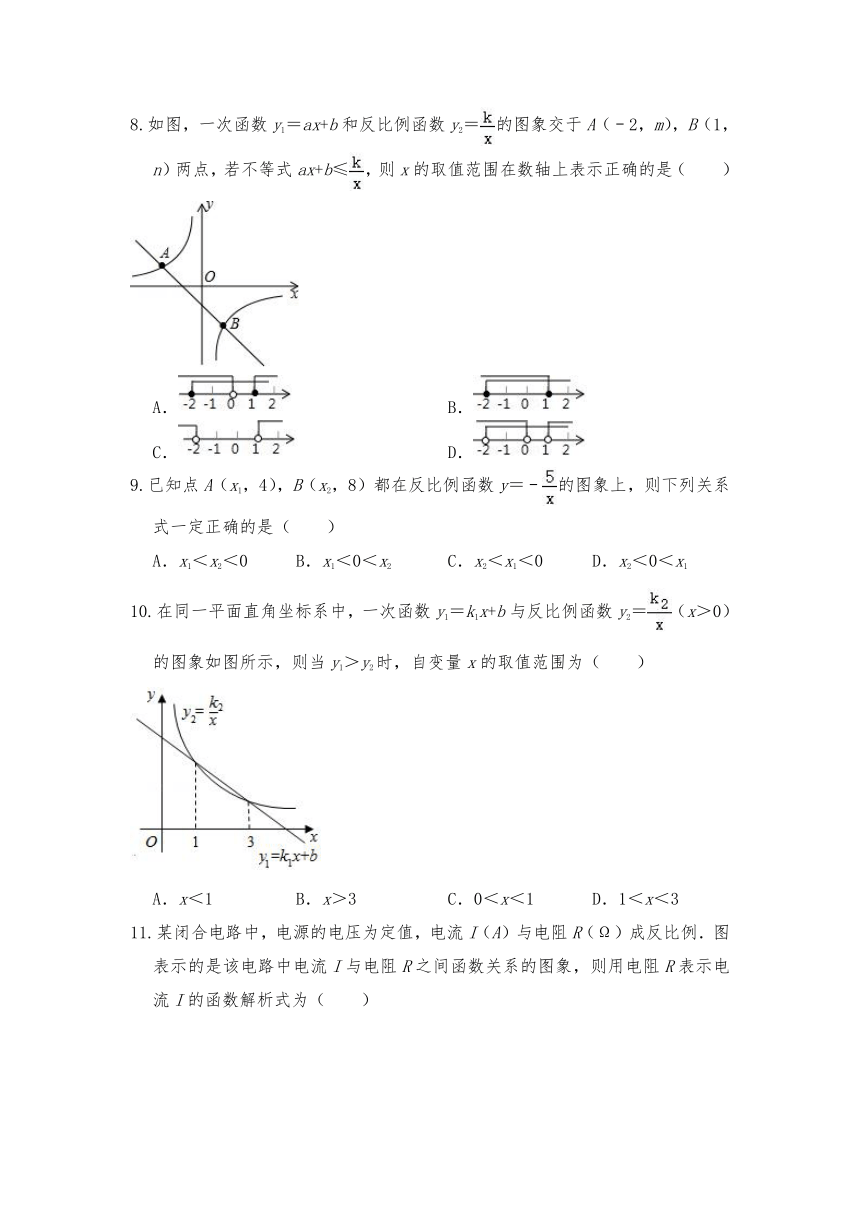
8.如图,一次函数y1=ax+b和反比例函数y2=的图象交于A(﹣2,m),B(1,n)两点,若不等式ax+b≤,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
9.已知点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,则下列关系式一定正确的是( )
A.x1<x2<0 B.x1<0<x2 C.x2<x1<0 D.x2<0<x1
10.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( )
A.x<1 B.x>3 C.0<x<1 D.1<x<3
11.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为( )
A. B. C. D.
12.教室里的饮水机接通电源就进入自动程序,开机加热每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.水温y(℃)和时间x(min)的关系如图.某天张老师在水温为30℃时,接通了电源,为了在上午课间时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:50 B.7:45 C.7:30 D.7:20
二、填空题(4小题,每小题3分,共12分)
13.当m 时,函数y=的图象在第二、四象限内.
14.若A(7,y1),B(5,y2),都是反比例函数y=的图象上的点,则y1 y2(填“<”、”﹣”或”>”).
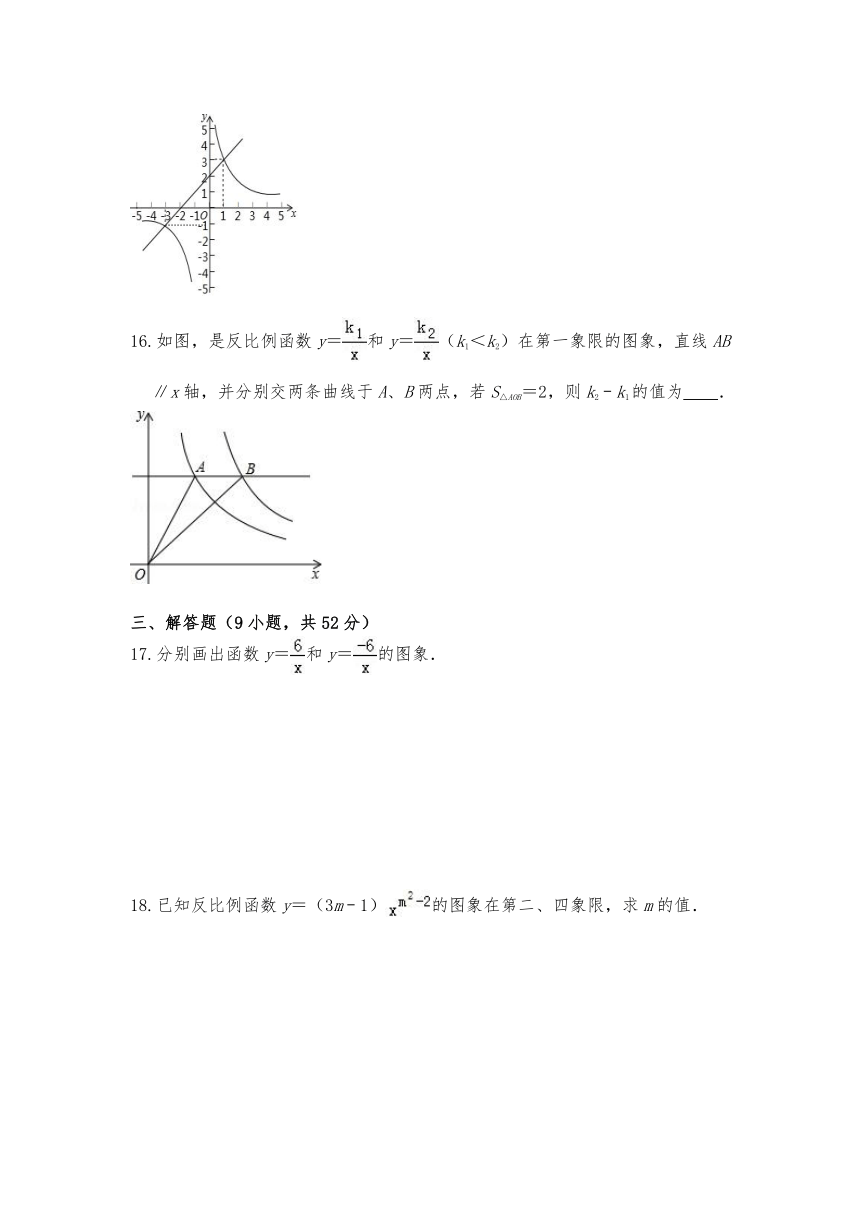
15.两个函数y=ax+b和y=(abc≠0)的图象如图所示,请直接写出关于x的不等式ax+b>的解集 ﹣ .
16.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=2,则k2﹣k1的值为 .
三、解答题(9小题,共52分)
17.分别画出函数y=和y=的图象.
18.已知反比例函数y=(3m﹣1)的图象在第二、四象限,求m的值.
19.已知y=y1+y2,其中y1与x2成正比例,y2与x成反比例,并且当x=时y=5,当x=1时y=﹣1,求y与x之间的函数关系式.
20.反比例函数y=与一次函数y=2x﹣4的图象都过A(m,2).
(1)求A点坐标;
(2)求反比例函数解析式.
21.已知反比例函数y=(k≠0)的图象经过点A(2,3).
(1)求函数解析式;
(2)当x=﹣4时,求反比例函数y=的值.
22.已知矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm).
(1)写出y与x之间的函数关系式.并求出自变量的取值范围.
(2)画出这个函数的图象.
23.如图,点A与点B在反比例函数y=(x>0)的图象上,A点的纵坐标为2,BB′与AA′均垂直于x轴,B′,A′是垂足.
(1)求A点的坐标;
(2)求△BOB′的面积;
(3)若B点的横坐标为2,求△OAB的面积.
24.(1)你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y cm是面条粗细(横截面积)xcm2的反比例函数.假设它的图象如图所示,则y与x的函数表达式为 .
(2)一种新型汽车可装汽油500L,若汽车每小时用油量为x L.
①用油时间y h与每小时的用油量x L之间的函数表达式可表示为 ;
②每小时的用油量为25L,则这些油可用的时间为 ;
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围是 .
25.一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形的长x(cm)与宽y(cm)之间的函数关系如图2所示:
(1)求y与x之间的函数关系式;
(2)“E”图案的面积是多少?
(3)如果小矩形的长是6≤x≤12cm,求小矩形宽的范围.
答案
一、选择题
D.B.B.D.B.D.B.A.A.D.C.D.
二、填空题
13.1.
14.<.
15.﹣3<x<0或x>1.
16.4.
三、解答题
17.解:①列表:
②描点:把表中的对应的数值作为点的坐标在坐标系中描出来,
③连线:用平滑的线顺次连起来.
18.解:∵反比例函数y=(3m﹣1)的图象在第二、四象限,
∴m2﹣2=﹣1,3m﹣1<0,
∴m=﹣1.
19.解:∵y1与x2成正比例,y2与x成反比例,
∴y1=kx2,y2=,
∵y=y1+y2,
∴y=kx2+,
∵当x=时y=5,当x=1时y=﹣1,
∴,
解得:,
∴y与x之间的函数关系式为y=﹣4x2+.
20.解:(1)将点A(m,2)代入y=2x﹣4得:
2m﹣4=2,
解得:m=3,
∴点A的坐标为(3,2);
(2)将点A(3,2)代入y=得:k=6,
∴反比例函数解析式为y=.
21.解:(1)把A(2,3)代入y=得k=2×3=6,
所以反比例函数解析式为y=;
(2)当x=﹣4时,y==﹣=﹣.
22.解:(1)∵矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm),
∴xy=6,
故y与x之间的函数关系式为:y=,自变量的取值范围是:x>0;
(2)如图所示:
.
23.解:(1)当y=2时,则x==4.即点A的坐标是(4,2);
(2)S△BOB'=×8=4;
(3)在y=中,当x=2时,y==4,则B的坐标是(2,4),
根据反比例函数的解析式,知三角形OAA1的面积和三角形OBB1的面积相等,都是4,
则直角梯形ABB1A1的面积是×(2+4)×2=6.
24.解:(1)设反比例函数图象的解析式为y=,
由图得,反比例函数上一点坐标为(0.04,3200)代入y=,有k=0.04×3200=128,
又题中实际意义需x>0.
∴y=(x>0).
(2)①∵可装汽油500L,若汽车每小时用油量为xL,
∴用油时间yh与每小时的用油量xL之间的函数表达式可表示为y=;
②每小时的用油量为25L,则这些油可用的时间为500÷25=20小时;
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围0≤x<10;
故答案为:y=(x>0).y=;20;0≤x<10;
25.解:(1)设函数关系式为,
∵函数图象经过(10,2)
∴
∴k=20,
∴
∵0<x<16,0<y<8,
∴0<x<16,0<<8,
∴<x<16;
(2)∵
∴xy=20,
∴SE=S正=162﹣2×20=216;
(3)当x=6时,,
当x=12时,,
∴小矩形的长是6≤x≤12cm,小矩形宽的范围为.
一、选择题(12小题,每小题3分,共36分)
1.当x>0时,函数y=的图象在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.下列函数中,y是x的反比例函数的是( )
A.y=2x B.y= C.y=x+3 D.y=x2
3.在平面直角坐标系中,反比例函数的图象位于( )
A.第二、四象限 B.第一、三象限
C.第一、四象限 D.第三、四象限
4.已知点P(﹣3,2)是反比例函数图象上的一点,则该反比例函数的表达式为( )
A.y= B.y=﹣ C.y= D.y=﹣
5.反比例函数y=(a﹣1)xa的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
6.已知反比例函数y=﹣的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是( )
A.y1<y2<0 B.0<y2<y1 C.y1<0<y2 D.y2<0<y1
7.如图,平行四边形ABOC中,对角线交于点E,双曲线y=经过C、E两点,若平行四边形ABOC的面积为10,则k的值是( )
A.﹣ B.﹣ C.﹣4 D.﹣5
8.如图,一次函数y1=ax+b和反比例函数y2=的图象交于A(﹣2,m),B(1,n)两点,若不等式ax+b≤,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
9.已知点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,则下列关系式一定正确的是( )
A.x1<x2<0 B.x1<0<x2 C.x2<x1<0 D.x2<0<x1
10.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( )
A.x<1 B.x>3 C.0<x<1 D.1<x<3
11.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为( )
A. B. C. D.
12.教室里的饮水机接通电源就进入自动程序,开机加热每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.水温y(℃)和时间x(min)的关系如图.某天张老师在水温为30℃时,接通了电源,为了在上午课间时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:50 B.7:45 C.7:30 D.7:20
二、填空题(4小题,每小题3分,共12分)
13.当m 时,函数y=的图象在第二、四象限内.
14.若A(7,y1),B(5,y2),都是反比例函数y=的图象上的点,则y1 y2(填“<”、”﹣”或”>”).
15.两个函数y=ax+b和y=(abc≠0)的图象如图所示,请直接写出关于x的不等式ax+b>的解集 ﹣ .
16.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=2,则k2﹣k1的值为 .
三、解答题(9小题,共52分)
17.分别画出函数y=和y=的图象.
18.已知反比例函数y=(3m﹣1)的图象在第二、四象限,求m的值.
19.已知y=y1+y2,其中y1与x2成正比例,y2与x成反比例,并且当x=时y=5,当x=1时y=﹣1,求y与x之间的函数关系式.
20.反比例函数y=与一次函数y=2x﹣4的图象都过A(m,2).
(1)求A点坐标;
(2)求反比例函数解析式.
21.已知反比例函数y=(k≠0)的图象经过点A(2,3).
(1)求函数解析式;
(2)当x=﹣4时,求反比例函数y=的值.
22.已知矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm).
(1)写出y与x之间的函数关系式.并求出自变量的取值范围.
(2)画出这个函数的图象.
23.如图,点A与点B在反比例函数y=(x>0)的图象上,A点的纵坐标为2,BB′与AA′均垂直于x轴,B′,A′是垂足.
(1)求A点的坐标;
(2)求△BOB′的面积;
(3)若B点的横坐标为2,求△OAB的面积.
24.(1)你吃过兰州拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y cm是面条粗细(横截面积)xcm2的反比例函数.假设它的图象如图所示,则y与x的函数表达式为 .
(2)一种新型汽车可装汽油500L,若汽车每小时用油量为x L.
①用油时间y h与每小时的用油量x L之间的函数表达式可表示为 ;
②每小时的用油量为25L,则这些油可用的时间为 ;
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围是 .
25.一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形的长x(cm)与宽y(cm)之间的函数关系如图2所示:
(1)求y与x之间的函数关系式;
(2)“E”图案的面积是多少?
(3)如果小矩形的长是6≤x≤12cm,求小矩形宽的范围.
答案
一、选择题
D.B.B.D.B.D.B.A.A.D.C.D.
二、填空题
13.1.
14.<.
15.﹣3<x<0或x>1.
16.4.
三、解答题
17.解:①列表:
②描点:把表中的对应的数值作为点的坐标在坐标系中描出来,
③连线:用平滑的线顺次连起来.
18.解:∵反比例函数y=(3m﹣1)的图象在第二、四象限,
∴m2﹣2=﹣1,3m﹣1<0,
∴m=﹣1.
19.解:∵y1与x2成正比例,y2与x成反比例,
∴y1=kx2,y2=,
∵y=y1+y2,
∴y=kx2+,
∵当x=时y=5,当x=1时y=﹣1,
∴,
解得:,
∴y与x之间的函数关系式为y=﹣4x2+.
20.解:(1)将点A(m,2)代入y=2x﹣4得:
2m﹣4=2,
解得:m=3,
∴点A的坐标为(3,2);
(2)将点A(3,2)代入y=得:k=6,
∴反比例函数解析式为y=.
21.解:(1)把A(2,3)代入y=得k=2×3=6,
所以反比例函数解析式为y=;
(2)当x=﹣4时,y==﹣=﹣.
22.解:(1)∵矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm),
∴xy=6,
故y与x之间的函数关系式为:y=,自变量的取值范围是:x>0;
(2)如图所示:
.
23.解:(1)当y=2时,则x==4.即点A的坐标是(4,2);
(2)S△BOB'=×8=4;
(3)在y=中,当x=2时,y==4,则B的坐标是(2,4),
根据反比例函数的解析式,知三角形OAA1的面积和三角形OBB1的面积相等,都是4,
则直角梯形ABB1A1的面积是×(2+4)×2=6.
24.解:(1)设反比例函数图象的解析式为y=,
由图得,反比例函数上一点坐标为(0.04,3200)代入y=,有k=0.04×3200=128,
又题中实际意义需x>0.
∴y=(x>0).
(2)①∵可装汽油500L,若汽车每小时用油量为xL,
∴用油时间yh与每小时的用油量xL之间的函数表达式可表示为y=;
②每小时的用油量为25L,则这些油可用的时间为500÷25=20小时;
③如果要使汽车连续行驶50h不需加油,那么每小时用油量的取值范围0≤x<10;
故答案为:y=(x>0).y=;20;0≤x<10;
25.解:(1)设函数关系式为,
∵函数图象经过(10,2)
∴
∴k=20,
∴
∵0<x<16,0<y<8,
∴0<x<16,0<<8,
∴<x<16;
(2)∵
∴xy=20,
∴SE=S正=162﹣2×20=216;
(3)当x=6时,,
当x=12时,,
∴小矩形的长是6≤x≤12cm,小矩形宽的范围为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
