六年级数学上册第五单元《 圆 》说课课件(共29张PPT)
文档属性
| 名称 | 六年级数学上册第五单元《 圆 》说课课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 06:06:54 | ||
图片预览







文档简介
(共29张PPT)
学校:X小学
说课人:X
把握整体意义关联 促进思维结构发展
人教版(2022) 六年级数学上册 第五单元 《 圆 》
单元主题解读
单元目标拟定
关键内容确定
单元整合框架及说明
01
03
02
04
05
关键活动设计
01
单元主题解读
(从课程标准、单元教材内容、学生认知情况方面解读)
课程标准
全面普及义务教育,教育需求从“有学上”, 转向“上好学”,明确“培养什么人、怎样培养人、为谁培养人”。
数学课程目标要以学生发展为本,以核心素养为导向,进一步使学生获得数学基础知识、基本技能、基本思想和基本活动经验的获得与发展,发展运用数学知识与方法发现、提出、分析和解决问题的能力,形成正确的情感、态度和价值观。
数学课程要培养学生的核心素养,会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界。
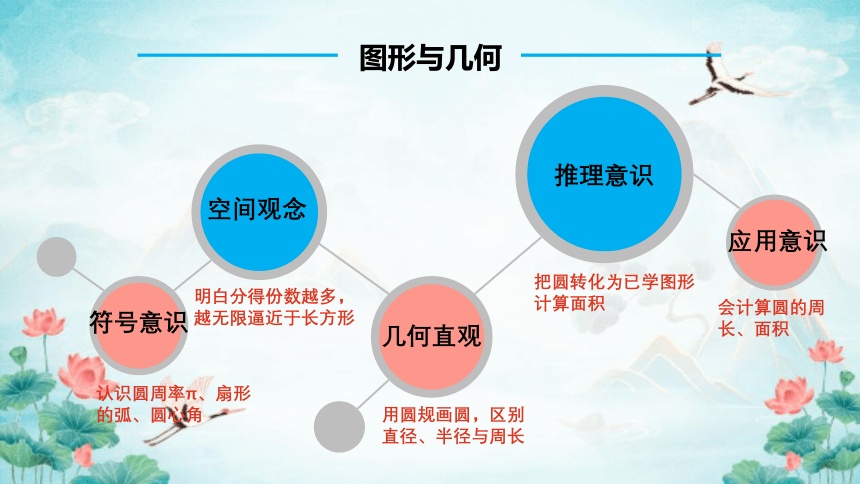
核心素养具体表现为:数感、量感、符号意识、运算能力、几何直观、空间观念、推理意识、数据意识、模型意识、应用意识、创新意识。
图形与几何
用圆规画圆,区别直径、半径与周长
明白分得份数越多,越无限逼近于长方形
认识圆周率π、扇形的弧、圆心角
把圆转化为已学图形计算面积
会计算圆的周长、面积
符号意识
空间观念
几何直观
推理意识
应用意识
圆的认识
圆的周长
圆的面积
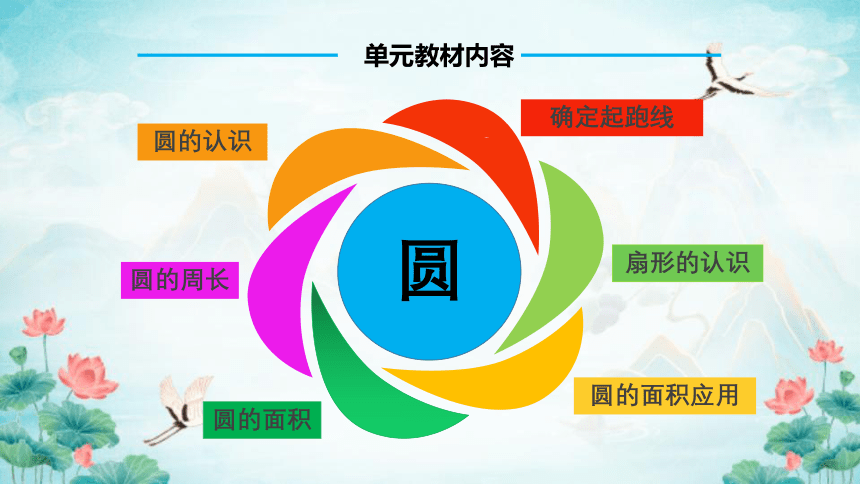
确定起跑线
扇形的认识
圆的面积应用
单元教材内容
圆
圆的认识
圆的周长
教材利用学生已有经验,创设生活情境,借助生活中的圆,联系生活实际,用多种方法画圆,用圆规画圆的方法认识圆心、半径、直径以及半径、直径的关系等,通过用多个不同大小的圆片,经过折一折、画一画、量一量等方法,知道圆心确定圆的位置,半径决定圆的大小,在同圆(等圆)中,有无数条半径、直径,并每条半径、直径都相等。
教材从解决问题实际问题引入,突出探究圆的周长的必要性,利用滚圆法、绳绕法,引导学生在测量活动中探究圆的周长与直径之间的关系,理解圆周率的概念和圆的周长计算公式,通过动手操作、实际验证等活动,在变化中发现不变,发展学生的猜想、归纳能力,培养学生解决生活实际问题的能力。
圆的面积
圆的面积应用
从解决实际问题出发,引导学生用转化的方法把圆转化为长方形来计算面积,通过这一过程,让学生深刻体会到“化曲为直”“无限逼近”“一一对应”和“等积变换”的数学思想。
教材安排了解决生活中的圆的面积计算,圆环面积的计算以及“外方内圆”“外圆内方”两种特殊图形的面积计算。为学生提供了探索问题解决方法的机会,使学生进一步提高解决问题的能力。
扇形的认识
确定起跑线
紧贴学生已有知识,借助生活中的图片“扇贝”“扇形藻”“折扇”创设情境,激发学生的学习兴趣,直观认识扇形,掌握扇形的特征,理解圆心角,感受到扇形的大小与圆心角的大小有关,理解圆心角是180°和90°的扇形的特征。
教材安排了综合实践课,综合培养学生解决问题的能力,借助生活中的椭圆式圆形跑道,确定起跑线的起跑位置,通过动手操作、合作探究,量一量、算一算等方法,算出每条跑道之间相差的距离。
学生认知情况
基础知识
基本技能
基本思想
基本活动经验
认识了长方形、正方形、三角形、平行四边形、梯形,并会计算它们的周长、面积
初步掌握了图形的分割、拼移、转化等方法
初次认识、使用圆规,对圆的半径、直径、面积计算以及扇形的弧、圆心角是陌生的
02
单元目标拟定
单元目标拟定
基础知识
认识圆,会用圆规画圆,掌握圆的基本特征;认识扇形,掌握扇形的基本特征。
基本技能
会利用直尺和圆规,设计与圆有关的图案;通过实践操作,理解圆周率的意义,理解和掌握圆的周长、面积计算公式,并解决生活中相应的实际问题。
基本思想
在推导圆的周长与面积的计算过程中体会和掌握转化、极限等数学思想。
基本活动经验
经历尝试、探究、分析、反思等过程,培养数学活动经验,解决与圆有关的数学问题过程中,提高解决问题的能力;通过生活实例、数学史料,感受数学之美,了解数学文化,提高学习兴趣。
03
关键内容确定
周长
圆
面积
圆的认识
扇形
定义
相关概念
性质
在同一平面内到定点的距离等于定长的点的集合叫做圆
针尖所在的点叫做圆心
连接圆心和圆上任意一点的线段叫做半径
通过圆心并且两端都在圆上的线段叫做直径
圆心确定圆的位置,半径确定圆的大小
半径相等的圆叫做等圆,等圆通过平移可以完全重合
圆心重合,半径不等的两个圆叫做同心圆
在同一个圆内,所有半径相等,所有直径相等
在同一个圆内,有无数条半径,有无数条直径
在同一个圆内,直径的长度是半径的2倍
定义
圆周率
周长公式
变化规律
半圆周长
围成圆的曲线的长度叫做圆的周长
圆的周长和直径的比值,用字母π表示
圆周率是个无限不循环小数,π≈3.14
C=πd=2πr
半径扩大几倍,直径、周长也扩大几倍;圆周长扩大的倍数与半径、直径扩大的倍数相同
C=πr+d
定义
面积公式
变化规律
环形面积
圆所占平面的大小叫做圆的面积
S=πr2
半径扩大几倍,直径、周长也扩大几倍,圆面积扩大的倍数是半径、直径扩大的倍数的平方倍
大圆面积-小圆面积=πR2-πr2=π(R2-r2)
定义
圆心角
面积
圆上任意两点之间的部分叫做弧,一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形
顶点所在圆心的角叫做圆心角
在同一平面内,扇形的大小与圆心角的大小无关
S=πr2×n/360
特殊情况
90°
180°
S=1/4πr2
S=1/2πr2
04
单元整合框架及说明
单元整合框架及说明
这一单元安排了“圆的认识”、“圆的周长”“圆的面积”、“扇形的认识”及综合实践活动“确定起跑线”,这四个内容由易到难,层层深入。
学生已认识长方形、正方形、三角形等平面图形,并会计算它们的周长和面积,圆是最后一个平面图形。从教材的编排体系可以看出,圆是一种曲线图形,而前面学习的是直线图形,圆的教学是学生认识曲线图形的开始。通过对圆的研究,渗透了曲线图形与直线图形的内在联系,体现了“化圆为方”、“化曲为直”的转化思想,“无限逼近”的极限思想,以及“等积变形”“对应”“转化”的数学思想。让学生掌握圆的一些基础知识,感悟数学思想方法,加强学生的动手操作能力,培养学生良好的数学核心素养。
05
关键活动设计
关键活动设计
TITLE HERE
圆的认识
为了让学生掌握圆的特征,认识圆的各部分名称,理解同圆或等圆里半径与直径的关系,每人一份学具袋,有大小不一的圆,我设计了量一量、比一比、画一画等动手操作活动。
点击输入简要文字介绍,文字内容需,言简意赅的说明分项内容……。
Year 2016
Year 20XX
观察对比,确定圆心,区分半径与直径
r
O
O
r
r
O
圆的大小不同。
连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。半径的长度就是圆规两脚间的距离,半径确定圆的大小。
用学具袋的圆,仔细观察,画一画、量一量,这些线段有什么特点?能画几条这样的线段?
一个圆内,有无数条半径,每条半径都相等。
用圆规画圆时,针尖所在的点叫做圆心,一般用字母O表示。
圆的位置不同。
圆心确定圆的位置。
r
O
d
d
O
r
r
d
O
通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示。
一个圆中也有无数条直径,每条直径都相等。
在同一个圆中,直径的长度是半径的2倍。
d=2r 或r= d
用准备的三个圆量一量,画一画,观察比较,直径与半径的关系
12cm
6cm
2cm
4cm
8cm
4cm
关键活动设计
TITLE HERE
圆的周长
学生已认识圆的周长,本课重点是研究圆的周长与直径的关系,学生通过测量、计算,能发现圆的周长与直径的倍数关系,根据这一倍数关系理解圆周率的意义,推导出圆周长的计算公式,培养学生的观察、比较、分析、综合及动手操作能力。我设计了大胆猜想、设法验证、分析数据、得出结论。
红色线是圆的直径,黑色线是圆的周长,请认真观察并比较,有什么发现?
基于观察,大胆猜想
①直径越长,周长就越长,直径越短,周长就越短。②周长和直径存在倍数关系。③周长与直径的商不变。
设法验证,理解数据
圆的周长与直径的商到底是不是一个确定不变的数,还得进一步验证。拿出课前准备的圆片、硬币、易拉罐,利用滚动法、绳测法测量手中圆的周长,量出直径,观察周长与直径的关系。
圆的周长(cm) 圆的直径(cm) 周长÷直径(保留两位小数)
25 8 3.13
19 6 3.17
20 6 3.33
24.9 8 3.11
18.9 6 3.15
19.1 6 3.18
25.1 8 3.14
周长都是直径的3倍多一些
圆周率通常保留两位小数,是一个无限不循环小数,取近似值3.14,C÷d=π
对比反思,反复验证
关键活动设计
TITLE HERE
圆的面积
学生已学过三角形、长方形、正方形、平行四边形、梯形等图形的面积计算,知道利用剪、拼、移的方法,研究图形之间的关系,从而推导公式,并渗透“转化”“极限”的数学思想。圆是曲线图形,要处理好曲线平面图形与直线平面图形关系,把曲线平面图形转化为直线平面图形,推导圆的面积计算公式。我设计了复习旧知,回忆转化,实践操作,探究公式四个关键设计。
复习旧知,回忆转化
将新图形转化成已学过的图形来推导面积的计算公式。
利用转化的方法,把圆转化成学过的长方形、平行四边形、三角形或梯形来研究。
输入标题
圆
近似的长方形
圆的半径 = 长方形的宽
割补转化
面积相等
长(a)
半径
r
宽(b)
宽(b)
圆周长的一半 = 长方形的长
长方形的面积 = 长 × 宽
圆的面积 = 圆周长的一半 × 半径
长(a)
S = πr × r = πr2
实践操作,探究公式
C÷2=πr
关键活动设计
TITLE HERE
扇形的认识
理解和建立扇形概念,认识圆心角和弧,在认识圆心角和弧的过程中,培养学生的观察能力。因此,我设计了创设情境,欣赏扇子,观察辨析,认识特征两个关键设计。
扇形中有两条线段,它们都是圆的半径。
都有一条曲线,这条曲线在圆上。
r
r
r
r
r
r
创设情境,欣赏扇子
输入标题
你能发现它们有哪些共同的特点?
像这样圆上两点(A、B)之间的部分叫做弧。
r
r
A
B
读作:弧AB
O
∠AOB是圆心角
这样顶点在圆心的角叫做圆心角。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
观察辨析,认识特征
说课人:X
日期:2022.10.25
谢谢您的观看!
学校:X小学
说课人:X
把握整体意义关联 促进思维结构发展
人教版(2022) 六年级数学上册 第五单元 《 圆 》
单元主题解读
单元目标拟定
关键内容确定
单元整合框架及说明
01
03
02
04
05
关键活动设计
01
单元主题解读
(从课程标准、单元教材内容、学生认知情况方面解读)
课程标准
全面普及义务教育,教育需求从“有学上”, 转向“上好学”,明确“培养什么人、怎样培养人、为谁培养人”。
数学课程目标要以学生发展为本,以核心素养为导向,进一步使学生获得数学基础知识、基本技能、基本思想和基本活动经验的获得与发展,发展运用数学知识与方法发现、提出、分析和解决问题的能力,形成正确的情感、态度和价值观。
数学课程要培养学生的核心素养,会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界。
核心素养具体表现为:数感、量感、符号意识、运算能力、几何直观、空间观念、推理意识、数据意识、模型意识、应用意识、创新意识。
图形与几何
用圆规画圆,区别直径、半径与周长
明白分得份数越多,越无限逼近于长方形
认识圆周率π、扇形的弧、圆心角
把圆转化为已学图形计算面积
会计算圆的周长、面积
符号意识
空间观念
几何直观
推理意识
应用意识
圆的认识
圆的周长
圆的面积
确定起跑线
扇形的认识
圆的面积应用
单元教材内容
圆
圆的认识
圆的周长
教材利用学生已有经验,创设生活情境,借助生活中的圆,联系生活实际,用多种方法画圆,用圆规画圆的方法认识圆心、半径、直径以及半径、直径的关系等,通过用多个不同大小的圆片,经过折一折、画一画、量一量等方法,知道圆心确定圆的位置,半径决定圆的大小,在同圆(等圆)中,有无数条半径、直径,并每条半径、直径都相等。
教材从解决问题实际问题引入,突出探究圆的周长的必要性,利用滚圆法、绳绕法,引导学生在测量活动中探究圆的周长与直径之间的关系,理解圆周率的概念和圆的周长计算公式,通过动手操作、实际验证等活动,在变化中发现不变,发展学生的猜想、归纳能力,培养学生解决生活实际问题的能力。
圆的面积
圆的面积应用
从解决实际问题出发,引导学生用转化的方法把圆转化为长方形来计算面积,通过这一过程,让学生深刻体会到“化曲为直”“无限逼近”“一一对应”和“等积变换”的数学思想。
教材安排了解决生活中的圆的面积计算,圆环面积的计算以及“外方内圆”“外圆内方”两种特殊图形的面积计算。为学生提供了探索问题解决方法的机会,使学生进一步提高解决问题的能力。
扇形的认识
确定起跑线
紧贴学生已有知识,借助生活中的图片“扇贝”“扇形藻”“折扇”创设情境,激发学生的学习兴趣,直观认识扇形,掌握扇形的特征,理解圆心角,感受到扇形的大小与圆心角的大小有关,理解圆心角是180°和90°的扇形的特征。
教材安排了综合实践课,综合培养学生解决问题的能力,借助生活中的椭圆式圆形跑道,确定起跑线的起跑位置,通过动手操作、合作探究,量一量、算一算等方法,算出每条跑道之间相差的距离。
学生认知情况
基础知识
基本技能
基本思想
基本活动经验
认识了长方形、正方形、三角形、平行四边形、梯形,并会计算它们的周长、面积
初步掌握了图形的分割、拼移、转化等方法
初次认识、使用圆规,对圆的半径、直径、面积计算以及扇形的弧、圆心角是陌生的
02
单元目标拟定
单元目标拟定
基础知识
认识圆,会用圆规画圆,掌握圆的基本特征;认识扇形,掌握扇形的基本特征。
基本技能
会利用直尺和圆规,设计与圆有关的图案;通过实践操作,理解圆周率的意义,理解和掌握圆的周长、面积计算公式,并解决生活中相应的实际问题。
基本思想
在推导圆的周长与面积的计算过程中体会和掌握转化、极限等数学思想。
基本活动经验
经历尝试、探究、分析、反思等过程,培养数学活动经验,解决与圆有关的数学问题过程中,提高解决问题的能力;通过生活实例、数学史料,感受数学之美,了解数学文化,提高学习兴趣。
03
关键内容确定
周长
圆
面积
圆的认识
扇形
定义
相关概念
性质
在同一平面内到定点的距离等于定长的点的集合叫做圆
针尖所在的点叫做圆心
连接圆心和圆上任意一点的线段叫做半径
通过圆心并且两端都在圆上的线段叫做直径
圆心确定圆的位置,半径确定圆的大小
半径相等的圆叫做等圆,等圆通过平移可以完全重合
圆心重合,半径不等的两个圆叫做同心圆
在同一个圆内,所有半径相等,所有直径相等
在同一个圆内,有无数条半径,有无数条直径
在同一个圆内,直径的长度是半径的2倍
定义
圆周率
周长公式
变化规律
半圆周长
围成圆的曲线的长度叫做圆的周长
圆的周长和直径的比值,用字母π表示
圆周率是个无限不循环小数,π≈3.14
C=πd=2πr
半径扩大几倍,直径、周长也扩大几倍;圆周长扩大的倍数与半径、直径扩大的倍数相同
C=πr+d
定义
面积公式
变化规律
环形面积
圆所占平面的大小叫做圆的面积
S=πr2
半径扩大几倍,直径、周长也扩大几倍,圆面积扩大的倍数是半径、直径扩大的倍数的平方倍
大圆面积-小圆面积=πR2-πr2=π(R2-r2)
定义
圆心角
面积
圆上任意两点之间的部分叫做弧,一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形
顶点所在圆心的角叫做圆心角
在同一平面内,扇形的大小与圆心角的大小无关
S=πr2×n/360
特殊情况
90°
180°
S=1/4πr2
S=1/2πr2
04
单元整合框架及说明
单元整合框架及说明
这一单元安排了“圆的认识”、“圆的周长”“圆的面积”、“扇形的认识”及综合实践活动“确定起跑线”,这四个内容由易到难,层层深入。
学生已认识长方形、正方形、三角形等平面图形,并会计算它们的周长和面积,圆是最后一个平面图形。从教材的编排体系可以看出,圆是一种曲线图形,而前面学习的是直线图形,圆的教学是学生认识曲线图形的开始。通过对圆的研究,渗透了曲线图形与直线图形的内在联系,体现了“化圆为方”、“化曲为直”的转化思想,“无限逼近”的极限思想,以及“等积变形”“对应”“转化”的数学思想。让学生掌握圆的一些基础知识,感悟数学思想方法,加强学生的动手操作能力,培养学生良好的数学核心素养。
05
关键活动设计
关键活动设计
TITLE HERE
圆的认识
为了让学生掌握圆的特征,认识圆的各部分名称,理解同圆或等圆里半径与直径的关系,每人一份学具袋,有大小不一的圆,我设计了量一量、比一比、画一画等动手操作活动。
点击输入简要文字介绍,文字内容需,言简意赅的说明分项内容……。
Year 2016
Year 20XX
观察对比,确定圆心,区分半径与直径
r
O
O
r
r
O
圆的大小不同。
连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。半径的长度就是圆规两脚间的距离,半径确定圆的大小。
用学具袋的圆,仔细观察,画一画、量一量,这些线段有什么特点?能画几条这样的线段?
一个圆内,有无数条半径,每条半径都相等。
用圆规画圆时,针尖所在的点叫做圆心,一般用字母O表示。
圆的位置不同。
圆心确定圆的位置。
r
O
d
d
O
r
r
d
O
通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示。
一个圆中也有无数条直径,每条直径都相等。
在同一个圆中,直径的长度是半径的2倍。
d=2r 或r= d
用准备的三个圆量一量,画一画,观察比较,直径与半径的关系
12cm
6cm
2cm
4cm
8cm
4cm
关键活动设计
TITLE HERE
圆的周长
学生已认识圆的周长,本课重点是研究圆的周长与直径的关系,学生通过测量、计算,能发现圆的周长与直径的倍数关系,根据这一倍数关系理解圆周率的意义,推导出圆周长的计算公式,培养学生的观察、比较、分析、综合及动手操作能力。我设计了大胆猜想、设法验证、分析数据、得出结论。
红色线是圆的直径,黑色线是圆的周长,请认真观察并比较,有什么发现?
基于观察,大胆猜想
①直径越长,周长就越长,直径越短,周长就越短。②周长和直径存在倍数关系。③周长与直径的商不变。
设法验证,理解数据
圆的周长与直径的商到底是不是一个确定不变的数,还得进一步验证。拿出课前准备的圆片、硬币、易拉罐,利用滚动法、绳测法测量手中圆的周长,量出直径,观察周长与直径的关系。
圆的周长(cm) 圆的直径(cm) 周长÷直径(保留两位小数)
25 8 3.13
19 6 3.17
20 6 3.33
24.9 8 3.11
18.9 6 3.15
19.1 6 3.18
25.1 8 3.14
周长都是直径的3倍多一些
圆周率通常保留两位小数,是一个无限不循环小数,取近似值3.14,C÷d=π
对比反思,反复验证
关键活动设计
TITLE HERE
圆的面积
学生已学过三角形、长方形、正方形、平行四边形、梯形等图形的面积计算,知道利用剪、拼、移的方法,研究图形之间的关系,从而推导公式,并渗透“转化”“极限”的数学思想。圆是曲线图形,要处理好曲线平面图形与直线平面图形关系,把曲线平面图形转化为直线平面图形,推导圆的面积计算公式。我设计了复习旧知,回忆转化,实践操作,探究公式四个关键设计。
复习旧知,回忆转化
将新图形转化成已学过的图形来推导面积的计算公式。
利用转化的方法,把圆转化成学过的长方形、平行四边形、三角形或梯形来研究。
输入标题
圆
近似的长方形
圆的半径 = 长方形的宽
割补转化
面积相等
长(a)
半径
r
宽(b)
宽(b)
圆周长的一半 = 长方形的长
长方形的面积 = 长 × 宽
圆的面积 = 圆周长的一半 × 半径
长(a)
S = πr × r = πr2
实践操作,探究公式
C÷2=πr
关键活动设计
TITLE HERE
扇形的认识
理解和建立扇形概念,认识圆心角和弧,在认识圆心角和弧的过程中,培养学生的观察能力。因此,我设计了创设情境,欣赏扇子,观察辨析,认识特征两个关键设计。
扇形中有两条线段,它们都是圆的半径。
都有一条曲线,这条曲线在圆上。
r
r
r
r
r
r
创设情境,欣赏扇子
输入标题
你能发现它们有哪些共同的特点?
像这样圆上两点(A、B)之间的部分叫做弧。
r
r
A
B
读作:弧AB
O
∠AOB是圆心角
这样顶点在圆心的角叫做圆心角。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
观察辨析,认识特征
说课人:X
日期:2022.10.25
谢谢您的观看!
