九年级数学下册试题 1.1-1.2 锐角三角函数及其特殊值-北师大版(含答案)
文档属性
| 名称 | 九年级数学下册试题 1.1-1.2 锐角三角函数及其特殊值-北师大版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 873.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 15:46:27 | ||
图片预览




文档简介
1.1-1.2 锐角三角函数及其特殊值
第一课时
一、单选题
1.在中,,的余弦是( )
A. B. C. D.
2.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
3.在中,,,,则的值为( )
A. B. C. D.
4.已知在Rt△ABC中,∠C=90°,若sinA=,则cosA等于( )
A. B. C. D.1
5.的值等于( )
A. B. C.1 D.
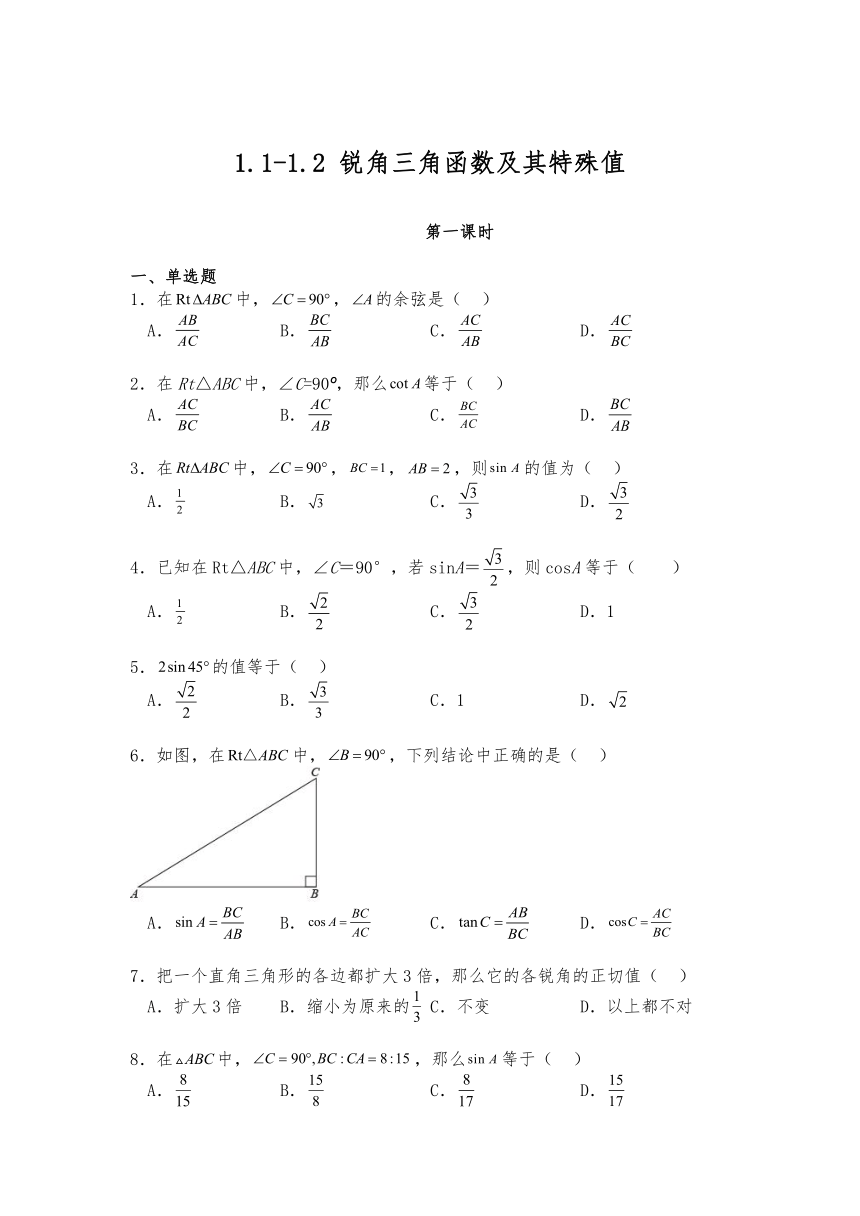
6.如图,在中,,下列结论中正确的是( )
A. B. C. D.
7.把一个直角三角形的各边都扩大3倍,那么它的各锐角的正切值( )
A.扩大3倍 B.缩小为原来的 C.不变 D.以上都不对
8.在中,,那么等于( )
A. B. C. D.
9.在中,,则的值是( ).
A. B. C. D.
10.中,的值是( ).
A. B. C. D.
11.已知∠A,∠B均为锐角,且cosA=,sinB=,则下列结论中正确的是( )
A.∠A=∠B=60° B.∠A=∠B=30°
C.∠A=30°,∠B=60° D.∠A=60°,∠B=30°
12.点关于x轴的对称点的坐标是( )
A. B. C. D.
二、填空题
13.cos45°-tan60°=________;
14.如图,各三角形的顶点都在方格纸的格点上,则_______,_______,_______.
15.已知α是锐角,,则α等于 _________.
16.在中,,则的形状是__________.
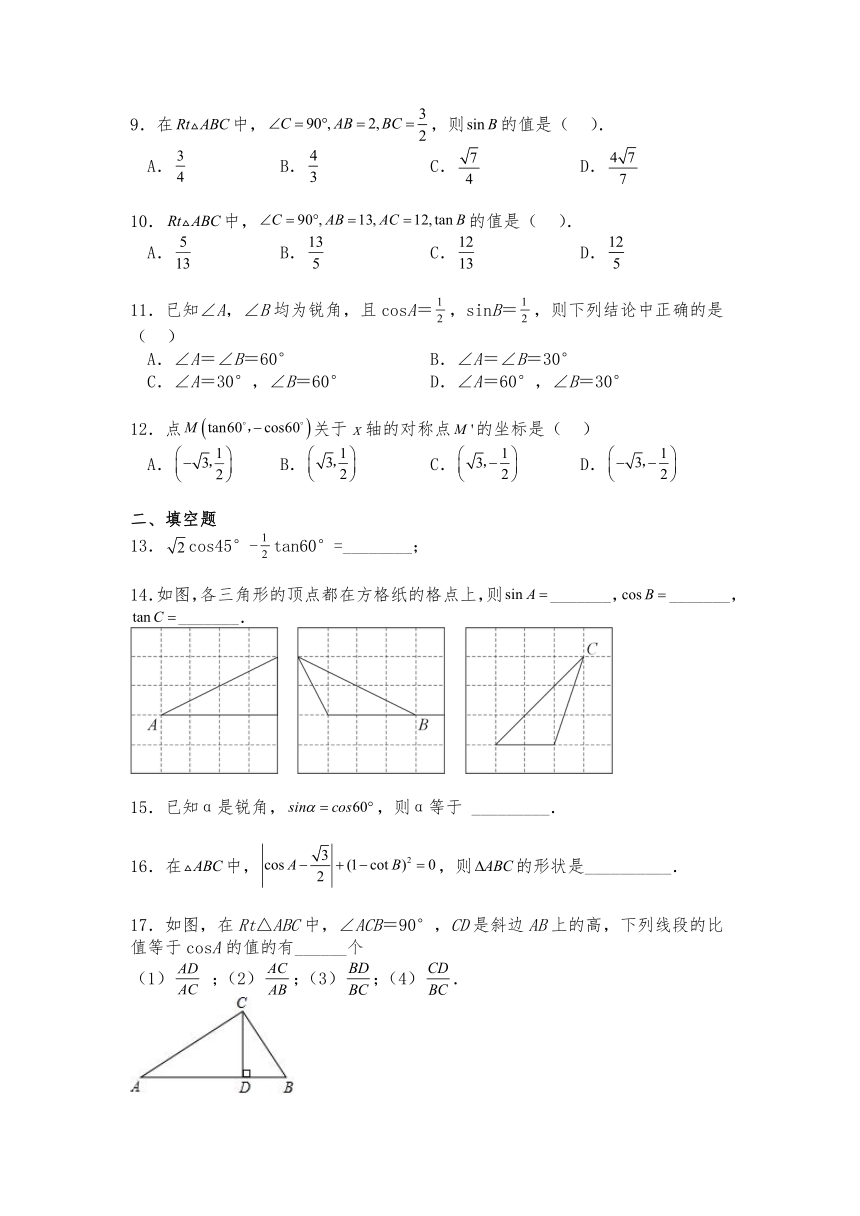
17.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,下列线段的比值等于cosA的值的有______个
(1) ;(2);(3);(4).
18.如图,、分别是中、边上的高,,则________.
19.在中,.
20.已知,且为锐角,则的取值范围是__________.
三、解答题
21.分别求出图中,的正弦值、余弦值和正切值.
22.如图,定义:在中,锐角的邻边与对边的比叫做的余切,记作,即.根据上述角的余切定义,解下列问题:
(1)________;
(2)如上图,已知,其中为锐角,则的值为_______.
23.计算:
(1); (2);
(3).
第二课时
一、单选题
1.在直角三角形ABC中,,则的值是( )
A. B. C. D.3
2.在Rt中,∠C=90°,∠B=60°,那么sinA+cosB的值为( )
A.1 B. C. D.
3.如果,那么=( ).
A.30° B.45° C.60° D.90°
4.如图,在△ABC中,∠ABC=45°,点H是高AD和BE的交点,∠CAD=30°,CD=4,则线段BH的长度为( )
A.6 B. C.8 D.
5.如图,正方形的边长为6,为对角线,取中点E,与交于点F则等于( )
A. B. C. D.
6.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=,tan∠BA3C=…,依此规律写出tan∠BA7C=,则n=( )
A.40 B.41 C.42 D.43
7.如图,中,,,的值为,则( )
A. B. C. D.
二、填空题
8.在直角三角形ABC中,若cosC=,则=________.
9.一个直角三角形的两边长分别为3和4,则较小的锐角的正切值是___________.
10.△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C=_____.
11.如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为 _____.
12.如图,在四边形中,,平分.若,,则______.
三、解答题
13.计算或化简:
(1)cos30°+sin45°; (2)·tan 30°;
(3)(sin60°+cos 45°)(sin 60°-cos 45°);
(4)6tan2 30°-sin 60°-2sin 45°.
14.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
15.如图,AD是△ABC的中线, .求:
(1)BC的长;
(2)∠ADC的正弦值.
16.如图,在的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹.
(1)在图①中画一条射线,使.
(2)在图②中画一条射线,使.
17.如图,在中,是对角线、的交点,,,垂足分别为点、.
(1)求证:.
(2)若,,求的值.
18.阅读下面的材料,先完成阅读填空,再按要求答题.
sin230°+cos230°=____;
sin245°+cos245°=____;
sin260°+cos260°=____;
……
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=____.
19.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
20.如图,已知∠ABC和射线BD上一点P(点P与点B不重合,且点P到BA,BC的距离分别为PE,PF).
(1)若∠EBP=40°,∠FBP=20°,试比较PE,PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β,请判断PE,PF的大小,并给出证明.
第一课时答案
一、单选题
C.A.A.A.D.C.C.C.C.D.D.B.
二、填空题
13..
14.
15.30°.
16.钝角三角形
17.3.
18..
19.6.
20.
三、解答题
21.解:图(1)由勾股定理得:
∴,,,,,;
图(2)由勾股定理得:
,,, ,,;
图(3)由勾股定理得:
,,, ,,;
22.(1)如图,
∵中,,
∴,
∴,
∴;
故答案为:.
(2)∵,
∴设,
∴.
故答案为:
23.(1);
(2)
(3)
第二课时答案
一、单选题
A.A.A.C.B.D.D.
二、填空题
8.或
9.或.
10.60°.
11..
12..
三、解答题
13.(1)原式==+1=;
(2)原式===;
(3)原式=sin260°-cos245°=()2-()2=-=;
(4)原式=6×()2--2×=2-=-.
14.(1)∵点B(4,2),BA⊥x轴于A,
∴OA=4,AB=2,
tan∠BOA===;
(2)如图,由旋转可知:CD=BA=2,OD=OA=4,
∴点C的坐标是(﹣2,4).
15.解:(1)如图,过点A作于点H,
在中,
∵,,
∴,
∴
在中,
∵,
∴,
∴;
(2)∵,
∴,,
∴,
在中,,
∴的正弦值是.
16.解:(1)如图所示.
(2)如图所示.
17.解:(1)证明:在中,
∵,
∴
∴
又∵
∴
∴
(2)∵,
∴
∵
∴
在中,,.
18.sin230°+cos230°==1 ,
sin245°+cos245°==1 ,
sin260°+cos260°==1 ,
即可猜想出:对任意锐角,都有
故答案为:1;1;1;1
19.∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==,
在Rt△ABC中,cosB=.
20.
(1)∵ PE⊥AB,PF⊥BC,∴ sin ∠EBP==sin 40°,sin ∠FBP==sin 20°.
又∵sin 40°>sin 20°,∴>,∴PE>PF.
(2)∵α,β都是锐角,且α>β,∴sin α>sin β.
又∵sin ∠EBP==sin α,sin ∠FBP==sin β,
∴>,∴PE>PF.
第一课时
一、单选题
1.在中,,的余弦是( )
A. B. C. D.
2.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
3.在中,,,,则的值为( )
A. B. C. D.
4.已知在Rt△ABC中,∠C=90°,若sinA=,则cosA等于( )
A. B. C. D.1
5.的值等于( )
A. B. C.1 D.
6.如图,在中,,下列结论中正确的是( )
A. B. C. D.
7.把一个直角三角形的各边都扩大3倍,那么它的各锐角的正切值( )
A.扩大3倍 B.缩小为原来的 C.不变 D.以上都不对
8.在中,,那么等于( )
A. B. C. D.
9.在中,,则的值是( ).
A. B. C. D.
10.中,的值是( ).
A. B. C. D.
11.已知∠A,∠B均为锐角,且cosA=,sinB=,则下列结论中正确的是( )
A.∠A=∠B=60° B.∠A=∠B=30°
C.∠A=30°,∠B=60° D.∠A=60°,∠B=30°
12.点关于x轴的对称点的坐标是( )
A. B. C. D.
二、填空题
13.cos45°-tan60°=________;
14.如图,各三角形的顶点都在方格纸的格点上,则_______,_______,_______.
15.已知α是锐角,,则α等于 _________.
16.在中,,则的形状是__________.
17.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,下列线段的比值等于cosA的值的有______个
(1) ;(2);(3);(4).
18.如图,、分别是中、边上的高,,则________.
19.在中,.
20.已知,且为锐角,则的取值范围是__________.
三、解答题
21.分别求出图中,的正弦值、余弦值和正切值.
22.如图,定义:在中,锐角的邻边与对边的比叫做的余切,记作,即.根据上述角的余切定义,解下列问题:
(1)________;
(2)如上图,已知,其中为锐角,则的值为_______.
23.计算:
(1); (2);
(3).
第二课时
一、单选题
1.在直角三角形ABC中,,则的值是( )
A. B. C. D.3
2.在Rt中,∠C=90°,∠B=60°,那么sinA+cosB的值为( )
A.1 B. C. D.
3.如果,那么=( ).
A.30° B.45° C.60° D.90°
4.如图,在△ABC中,∠ABC=45°,点H是高AD和BE的交点,∠CAD=30°,CD=4,则线段BH的长度为( )
A.6 B. C.8 D.
5.如图,正方形的边长为6,为对角线,取中点E,与交于点F则等于( )
A. B. C. D.
6.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=,tan∠BA3C=…,依此规律写出tan∠BA7C=,则n=( )
A.40 B.41 C.42 D.43
7.如图,中,,,的值为,则( )
A. B. C. D.
二、填空题
8.在直角三角形ABC中,若cosC=,则=________.
9.一个直角三角形的两边长分别为3和4,则较小的锐角的正切值是___________.
10.△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C=_____.
11.如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为 _____.
12.如图,在四边形中,,平分.若,,则______.
三、解答题
13.计算或化简:
(1)cos30°+sin45°; (2)·tan 30°;
(3)(sin60°+cos 45°)(sin 60°-cos 45°);
(4)6tan2 30°-sin 60°-2sin 45°.
14.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
15.如图,AD是△ABC的中线, .求:
(1)BC的长;
(2)∠ADC的正弦值.
16.如图,在的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹.
(1)在图①中画一条射线,使.
(2)在图②中画一条射线,使.
17.如图,在中,是对角线、的交点,,,垂足分别为点、.
(1)求证:.
(2)若,,求的值.
18.阅读下面的材料,先完成阅读填空,再按要求答题.
sin230°+cos230°=____;
sin245°+cos245°=____;
sin260°+cos260°=____;
……
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=____.
19.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
20.如图,已知∠ABC和射线BD上一点P(点P与点B不重合,且点P到BA,BC的距离分别为PE,PF).
(1)若∠EBP=40°,∠FBP=20°,试比较PE,PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β,请判断PE,PF的大小,并给出证明.
第一课时答案
一、单选题
C.A.A.A.D.C.C.C.C.D.D.B.
二、填空题
13..
14.
15.30°.
16.钝角三角形
17.3.
18..
19.6.
20.
三、解答题
21.解:图(1)由勾股定理得:
∴,,,,,;
图(2)由勾股定理得:
,,, ,,;
图(3)由勾股定理得:
,,, ,,;
22.(1)如图,
∵中,,
∴,
∴,
∴;
故答案为:.
(2)∵,
∴设,
∴.
故答案为:
23.(1);
(2)
(3)
第二课时答案
一、单选题
A.A.A.C.B.D.D.
二、填空题
8.或
9.或.
10.60°.
11..
12..
三、解答题
13.(1)原式==+1=;
(2)原式===;
(3)原式=sin260°-cos245°=()2-()2=-=;
(4)原式=6×()2--2×=2-=-.
14.(1)∵点B(4,2),BA⊥x轴于A,
∴OA=4,AB=2,
tan∠BOA===;
(2)如图,由旋转可知:CD=BA=2,OD=OA=4,
∴点C的坐标是(﹣2,4).
15.解:(1)如图,过点A作于点H,
在中,
∵,,
∴,
∴
在中,
∵,
∴,
∴;
(2)∵,
∴,,
∴,
在中,,
∴的正弦值是.
16.解:(1)如图所示.
(2)如图所示.
17.解:(1)证明:在中,
∵,
∴
∴
又∵
∴
∴
(2)∵,
∴
∵
∴
在中,,.
18.sin230°+cos230°==1 ,
sin245°+cos245°==1 ,
sin260°+cos260°==1 ,
即可猜想出:对任意锐角,都有
故答案为:1;1;1;1
19.∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==,
在Rt△ABC中,cosB=.
20.
(1)∵ PE⊥AB,PF⊥BC,∴ sin ∠EBP==sin 40°,sin ∠FBP==sin 20°.
又∵sin 40°>sin 20°,∴>,∴PE>PF.
(2)∵α,β都是锐角,且α>β,∴sin α>sin β.
又∵sin ∠EBP==sin α,sin ∠FBP==sin β,
∴>,∴PE>PF.
