第三章 变量之间的关系 单元回顾与思考 教案(表格式) 北师大版数学七年级下册
文档属性
| 名称 | 第三章 变量之间的关系 单元回顾与思考 教案(表格式) 北师大版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 77.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 17:30:22 | ||
图片预览

文档简介
课题 章末总结 课型 新授课
教 学 目 标 1.总结表示变量之间关系的方法.
2.会用表示变量之间关系的各种形式分析变量之间的关系,
3.能用适当的方式表示实际情境中变量之间的关系,并进行简单的预测。
重点 能读懂表格、关系式、图象所表示的信息,.
难点 能用表格、关系式、图象刻画一些具体情境中变量之间的关系.
任务1:知识梳理 1、举例说明常量、变量; 2、 举例说明自变量和因变量; 3、表示变量之间关系的方法有哪些,各有什么特点。 任务2:典例学习 例1.一名同学在用弹簧做实验,在弹簧上挂不同质量的物体后,弹簧的长度就会发生变化,实验数据如下表: 所挂物体的质量/千克012345弹簧的长度/cm1212.51313.51414.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? (2)弹簧不挂物体时的长度是多少?如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势如何? (3)如果此时弹簧最大挂重量为15千克,你能预测当挂重为10千克时,弹簧的长度是多少? 例2.如图:将边长为20cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体。 (1)这个情境反映了哪两个变量之间的关系?其中自变量是什么?因变量是什么? (2)在以上问题中,若设截去的小正方形的边长是xcm,围成的无盖长方体的体积是ycm3,则y与x之间的关系式是__________________; (3)若小正方形的边长是5cm,那么长方体的体积是多少cm3?当x=2.5cm体积是多少cm3 (4)根据以上关系式填下表: x/cm123456789y/cm3
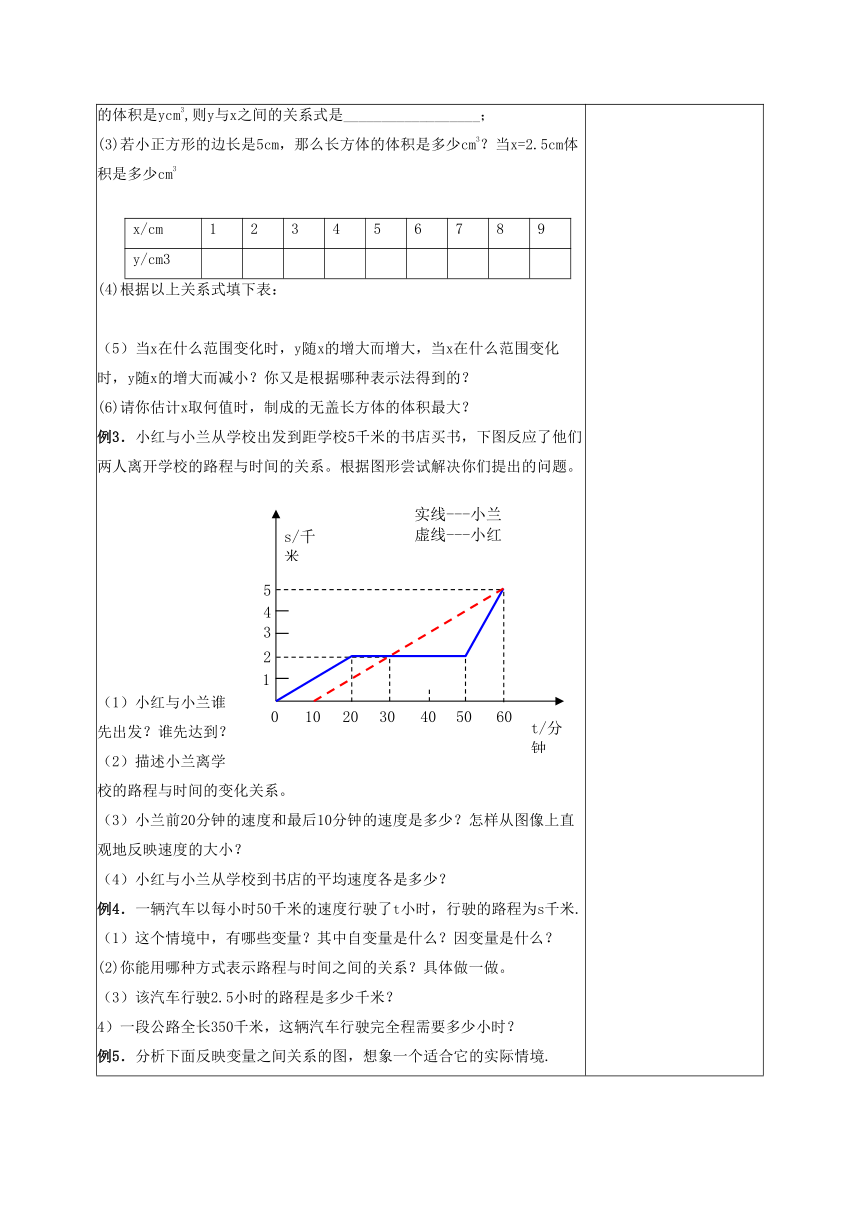
(5)当x在什么范围变化时,y随x的增大而增大,当x在什么范围变化时,y随x的增大而减小?你又是根据哪种表示法得到的? (6)请你估计x取何值时,制成的无盖长方体的体积最大? 例3.小红与小兰从学校出发到距学校5千米的书店买书,下图反应了他们两人离开学校的路程与时间的关系。根据图形尝试解决你们提出的问题。 (1)小红与小兰谁先出发?谁先达到? (2)描述小兰离学校的路程与时间的变化关系。 (3)小兰前20分钟的速度和最后10分钟的速度是多少?怎样从图像上直观地反映速度的大小? (4)小红与小兰从学校到书店的平均速度各是多少? 例4.一辆汽车以每小时50千米的速度行驶了t小时,行驶的路程为s千米. (1)这个情境中,有哪些变量?其中自变量是什么?因变量是什么? (2)你能用哪种方式表示路程与时间之间的关系?具体做一做。 (3)该汽车行驶2.5小时的路程是多少千米? 4)一段公路全长350千米,这辆汽车行驶完全程需要多少小时? 例5.分析下面反映变量之间关系的图,想象一个适合它的实际情境. 任务3:练习巩固 1. 2012年6月份某一天沈阳的气温随时间变化的情况如图所示,回答下列问题: (1)这天的最高气温约是 ℃; (2)这天一共有 个小时的气温在24℃以上; (3)这天在 范围内温度在上升; 这天在 范围内温度在下降; (4)请你预测一下,次日凌晨1点的气温大约多少度。 2.果子成熟从树上落到地面,它落下的高度与经过的时间有如下的关系: 时间t/秒0.50.60.70.80.91…高度 h/米5×0.255×0.365×0.495×0.645×0.815×1…
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? (2)如果果子经过2秒落到地上,那么请估计这果子开始落下时离地面的高度是多少米? (3)请你列出果子落下的高度h(米)与时间t(秒)之间的关系式。 3.某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t (1)请完成下表 汽车行驶时间t/小时012.54油箱的油量Q/升60
(2)汽车行驶5小时后,油箱中油量是 升 (3)若汽车行驶过程中,油箱的油量为12升,则汽车行驶了 小时 (4)贮满60升汽油的汽车,最多行驶 小时 (5)下面哪个图像能够反映变量Q与t的关系的是( ) 任务4:课堂小结 通过本节课的交流与学习,畅谈自己的收获的体会(本节课所学的知识,以及解决问题的过程中蕴含的数学思想与方法.) 任务5:作业 1:梳理第三单元知识点并整理成思维导图 2.完成单元复习题。
板 书 设 计
教 学 反 思
教 学 目 标 1.总结表示变量之间关系的方法.
2.会用表示变量之间关系的各种形式分析变量之间的关系,
3.能用适当的方式表示实际情境中变量之间的关系,并进行简单的预测。
重点 能读懂表格、关系式、图象所表示的信息,.
难点 能用表格、关系式、图象刻画一些具体情境中变量之间的关系.
任务1:知识梳理 1、举例说明常量、变量; 2、 举例说明自变量和因变量; 3、表示变量之间关系的方法有哪些,各有什么特点。 任务2:典例学习 例1.一名同学在用弹簧做实验,在弹簧上挂不同质量的物体后,弹簧的长度就会发生变化,实验数据如下表: 所挂物体的质量/千克012345弹簧的长度/cm1212.51313.51414.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? (2)弹簧不挂物体时的长度是多少?如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势如何? (3)如果此时弹簧最大挂重量为15千克,你能预测当挂重为10千克时,弹簧的长度是多少? 例2.如图:将边长为20cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体。 (1)这个情境反映了哪两个变量之间的关系?其中自变量是什么?因变量是什么? (2)在以上问题中,若设截去的小正方形的边长是xcm,围成的无盖长方体的体积是ycm3,则y与x之间的关系式是__________________; (3)若小正方形的边长是5cm,那么长方体的体积是多少cm3?当x=2.5cm体积是多少cm3 (4)根据以上关系式填下表: x/cm123456789y/cm3
(5)当x在什么范围变化时,y随x的增大而增大,当x在什么范围变化时,y随x的增大而减小?你又是根据哪种表示法得到的? (6)请你估计x取何值时,制成的无盖长方体的体积最大? 例3.小红与小兰从学校出发到距学校5千米的书店买书,下图反应了他们两人离开学校的路程与时间的关系。根据图形尝试解决你们提出的问题。 (1)小红与小兰谁先出发?谁先达到? (2)描述小兰离学校的路程与时间的变化关系。 (3)小兰前20分钟的速度和最后10分钟的速度是多少?怎样从图像上直观地反映速度的大小? (4)小红与小兰从学校到书店的平均速度各是多少? 例4.一辆汽车以每小时50千米的速度行驶了t小时,行驶的路程为s千米. (1)这个情境中,有哪些变量?其中自变量是什么?因变量是什么? (2)你能用哪种方式表示路程与时间之间的关系?具体做一做。 (3)该汽车行驶2.5小时的路程是多少千米? 4)一段公路全长350千米,这辆汽车行驶完全程需要多少小时? 例5.分析下面反映变量之间关系的图,想象一个适合它的实际情境. 任务3:练习巩固 1. 2012年6月份某一天沈阳的气温随时间变化的情况如图所示,回答下列问题: (1)这天的最高气温约是 ℃; (2)这天一共有 个小时的气温在24℃以上; (3)这天在 范围内温度在上升; 这天在 范围内温度在下降; (4)请你预测一下,次日凌晨1点的气温大约多少度。 2.果子成熟从树上落到地面,它落下的高度与经过的时间有如下的关系: 时间t/秒0.50.60.70.80.91…高度 h/米5×0.255×0.365×0.495×0.645×0.815×1…
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? (2)如果果子经过2秒落到地上,那么请估计这果子开始落下时离地面的高度是多少米? (3)请你列出果子落下的高度h(米)与时间t(秒)之间的关系式。 3.某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t (1)请完成下表 汽车行驶时间t/小时012.54油箱的油量Q/升60
(2)汽车行驶5小时后,油箱中油量是 升 (3)若汽车行驶过程中,油箱的油量为12升,则汽车行驶了 小时 (4)贮满60升汽油的汽车,最多行驶 小时 (5)下面哪个图像能够反映变量Q与t的关系的是( ) 任务4:课堂小结 通过本节课的交流与学习,畅谈自己的收获的体会(本节课所学的知识,以及解决问题的过程中蕴含的数学思想与方法.) 任务5:作业 1:梳理第三单元知识点并整理成思维导图 2.完成单元复习题。
板 书 设 计
教 学 反 思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
