19.2平行四边形 知识点分类练习题(含解析)沪科版八年级数学下册
文档属性
| 名称 | 19.2平行四边形 知识点分类练习题(含解析)沪科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 511.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 17:37:34 | ||
图片预览


文档简介
沪科版八年级数学下册《19.2平行四边形》知识点分类练习题(附答案)
一.平行四边形的性质
1.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积为( )
A.1.5 B. C. D.
2.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是( )
A.(3,1) B.(3,2) C.(3,3) D.(3,4)
3.如图,点O是 ABCD对角线的交点,EF过点O分别交AD,BC于点E,F.下列结论:①OE=OF;②AE=BF;③∠DOC=∠OCD;④∠CFE=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
4.在 ABCD中,若∠B=60°,AB=16,AC=14,则 ABCD的周长是 .
5.如图,在平行四边形ABCD中,AB=8,AD=6,以AB为边向右作等边△ABE,F为边CD上一点,DF=2,连接EF,则EF的最小值为 .
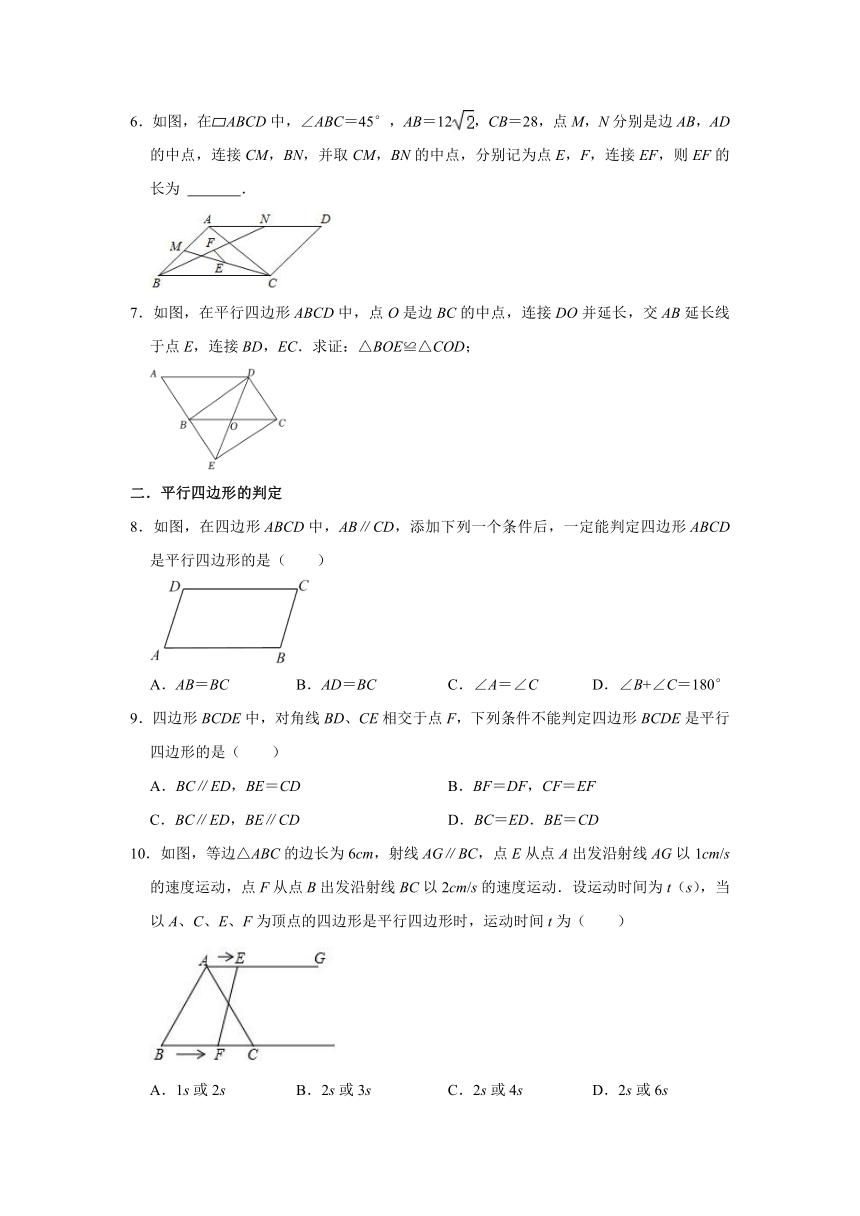
6.如图,在 ABCD中,∠ABC=45°,AB=12,CB=28,点M,N分别是边AB,AD的中点,连接CM,BN,并取CM,BN的中点,分别记为点E,F,连接EF,则EF的长为 .
7.如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.求证:△BOE≌△COD;
二.平行四边形的判定
8.如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=BC B.AD=BC C.∠A=∠C D.∠B+∠C=180°
9.四边形BCDE中,对角线BD、CE相交于点F,下列条件不能判定四边形BCDE是平行四边形的是( )
A.BC∥ED,BE=CD B.BF=DF,CF=EF
C.BC∥ED,BE∥CD D.BC=ED.BE=CD
10.如图,等边△ABC的边长为6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.设运动时间为t(s),当以A、C、E、F为顶点的四边形是平行四边形时,运动时间t为( )
A.1s或2s B.2s或3s C.2s或4s D.2s或6s
11.如图,点A、D、C、B在同一条直线上,AC=BD,AE=BF,AE∥BF.
求证:(1)△ADE≌△BCF;
(2)四边形DECF是平行四边形.
三.平行四边形的判定与性质
12.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
13.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
14.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,则四边形ABCD是平行四边形的理由是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
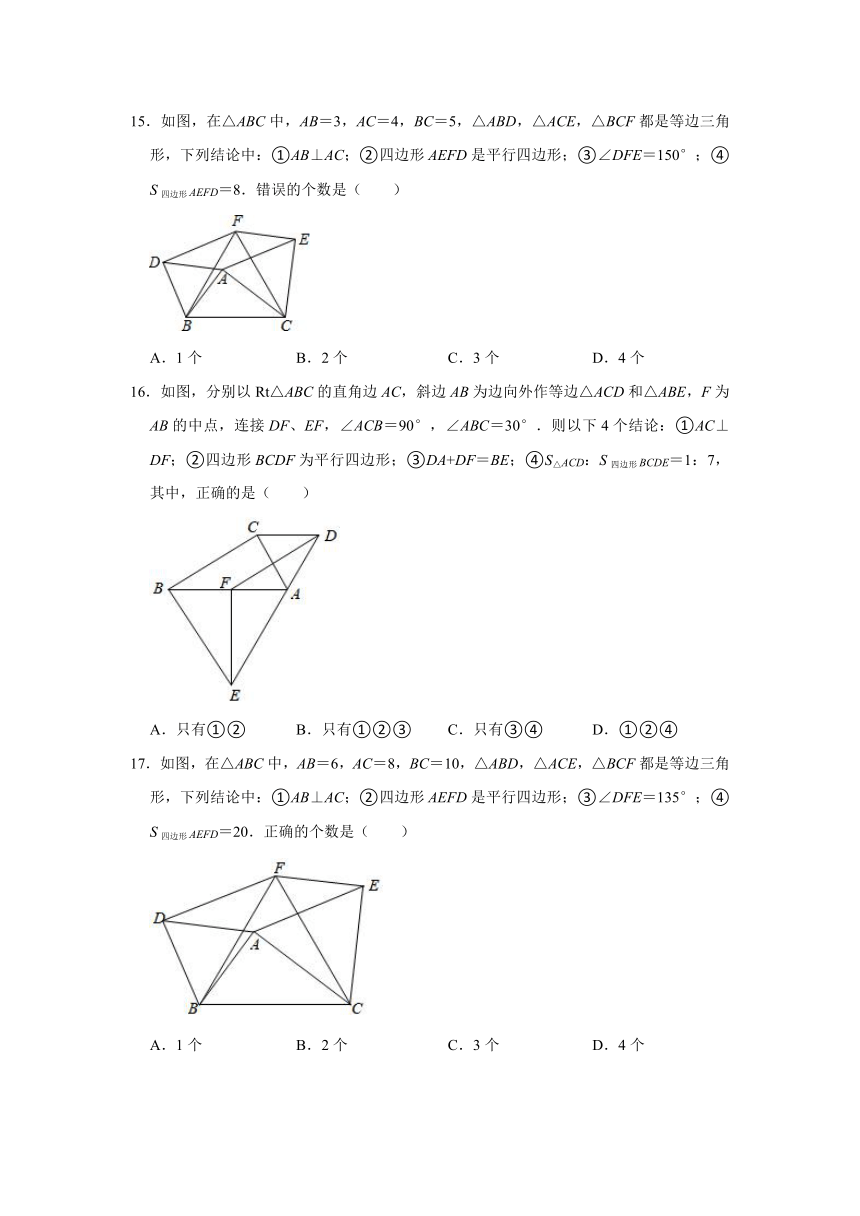
15.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
16.如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边△ACD和△ABE,F为AB的中点,连接DF、EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④S△ACD:S四边形BCDE=1:7,其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②④
17.如图,在△ABC中,AB=6,AC=8,BC=10,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A.1个 B.2个 C.3个 D.4个
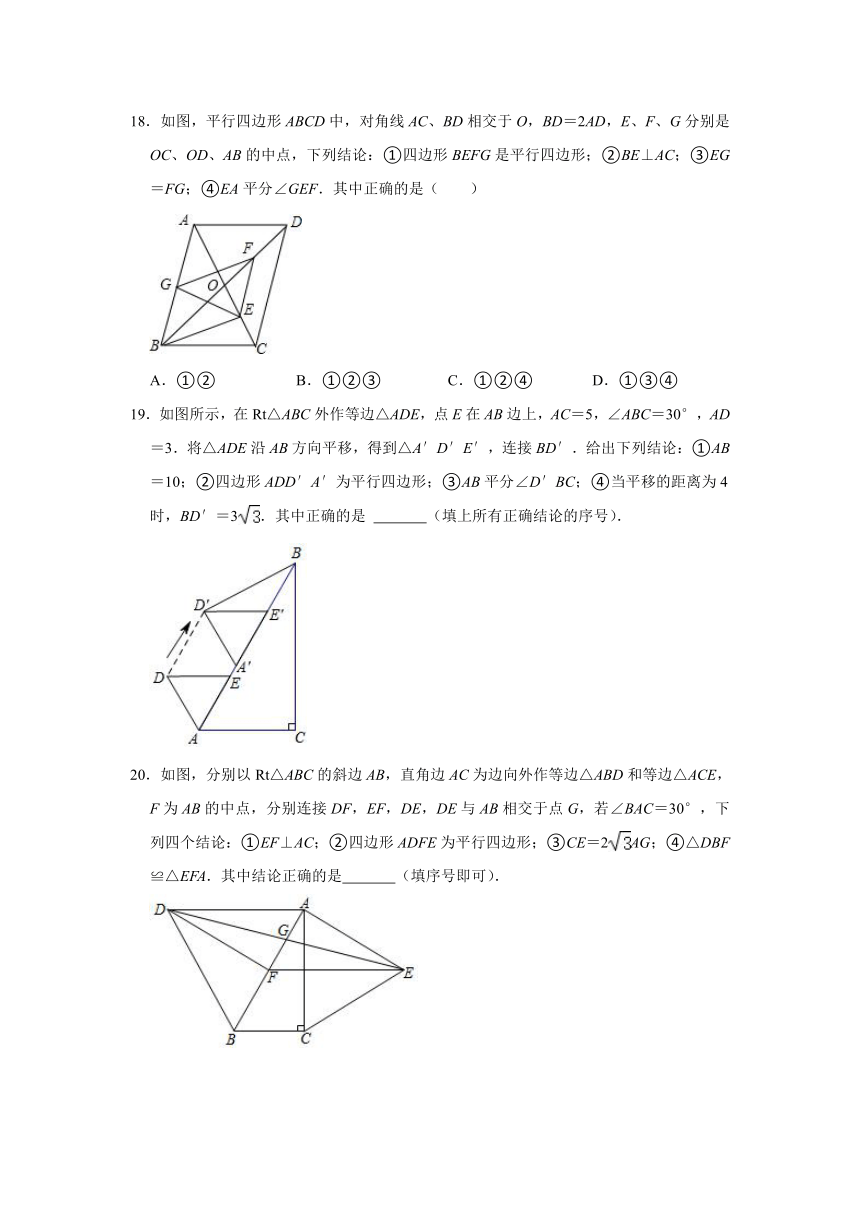
18.如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①四边形BEFG是平行四边形;②BE⊥AC;③EG=FG;④EA平分∠GEF.其中正确的是( )
A.①② B.①②③ C.①②④ D.①③④
19.如图所示,在Rt△ABC外作等边△ADE,点E在AB边上,AC=5,∠ABC=30°,AD=3.将△ADE沿AB方向平移,得到△A′D′E′,连接BD′.给出下列结论:①AB=10;②四边形ADD′A′为平行四边形;③AB平分∠D′BC;④当平移的距离为4时,BD′=3.其中正确的是 (填上所有正确结论的序号).
20.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,分别连接DF,EF,DE,DE与AB相交于点G,若∠BAC=30°,下列四个结论:①EF⊥AC;②四边形ADFE为平行四边形;③CE=2AG;④△DBF≌△EFA.其中结论正确的是 (填序号即可).
21.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
22.如图,△ABC是等边三角形,AD是BC边上的高.点E在AB的延长线上,连接ED,∠AED=30°,过A作AF⊥AB与ED的延长线交于点F,连接BF,CF,CE.
(1)求证:四边形BECF为平行四边形;
(2)若AB=6,请直接写出四边形BECF的周长.
23.如图,四边形ABCD中,点E在AD上,且EA=EB,∠ADB=∠CBD=90°,∠AEB+∠C=180°.
(1)求证:四边形BCDE是平行四边形.
(2)若AB=,DB=4.求四边形ABCD的面积.
24.如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,发现四边形ABDE是平行四边形.如图2,小华继续将图1中的纸片Rt△DEF沿AC方向平移,连接AE,BD,当点F与点C重合时停止平移.
请问:四边形ABDE是平行四边形吗?说明理由.
25.已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.
(1)如图1,求证:四边形ACEF是平行四边形;
(2)如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的倍.
26.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
27.在△ABC中,AB=AC,点P为△ABC为所在平面内一点,过点P分别作PF∥AC交AB于点F,PE∥AB交BC于点D,交AC于点E.
(1)当点P在BC边上(如图1)时,请探索线段PE,PF,AB之间的数量关系式为 .
(2)当点P在△ABC内(如图2)时,线段PD,PE,PF,AB之间有怎样的数量关系,请说明理由.
(3)当点P在△ABC外(如图3)时,线段PD,PE,PF,AB之间有怎样的数量关系,直接写出结论.
28.已知:如图,在 ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG=DH.
(1)若AC=6,BD=8,试求AD的取值范围;
(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;
(3)求证:四边形EHFG是平行四边形.
参考答案
一.平行四边形的性质
1.解:如图所示,过A作AH⊥BC于H,则∠AHB=90°,
∵∠ABC=60°,
∴在Rt△ABH中,AH=AB×sin60°=2×=,
∴S平行四边形ABCD=BC AH=3,
∵四边形ABCD是平行四边形,
∴AD∥BC,AO=CO,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴S△AOF=S△COE,
∴图中阴影部分的面积=×S ABCD=,
故选:C.
2.解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
,
∴△DCN≌△BAE(AAS),
∴BE=DN,AE=CN,
∵A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),
∴CN=AE=2﹣1=1,DN=BE=3,
∴DM=3﹣1=2,OM=2+1=3,
∴D的坐标为(3,2),
故选:B.
3.解:∵ ABCD的对角线AC,BD交于点O,
∴AO=CO,BO=DO,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,AE=CF,∠CFE=∠AEF,
又∵∠DOC=∠BOA,
∴选项①成立,选项②,③,④不一定成立,
故选:A.
4.解:①当△ABC是锐角三角形时,如图所示,过点A作AE⊥BC于E,
∵∠B=60°,AB=16,
∴BE=8,AE=8,
由勾股定理得,EC=,
∴BC=BE+EC=8+2=10,
∴ ABCD的周长=2(AB+BC)=2×(10+16)=52,
②当△ABC是锐角三角形时,如图所示,过点A作AE⊥BC于E,
由①可知,BE=8,EC=2,
∴BC=BE﹣EC=6,
∴ ABCD的周长=2(AB+BC)=2×(16+6)=44,
故答案为:52或44.
5.解:过E作EH⊥AB于H,在AB上取一点O,使得AO=DF=2,连接OF,OE.
∵△ABE是等边三角形,
∴AH=BH=AB=4,
∴HE=4,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AO=DF,AO∥DF,
∴四边形AOFD是平行四边形,
∴OF=AD=6,
∴当点F在OE上时,EF的值最小,
∵OE===2
∴EF的最小值=2﹣6
故答案为:2﹣6
6.解:如图,连接BE交CD于点G,连接GN,过点G作GH⊥DN于点H,
∵四边形ABCD是平行四边形,
∴AD=CB=28,CD=AB=12,
∵点M,N分别是边AB,AD的中点,
∴AN=DN=AD=14,BM=AB=6,
∵AB∥CD,
∴∠BME=∠GCE,∠MBE=∠CGE,
∵点E是CM的中点,
∴ME=CE,
在△MEB和△CEG中,
,
∴△MEB≌△CEG(AAS),
∴BE=GE,BM=GC=6,
∴DG=CD﹣GC=6,
∵∠D=∠ABC=45°,GH⊥DN,
∴DH=GH=DG=6,
∴NH=DN﹣DH=14﹣6=8,
∴GN===10,
∵BF=FN,BE=EG,
∴EF是△BGN的中位线,
∴EF=GN=5.
故答案为:5.
7.证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
二.平行四边形的判定
8.解:一定能判定四边形ABCD是平行四边形的是∠A=∠C,理由如下:
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
故选:C.
9.解:如图所示:
A、由BC∥ED,BE=CD,不能判定四边形BCDE是平行四边形,故选项A符合题意;
B、∵BF=DF,CF=EF,
∴四边形BCDE是平行四边形,故选项B不符合题意;
C、∵BC∥ED,BE∥CD,
∴四边形BCDE是平行四边形,故选项C不符合题意;
D、∵BC=ED.BE=CD,
∴四边形BCDE是平行四边形,故选项D不符合题意;
故选:A.
10.解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BC﹣BF=6﹣2t(cm),
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=6﹣2t,
解得:t=2;
②当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BF﹣BC=2t﹣6(cm),
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=2t﹣6,
解得:t=6;
综上可得:当t=2s或6s时,以A、C、E、F为顶点四边形是平行四边形.
故选:D.
11.证明:(1)∵AC=BD,
∴AC﹣CD=BD﹣CD,
即AD=BC,
∵AE∥BF,
∴∠A=∠B,
在△ADE与△BCF中,
,
∴△ADE≌△BCF(SAS);
(2)由(1)得:△ADE≌△BCF,
∴DE=CF,∠ADE=∠BCF,
∴∠EDC=∠FCD,
∴DE∥CF,
∴四边形DECF是平行四边形.
三.平行四边形的判定与性质
12.解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
13.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.
故选:B.
14.解:由题意可知,AB=CD,AD=BC,
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),
故选:B.
15.解:∵AB=3,AC=4,BC=5,32+42=52,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
过A作AG⊥DF于G,如图所示:
则∠AGD=90°,
∵四边形AEFD是平行四边形,
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴AG=AD=,
∴S AEFD=DF AG=4×=6,故④错误;
∴错误的个数是1个,
故选:A.
16.解:∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,AC=AB,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴CD∥AB,
∵F为AB的中点,
∴BF=AB,
∴BF∥AB,CD=BF,
∴四边形BCDF为平行四边形,故②正确;
∵四边形BCDF为平行四边形,
∴DF∥BC,
又∵∠ACB=90°,
∴AC⊥DF,故①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB,
∴DA+DF>BE,故③错误;
设AC=x,则AB=2x,
∴S△ACD=x2,S△ACB=x2,S△ABE=x2,
∴==,故④正确;
故选:D.
17.解:∵AB=6,AC=8,BC=10,62+82=102,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=8,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=6,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③错误;
过A作AG⊥DF于G,如图所示:
则∠AGD=90°,
∵四边形AEFD是平行四边形,
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴AG=AD=3,
∴S AEFD=DF AG=8×3=24,故④错误;
∴正确的个数是2个,
故选:B.
18.解:∵四边形ABCD是平行四边形,
∴BO=DO=BD,AD=BC,AB=CD,AB∥CD,
又∵BD=2AD,
∴OB=BC=OD=DA,
∵点E是OC中点,
∴BE⊥AC,故②正确;
∵E、F分别是OC、OD的中点,
∴EF是△OCD的中位线,
∴EF∥CD,EF=CD=AB,
∴EF∥AB,
∵点G是Rt△ABE斜边AB上的中点,
∴EG=AB=AG=BG,
∴EG=EF=AG=BG,
∴四边形BEFG是平行四边形,故①正确;
无法证明GE=GF,故③错误;
∵EF∥CD∥AB,
∴∠BAC=∠ACD=∠AEF,
∵AG=GE,
∴∠GAE=∠AEG,
∴∠AEG=∠AEF,
∴AE平分∠GEF,故④正确;
故选:C.
19.解:∵∠ACB=90°,AC=5,∠ABC=30°,
∴AB=2AC=10,故①正确;
由平移的性质得:A'D'=AD,A'D'∥AD,
∴四边形ADD′A′为平行四边形,故②正确;
当平移的距离为4时,EE'=4,
∴BE'=AB﹣AE﹣EE'=10﹣3﹣4=3,
由平移的性质得:∠A'D'E'=∠A'E'D'=∠AED=60°,A'D'=D'E'=DE=AD=3,
∴BE'=D'E',
∴∠E'BD'=∠E'D'B=∠A'E'D'=30°,
∴∠A'D'B=60°+30°=90°,
∴BD'=A'D'=3,故④正确;
由④得:当平移的距离为4时,∠E'BD'=∠ABC=30°,故③错误;
故答案为:①②④.
20.解:连接FC,如图所示:
∵∠ACB=90°,F为AB的中点,
∴FA=FB=FC,
∵△ACE是等边三角形,
∴EA=EC,
∵FA=FC,EA=EC,
∴点F、点E都在线段AC的垂直平分线上,
∴EF垂直平分AC,即EF⊥AC;故①正确;
∵△ABD和△ACE都是等边三角形,F为AB的中点,
∴DF⊥AB即∠DFA=90°,BD=DA=AB=2AF,∠DBA=∠DAB=∠EAC=∠ACE=60°.
∵∠BAC=30°,
∴∠DAC=∠EAF=90°,
∴∠DFA=∠EAF=90°,DA⊥AC,
∴DF∥AE,DA∥EF,
∴四边形ADFE为平行四边形;故②正确;
∵四边形ADFE为平行四边形,
∴AF=2AG,
∵△ACE是等边三角形,EF⊥AC,
∴AE=CE,∠AEF=30°,
∵∠EAF=90°,
∴EF=2AF=4AG,EF2=AF2+AE2,
∴(4AG)2=(2AG)2+CE2,
∴12AG2=CE2,
∴CE=2AG;故③正确;
∵四边形ADFE为平行四边形,
∴DA=EF,
∴BD=DA=EF,
在△DBF和△EFA中,
(SAS),
∴△DBF≌△EFA;故④正确;
故答案为:①②③④.
21.(1)证明:∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=CB,
又∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:设∠ABE=x,则∠DBF=2x,
由(1)得:四边形ABCD为平行四边形,
∴OB=OD,
∵EF⊥BD,
∴BE=DE,
∴∠EBD=∠EDB,
∵AD∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x,
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
∴100°+x+2x+2x=180°,
解得:x=16°,
即∠ABE=16°.
22.(1)证明:∵AD是等边△ABC的BC边上的高,
∴BD=DC,∠BAD=∠CAD=30°,
∵∠AED=30°,
∴ED=AD,∠ADF=∠AED+∠EAD=60°,
∵AF⊥AB,
∴∠DAF=90°﹣∠EAD=90°﹣30°=60°,
∴△ADF为等边三角形,
∴AD=DF,
∵ED=AD,
∴ED=DF,
∵BD=DC,
∴四边形BECF为平行四边形;
(2)∵AB=6,
∴BD=3,AD=3,
∵△ADF为等边三角形,
∴AF=AD=3,
∴BF===3,
∵∠ABC=60°,∠AED=30°,
∴∠BDE=30°,
∴BE=BD=3,
∴四边形BECF的周长为:2(BF+BE)=2(3+3)=6+6.
23.解:(1)∵∠ADB=∠CBD=90°,
∴DE∥CB,
∵∠AEB+∠C=180°,
∵∠AEB+∠BED=180°,
∴∠C=∠BED,
∴∠CDB=∠EBD,
∴BE∥CD,
∴四边形BEDC是平行四边形;
(2)∵四边形BEDC是平行四边形.
∴BC=DE,
在Rt△ABD中,由勾股定理得,
AD===8.
设DE=x,则EA=AD﹣DE=8﹣x,
∴EB=EA=8﹣x.
在Rt△BDE中,由勾股定理得,
DE2+DB2=EB2,
∴x2+42=(8﹣x)2.
解得x=3.
∴BC=DE=3,
∴S四边形ABCD=S△ABD+S△BDC=AD DB+DB BC=16+6=22.
24.(1)答:四边形ABDE是平行四边形.理由如下:
∵Rt△ABC≌Rt△DEF,
∴四边形ABDE是平行四边形;
25.(1)证明:∵BD=CD,BE=AE,
∴DE∥AC,
∴∠AEF=∠EAC,∠CED=∠ECA,
∵∠ACB=90°,BE=AE,
∴CE=AE,
∴∠EAC=∠ECA,
∵AF=AE,
∴∠F=∠AEF,
∴∠F=∠CED,
∴AF∥CE,
∴四边形ACEF是平行四边形;
(2)解:∵∠ACB=90°,∠B=30°,
∴AC=AB,
由(1)知CE=AB,
∴AC=CE=BE,
又∵四边形ACEF为平行四边形
∴四边形ACEF为菱形,
∴AE⊥CF,
∵CE=BE,
∴∠B=∠DCE=30°,
∴∠BED=∠BAC=60°,
∵DF∥AC,
∠BDE=∠ACB=∠CDE=90°,
∴BD=CD=DE,
∵∠DEB=∠FEG=∠CEG=60°,
∴∠CED=60°,
∴∠FEG=∠CED,
∵EF=CE,∠EGF=∠CDE=90°,
∴△EFG≌△CED(AAS),
∴EG=DE,FG=CD,
∴FG=DE,
∵CG=FG,
∴CG=DE,
∴等于线段DE的长度的倍的线段是FG,CG,CD,DB.
26.解:(1)BP=2t=2×3=6,
故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,
∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;
故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,
S△ABP=×BP×AB=×2t×4=4t;(0<t<4);
②当点P在CD上运动时,
S△ABP=×AB×BC=×4×8=16;(4≤t≤6);
③当点P在AD上运动时,
S△ABP=×AB×AP=×4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,
∴点P到AB边的距离也为4,
即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,
∴点P到DE边的距离也为4,
∴PE=DE=5,
∴PC=PE﹣CE=2,
∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,
即PC=PH,
∵PC=2t﹣8,
∵S△DCE=S△DPE+S△PCE,
∴3×4=5×PH+3×PC,
∴12=8PH,
∴12=8(2t﹣8),
解得t=.
综上所述:t=2或t=3或t=时,点P到四边形ABED相邻两边距离相等.
27.解:(1)答:PE+PF=AB.
证明如下:∵点P在BC上,
∴PD=0,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PF=AE,
∵PE∥AC,
∴∠BPE=∠C,
∴∠B=∠BPE,
∴PE=BE,
∴PE+PF=BE+AE=AB,
∵PD=0,
∴PE+PF=AB;
故答案为:PE+PF=AB
(2)证明:∵AB=AC,
∴∠B=∠C,
∵PE∥AB,
∴∠B=∠CDE,
∴∠C=∠CDE,
∴CE=PD+PE,
∵PF∥AC,PE∥AB,
∴四边形PFAE是平行四边形,
∴PE=AF,
∴PD+PE+PF=AC,
∴PD+PE+PF=AB;
(3)证明:同(2)可证DE=CE,PE=AF,
∵AE+CE=AC,
∴PF+PE﹣PD=AC,
∴PE+PF﹣PD=AB.
28.解:(1)∵四边形ABCD是平行四边形,
∴OA=AC=3,OD=BD=4,
∴1<AD<7.
(2)∵CA=AD,∠CAD=50°,
∴∠ADC=∠ACD=(180°﹣50°)=65°,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=65°.
(3)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴AE=CF,BG=DH,
∴OE=OF,OG=OH,
∴四边形EHFG是平行四边形.
一.平行四边形的性质
1.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积为( )
A.1.5 B. C. D.
2.如图,已知 ABCD三个顶点坐标是A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),那么第四个顶点D的坐标是( )
A.(3,1) B.(3,2) C.(3,3) D.(3,4)
3.如图,点O是 ABCD对角线的交点,EF过点O分别交AD,BC于点E,F.下列结论:①OE=OF;②AE=BF;③∠DOC=∠OCD;④∠CFE=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
4.在 ABCD中,若∠B=60°,AB=16,AC=14,则 ABCD的周长是 .
5.如图,在平行四边形ABCD中,AB=8,AD=6,以AB为边向右作等边△ABE,F为边CD上一点,DF=2,连接EF,则EF的最小值为 .
6.如图,在 ABCD中,∠ABC=45°,AB=12,CB=28,点M,N分别是边AB,AD的中点,连接CM,BN,并取CM,BN的中点,分别记为点E,F,连接EF,则EF的长为 .
7.如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.求证:△BOE≌△COD;
二.平行四边形的判定
8.如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=BC B.AD=BC C.∠A=∠C D.∠B+∠C=180°
9.四边形BCDE中,对角线BD、CE相交于点F,下列条件不能判定四边形BCDE是平行四边形的是( )
A.BC∥ED,BE=CD B.BF=DF,CF=EF
C.BC∥ED,BE∥CD D.BC=ED.BE=CD
10.如图,等边△ABC的边长为6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.设运动时间为t(s),当以A、C、E、F为顶点的四边形是平行四边形时,运动时间t为( )
A.1s或2s B.2s或3s C.2s或4s D.2s或6s
11.如图,点A、D、C、B在同一条直线上,AC=BD,AE=BF,AE∥BF.
求证:(1)△ADE≌△BCF;
(2)四边形DECF是平行四边形.
三.平行四边形的判定与性质
12.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
13.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
14.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,则四边形ABCD是平行四边形的理由是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
15.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
16.如图,分别以Rt△ABC的直角边AC,斜边AB为边向外作等边△ACD和△ABE,F为AB的中点,连接DF、EF,∠ACB=90°,∠ABC=30°.则以下4个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④S△ACD:S四边形BCDE=1:7,其中,正确的是( )
A.只有①② B.只有①②③ C.只有③④ D.①②④
17.如图,在△ABC中,AB=6,AC=8,BC=10,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=135°;④S四边形AEFD=20.正确的个数是( )
A.1个 B.2个 C.3个 D.4个
18.如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①四边形BEFG是平行四边形;②BE⊥AC;③EG=FG;④EA平分∠GEF.其中正确的是( )
A.①② B.①②③ C.①②④ D.①③④
19.如图所示,在Rt△ABC外作等边△ADE,点E在AB边上,AC=5,∠ABC=30°,AD=3.将△ADE沿AB方向平移,得到△A′D′E′,连接BD′.给出下列结论:①AB=10;②四边形ADD′A′为平行四边形;③AB平分∠D′BC;④当平移的距离为4时,BD′=3.其中正确的是 (填上所有正确结论的序号).
20.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,分别连接DF,EF,DE,DE与AB相交于点G,若∠BAC=30°,下列四个结论:①EF⊥AC;②四边形ADFE为平行四边形;③CE=2AG;④△DBF≌△EFA.其中结论正确的是 (填序号即可).
21.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
22.如图,△ABC是等边三角形,AD是BC边上的高.点E在AB的延长线上,连接ED,∠AED=30°,过A作AF⊥AB与ED的延长线交于点F,连接BF,CF,CE.
(1)求证:四边形BECF为平行四边形;
(2)若AB=6,请直接写出四边形BECF的周长.
23.如图,四边形ABCD中,点E在AD上,且EA=EB,∠ADB=∠CBD=90°,∠AEB+∠C=180°.
(1)求证:四边形BCDE是平行四边形.
(2)若AB=,DB=4.求四边形ABCD的面积.
24.如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,发现四边形ABDE是平行四边形.如图2,小华继续将图1中的纸片Rt△DEF沿AC方向平移,连接AE,BD,当点F与点C重合时停止平移.
请问:四边形ABDE是平行四边形吗?说明理由.
25.已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.
(1)如图1,求证:四边形ACEF是平行四边形;
(2)如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的倍.
26.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
27.在△ABC中,AB=AC,点P为△ABC为所在平面内一点,过点P分别作PF∥AC交AB于点F,PE∥AB交BC于点D,交AC于点E.
(1)当点P在BC边上(如图1)时,请探索线段PE,PF,AB之间的数量关系式为 .
(2)当点P在△ABC内(如图2)时,线段PD,PE,PF,AB之间有怎样的数量关系,请说明理由.
(3)当点P在△ABC外(如图3)时,线段PD,PE,PF,AB之间有怎样的数量关系,直接写出结论.
28.已知:如图,在 ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG=DH.
(1)若AC=6,BD=8,试求AD的取值范围;
(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;
(3)求证:四边形EHFG是平行四边形.
参考答案
一.平行四边形的性质
1.解:如图所示,过A作AH⊥BC于H,则∠AHB=90°,
∵∠ABC=60°,
∴在Rt△ABH中,AH=AB×sin60°=2×=,
∴S平行四边形ABCD=BC AH=3,
∵四边形ABCD是平行四边形,
∴AD∥BC,AO=CO,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴S△AOF=S△COE,
∴图中阴影部分的面积=×S ABCD=,
故选:C.
2.解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
,
∴△DCN≌△BAE(AAS),
∴BE=DN,AE=CN,
∵A(﹣1,0)、B(﹣2,﹣3)、C(2,﹣1),
∴CN=AE=2﹣1=1,DN=BE=3,
∴DM=3﹣1=2,OM=2+1=3,
∴D的坐标为(3,2),
故选:B.
3.解:∵ ABCD的对角线AC,BD交于点O,
∴AO=CO,BO=DO,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,AE=CF,∠CFE=∠AEF,
又∵∠DOC=∠BOA,
∴选项①成立,选项②,③,④不一定成立,
故选:A.
4.解:①当△ABC是锐角三角形时,如图所示,过点A作AE⊥BC于E,
∵∠B=60°,AB=16,
∴BE=8,AE=8,
由勾股定理得,EC=,
∴BC=BE+EC=8+2=10,
∴ ABCD的周长=2(AB+BC)=2×(10+16)=52,
②当△ABC是锐角三角形时,如图所示,过点A作AE⊥BC于E,
由①可知,BE=8,EC=2,
∴BC=BE﹣EC=6,
∴ ABCD的周长=2(AB+BC)=2×(16+6)=44,
故答案为:52或44.
5.解:过E作EH⊥AB于H,在AB上取一点O,使得AO=DF=2,连接OF,OE.
∵△ABE是等边三角形,
∴AH=BH=AB=4,
∴HE=4,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AO=DF,AO∥DF,
∴四边形AOFD是平行四边形,
∴OF=AD=6,
∴当点F在OE上时,EF的值最小,
∵OE===2
∴EF的最小值=2﹣6
故答案为:2﹣6
6.解:如图,连接BE交CD于点G,连接GN,过点G作GH⊥DN于点H,
∵四边形ABCD是平行四边形,
∴AD=CB=28,CD=AB=12,
∵点M,N分别是边AB,AD的中点,
∴AN=DN=AD=14,BM=AB=6,
∵AB∥CD,
∴∠BME=∠GCE,∠MBE=∠CGE,
∵点E是CM的中点,
∴ME=CE,
在△MEB和△CEG中,
,
∴△MEB≌△CEG(AAS),
∴BE=GE,BM=GC=6,
∴DG=CD﹣GC=6,
∵∠D=∠ABC=45°,GH⊥DN,
∴DH=GH=DG=6,
∴NH=DN﹣DH=14﹣6=8,
∴GN===10,
∵BF=FN,BE=EG,
∴EF是△BGN的中位线,
∴EF=GN=5.
故答案为:5.
7.证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
二.平行四边形的判定
8.解:一定能判定四边形ABCD是平行四边形的是∠A=∠C,理由如下:
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
故选:C.
9.解:如图所示:
A、由BC∥ED,BE=CD,不能判定四边形BCDE是平行四边形,故选项A符合题意;
B、∵BF=DF,CF=EF,
∴四边形BCDE是平行四边形,故选项B不符合题意;
C、∵BC∥ED,BE∥CD,
∴四边形BCDE是平行四边形,故选项C不符合题意;
D、∵BC=ED.BE=CD,
∴四边形BCDE是平行四边形,故选项D不符合题意;
故选:A.
10.解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BC﹣BF=6﹣2t(cm),
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=6﹣2t,
解得:t=2;
②当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BF﹣BC=2t﹣6(cm),
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=2t﹣6,
解得:t=6;
综上可得:当t=2s或6s时,以A、C、E、F为顶点四边形是平行四边形.
故选:D.
11.证明:(1)∵AC=BD,
∴AC﹣CD=BD﹣CD,
即AD=BC,
∵AE∥BF,
∴∠A=∠B,
在△ADE与△BCF中,
,
∴△ADE≌△BCF(SAS);
(2)由(1)得:△ADE≌△BCF,
∴DE=CF,∠ADE=∠BCF,
∴∠EDC=∠FCD,
∴DE∥CF,
∴四边形DECF是平行四边形.
三.平行四边形的判定与性质
12.解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
13.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.
故选:B.
14.解:由题意可知,AB=CD,AD=BC,
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),
故选:B.
15.解:∵AB=3,AC=4,BC=5,32+42=52,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
过A作AG⊥DF于G,如图所示:
则∠AGD=90°,
∵四边形AEFD是平行四边形,
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴AG=AD=,
∴S AEFD=DF AG=4×=6,故④错误;
∴错误的个数是1个,
故选:A.
16.解:∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,AC=AB,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴CD∥AB,
∵F为AB的中点,
∴BF=AB,
∴BF∥AB,CD=BF,
∴四边形BCDF为平行四边形,故②正确;
∵四边形BCDF为平行四边形,
∴DF∥BC,
又∵∠ACB=90°,
∴AC⊥DF,故①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB,
∴DA+DF>BE,故③错误;
设AC=x,则AB=2x,
∴S△ACD=x2,S△ACB=x2,S△ABE=x2,
∴==,故④正确;
故选:D.
17.解:∵AB=6,AC=8,BC=10,62+82=102,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=8,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=6,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③错误;
过A作AG⊥DF于G,如图所示:
则∠AGD=90°,
∵四边形AEFD是平行四边形,
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴AG=AD=3,
∴S AEFD=DF AG=8×3=24,故④错误;
∴正确的个数是2个,
故选:B.
18.解:∵四边形ABCD是平行四边形,
∴BO=DO=BD,AD=BC,AB=CD,AB∥CD,
又∵BD=2AD,
∴OB=BC=OD=DA,
∵点E是OC中点,
∴BE⊥AC,故②正确;
∵E、F分别是OC、OD的中点,
∴EF是△OCD的中位线,
∴EF∥CD,EF=CD=AB,
∴EF∥AB,
∵点G是Rt△ABE斜边AB上的中点,
∴EG=AB=AG=BG,
∴EG=EF=AG=BG,
∴四边形BEFG是平行四边形,故①正确;
无法证明GE=GF,故③错误;
∵EF∥CD∥AB,
∴∠BAC=∠ACD=∠AEF,
∵AG=GE,
∴∠GAE=∠AEG,
∴∠AEG=∠AEF,
∴AE平分∠GEF,故④正确;
故选:C.
19.解:∵∠ACB=90°,AC=5,∠ABC=30°,
∴AB=2AC=10,故①正确;
由平移的性质得:A'D'=AD,A'D'∥AD,
∴四边形ADD′A′为平行四边形,故②正确;
当平移的距离为4时,EE'=4,
∴BE'=AB﹣AE﹣EE'=10﹣3﹣4=3,
由平移的性质得:∠A'D'E'=∠A'E'D'=∠AED=60°,A'D'=D'E'=DE=AD=3,
∴BE'=D'E',
∴∠E'BD'=∠E'D'B=∠A'E'D'=30°,
∴∠A'D'B=60°+30°=90°,
∴BD'=A'D'=3,故④正确;
由④得:当平移的距离为4时,∠E'BD'=∠ABC=30°,故③错误;
故答案为:①②④.
20.解:连接FC,如图所示:
∵∠ACB=90°,F为AB的中点,
∴FA=FB=FC,
∵△ACE是等边三角形,
∴EA=EC,
∵FA=FC,EA=EC,
∴点F、点E都在线段AC的垂直平分线上,
∴EF垂直平分AC,即EF⊥AC;故①正确;
∵△ABD和△ACE都是等边三角形,F为AB的中点,
∴DF⊥AB即∠DFA=90°,BD=DA=AB=2AF,∠DBA=∠DAB=∠EAC=∠ACE=60°.
∵∠BAC=30°,
∴∠DAC=∠EAF=90°,
∴∠DFA=∠EAF=90°,DA⊥AC,
∴DF∥AE,DA∥EF,
∴四边形ADFE为平行四边形;故②正确;
∵四边形ADFE为平行四边形,
∴AF=2AG,
∵△ACE是等边三角形,EF⊥AC,
∴AE=CE,∠AEF=30°,
∵∠EAF=90°,
∴EF=2AF=4AG,EF2=AF2+AE2,
∴(4AG)2=(2AG)2+CE2,
∴12AG2=CE2,
∴CE=2AG;故③正确;
∵四边形ADFE为平行四边形,
∴DA=EF,
∴BD=DA=EF,
在△DBF和△EFA中,
(SAS),
∴△DBF≌△EFA;故④正确;
故答案为:①②③④.
21.(1)证明:∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=CB,
又∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:设∠ABE=x,则∠DBF=2x,
由(1)得:四边形ABCD为平行四边形,
∴OB=OD,
∵EF⊥BD,
∴BE=DE,
∴∠EBD=∠EDB,
∵AD∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x,
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
∴100°+x+2x+2x=180°,
解得:x=16°,
即∠ABE=16°.
22.(1)证明:∵AD是等边△ABC的BC边上的高,
∴BD=DC,∠BAD=∠CAD=30°,
∵∠AED=30°,
∴ED=AD,∠ADF=∠AED+∠EAD=60°,
∵AF⊥AB,
∴∠DAF=90°﹣∠EAD=90°﹣30°=60°,
∴△ADF为等边三角形,
∴AD=DF,
∵ED=AD,
∴ED=DF,
∵BD=DC,
∴四边形BECF为平行四边形;
(2)∵AB=6,
∴BD=3,AD=3,
∵△ADF为等边三角形,
∴AF=AD=3,
∴BF===3,
∵∠ABC=60°,∠AED=30°,
∴∠BDE=30°,
∴BE=BD=3,
∴四边形BECF的周长为:2(BF+BE)=2(3+3)=6+6.
23.解:(1)∵∠ADB=∠CBD=90°,
∴DE∥CB,
∵∠AEB+∠C=180°,
∵∠AEB+∠BED=180°,
∴∠C=∠BED,
∴∠CDB=∠EBD,
∴BE∥CD,
∴四边形BEDC是平行四边形;
(2)∵四边形BEDC是平行四边形.
∴BC=DE,
在Rt△ABD中,由勾股定理得,
AD===8.
设DE=x,则EA=AD﹣DE=8﹣x,
∴EB=EA=8﹣x.
在Rt△BDE中,由勾股定理得,
DE2+DB2=EB2,
∴x2+42=(8﹣x)2.
解得x=3.
∴BC=DE=3,
∴S四边形ABCD=S△ABD+S△BDC=AD DB+DB BC=16+6=22.
24.(1)答:四边形ABDE是平行四边形.理由如下:
∵Rt△ABC≌Rt△DEF,
∴四边形ABDE是平行四边形;
25.(1)证明:∵BD=CD,BE=AE,
∴DE∥AC,
∴∠AEF=∠EAC,∠CED=∠ECA,
∵∠ACB=90°,BE=AE,
∴CE=AE,
∴∠EAC=∠ECA,
∵AF=AE,
∴∠F=∠AEF,
∴∠F=∠CED,
∴AF∥CE,
∴四边形ACEF是平行四边形;
(2)解:∵∠ACB=90°,∠B=30°,
∴AC=AB,
由(1)知CE=AB,
∴AC=CE=BE,
又∵四边形ACEF为平行四边形
∴四边形ACEF为菱形,
∴AE⊥CF,
∵CE=BE,
∴∠B=∠DCE=30°,
∴∠BED=∠BAC=60°,
∵DF∥AC,
∠BDE=∠ACB=∠CDE=90°,
∴BD=CD=DE,
∵∠DEB=∠FEG=∠CEG=60°,
∴∠CED=60°,
∴∠FEG=∠CED,
∵EF=CE,∠EGF=∠CDE=90°,
∴△EFG≌△CED(AAS),
∴EG=DE,FG=CD,
∴FG=DE,
∵CG=FG,
∴CG=DE,
∴等于线段DE的长度的倍的线段是FG,CG,CD,DB.
26.解:(1)BP=2t=2×3=6,
故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,
∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;
故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,
S△ABP=×BP×AB=×2t×4=4t;(0<t<4);
②当点P在CD上运动时,
S△ABP=×AB×BC=×4×8=16;(4≤t≤6);
③当点P在AD上运动时,
S△ABP=×AB×AP=×4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,
∴点P到AB边的距离也为4,
即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,
∴点P到DE边的距离也为4,
∴PE=DE=5,
∴PC=PE﹣CE=2,
∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,
即PC=PH,
∵PC=2t﹣8,
∵S△DCE=S△DPE+S△PCE,
∴3×4=5×PH+3×PC,
∴12=8PH,
∴12=8(2t﹣8),
解得t=.
综上所述:t=2或t=3或t=时,点P到四边形ABED相邻两边距离相等.
27.解:(1)答:PE+PF=AB.
证明如下:∵点P在BC上,
∴PD=0,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PF=AE,
∵PE∥AC,
∴∠BPE=∠C,
∴∠B=∠BPE,
∴PE=BE,
∴PE+PF=BE+AE=AB,
∵PD=0,
∴PE+PF=AB;
故答案为:PE+PF=AB
(2)证明:∵AB=AC,
∴∠B=∠C,
∵PE∥AB,
∴∠B=∠CDE,
∴∠C=∠CDE,
∴CE=PD+PE,
∵PF∥AC,PE∥AB,
∴四边形PFAE是平行四边形,
∴PE=AF,
∴PD+PE+PF=AC,
∴PD+PE+PF=AB;
(3)证明:同(2)可证DE=CE,PE=AF,
∵AE+CE=AC,
∴PF+PE﹣PD=AC,
∴PE+PF﹣PD=AB.
28.解:(1)∵四边形ABCD是平行四边形,
∴OA=AC=3,OD=BD=4,
∴1<AD<7.
(2)∵CA=AD,∠CAD=50°,
∴∠ADC=∠ACD=(180°﹣50°)=65°,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=65°.
(3)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴AE=CF,BG=DH,
∴OE=OF,OG=OH,
∴四边形EHFG是平行四边形.
