19.1多边形内角和同步练习(含解析)沪科版数学八年级下册
文档属性
| 名称 | 19.1多边形内角和同步练习(含解析)沪科版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 783.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 00:00:00 | ||
图片预览


文档简介
多边形内角和
一、单选题
1.十二边形的内角和为( )
A. B. C. D.无法计算
2.一个多边形的每个内角均为,则这个多边形是( )
A.八边形 B.六边形 C.五边形 D.四边形
3.如果一个多边形的内角和等于一个三角形的外角和,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.如图,四边形中,,与,相邻的两外角的平分线交于点,若,则的度数为( )
A. B. C. D.
5.图中表示被撕掉一块的正n边形纸片,若a⊥b,则n的值是( )
A.6 B.8 C.10 D.12
6.若一个多边形的每一个外角都是,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
7.将一个多边形切去一个角后所得的多边形内角和为,则原多边形的边数为( )
A.或 B.或 C.或或 D.或或
8.一块四边形玻璃被打破,如图所示.小红想制做一模一样的玻璃,经测量,,则的度数( )
A. B. C. D.
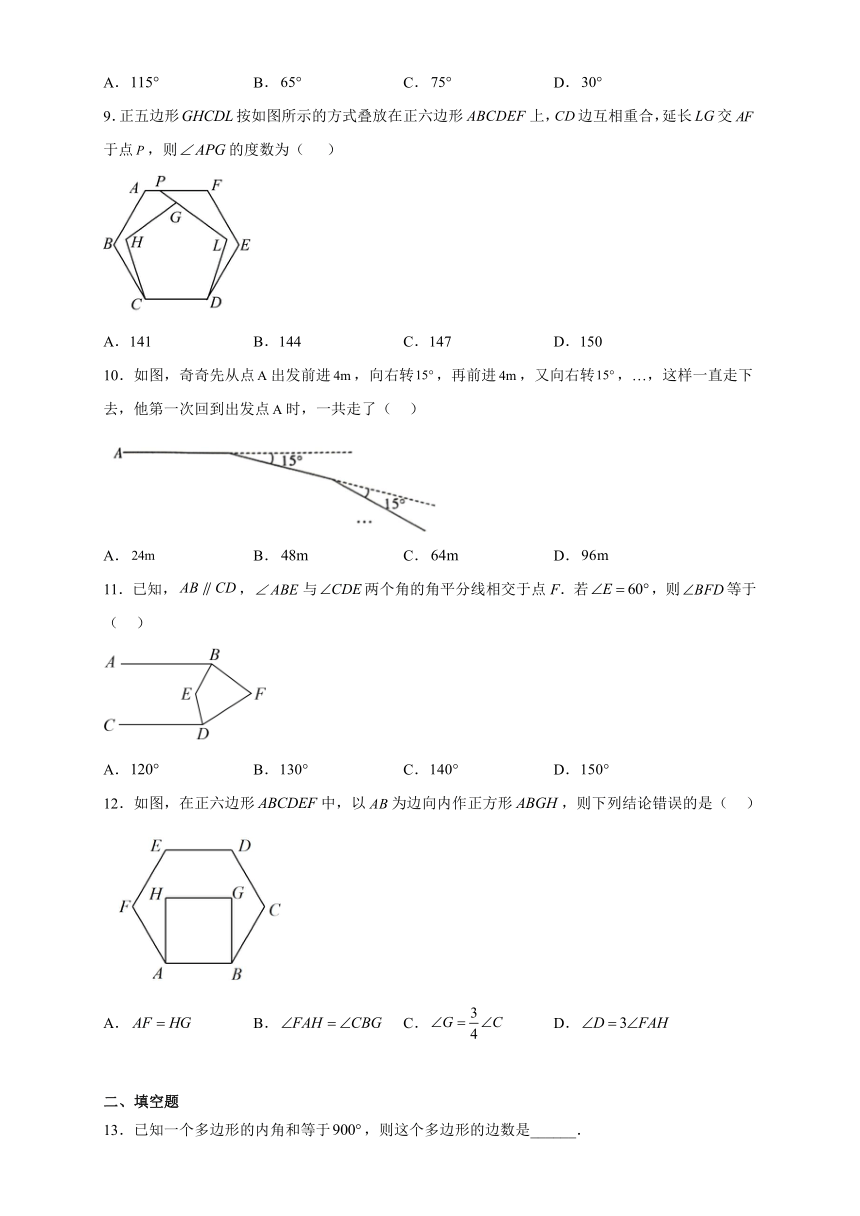
9.正五边形按如图所示的方式叠放在正六边形上,边互相重合,延长交于点,则的度数为( )
A.141 B.144 C.147 D.150
10.如图,奇奇先从点出发前进,向右转,再前进,又向右转,…,这样一直走下去,他第一次回到出发点时,一共走了( )
A. B. C. D.
11.已知,,与两个角的角平分线相交于点F.若,则等于( )
A. B. C. D.
12.如图,在正六边形中,以为边向内作正方形,则下列结论错误的是( )
A. B. C. D.
二、填空题
13.已知一个多边形的内角和等于,则这个多边形的边数是______.
14.当一个多边形边数增加2时,它的内角和增加了______.
15.一个凸多边形恰好有三个内角是钝角,这个多边形的边数的最大值是________.
16.如图,在正五边形中,连接交于点F,则的度数为______°.
17.正五边形和正方形位置如图所示,连接,则的度数为______.
三、解答题
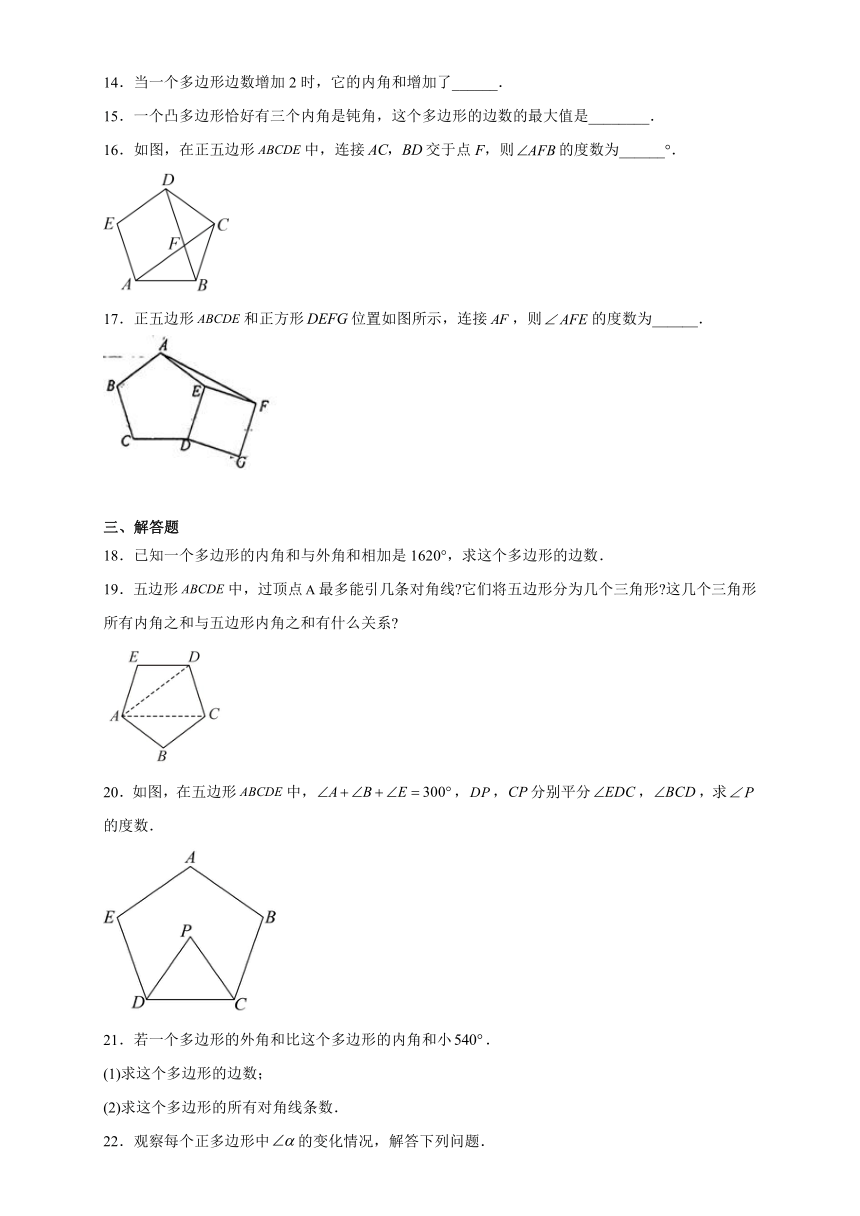
18.已知一个多边形的内角和与外角和相加是1620°,求这个多边形的边数.
19.五边形中,过顶点最多能引几条对角线 它们将五边形分为几个三角形 这几个三角形所有内角之和与五边形内角之和有什么关系
20.如图,在五边形中,,,分别平分,,求的度数.
21.若一个多边形的外角和比这个多边形的内角和小.
(1)求这个多边形的边数;
(2)求这个多边形的所有对角线条数.
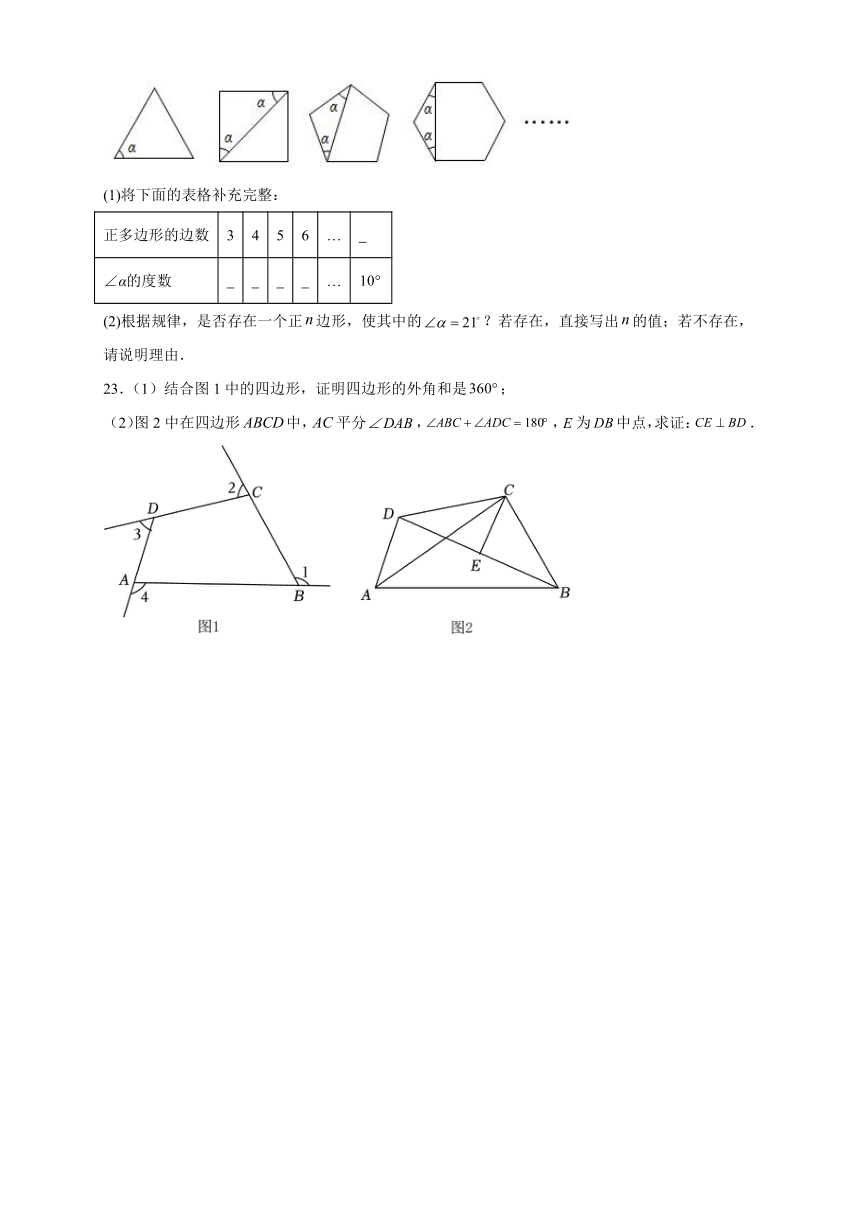
22.观察每个正多边形中的变化情况,解答下列问题.
(1)将下面的表格补充完整:
正多边形的边数 3 4 5 6 …
∠α的度数 …
(2)根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.
23.(1)结合图1中的四边形,证明四边形的外角和是;
(2)图2中在四边形中,平分,,为中点,求证:.
参考答案
1.C
解:十二边形的内角和为,
故选C.
2.B
解:根据题意该多边形每个外角是,
,则这个多边形是六边形.
故选:B.
3.B
解:设这个多边形边数是n,根据题意得:
,
解得:,
即这个多边形是四边形,故B正确.
故选:B.
4.C
解:如图,连接并延长,
,,
,
、相邻的两外角平分线交于点,
,
,,
即
.
故选:.
5.B
解:如图,延长 ,交于点,
,
,
正多边形的一个外角为,
.
故选:B.
6.D
解:∵一个多边形的每一个外角都是,
∴这个多边形的边数为,
故选:D.
7.C
解:多边形的内角和可以表示成(且n是正整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,
根据题意得,
解得:,
则多边形的边数是或或,故C正确.
故选:C.
8.D
解:∵,,四边形内角和为360度,
∴,
故选:D.
9.B
解:如图,延长交于,
∵正五边形的内角和为,正六边形的内角和为,多边形的外角和为,
∴正六边形的一个内角和外角分别为、,正五边形的一个内角和外角分别为、,
∴,,,
在五边形中,,
∴,
在五边形中,,
故选:B.
10.D
解:∵奇奇从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为,
则一共走了米.
故选D.
11.D
解:过点E作,
∵、分别是和的平分线,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选D.
12.D
解:∵在正六边形和正方形中,
∴,,
∴,故A选项正确,不符合题意;
∵在正六边形和正方形中,
∴,,
∴,故B选项正确,不符合题意;
∵多边形是正六边形,
∴该多边形内角和为:,
∴,
∵多边形是正方形,
∴该多边形内角和为:,
∴,
∴,故C选项正确,不符合题意;
∵,
∴,故D选项不正确,符合题意
故选:D.
13.
解:设这个多边形边数为,
依题意,得:,
解得:,
∴这个多边形的边数是7.
故答案为:.
14.
解:n边形的内角和是,
边数增加2,则新的多边形的内角和是.
∵.
故它的内角和增加.
故答案为:.
15.6
解:设个多边形边数为n,三个钝角分别为,
∵,,,
∴,
∵该凸多边形恰好有三个内角是钝角,
∴凸多边形恰好有个锐角,
根据锐角的定义可得:所有的锐角和,
∴该多边形的内角和,
解得:,
∵n为整数,
∴n的最大值为6.
16.72
解:∵五边形为正五边形,
∴,,
∴,
∴.
故答案为:72.
17.
解:∵正五边形,
∴,
∵正方形,
∴,
∴,
∵,
∴.
故答案为:.
18.9
解:设这个多边形的边数为n,
由题意得:,
解得,
∴这个多边形的边数为9.
19.2条,3个,这几个三角形所有内角之和与五边形内角之和相等
解:五边形中,过顶点最多能引2条对角线,它们将五边形分为3个三角形,这几个三角形所有内角之和与五边形内角之和相等.
20.
解:五边形的内角和等于,,
;
,分别平分,,
,
;
故答案为:.
21.(1)这个多边形的边数是7
(2)14条
(1)解:设这个多边形的边数为n,
,
解得.
即这个多边形的边数是7.
(2)解:,
即这个多边形有14条对角线.
22.(1);;;;18;
(2)不存在,理由见解析
(1)解:填表如下:
正多边形的边数 3 4 5 6 18
的度数
故答案为:,,,,18;
(2)解:不存在,理由如下:
假设存在正 边形使得,得,
解得:,又是正整数,
所以不存在正边形使得.
23.(1)见解析;(2)见解析
证明:(1),,,,
,
四边形的内角和是,
,
四边形的外角和是;
(2)过点作交于点,过点作交延长线于点,
,,
,
平分,
,
,
,
,
为中点,
.
一、单选题
1.十二边形的内角和为( )
A. B. C. D.无法计算
2.一个多边形的每个内角均为,则这个多边形是( )
A.八边形 B.六边形 C.五边形 D.四边形
3.如果一个多边形的内角和等于一个三角形的外角和,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.如图,四边形中,,与,相邻的两外角的平分线交于点,若,则的度数为( )
A. B. C. D.
5.图中表示被撕掉一块的正n边形纸片,若a⊥b,则n的值是( )
A.6 B.8 C.10 D.12
6.若一个多边形的每一个外角都是,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
7.将一个多边形切去一个角后所得的多边形内角和为,则原多边形的边数为( )
A.或 B.或 C.或或 D.或或
8.一块四边形玻璃被打破,如图所示.小红想制做一模一样的玻璃,经测量,,则的度数( )
A. B. C. D.
9.正五边形按如图所示的方式叠放在正六边形上,边互相重合,延长交于点,则的度数为( )
A.141 B.144 C.147 D.150
10.如图,奇奇先从点出发前进,向右转,再前进,又向右转,…,这样一直走下去,他第一次回到出发点时,一共走了( )
A. B. C. D.
11.已知,,与两个角的角平分线相交于点F.若,则等于( )
A. B. C. D.
12.如图,在正六边形中,以为边向内作正方形,则下列结论错误的是( )
A. B. C. D.
二、填空题
13.已知一个多边形的内角和等于,则这个多边形的边数是______.
14.当一个多边形边数增加2时,它的内角和增加了______.
15.一个凸多边形恰好有三个内角是钝角,这个多边形的边数的最大值是________.
16.如图,在正五边形中,连接交于点F,则的度数为______°.
17.正五边形和正方形位置如图所示,连接,则的度数为______.
三、解答题
18.已知一个多边形的内角和与外角和相加是1620°,求这个多边形的边数.
19.五边形中,过顶点最多能引几条对角线 它们将五边形分为几个三角形 这几个三角形所有内角之和与五边形内角之和有什么关系
20.如图,在五边形中,,,分别平分,,求的度数.
21.若一个多边形的外角和比这个多边形的内角和小.
(1)求这个多边形的边数;
(2)求这个多边形的所有对角线条数.
22.观察每个正多边形中的变化情况,解答下列问题.
(1)将下面的表格补充完整:
正多边形的边数 3 4 5 6 …
∠α的度数 …
(2)根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.
23.(1)结合图1中的四边形,证明四边形的外角和是;
(2)图2中在四边形中,平分,,为中点,求证:.
参考答案
1.C
解:十二边形的内角和为,
故选C.
2.B
解:根据题意该多边形每个外角是,
,则这个多边形是六边形.
故选:B.
3.B
解:设这个多边形边数是n,根据题意得:
,
解得:,
即这个多边形是四边形,故B正确.
故选:B.
4.C
解:如图,连接并延长,
,,
,
、相邻的两外角平分线交于点,
,
,,
即
.
故选:.
5.B
解:如图,延长 ,交于点,
,
,
正多边形的一个外角为,
.
故选:B.
6.D
解:∵一个多边形的每一个外角都是,
∴这个多边形的边数为,
故选:D.
7.C
解:多边形的内角和可以表示成(且n是正整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,
根据题意得,
解得:,
则多边形的边数是或或,故C正确.
故选:C.
8.D
解:∵,,四边形内角和为360度,
∴,
故选:D.
9.B
解:如图,延长交于,
∵正五边形的内角和为,正六边形的内角和为,多边形的外角和为,
∴正六边形的一个内角和外角分别为、,正五边形的一个内角和外角分别为、,
∴,,,
在五边形中,,
∴,
在五边形中,,
故选:B.
10.D
解:∵奇奇从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为,
则一共走了米.
故选D.
11.D
解:过点E作,
∵、分别是和的平分线,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选D.
12.D
解:∵在正六边形和正方形中,
∴,,
∴,故A选项正确,不符合题意;
∵在正六边形和正方形中,
∴,,
∴,故B选项正确,不符合题意;
∵多边形是正六边形,
∴该多边形内角和为:,
∴,
∵多边形是正方形,
∴该多边形内角和为:,
∴,
∴,故C选项正确,不符合题意;
∵,
∴,故D选项不正确,符合题意
故选:D.
13.
解:设这个多边形边数为,
依题意,得:,
解得:,
∴这个多边形的边数是7.
故答案为:.
14.
解:n边形的内角和是,
边数增加2,则新的多边形的内角和是.
∵.
故它的内角和增加.
故答案为:.
15.6
解:设个多边形边数为n,三个钝角分别为,
∵,,,
∴,
∵该凸多边形恰好有三个内角是钝角,
∴凸多边形恰好有个锐角,
根据锐角的定义可得:所有的锐角和,
∴该多边形的内角和,
解得:,
∵n为整数,
∴n的最大值为6.
16.72
解:∵五边形为正五边形,
∴,,
∴,
∴.
故答案为:72.
17.
解:∵正五边形,
∴,
∵正方形,
∴,
∴,
∵,
∴.
故答案为:.
18.9
解:设这个多边形的边数为n,
由题意得:,
解得,
∴这个多边形的边数为9.
19.2条,3个,这几个三角形所有内角之和与五边形内角之和相等
解:五边形中,过顶点最多能引2条对角线,它们将五边形分为3个三角形,这几个三角形所有内角之和与五边形内角之和相等.
20.
解:五边形的内角和等于,,
;
,分别平分,,
,
;
故答案为:.
21.(1)这个多边形的边数是7
(2)14条
(1)解:设这个多边形的边数为n,
,
解得.
即这个多边形的边数是7.
(2)解:,
即这个多边形有14条对角线.
22.(1);;;;18;
(2)不存在,理由见解析
(1)解:填表如下:
正多边形的边数 3 4 5 6 18
的度数
故答案为:,,,,18;
(2)解:不存在,理由如下:
假设存在正 边形使得,得,
解得:,又是正整数,
所以不存在正边形使得.
23.(1)见解析;(2)见解析
证明:(1),,,,
,
四边形的内角和是,
,
四边形的外角和是;
(2)过点作交于点,过点作交延长线于点,
,,
,
平分,
,
,
,
,
为中点,
.
