19.1.2矩形的判定能力提升练习(含解析)华东师大版数学八年级下册
文档属性
| 名称 | 19.1.2矩形的判定能力提升练习(含解析)华东师大版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 17:46:50 | ||
图片预览


文档简介
矩形的判定
能力提升练习
一、单选题
1.下列说法中错误的是( )
A.一组邻边相等的矩形是正方形
B.一组邻边相等的平行四边形是菱形
C.一组对边相等且有一个角是直角的四边形是矩形
D.一组对边平行且相等的四边形是平行四边形
2.工人师傅检查一个门框是否为矩形,下列方法中正确的是( )
A.测量两条对角线是否相等 B.测量一组邻边是否相等
C.测量两条对角线是否互相垂直 D.测量门框的三个角是否都是直角
3.证明:有三个角是直角的四边形是矩形.
已知:如图,.
求证:四边形是矩形.嘉琪的证明过程如下:
证明:∵,
∴,,
∴,,
∴四边形是平行四边形(①).
∵,
∴四边形是矩形(②).
在证明过程中,依据①、②分别表示( )
在证明过程中,依据①、②分别表示( )
A.①表示两组对边分别平行的四边形是平行四边形;②表示对角线相等的平行四边形是矩形
B.①表示两组对边分别相等的四边形是平行四边形;②表示有一个角是直角的平行四边形是矩形
C.①表示两组对边分别平行的四边形是平行四边形;②表示有一个角是直角的平行四边形是矩形
D.①表示两组对边分别相等的四边形是平行四边形;②表示对角线相等的平行四边形是矩形
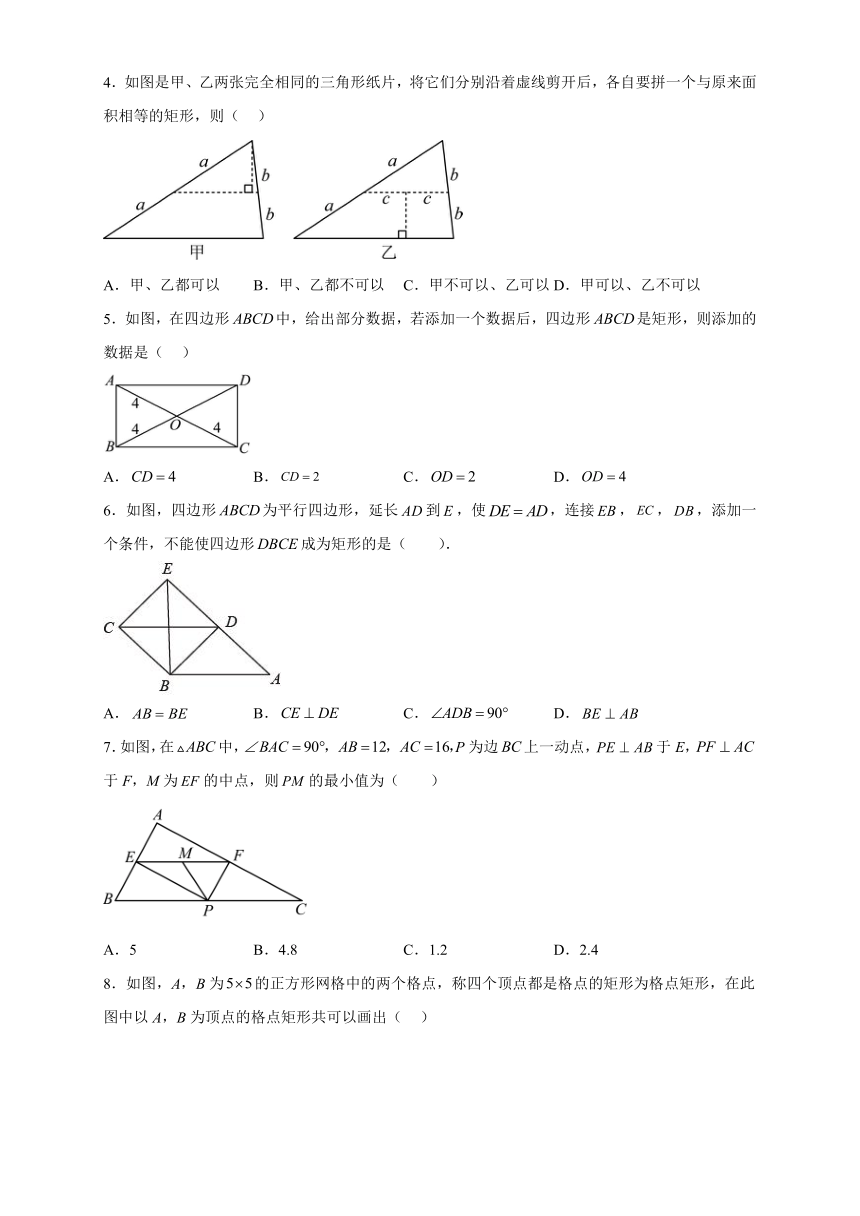
4.如图是甲、乙两张完全相同的三角形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的矩形,则( )
A.甲、乙都可以 B.甲、乙都不可以 C.甲不可以、乙可以 D.甲可以、乙不可以
5.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是( )
A. B. C. D.
6.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是( ).
A. B. C. D.
7.如图,在中,P为边上一动点,于E,于F,M为的中点,则的最小值为( )
A.5 B.4.8 C.1.2 D.2.4
8.如图,A,B为的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出( )
A.1个 B.2个 C.3个 D.4个
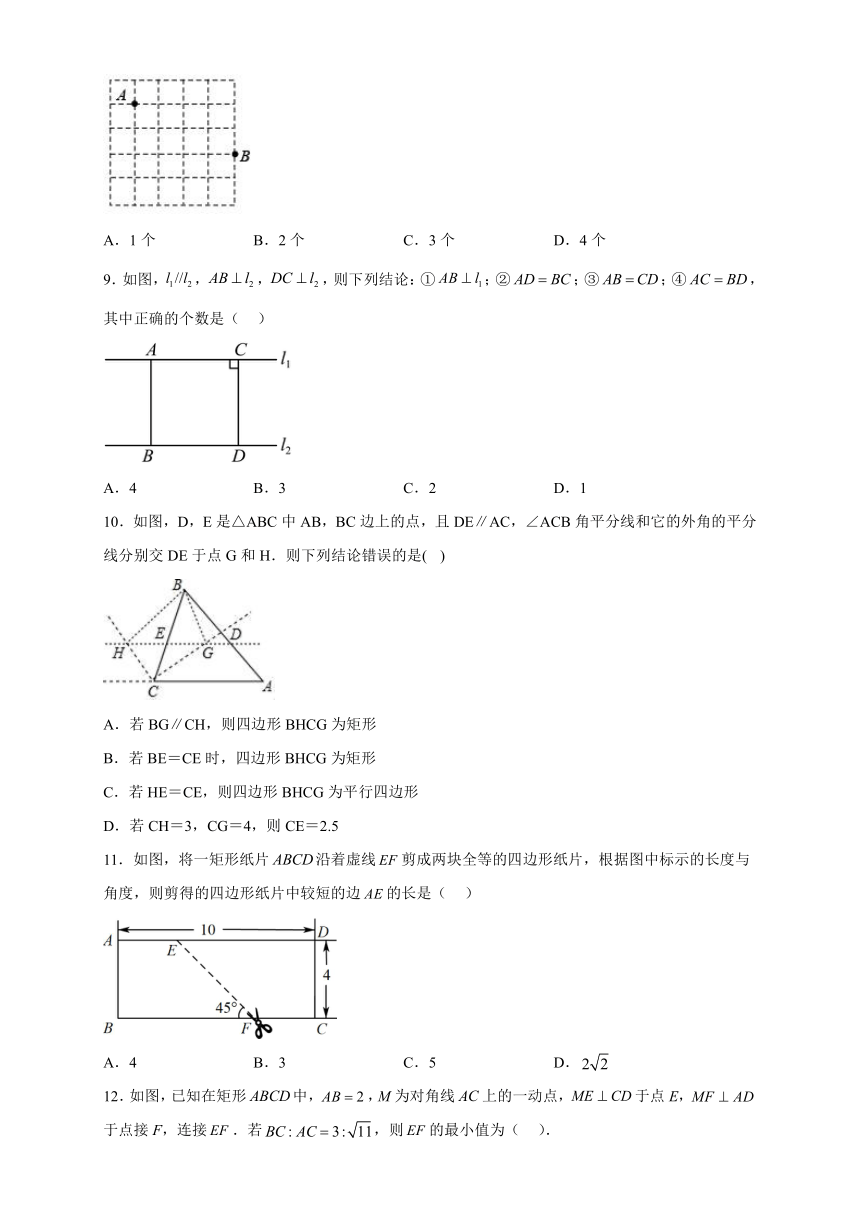
9.如图,,,,则下列结论:①;②;③;④,其中正确的个数是( )
A.4 B.3 C.2 D.1
10.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形
B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形
D.若CH=3,CG=4,则CE=2.5
11.如图,将一矩形纸片沿着虚线剪成两块全等的四边形纸片,根据图中标示的长度与角度,则剪得的四边形纸片中较短的边的长是( )
A.4 B.3 C.5 D.
12.如图,已知在矩形中,,M为对角线上的一动点,于点E,于点接F,连接.若,则的最小值为( ).
A. B. C. D.
13.如图,矩形在矩形的内部,且,点,在对角线的异侧.连结,,,,若矩形矩形,且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形的面积( )
A.矩形的面积 B.的度数
C.四边形的周长 D.的长度
二、填空题
14.如图,在平行四边形ABCD中,为边上一点,以为边作矩形.若,,则的大小为______度.
15.如图,点A在函数的图象上,过A作轴,与的图象交于点B,点C、D在x轴上,若,则四边形的面积为_______.
16.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为__________.
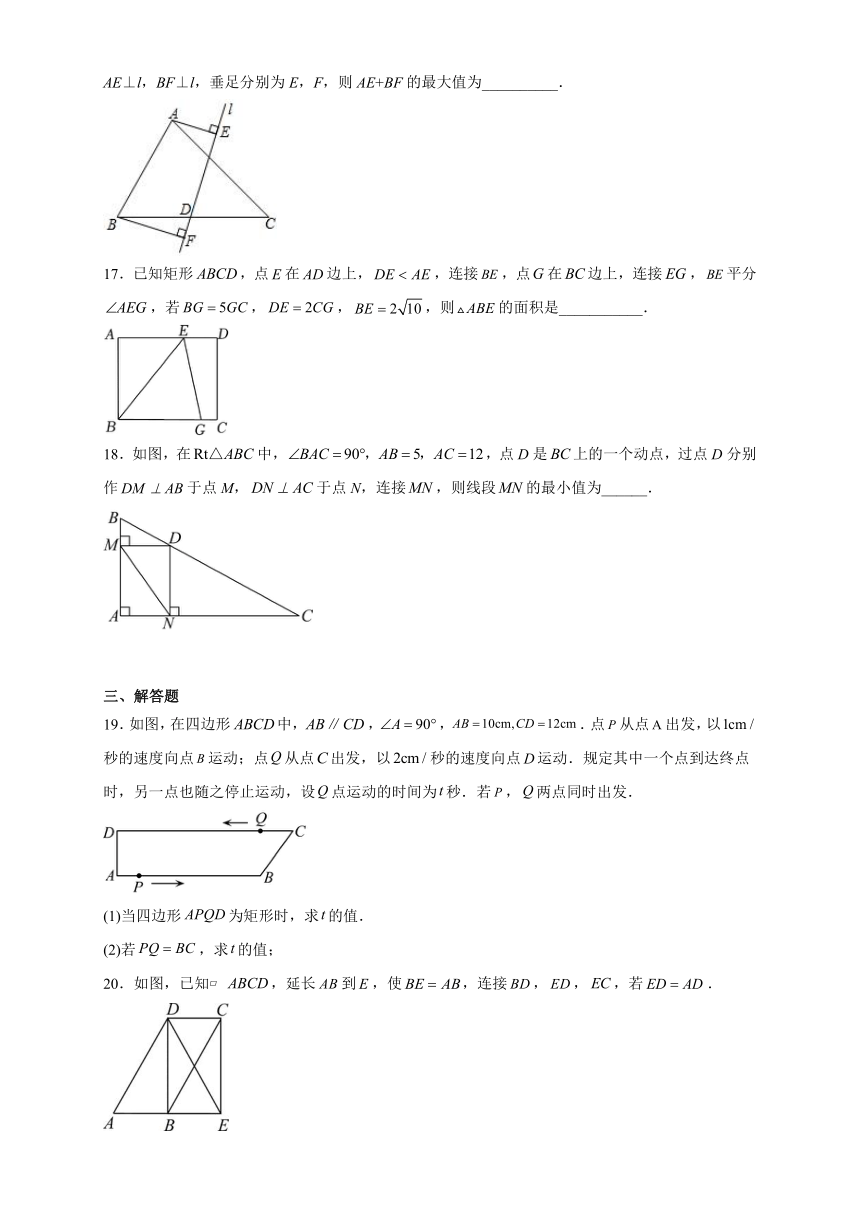
17.已知矩形,点在边上,,连接,点在边上,连接,平分,若,,,则的面积是___________.
18.如图,在中,,点D是上的一个动点,过点D分别作于点M,于点N,连接,则线段的最小值为______.
三、解答题
19.如图,在四边形中,,,.点从点出发,以秒的速度向点运动;点从点出发,以秒的速度向点运动.规定其中一个点到达终点时,另一点也随之停止运动,设点运动的时间为秒.若,两点同时出发.
(1)当四边形为矩形时,求的值.
(2)若,求的值;
20.如图,已知 ,延长到,使,连接,,,若.
(1)求证:;
(2)求证:四边形是矩形.
21.如图,四边形是平行四边形,过点D作于点E,点F在边上,,连接 ,
(1)求证:四边形是矩形
(2)若是的平分线.若,,求的长
22.如图,是的中线,,交于点F,且
(1)求证:;
(2)求证:四边形是平行四边形;
(3)当、之间满足什么条件时,四边形是矩形;
23.如图1,平行四边形ABCD中,连接,过点作于,点在上且,连接,过点作交的延长线于点.
(1)求证:四边形是矩形;
(2)如图2,连接、、,当时,在不添加辅助线和字母的情况下,直接写出图中的所有等腰三角形.
参考答案
1.C
解:根据正方形、菱形、平行四边形的定义知A、B、D正确;
一组对边相等且有一个角是直角的四边形不一定是矩形,选项C错误.
故选:C.
2.D
解:由对角线相等的四边形不一定是矩形,故A不符合题意;
由一组邻边相等的四边形不一定是矩形,故B不符合题意;
由两条对角线互相垂直的四边形不一定是矩形,故C不符合题意;
由三个角都是直角的四边形是矩形,故D符合题意.
故选D.
3.C
解:由,,推出四边形是平行四边形的依据是:两组对边分别平行的四边形是平行四边形;
由推出四边形是矩形的依据是:有一个角是直角的平行四边形是矩形,
故选:C.
4.A
解:所做图形如图所示:
甲乙够可以拼成一个与原来面积相等的矩形,
故选:A.
5.D
解:当时,由题意可知,
,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
故选:D
6.D
解:∵四边形ABCD是平行四边形
∴AB=CD,BC=AD,BC//AD,AB//CD
∵DE=AD
∴BC=DE
∵BC//AD
∴BC//DE
∴四边形DBCE是平行四边形
当AB=BE时,则由AB=CD得BE=CD,即四边形DBCE的两条对角线相等,根据矩形的判定知,四边形DBCE是矩形,故A不符合题意;
当CE⊥DE时或时,根据矩形的定义即知,四边形DBCE是矩形,故B、C不符合题意;
当时,则由AB//CD,可知BE⊥CD,即的对角线相互垂直,则四边形是菱形,但不能判定它是矩形,故D符合题意.
故选:D.
7.B
解:连接,如图所示:
∵,
∴,
∵,
∴四边形是矩形,
∴,与互相平分,
∵M是的中点,
∴M为的中点,
∴,
根据直线外一点到直线上任一点的距离,垂线段最短,
即时,最短,同样也最短,
∴当时,,
∴最短时,
∴当最短时,.
故选:B.
8.D
解:共可以画出以下4个格点矩形:
故选:D.
9.A
解:∵,,
∴AB∥CD,
∵,
∴四边形ABDC是平行四边形,
∵,
∴四边形ABDC是矩形,
∴∠BAC=90°,
∴,AD=BC,AB=CD,AC=BD,
故正确结论有4个,
故选:A.
10.C
解:∵∠ACB角平分线和它的外角的平分线分别交DE于点G和H,
∴∠HCG=90°,∠ECG=∠ACG;
∵DE∥AC.
∴∠ACG=∠HGC=∠ECG.
∴EC=EG;
同理:HE=EC,
∴HE=EC=EG=HG;
若CH∥BG,
∴∠HCG=∠BGC=90°,
∴∠EGB=∠EBG,
∴BE=EG,
∴BE=EG=HE=EC,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形;
故A正确;
若BE=CE,
∴BE=CE=HE=EG,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形,
故B正确;
若HE=EC,则不可以证明四边形BHCG为平行四边形,
故C错误;
若CH=3,CG=4,根据勾股定理可得HG=5,
∴CE=2.5,
故D正确.
故选C.
11.B
解:过F作FQ⊥AD于Q,则∠FQA=∠FQD=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,AB=DC=4,ADBC,
∴四边形ABFQ、四边形CDQF都是矩形,
∴AB=FQ=DC=4,QD=CF,
由题意得:AE=CF,
∴AE=QD,
∵ADBC,
∴∠QEF=∠BFE=45°,
∴△QEF是等腰直角三角形,
∴EQ=FQ=4,
∴AE=QD=×(10-4)=3,
故选:B.
12.D
解:如图,连接.
∵,
∴设,则,
∵四边形为矩形,
∴,,,
∴,即,
解得:(舍去负值),
∴,.
∵于点E,于点接F,
∴四边形为矩形,
∴,
∴当最小时,最小.
由垂线段最短可知:当时,最小,即此时为边上的高,
∵,
∴,即,
解得:.
∴最小值为.
故选D.
13.A
解:如图,连接,,过点作于点,过点作于点,过点作于点,过点作于点,
,
四边形、四边形是矩形,
设小矩形的长和宽分别为和,大矩形的长和宽分别为和,,,则,,,,
,,,,
,
矩形和矩形的周长已知,
和为定值,
为定值,
为定值,
,
当已知时,四边形的面积即为定值,
故选:A.
14.60
解:四边形是矩形,
,
,
,
,
四边形是平行四边形,
故答案为:60.
15.2
解:如图,延长交y轴于E,过A点作轴于M,作轴于N,
∴四边形、四边形、四边形均为矩形.
∵轴,,
∴四边形为平行四边形,
∴平行四边形的面积等于矩形的面积.
∵点A在反比例函数的图象上,点B在反比例函数的图象上,
∴,,
∴,
∴四边形的面积为2.
故答案为:2.
16.
解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,
在Rt△AHB中,
∵∠ABC=60°,AB=2,
∴BH=1,AH=,
在Rt△AHC中,∠ACB=45°,
∴△AHC是等腰直角三角形,AH=HC=,
∴AC=,
∵点D为BC中点,
∴BD=CD,
在△BFD与△CKD中,
,
∴△BFD≌△CKD(AAS),
∴BF=CK,
过点C作CN⊥AE交AE的延长线于点N,
∵∠CKE=∠KEN=∠ENC=90°,
∴四边形CKEN是矩形,
∴CK=EN=BF,
可得AE+BF=AE+CK=AE+EN=AN,
在Rt△ACN中,AN<AC,
当直线l⊥AC时,AN和AC重合,AN最大值为,
综上所述,AE+BF的最大值为.
故答案为:
17.
解:如图,过点作于,
设,则,,
平分,
,
,
,
,
,,
四边形是矩形,
,
,,
,,
,
(负值舍去),
,,,,
,,
,
,
故答案为:.
18.
解:如图所示,过点A作于H,连接,
在中,,
∴,
∵,
∴,
∵,,,
∴四边形是矩形,
∴,
∴当最小时,最小,
∴当与重合时,有最小值,
故答案为:.
19.(1)
(2)或
(1)解:∵ ,
∴,
由题意得,,
∴,
∵四边形APQD为矩形,
∴,
∴,
解得;
(2)解:如图2所示,作于点N,作于点H,则四边形为矩形,四边形为矩形,
∴,,,
又∵,
∴,
∴,
∴,
∴,
解得;
如图3所示,作于点E,作于点F,
同理可证,
∴,
∴,
∴,
解得;
综上所述,t的值为或.
20.(1)见解析
(2)见解析
(1)证明:,
,
,
;
(2)证明:,
,
,
,
,
,
21.(1)证明见解析;
(2)16
(1)证明:∵四边形是平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形;
(2)解:由(1)可知,四边形是矩形,
∴,
∴,
∵,,
∴,
∵四边形是平行四边形,
∴,,
∴,
∵是的平分线,
∴,
∴,
∴,
∴.
22.(1)证明见详解;
(2)证明见详解;
(3)时四边形是矩形,理由见详解;
(1)证明:∵,
∴,
在与中,
∴;
(2)证明:∵是的中线,
∴,
∵,
∴,
∴,
∵,
∴四边形是平行四边形;
(3)解:当时四边形是矩形,
∵,,
∴,
∵四边形是平行四边形,
∴四边形是矩形;
23.(1)证明见解析
(2),,,
解:(1)∵平行四边形ABCD中,
∴,,
∴.
又∵,
∴,
∴.
∵,
∴,
∴.
∵,
∴.
∵
∴四边形是矩形.
(2)∵四边形是矩形,
∴,
∴.
又∵,
∴,
∴四边形是平行四边形.
∴,
∴是等腰三角形,
∴,,
∴垂直平分,
∴,
∴是等腰三角形,
∴图中的等腰三角形有:,,,.
能力提升练习
一、单选题
1.下列说法中错误的是( )
A.一组邻边相等的矩形是正方形
B.一组邻边相等的平行四边形是菱形
C.一组对边相等且有一个角是直角的四边形是矩形
D.一组对边平行且相等的四边形是平行四边形
2.工人师傅检查一个门框是否为矩形,下列方法中正确的是( )
A.测量两条对角线是否相等 B.测量一组邻边是否相等
C.测量两条对角线是否互相垂直 D.测量门框的三个角是否都是直角
3.证明:有三个角是直角的四边形是矩形.
已知:如图,.
求证:四边形是矩形.嘉琪的证明过程如下:
证明:∵,
∴,,
∴,,
∴四边形是平行四边形(①).
∵,
∴四边形是矩形(②).
在证明过程中,依据①、②分别表示( )
在证明过程中,依据①、②分别表示( )
A.①表示两组对边分别平行的四边形是平行四边形;②表示对角线相等的平行四边形是矩形
B.①表示两组对边分别相等的四边形是平行四边形;②表示有一个角是直角的平行四边形是矩形
C.①表示两组对边分别平行的四边形是平行四边形;②表示有一个角是直角的平行四边形是矩形
D.①表示两组对边分别相等的四边形是平行四边形;②表示对角线相等的平行四边形是矩形
4.如图是甲、乙两张完全相同的三角形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的矩形,则( )
A.甲、乙都可以 B.甲、乙都不可以 C.甲不可以、乙可以 D.甲可以、乙不可以
5.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是( )
A. B. C. D.
6.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是( ).
A. B. C. D.
7.如图,在中,P为边上一动点,于E,于F,M为的中点,则的最小值为( )
A.5 B.4.8 C.1.2 D.2.4
8.如图,A,B为的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出( )
A.1个 B.2个 C.3个 D.4个
9.如图,,,,则下列结论:①;②;③;④,其中正确的个数是( )
A.4 B.3 C.2 D.1
10.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形
B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形
D.若CH=3,CG=4,则CE=2.5
11.如图,将一矩形纸片沿着虚线剪成两块全等的四边形纸片,根据图中标示的长度与角度,则剪得的四边形纸片中较短的边的长是( )
A.4 B.3 C.5 D.
12.如图,已知在矩形中,,M为对角线上的一动点,于点E,于点接F,连接.若,则的最小值为( ).
A. B. C. D.
13.如图,矩形在矩形的内部,且,点,在对角线的异侧.连结,,,,若矩形矩形,且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形的面积( )
A.矩形的面积 B.的度数
C.四边形的周长 D.的长度
二、填空题
14.如图,在平行四边形ABCD中,为边上一点,以为边作矩形.若,,则的大小为______度.
15.如图,点A在函数的图象上,过A作轴,与的图象交于点B,点C、D在x轴上,若,则四边形的面积为_______.
16.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为__________.
17.已知矩形,点在边上,,连接,点在边上,连接,平分,若,,,则的面积是___________.
18.如图,在中,,点D是上的一个动点,过点D分别作于点M,于点N,连接,则线段的最小值为______.
三、解答题
19.如图,在四边形中,,,.点从点出发,以秒的速度向点运动;点从点出发,以秒的速度向点运动.规定其中一个点到达终点时,另一点也随之停止运动,设点运动的时间为秒.若,两点同时出发.
(1)当四边形为矩形时,求的值.
(2)若,求的值;
20.如图,已知 ,延长到,使,连接,,,若.
(1)求证:;
(2)求证:四边形是矩形.
21.如图,四边形是平行四边形,过点D作于点E,点F在边上,,连接 ,
(1)求证:四边形是矩形
(2)若是的平分线.若,,求的长
22.如图,是的中线,,交于点F,且
(1)求证:;
(2)求证:四边形是平行四边形;
(3)当、之间满足什么条件时,四边形是矩形;
23.如图1,平行四边形ABCD中,连接,过点作于,点在上且,连接,过点作交的延长线于点.
(1)求证:四边形是矩形;
(2)如图2,连接、、,当时,在不添加辅助线和字母的情况下,直接写出图中的所有等腰三角形.
参考答案
1.C
解:根据正方形、菱形、平行四边形的定义知A、B、D正确;
一组对边相等且有一个角是直角的四边形不一定是矩形,选项C错误.
故选:C.
2.D
解:由对角线相等的四边形不一定是矩形,故A不符合题意;
由一组邻边相等的四边形不一定是矩形,故B不符合题意;
由两条对角线互相垂直的四边形不一定是矩形,故C不符合题意;
由三个角都是直角的四边形是矩形,故D符合题意.
故选D.
3.C
解:由,,推出四边形是平行四边形的依据是:两组对边分别平行的四边形是平行四边形;
由推出四边形是矩形的依据是:有一个角是直角的平行四边形是矩形,
故选:C.
4.A
解:所做图形如图所示:
甲乙够可以拼成一个与原来面积相等的矩形,
故选:A.
5.D
解:当时,由题意可知,
,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
故选:D
6.D
解:∵四边形ABCD是平行四边形
∴AB=CD,BC=AD,BC//AD,AB//CD
∵DE=AD
∴BC=DE
∵BC//AD
∴BC//DE
∴四边形DBCE是平行四边形
当AB=BE时,则由AB=CD得BE=CD,即四边形DBCE的两条对角线相等,根据矩形的判定知,四边形DBCE是矩形,故A不符合题意;
当CE⊥DE时或时,根据矩形的定义即知,四边形DBCE是矩形,故B、C不符合题意;
当时,则由AB//CD,可知BE⊥CD,即的对角线相互垂直,则四边形是菱形,但不能判定它是矩形,故D符合题意.
故选:D.
7.B
解:连接,如图所示:
∵,
∴,
∵,
∴四边形是矩形,
∴,与互相平分,
∵M是的中点,
∴M为的中点,
∴,
根据直线外一点到直线上任一点的距离,垂线段最短,
即时,最短,同样也最短,
∴当时,,
∴最短时,
∴当最短时,.
故选:B.
8.D
解:共可以画出以下4个格点矩形:
故选:D.
9.A
解:∵,,
∴AB∥CD,
∵,
∴四边形ABDC是平行四边形,
∵,
∴四边形ABDC是矩形,
∴∠BAC=90°,
∴,AD=BC,AB=CD,AC=BD,
故正确结论有4个,
故选:A.
10.C
解:∵∠ACB角平分线和它的外角的平分线分别交DE于点G和H,
∴∠HCG=90°,∠ECG=∠ACG;
∵DE∥AC.
∴∠ACG=∠HGC=∠ECG.
∴EC=EG;
同理:HE=EC,
∴HE=EC=EG=HG;
若CH∥BG,
∴∠HCG=∠BGC=90°,
∴∠EGB=∠EBG,
∴BE=EG,
∴BE=EG=HE=EC,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形;
故A正确;
若BE=CE,
∴BE=CE=HE=EG,
∴CHBG是平行四边形,且∠HCG=90°,
∴CHBG是矩形,
故B正确;
若HE=EC,则不可以证明四边形BHCG为平行四边形,
故C错误;
若CH=3,CG=4,根据勾股定理可得HG=5,
∴CE=2.5,
故D正确.
故选C.
11.B
解:过F作FQ⊥AD于Q,则∠FQA=∠FQD=90°,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,AB=DC=4,ADBC,
∴四边形ABFQ、四边形CDQF都是矩形,
∴AB=FQ=DC=4,QD=CF,
由题意得:AE=CF,
∴AE=QD,
∵ADBC,
∴∠QEF=∠BFE=45°,
∴△QEF是等腰直角三角形,
∴EQ=FQ=4,
∴AE=QD=×(10-4)=3,
故选:B.
12.D
解:如图,连接.
∵,
∴设,则,
∵四边形为矩形,
∴,,,
∴,即,
解得:(舍去负值),
∴,.
∵于点E,于点接F,
∴四边形为矩形,
∴,
∴当最小时,最小.
由垂线段最短可知:当时,最小,即此时为边上的高,
∵,
∴,即,
解得:.
∴最小值为.
故选D.
13.A
解:如图,连接,,过点作于点,过点作于点,过点作于点,过点作于点,
,
四边形、四边形是矩形,
设小矩形的长和宽分别为和,大矩形的长和宽分别为和,,,则,,,,
,,,,
,
矩形和矩形的周长已知,
和为定值,
为定值,
为定值,
,
当已知时,四边形的面积即为定值,
故选:A.
14.60
解:四边形是矩形,
,
,
,
,
四边形是平行四边形,
故答案为:60.
15.2
解:如图,延长交y轴于E,过A点作轴于M,作轴于N,
∴四边形、四边形、四边形均为矩形.
∵轴,,
∴四边形为平行四边形,
∴平行四边形的面积等于矩形的面积.
∵点A在反比例函数的图象上,点B在反比例函数的图象上,
∴,,
∴,
∴四边形的面积为2.
故答案为:2.
16.
解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,
在Rt△AHB中,
∵∠ABC=60°,AB=2,
∴BH=1,AH=,
在Rt△AHC中,∠ACB=45°,
∴△AHC是等腰直角三角形,AH=HC=,
∴AC=,
∵点D为BC中点,
∴BD=CD,
在△BFD与△CKD中,
,
∴△BFD≌△CKD(AAS),
∴BF=CK,
过点C作CN⊥AE交AE的延长线于点N,
∵∠CKE=∠KEN=∠ENC=90°,
∴四边形CKEN是矩形,
∴CK=EN=BF,
可得AE+BF=AE+CK=AE+EN=AN,
在Rt△ACN中,AN<AC,
当直线l⊥AC时,AN和AC重合,AN最大值为,
综上所述,AE+BF的最大值为.
故答案为:
17.
解:如图,过点作于,
设,则,,
平分,
,
,
,
,
,,
四边形是矩形,
,
,,
,,
,
(负值舍去),
,,,,
,,
,
,
故答案为:.
18.
解:如图所示,过点A作于H,连接,
在中,,
∴,
∵,
∴,
∵,,,
∴四边形是矩形,
∴,
∴当最小时,最小,
∴当与重合时,有最小值,
故答案为:.
19.(1)
(2)或
(1)解:∵ ,
∴,
由题意得,,
∴,
∵四边形APQD为矩形,
∴,
∴,
解得;
(2)解:如图2所示,作于点N,作于点H,则四边形为矩形,四边形为矩形,
∴,,,
又∵,
∴,
∴,
∴,
∴,
解得;
如图3所示,作于点E,作于点F,
同理可证,
∴,
∴,
∴,
解得;
综上所述,t的值为或.
20.(1)见解析
(2)见解析
(1)证明:,
,
,
;
(2)证明:,
,
,
,
,
,
21.(1)证明见解析;
(2)16
(1)证明:∵四边形是平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形;
(2)解:由(1)可知,四边形是矩形,
∴,
∴,
∵,,
∴,
∵四边形是平行四边形,
∴,,
∴,
∵是的平分线,
∴,
∴,
∴,
∴.
22.(1)证明见详解;
(2)证明见详解;
(3)时四边形是矩形,理由见详解;
(1)证明:∵,
∴,
在与中,
∴;
(2)证明:∵是的中线,
∴,
∵,
∴,
∴,
∵,
∴四边形是平行四边形;
(3)解:当时四边形是矩形,
∵,,
∴,
∵四边形是平行四边形,
∴四边形是矩形;
23.(1)证明见解析
(2),,,
解:(1)∵平行四边形ABCD中,
∴,,
∴.
又∵,
∴,
∴.
∵,
∴,
∴.
∵,
∴.
∵
∴四边形是矩形.
(2)∵四边形是矩形,
∴,
∴.
又∵,
∴,
∴四边形是平行四边形.
∴,
∴是等腰三角形,
∴,,
∴垂直平分,
∴,
∴是等腰三角形,
∴图中的等腰三角形有:,,,.
