华师大版数学七年级上册 5.1 第2课时 垂线 课件(共19张PPT)
文档属性
| 名称 | 华师大版数学七年级上册 5.1 第2课时 垂线 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 692.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 18:45:29 | ||
图片预览




文档简介
(共19张PPT)
5.1 相交线
第2课时 垂线
1.在现实情境中,通过画、折等活动,进一步丰富对两条直线互相垂直的认识,掌握有关的符号表示.
3. 掌握有关垂直的一些性质.
2.会借助三角尺、量角器、方格纸画垂线,进一步丰富操作活动的经验.
学习目标
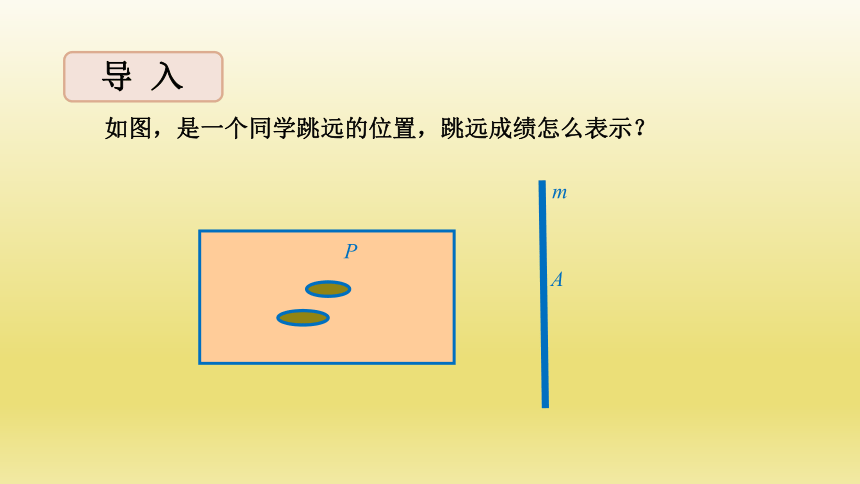
如图,是一个同学跳远的位置,跳远成绩怎么表示?
m
P
A
导 入
平面内的两条直线有哪些位置关系
平行
相交
温故知新
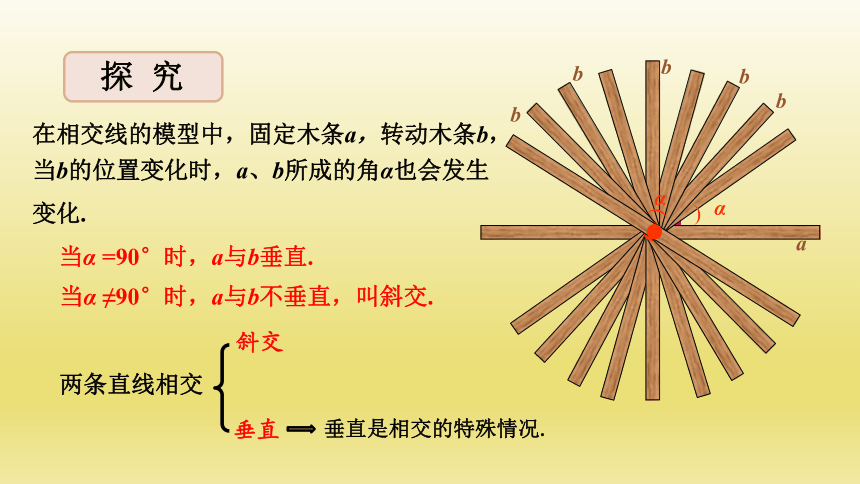
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况.
)
α
a
b
b
b
b
b
)
α
探 究
O
B
A
C
D
当两条直线AB,CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直,记作“AB⊥CD”,它们的交点O叫做垂足.我们把其中一条直线叫做另一条直线的垂线.
新知讲解
你能举例说明生活中有哪些垂直的现象吗?
思 考
你能举例说明生活中有哪些垂直的现象吗?
思 考
1.你能用三角尺在白纸上画两条互相垂直的直线吗?
3.如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
2.你能用量角器在白纸上画两条互相垂直的直线吗?
思 考
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
用三角尺作两条互相垂直的直线.
思 考
O
D
C
B
A
m
n
图中,直线AB与直线CD垂直,
记作:
AB⊥CD;
直线 m 与直线 n 垂直,
记作:m⊥n ;
互相垂直的两条直线的交点叫做垂足.
注意:
“⊥”是“垂直”的记号,
而“ ”是图形中“垂直(直角)” 的标记.
新知讲解
垂直的表示
在图中过点A作m的垂线,你能作多少条?
·
A
·
A
m
m
过一点有且只有一条直线与已知直线垂直.
思 考
看图回答:
你能用一句话表示这个结论吗?
P
A
B
C
m
D
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
直线外一点与直线上各点连成的所有线段中,垂线段最短.
线段PA,PB,PC,PD谁最短?
线段PB叫做点P到直线m的垂线段.
点到直线的距离
探 究
【例】作一条直线l,在直线l上取一点A,在l外取一点B,试分别过点A,B用三角尺作直线的垂线.
l
A
B
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
例 题
1.如图,∠BAC=90°,AD⊥BC于点D,则下面结论中正确的有( )
①点B到AC的垂线段是线段AB;
②线段AC是点C到AB的垂线段;
③线段AD是点A到BC的垂线段;
④线段BD是点B到AD的垂线段.
A.1个 B.2个 C.3个 D.4个
D
练 习
2.在数学课上,同学们在练习过点B作线段AC所在直线的垂线,有一部分学生画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
C
练 习
3.如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为_____________.
解析:虽然线段AD在五条线段中,长度是最短的,但是,题意没有说明线段AD 是线段BF 的垂线段,因此,无法断定线段AD的长是点A到BF的距离.
练 习
错误
4.如图,点O在直线AB上,OC平分∠BOD,OE平分∠AOD,则OE和OC有何位置关系?请简述你的理由.
解: OE和OC互相垂直.因为∠DOE等于∠AOD的一半, ∠COD等于∠DOB的一半,所以∠EOC等于180°的一半,即90°.
练 习
1.垂直的定义:
2.垂直的画法.
3.垂直的记法:
4.垂直的基本事实:
5.点到直线的距离:
总 结
当两条直线AB,CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直.
直线AB,CD互相垂直,记作“AB⊥CD”.
过一点有且只有一条直线与已知直线垂直.
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
5.1 相交线
第2课时 垂线
1.在现实情境中,通过画、折等活动,进一步丰富对两条直线互相垂直的认识,掌握有关的符号表示.
3. 掌握有关垂直的一些性质.
2.会借助三角尺、量角器、方格纸画垂线,进一步丰富操作活动的经验.
学习目标
如图,是一个同学跳远的位置,跳远成绩怎么表示?
m
P
A
导 入
平面内的两条直线有哪些位置关系
平行
相交
温故知新
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况.
)
α
a
b
b
b
b
b
)
α
探 究
O
B
A
C
D
当两条直线AB,CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直,记作“AB⊥CD”,它们的交点O叫做垂足.我们把其中一条直线叫做另一条直线的垂线.
新知讲解
你能举例说明生活中有哪些垂直的现象吗?
思 考
你能举例说明生活中有哪些垂直的现象吗?
思 考
1.你能用三角尺在白纸上画两条互相垂直的直线吗?
3.如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
2.你能用量角器在白纸上画两条互相垂直的直线吗?
思 考
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
用三角尺作两条互相垂直的直线.
思 考
O
D
C
B
A
m
n
图中,直线AB与直线CD垂直,
记作:
AB⊥CD;
直线 m 与直线 n 垂直,
记作:m⊥n ;
互相垂直的两条直线的交点叫做垂足.
注意:
“⊥”是“垂直”的记号,
而“ ”是图形中“垂直(直角)” 的标记.
新知讲解
垂直的表示
在图中过点A作m的垂线,你能作多少条?
·
A
·
A
m
m
过一点有且只有一条直线与已知直线垂直.
思 考
看图回答:
你能用一句话表示这个结论吗?
P
A
B
C
m
D
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
直线外一点与直线上各点连成的所有线段中,垂线段最短.
线段PA,PB,PC,PD谁最短?
线段PB叫做点P到直线m的垂线段.
点到直线的距离
探 究
【例】作一条直线l,在直线l上取一点A,在l外取一点B,试分别过点A,B用三角尺作直线的垂线.
l
A
B
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
例 题
1.如图,∠BAC=90°,AD⊥BC于点D,则下面结论中正确的有( )
①点B到AC的垂线段是线段AB;
②线段AC是点C到AB的垂线段;
③线段AD是点A到BC的垂线段;
④线段BD是点B到AD的垂线段.
A.1个 B.2个 C.3个 D.4个
D
练 习
2.在数学课上,同学们在练习过点B作线段AC所在直线的垂线,有一部分学生画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
C
练 习
3.如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为_____________.
解析:虽然线段AD在五条线段中,长度是最短的,但是,题意没有说明线段AD 是线段BF 的垂线段,因此,无法断定线段AD的长是点A到BF的距离.
练 习
错误
4.如图,点O在直线AB上,OC平分∠BOD,OE平分∠AOD,则OE和OC有何位置关系?请简述你的理由.
解: OE和OC互相垂直.因为∠DOE等于∠AOD的一半, ∠COD等于∠DOB的一半,所以∠EOC等于180°的一半,即90°.
练 习
1.垂直的定义:
2.垂直的画法.
3.垂直的记法:
4.垂直的基本事实:
5.点到直线的距离:
总 结
当两条直线AB,CD所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,直线AB,CD互相垂直.
直线AB,CD互相垂直,记作“AB⊥CD”.
过一点有且只有一条直线与已知直线垂直.
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
