人教版数学七年级下册 7.2.2用坐标表示平移 课件(共18张PPT)
文档属性
| 名称 | 人教版数学七年级下册 7.2.2用坐标表示平移 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 799.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第 七章 平面直角坐标系
数学七年级下册 RJ
7.2 坐标方法的简单应用
7.2.2 用坐标表示平移
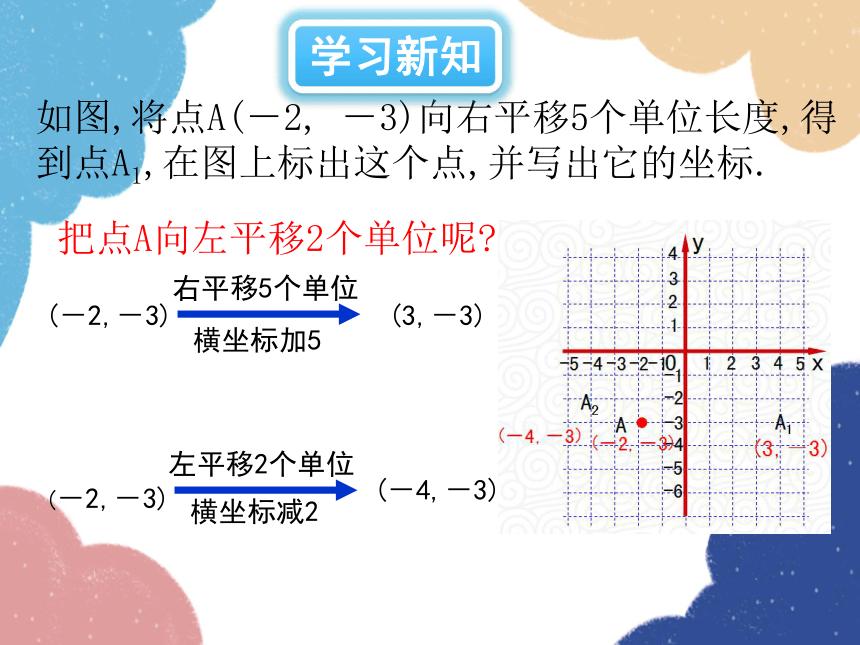
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢
(-2,-3)
右平移5个单位
(3,-3)
横坐标加5
(-2,-3)
左平移2个单位
(-4,-3)
横坐标减2
学习新知
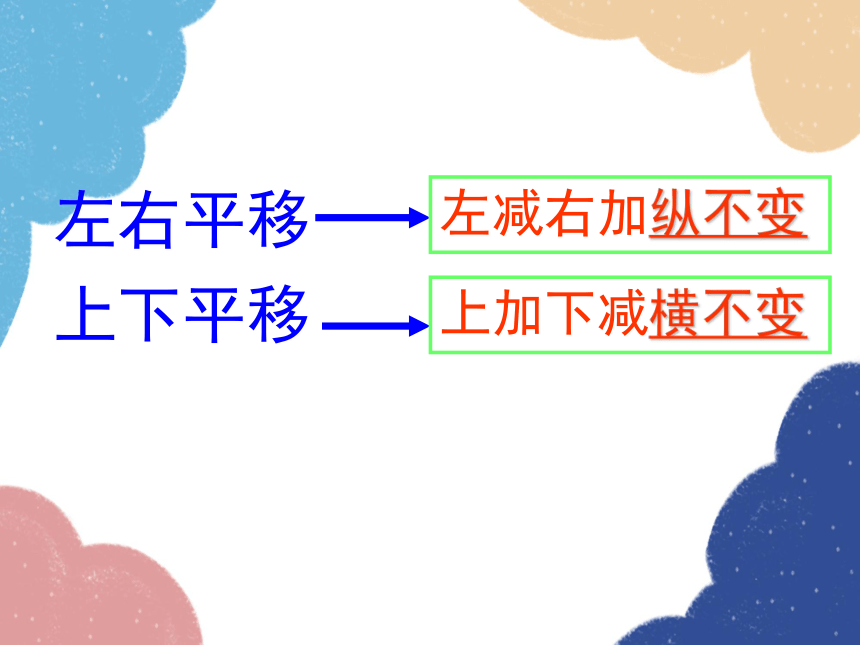
上下平移
左右平移
上加下减横不变
左减右加纵不变
1.将点A(3,2)向上平移2个单位长度,
得到A’,则A’的坐标为______.
2.将点A(3,2)向下平移3个单位长度,
得到A’,则A’的坐标为______.
3.将点A(3,2)向左平移4个单位长度,
得到A’,则A’的坐标为______.
4.将点A(3,2)向右平移2个单位长度,
得到A’,则A’的坐标为______.
(3,4)
(3,-1)
(-1,2)
(5,2)
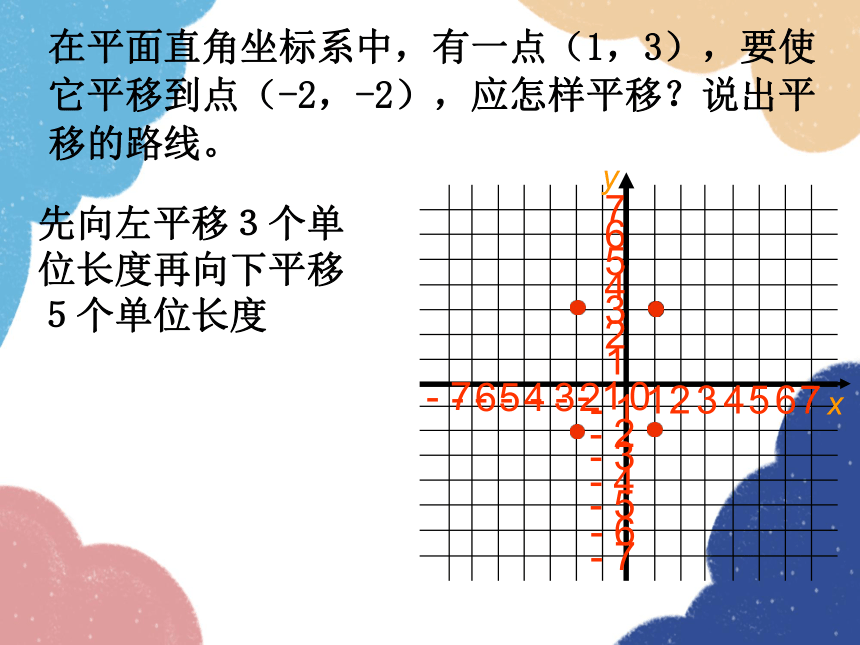
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线。
先向左平移3个单位长度再向下平移5个单位长度
- 5
- 4
- 3
- 2
- 7
- 6
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
x
y
- 5
- 4
- 3
- 2
- 7
- 6
- 1
- 1
1.把点M(1,2)平移后得到点N(1,-2)
则平移的过程是:
向下平移4个单位 .
2.把点M(-3,1)平移后得到点N(-1,4)
则平移的过程是:
向右平移2个单位,再向上平移3个单位
(或:向上平移3个单位,再向右平移2个单位) .
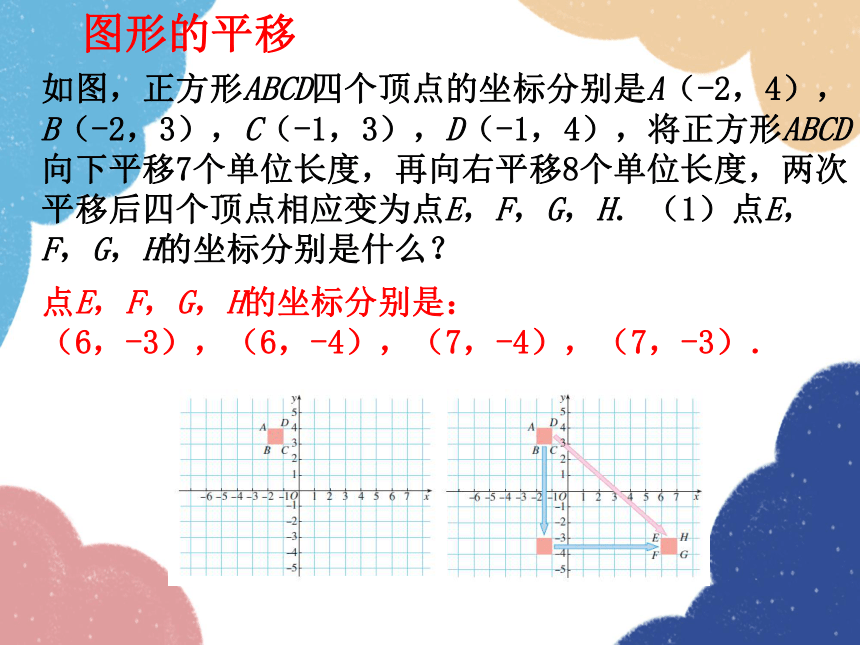
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.(1)点E,
F,G,H的坐标分别是什么?
点E,F,G,H的坐标分别是:
(6,-3),(6,-4),(7,-4),(7,-3).
图形的平移
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
若直接平移正方形ABCD,使点A移到点E,它就和我们前面得到的正方形位置相同.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图示上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
图形的平移
10
A
B
C
A’
C’
B’
C”
B”
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
A”
(-2,3)
(-3,1)
(-5,2)
(4,-2)
(3,-4)
(1,-3)
在此平移中对应点的坐标有何关系
(4,3)
(3,1)
(1,2)
(2)若将三角形ABC向下平移5个单位,请画出平移后的三角形,并写出A、B、C对应顶点的坐标.
(1)若将三角形ABC向左平移6个单位,请画出平移后的三角形,并写出A、B、C的对应点的坐标;
例1 如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移.
例2 如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)若将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接得到三角形A1B1C1 ,它与原三角形ABC的大小、位置有什么关系
解:三角形ABC的大小、形状完全相同,三角形A1B1C1可以看作将三角形ABC向左平移6个单位得到.
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移.
(2)若将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接得到三角形A2B2C2,它与原三角形ABC的大小、位置有什么关系
解:三角形ABC大小、形状完全相同,三角形A2B2C2可以看作将三角形ABC向下平移5个单位得到.
(1)横坐标变化,纵坐标不变
原图形向右平移a个单位
原图形上的点(x,y)
(x+a,y)
图形上点的坐标变化与图形平移间的关系
原图形向左平移a个单位
原图形上的点(x,y)
(x-a,y)
原图形向上平移b个单位
原图形上的点(x,y)
(x,y+b)
原图形向下平移b个单位
原图形上的点(x,y)
(x,y-b)
(2)横坐标不变,纵坐标变化
(a>0)
(b>0)
(3)上、下、左、右平移:
向右平移a个单位
原图形上的点(x,y) ,
向左平移a个单位
x+a, y+b
x-a, y+b
向上平移b个单位( )
原图形上的点(x,y) ,
向上平移b个单位( )
总结规律
图形上点的坐标变化与图形平移间的关系
在平面直角坐标系内,如果把一个图形各个
点的横坐标都加(或减去)一个正数a,相应的
新图形就是把原图形向 (或向 )平移 个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或 )平移__个单位长度.
右
左
上
下
a
a
【解析】选B.点C(3,3)向下平移5个单位,再向左平移2个单位,得到(1,-2).
已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
(A)(5,-2)(B)(1,-2)
(C)(2,-1)(D)(2,-2)
A
B
C
O
x
y
课堂检测
B
点(x,y)
向右平移a
(x+a,y)
向左平移a
(x-a,y)
向
上
平
移
a
(x,y+a)
向
下
平
移
a
(x,y-a)
左右平移
左减右加纵不变
课堂小结
在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或 )平移__个单位长度.
右
左
上
下
a
a
第 七章 平面直角坐标系
数学七年级下册 RJ
7.2 坐标方法的简单应用
7.2.2 用坐标表示平移
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢
(-2,-3)
右平移5个单位
(3,-3)
横坐标加5
(-2,-3)
左平移2个单位
(-4,-3)
横坐标减2
学习新知
上下平移
左右平移
上加下减横不变
左减右加纵不变
1.将点A(3,2)向上平移2个单位长度,
得到A’,则A’的坐标为______.
2.将点A(3,2)向下平移3个单位长度,
得到A’,则A’的坐标为______.
3.将点A(3,2)向左平移4个单位长度,
得到A’,则A’的坐标为______.
4.将点A(3,2)向右平移2个单位长度,
得到A’,则A’的坐标为______.
(3,4)
(3,-1)
(-1,2)
(5,2)
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线。
先向左平移3个单位长度再向下平移5个单位长度
- 5
- 4
- 3
- 2
- 7
- 6
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
x
y
- 5
- 4
- 3
- 2
- 7
- 6
- 1
- 1
1.把点M(1,2)平移后得到点N(1,-2)
则平移的过程是:
向下平移4个单位 .
2.把点M(-3,1)平移后得到点N(-1,4)
则平移的过程是:
向右平移2个单位,再向上平移3个单位
(或:向上平移3个单位,再向右平移2个单位) .
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.(1)点E,
F,G,H的坐标分别是什么?
点E,F,G,H的坐标分别是:
(6,-3),(6,-4),(7,-4),(7,-3).
图形的平移
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
若直接平移正方形ABCD,使点A移到点E,它就和我们前面得到的正方形位置相同.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图示上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
图形的平移
10
A
B
C
A’
C’
B’
C”
B”
x
y
O
1
2
3
4
2
4
1
3
5
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
A”
(-2,3)
(-3,1)
(-5,2)
(4,-2)
(3,-4)
(1,-3)
在此平移中对应点的坐标有何关系
(4,3)
(3,1)
(1,2)
(2)若将三角形ABC向下平移5个单位,请画出平移后的三角形,并写出A、B、C对应顶点的坐标.
(1)若将三角形ABC向左平移6个单位,请画出平移后的三角形,并写出A、B、C的对应点的坐标;
例1 如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移.
例2 如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)若将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接得到三角形A1B1C1 ,它与原三角形ABC的大小、位置有什么关系
解:三角形ABC的大小、形状完全相同,三角形A1B1C1可以看作将三角形ABC向左平移6个单位得到.
反过来,从图形上所有的点的坐标的某种变化;我们也可以看出对这个图形进行了怎样的平移.
(2)若将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接得到三角形A2B2C2,它与原三角形ABC的大小、位置有什么关系
解:三角形ABC大小、形状完全相同,三角形A2B2C2可以看作将三角形ABC向下平移5个单位得到.
(1)横坐标变化,纵坐标不变
原图形向右平移a个单位
原图形上的点(x,y)
(x+a,y)
图形上点的坐标变化与图形平移间的关系
原图形向左平移a个单位
原图形上的点(x,y)
(x-a,y)
原图形向上平移b个单位
原图形上的点(x,y)
(x,y+b)
原图形向下平移b个单位
原图形上的点(x,y)
(x,y-b)
(2)横坐标不变,纵坐标变化
(a>0)
(b>0)
(3)上、下、左、右平移:
向右平移a个单位
原图形上的点(x,y) ,
向左平移a个单位
x+a, y+b
x-a, y+b
向上平移b个单位( )
原图形上的点(x,y) ,
向上平移b个单位( )
总结规律
图形上点的坐标变化与图形平移间的关系
在平面直角坐标系内,如果把一个图形各个
点的横坐标都加(或减去)一个正数a,相应的
新图形就是把原图形向 (或向 )平移 个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或 )平移__个单位长度.
右
左
上
下
a
a
【解析】选B.点C(3,3)向下平移5个单位,再向左平移2个单位,得到(1,-2).
已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
(A)(5,-2)(B)(1,-2)
(C)(2,-1)(D)(2,-2)
A
B
C
O
x
y
课堂检测
B
点(x,y)
向右平移a
(x+a,y)
向左平移a
(x-a,y)
向
上
平
移
a
(x,y+a)
向
下
平
移
a
(x,y-a)
左右平移
左减右加纵不变
课堂小结
在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或 )平移__个单位长度.
右
左
上
下
a
a
