13.2.1 作轴对称图形 课件(共17张PPT)
文档属性
| 名称 | 13.2.1 作轴对称图形 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
画轴对称图形
课前回顾
轴对称图形的做法:
1、几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形.
2、对于一些由直线、线段或射线组成的图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形。
学习目标
学习目标
1.能知道关于x轴或关于y轴对称的点的坐标特征。
2. 能利用对称点坐标规律在平面直角坐标系中作出一个图形关于x、y轴的轴对称图形。
重点
掌握关于坐标轴对称的点的坐标规律。
难点
在平面直角坐标系中作出一个图形关于x、y轴的轴对称图形。
观察与思考
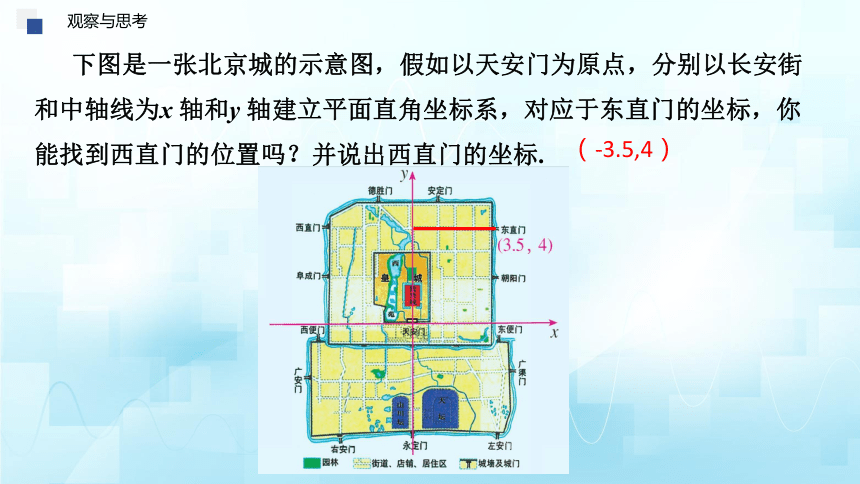
下图是一张北京城的示意图,假如以天安门为原点,分别以长安街和中轴线为x 轴和y 轴建立平面直角坐标系,对应于东直门的坐标,你能找到西直门的位置吗?并说出西直门的坐标.
(-3.5,4)
观察与思考
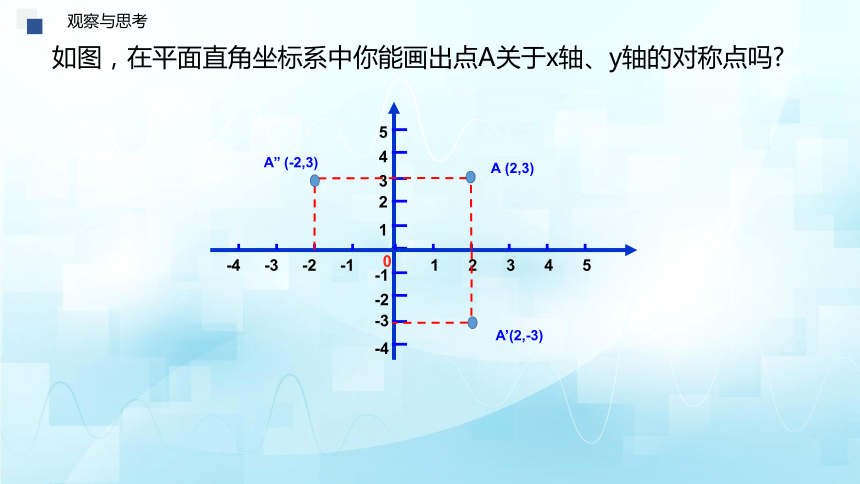
如图,在平面直角坐标系中你能画出点A关于x轴、y轴的对称点吗
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
A’(2,-3)
A’’ (-2,3)
观察与思考
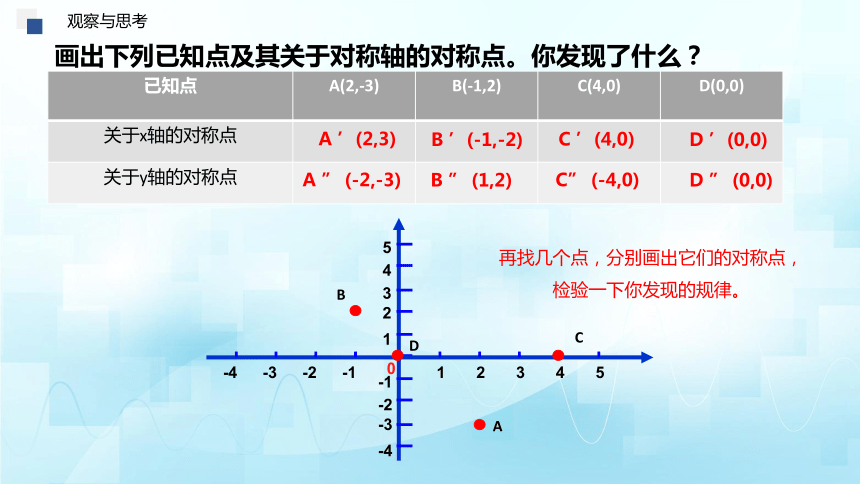
画出下列已知点及其关于对称轴的对称点。你发现了什么?
已知点 A(2,-3) B(-1,2) C(4,0) D(0,0)
关于x轴的对称点
关于y轴的对称点
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A ’(2,3)
A ” (-2,-3)
B ’(-1,-2)
B ” (1,2)
C ’(4,0)
C” (-4,0)
D ’(0,0)
D ” (0,0)
A
B
C
D
再找几个点,分别画出它们的对称点,检验一下你发现的规律。
小结
1.关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数. (简称:横轴横相等)
2.关于y轴对称的点的坐标的特点是:
纵坐标相等,横坐标互为相反数. (简称:纵轴纵相等)
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(-x, y)
(x, -y)
探索与思考
如图,四边形ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4),画出四边形ABCD 关于y 轴对称的图形。
x
y
1
1
O
A
B
C
D
A’
B’
C’
D’
尝试画出四边形ABCD 关于x 轴对称的图形
练一练
1、点(-5,7)关于y轴对称点为_________;
2、点(-2,1)关于x轴对称点为_________;
3、点(1,2)关于y轴对称点为__________;
4、点A(a,-5)与点B(-2,b)
1)关于x轴对称则a=_____, b=______;
1)关于y轴对称则a=_____, b=______;
2
-5
(-1,2)
(5,7)
(-2,-1)
-2
5
练一练
已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴对称点的坐标分别为
A’(3,5),B’(4,1),C’(1,3).
依次连接A’B’,B’C’,C’A’,
就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
y
x
练一练
1.(1)分别写出下列各点关于x轴对称点的坐标:
A(3,6),B(﹣7,9),C(6,﹣1)
(2)分别写出下列各点关于y轴对称点的坐标:
D(﹣3,﹣5),E(0,10),F(8,0)
解:(1)A(3,6)关于x轴对称点的坐标是(3,﹣6),
B(﹣7,9)关于x轴对称点的坐标是(﹣7,﹣9),
C(6,﹣1)关于x轴对称点的坐标是(6,1);
(2)D(﹣3,﹣5)关于y轴对称点的坐标为(3,﹣5),
E(0,10)关于y轴对称点的坐标为(0,10),
F(8,0)关于y轴对称点的坐标为(﹣8,0).
练一练
2.已知点P(a,a-b)在第四象限,求:
(1)点M(-a,b)所在的象限:
(2)点M分别关于x轴、y轴、原点的对称点M 1 、M 2 、M 3 的坐标:
(3)若a=b,P点和M点所在的位置.
解:(1)∵点P(a,a-b)在第四象限, ∴a>0,a-b<0 ,
∴b>a>0,-a<0 ,∴M(-a,b)在第二象限.
(2)∵M 1 、M 2 、M 3 与M(-a,b)关于x轴、y轴、原点对称,
∴M 1 (-a,-b)、M 2 (a,b)、M 3 (a,-b).
(3)当a=b时,P点的坐标为(a,0),M(-a,a).
∵a>0, ∴P点在x轴的正半轴上,M点在第二象限角平分线上(除去原点).
练一练
3.已知点A(2m+n,2),B (1,n-m),当 m、n 分别为何值时,
(1)A、B 关于 x 轴对称;
(2)A、B 关于 y 轴对称.
解:点,B,A、B关于x轴对称,
,解得;
点,B,A、B关于y轴对称,
,解得:.
课后回顾
关于x轴对称点
的坐标特征
01
课后回顾
关于y轴对称点
的坐标特征
02
在平面直角坐标系中作出一个图形关于x、y轴的轴对称图形
03
谢谢~
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
画轴对称图形
课前回顾
轴对称图形的做法:
1、几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形.
2、对于一些由直线、线段或射线组成的图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形。
学习目标
学习目标
1.能知道关于x轴或关于y轴对称的点的坐标特征。
2. 能利用对称点坐标规律在平面直角坐标系中作出一个图形关于x、y轴的轴对称图形。
重点
掌握关于坐标轴对称的点的坐标规律。
难点
在平面直角坐标系中作出一个图形关于x、y轴的轴对称图形。
观察与思考
下图是一张北京城的示意图,假如以天安门为原点,分别以长安街和中轴线为x 轴和y 轴建立平面直角坐标系,对应于东直门的坐标,你能找到西直门的位置吗?并说出西直门的坐标.
(-3.5,4)
观察与思考
如图,在平面直角坐标系中你能画出点A关于x轴、y轴的对称点吗
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
A’(2,-3)
A’’ (-2,3)
观察与思考
画出下列已知点及其关于对称轴的对称点。你发现了什么?
已知点 A(2,-3) B(-1,2) C(4,0) D(0,0)
关于x轴的对称点
关于y轴的对称点
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A ’(2,3)
A ” (-2,-3)
B ’(-1,-2)
B ” (1,2)
C ’(4,0)
C” (-4,0)
D ’(0,0)
D ” (0,0)
A
B
C
D
再找几个点,分别画出它们的对称点,检验一下你发现的规律。
小结
1.关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数. (简称:横轴横相等)
2.关于y轴对称的点的坐标的特点是:
纵坐标相等,横坐标互为相反数. (简称:纵轴纵相等)
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(-x, y)
(x, -y)
探索与思考
如图,四边形ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4),画出四边形ABCD 关于y 轴对称的图形。
x
y
1
1
O
A
B
C
D
A’
B’
C’
D’
尝试画出四边形ABCD 关于x 轴对称的图形
练一练
1、点(-5,7)关于y轴对称点为_________;
2、点(-2,1)关于x轴对称点为_________;
3、点(1,2)关于y轴对称点为__________;
4、点A(a,-5)与点B(-2,b)
1)关于x轴对称则a=_____, b=______;
1)关于y轴对称则a=_____, b=______;
2
-5
(-1,2)
(5,7)
(-2,-1)
-2
5
练一练
已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴对称点的坐标分别为
A’(3,5),B’(4,1),C’(1,3).
依次连接A’B’,B’C’,C’A’,
就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
y
x
练一练
1.(1)分别写出下列各点关于x轴对称点的坐标:
A(3,6),B(﹣7,9),C(6,﹣1)
(2)分别写出下列各点关于y轴对称点的坐标:
D(﹣3,﹣5),E(0,10),F(8,0)
解:(1)A(3,6)关于x轴对称点的坐标是(3,﹣6),
B(﹣7,9)关于x轴对称点的坐标是(﹣7,﹣9),
C(6,﹣1)关于x轴对称点的坐标是(6,1);
(2)D(﹣3,﹣5)关于y轴对称点的坐标为(3,﹣5),
E(0,10)关于y轴对称点的坐标为(0,10),
F(8,0)关于y轴对称点的坐标为(﹣8,0).
练一练
2.已知点P(a,a-b)在第四象限,求:
(1)点M(-a,b)所在的象限:
(2)点M分别关于x轴、y轴、原点的对称点M 1 、M 2 、M 3 的坐标:
(3)若a=b,P点和M点所在的位置.
解:(1)∵点P(a,a-b)在第四象限, ∴a>0,a-b<0 ,
∴b>a>0,-a<0 ,∴M(-a,b)在第二象限.
(2)∵M 1 、M 2 、M 3 与M(-a,b)关于x轴、y轴、原点对称,
∴M 1 (-a,-b)、M 2 (a,b)、M 3 (a,-b).
(3)当a=b时,P点的坐标为(a,0),M(-a,a).
∵a>0, ∴P点在x轴的正半轴上,M点在第二象限角平分线上(除去原点).
练一练
3.已知点A(2m+n,2),B (1,n-m),当 m、n 分别为何值时,
(1)A、B 关于 x 轴对称;
(2)A、B 关于 y 轴对称.
解:点,B,A、B关于x轴对称,
,解得;
点,B,A、B关于y轴对称,
,解得:.
课后回顾
关于x轴对称点
的坐标特征
01
课后回顾
关于y轴对称点
的坐标特征
02
在平面直角坐标系中作出一个图形关于x、y轴的轴对称图形
03
谢谢~
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
