17.1勾股定理 课后强化练习 人教版八年级数学下册(无答案)
文档属性
| 名称 | 17.1勾股定理 课后强化练习 人教版八年级数学下册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 301.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 22:19:21 | ||
图片预览


文档简介
《17.1勾股定理》课后强化
班级:________ 姓名:________
一、单选题(共 10 小题)
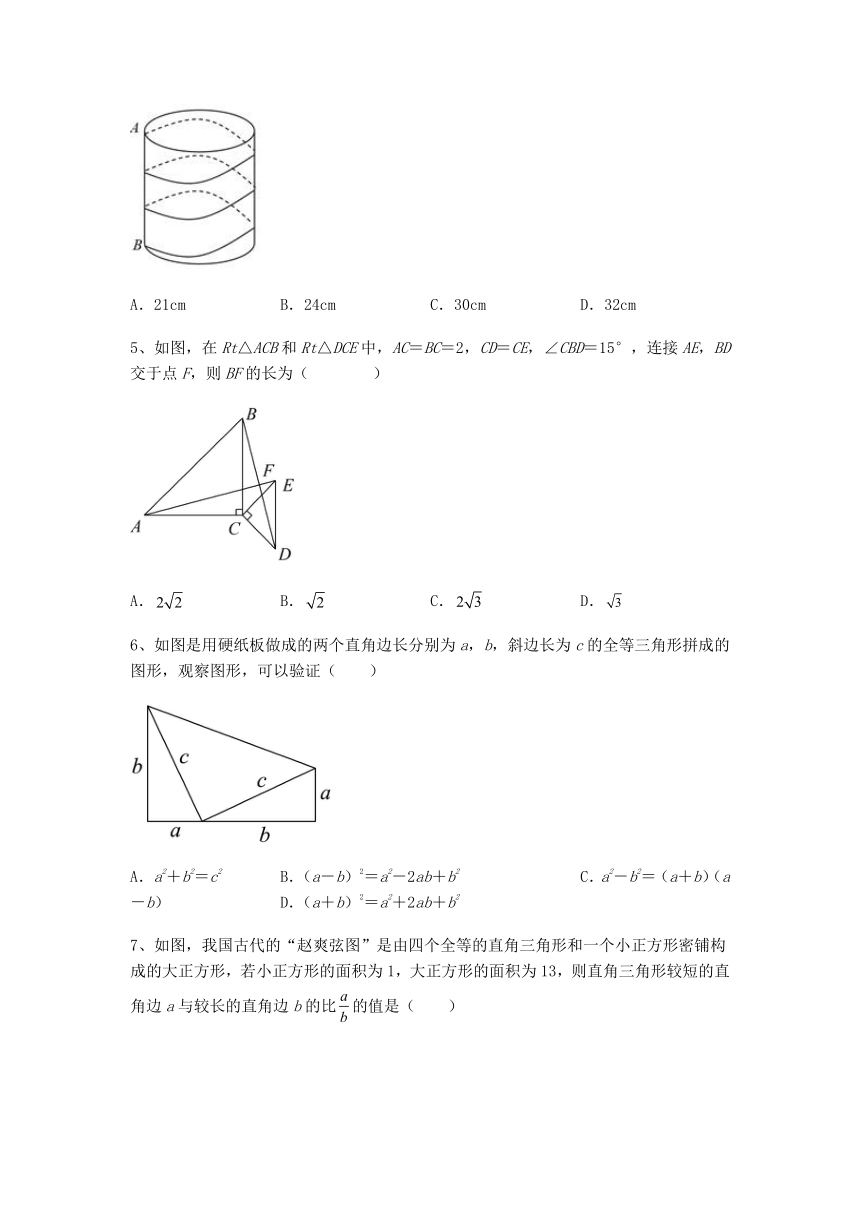
1、如图,,,AD平分交BC于点D,交AC于点E,已知,,则AD长为( )
A.7 B.8 C. D.
2、当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
4、如图,圆柱底面半径为,高为18cm,点A、B分别是圆柱两底面圆周上的点,且点B在点A的正上方,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.21cm B.24cm C.30cm D.32cm
5、如图,在Rt△ACB和Rt△DCE中,AC=BC=2,CD=CE,∠CBD=15°,连接AE,BD交于点F,则BF的长为( )
A. B. C. D.
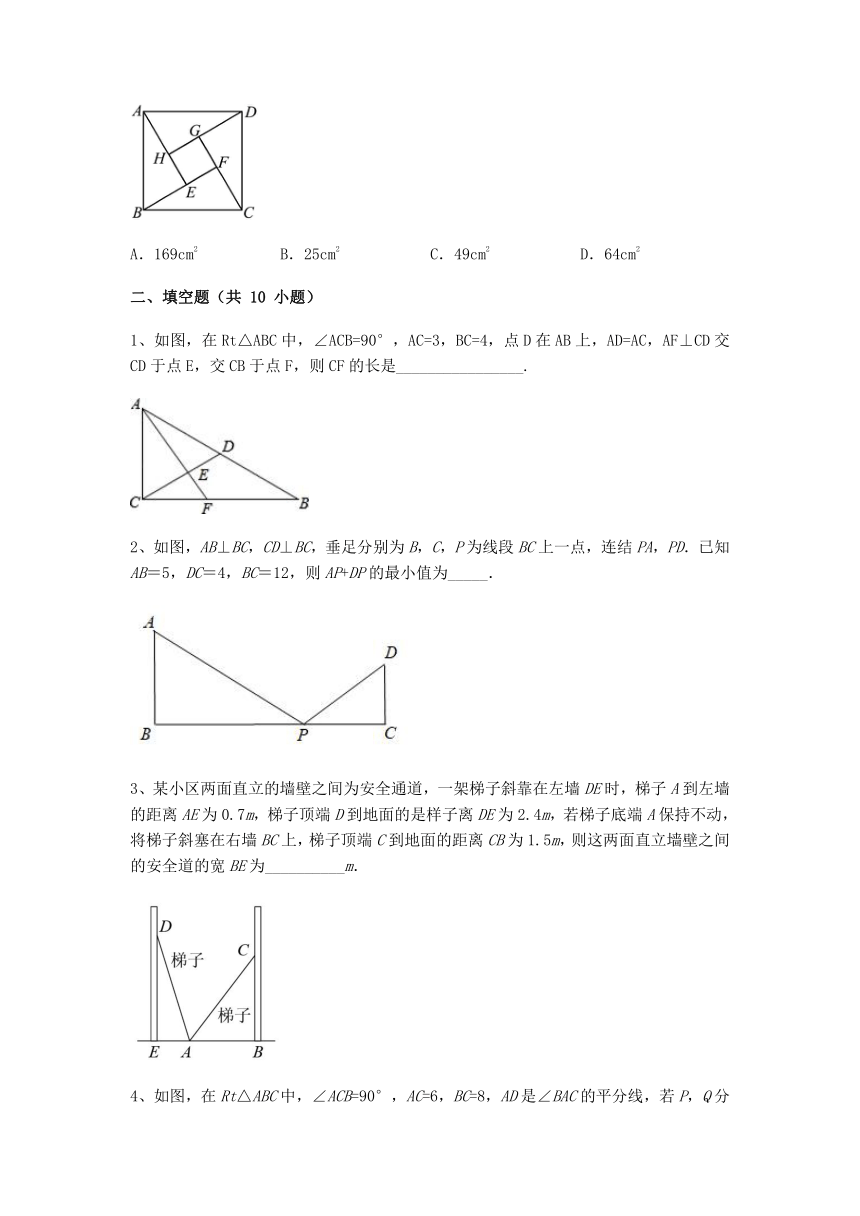
6、如图是用硬纸板做成的两个直角边长分别为a,b,斜边长为c的全等三角形拼成的图形,观察图形,可以验证( )
A.a2+b2=c2 B.(a-b)2=a2-2ab+b2 C.a2-b2=(a+b)(a-b) D.(a+b)2=a2+2ab+b2
7、如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比的值是( )
A. B. C. D.
8、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底墙到左墙角的距离为1.5m,顶端距离地面2m,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面0.7m,那么小巷的宽度为( )
A.3.2m B.3.5m C.3.9m D.4m
9、如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边BC的两个“黄金分割”点,则△ADE的面积为( )
A.10﹣4 B.3﹣5 C. D.20﹣8
10、如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠AEB=90°,AB=13cm,BE=5cm,则阴影部分的面积是( )
A.169cm2 B.25cm2 C.49cm2 D.64cm2
二、填空题(共 10 小题)
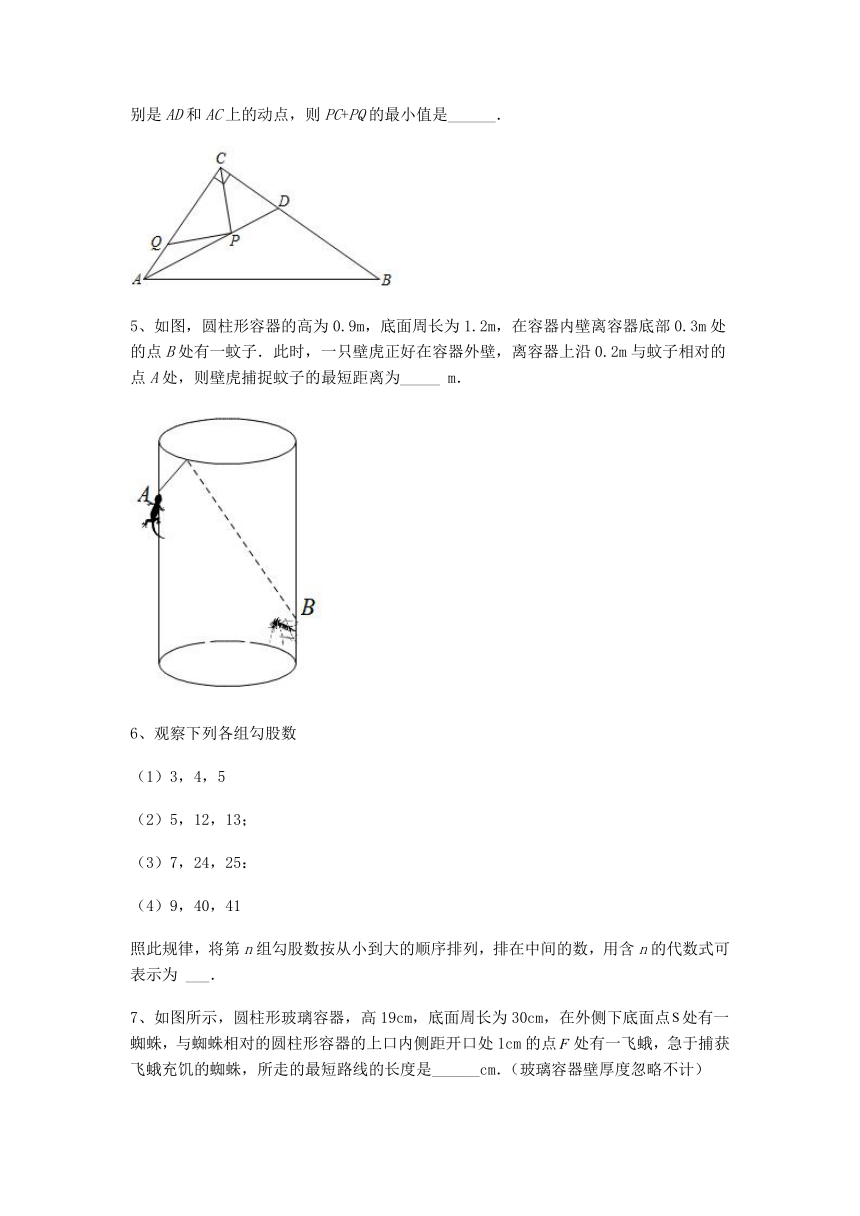
1、如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.
2、如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连结PA,PD.已知AB=5,DC=4,BC=12,则AP+DP的最小值为_____.
3、某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子A到左墙的距离AE为0.7m,梯子顶端D到地面的是样子离DE为2.4m,若梯子底端A保持不动,将梯子斜塞在右墙BC上,梯子顶端C到地面的距离CB为1.5m,则这两面直立墙壁之间的安全道的宽BE为__________m.
4、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是______.
5、如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_____ m.
6、观察下列各组勾股数
(1)3,4,5
(2)5,12,13;
(3)7,24,25:
(4)9,40,41
照此规律,将第n组勾股数按从小到大的顺序排列,排在中间的数,用含n的代数式可表示为 ___.
7、如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点处有一飞蛾,急于捕获飞蛾充饥的蜘蛛,所走的最短路线的长度是______cm.(玻璃容器壁厚度忽略不计)
8、如图,在中,,将线段绕点顺时针旋转至,过点作,垂足为,若,,则的长为__.
9、如图,铁路MN和公路PQ在O点处交汇,公路PQ上A处点距离O点240米,距离MN 120米,如果火车行驶时,周围两百米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向,以144千米/时的速度行驶时,A处受噪音影响的时间是_______s
10、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为________.
三、解答题(共 6 小题)
1、如图△ABC中,∠ACB=90°,AC=12,BC=5.
(1)求AB的长;
(2)若动点P从点C开始以每秒1个单位的速度,按C→A→B的路径运动,设运动的时间为t秒,当t为何值时,△BCP为等腰三角形?
2、如图,点是数轴上表示实数的点.
(1)用直尺和圆规在数轴上作出表示实数的的点;(保留作图痕迹,不写作法)
(2)利用数轴比较和的大小,并说明理由.
3、在△ABC中,AB=AC,CD⊥AB于D.
(1)若∠A=40°,求∠DCB的度数;
(2)若BC=15,CD=12,求AC的长.
4、我国在防控新冠疫情上取得重大成绩,但新冠疫情在国外开始蔓延,为了防止境外输入病例的增加,我国暂时停止了一切国际航班、水运.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我国海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,6分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡航艇的航向为北偏西.
(1)求甲巡逻艇的航行方向(用含n的式子表示)
(2)成功拦截后,甲、乙两艘巡逻艇同时沿原方向返回且速度不变,3分钟后甲、乙两艘巡逻艇相距多少海里?
5、中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
6、已知中,,,,P、Q是边上的两个动点,其中点P从点A开始沿方向运动且速度为每秒2cm,点Q从点B开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒,
(1)线段________;
(2)当秒时,求的面积;
(3)当点时,________;
(4)若将周长分为两部分,直接写出t的值.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,,,AD平分交BC于点D,交AC于点E,已知,,则AD长为( )
A.7 B.8 C. D.
2、当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
4、如图,圆柱底面半径为,高为18cm,点A、B分别是圆柱两底面圆周上的点,且点B在点A的正上方,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.21cm B.24cm C.30cm D.32cm
5、如图,在Rt△ACB和Rt△DCE中,AC=BC=2,CD=CE,∠CBD=15°,连接AE,BD交于点F,则BF的长为( )
A. B. C. D.
6、如图是用硬纸板做成的两个直角边长分别为a,b,斜边长为c的全等三角形拼成的图形,观察图形,可以验证( )
A.a2+b2=c2 B.(a-b)2=a2-2ab+b2 C.a2-b2=(a+b)(a-b) D.(a+b)2=a2+2ab+b2
7、如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比的值是( )
A. B. C. D.
8、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底墙到左墙角的距离为1.5m,顶端距离地面2m,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面0.7m,那么小巷的宽度为( )
A.3.2m B.3.5m C.3.9m D.4m
9、如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边BC的两个“黄金分割”点,则△ADE的面积为( )
A.10﹣4 B.3﹣5 C. D.20﹣8
10、如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠AEB=90°,AB=13cm,BE=5cm,则阴影部分的面积是( )
A.169cm2 B.25cm2 C.49cm2 D.64cm2
二、填空题(共 10 小题)
1、如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.
2、如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连结PA,PD.已知AB=5,DC=4,BC=12,则AP+DP的最小值为_____.
3、某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子A到左墙的距离AE为0.7m,梯子顶端D到地面的是样子离DE为2.4m,若梯子底端A保持不动,将梯子斜塞在右墙BC上,梯子顶端C到地面的距离CB为1.5m,则这两面直立墙壁之间的安全道的宽BE为__________m.
4、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是______.
5、如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_____ m.
6、观察下列各组勾股数
(1)3,4,5
(2)5,12,13;
(3)7,24,25:
(4)9,40,41
照此规律,将第n组勾股数按从小到大的顺序排列,排在中间的数,用含n的代数式可表示为 ___.
7、如图所示,圆柱形玻璃容器,高19cm,底面周长为30cm,在外侧下底面点处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点处有一飞蛾,急于捕获飞蛾充饥的蜘蛛,所走的最短路线的长度是______cm.(玻璃容器壁厚度忽略不计)
8、如图,在中,,将线段绕点顺时针旋转至,过点作,垂足为,若,,则的长为__.
9、如图,铁路MN和公路PQ在O点处交汇,公路PQ上A处点距离O点240米,距离MN 120米,如果火车行驶时,周围两百米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向,以144千米/时的速度行驶时,A处受噪音影响的时间是_______s
10、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为________.
三、解答题(共 6 小题)
1、如图△ABC中,∠ACB=90°,AC=12,BC=5.
(1)求AB的长;
(2)若动点P从点C开始以每秒1个单位的速度,按C→A→B的路径运动,设运动的时间为t秒,当t为何值时,△BCP为等腰三角形?
2、如图,点是数轴上表示实数的点.
(1)用直尺和圆规在数轴上作出表示实数的的点;(保留作图痕迹,不写作法)
(2)利用数轴比较和的大小,并说明理由.
3、在△ABC中,AB=AC,CD⊥AB于D.
(1)若∠A=40°,求∠DCB的度数;
(2)若BC=15,CD=12,求AC的长.
4、我国在防控新冠疫情上取得重大成绩,但新冠疫情在国外开始蔓延,为了防止境外输入病例的增加,我国暂时停止了一切国际航班、水运.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我国海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,6分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡航艇的航向为北偏西.
(1)求甲巡逻艇的航行方向(用含n的式子表示)
(2)成功拦截后,甲、乙两艘巡逻艇同时沿原方向返回且速度不变,3分钟后甲、乙两艘巡逻艇相距多少海里?
5、中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
6、已知中,,,,P、Q是边上的两个动点,其中点P从点A开始沿方向运动且速度为每秒2cm,点Q从点B开始沿方向运动,在边上的运动速度是每秒,在边上的运动速度是每秒,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒,
(1)线段________;
(2)当秒时,求的面积;
(3)当点时,________;
(4)若将周长分为两部分,直接写出t的值.
