山东省济南市莱芜区2022-2023学年高一下学期6月月考数学试题(含答案)
文档属性
| 名称 | 山东省济南市莱芜区2022-2023学年高一下学期6月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 19:53:51 | ||
图片预览


文档简介
济南市莱芜区2022-2023学年高一下学期6月月考
数学试题
2023.06
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,答题时间120分钟.
注意事项:
1.答第Ⅰ卷前,考生务必将自己的级部、班级、姓名、准考证号、写在答题纸密封线外,并将姓名、准考证号、考试科目、试卷类型填涂在答题卡上.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.
3.考试结束后将答题卡交回.
第I卷(选择题 共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每题给出的四个选项中,只有一项是最符合题意的.
1.若复数(为虚数单位),则( )
A.1 B.2 C. D.
2.设,为两个不同的平面,,为两条不同的直线,下列命题正确的是( )
A.若,,则 B.若,,,则
C.若,,则 D.若,,,则
3.在中,若,,,则此三角形解的情况是( )
A.有一解 B.有两解 C.无解 D.有解但解的个数不确定
4.若向量,满足,,且,则向量与夹角的余弦值为( )
A. B. C. D.
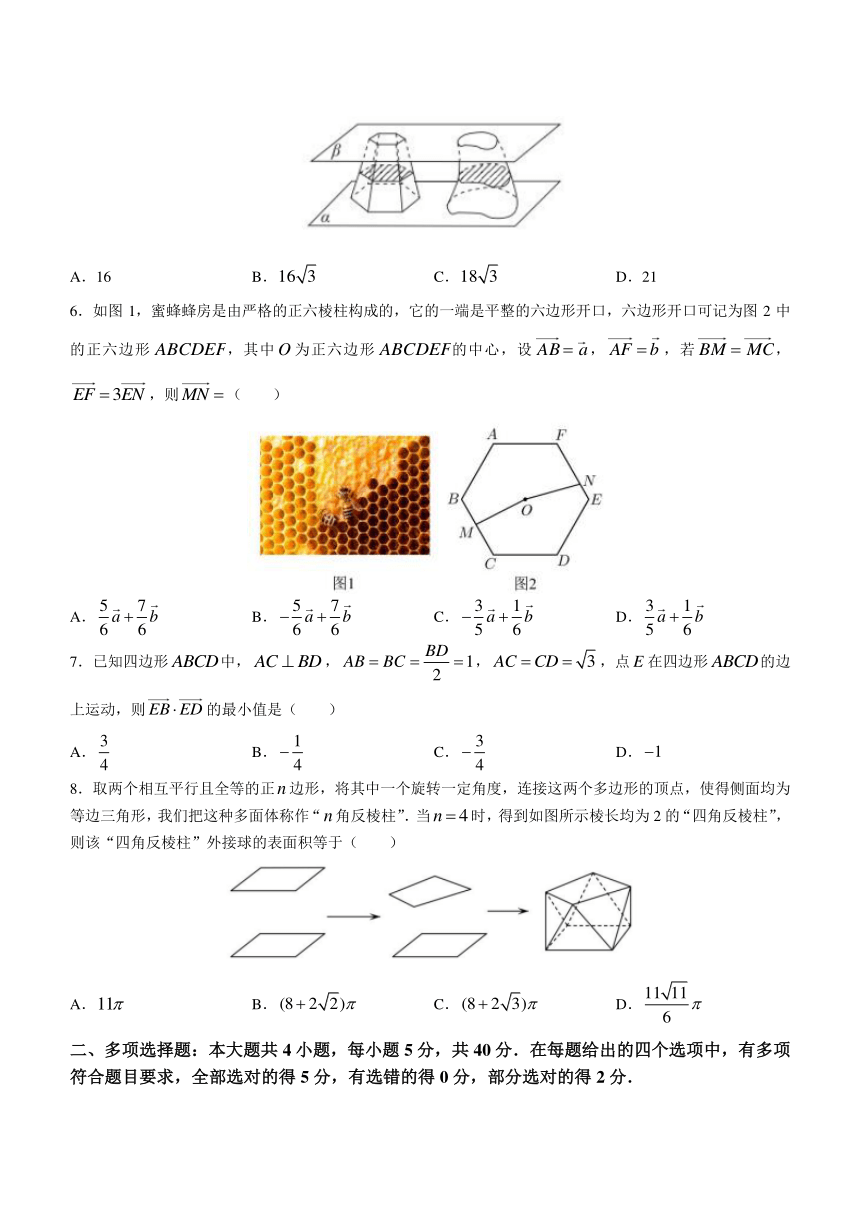
5.中国南北朝时期数学家、天文学家祖冲之、祖暅父子总结了魏晋时期著名数学家刘徽的有关工作,提出“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.即界于两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等.上述原理在中国被称为祖暅原理.一个上底面边长为1,下底面边长为2,高为的正六棱台与一个不规则几何体满足“幂势既同”,则该不规则几何体的体积为( )
A.16 B. C. D.21
6.如图1,蜜蜂蜂房是由严格的正六棱柱构成的,它的一端是平整的六边形开口,六边形开口可记为图2中的正六边形,其中为正六边形的中心,设,,若,,则( )
A. B. C. D.
7.已知四边形中,,,,点在四边形的边上运动,则的最小值是( )
A. B. C. D.
8.取两个相互平行且全等的正边形,将其中一个旋转一定角度,连接这两个多边形的顶点,使得侧面均为等边三角形,我们把这种多面体称作“角反棱柱”.当时,得到如图所示棱长均为2的“四角反棱柱”,则该“四角反棱柱”外接球的表面积等于( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共40分.在每题给出的四个选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.下面是关于复数(为虚数单位)的命题,其中真命题为( )
A.的虚部为 B.若,则的最大值是
C.的共轭复数为 D.在复平面内对应的点在第二象限
10.下列说法正确的是( )
A.若,,则
B.两个非零向量和,若,则与垂直
C.若,则是的垂心
D.已知,,若在上的投影向量为(为与同向的单位向量),则
11.在中,角,,所对的边分别为,,,,,为外接圆圆心,为的中点.则下列结论正确的有( )
A. B.外接圆面积为
C. D.的最大值为
12.如图1,在边长为2的正方形中,,分别为,的中点,沿、及把这个正方形折成一个四面体,使得、、三点重合于点,得到四面体(如图2).下列结论正确的是( )
A.平面平面 B.四面体的体积为
C.二面角正切值为 D.顶点在底面上的射影为的垂心
第Ⅱ卷(非选择题 共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.已知圆锥侧面展开图扇形的圆心角为,底面圆的半径为1,则圆锥的体积为________.
14.已知向量,的夹角的余弦值为,,且与垂直,则________.
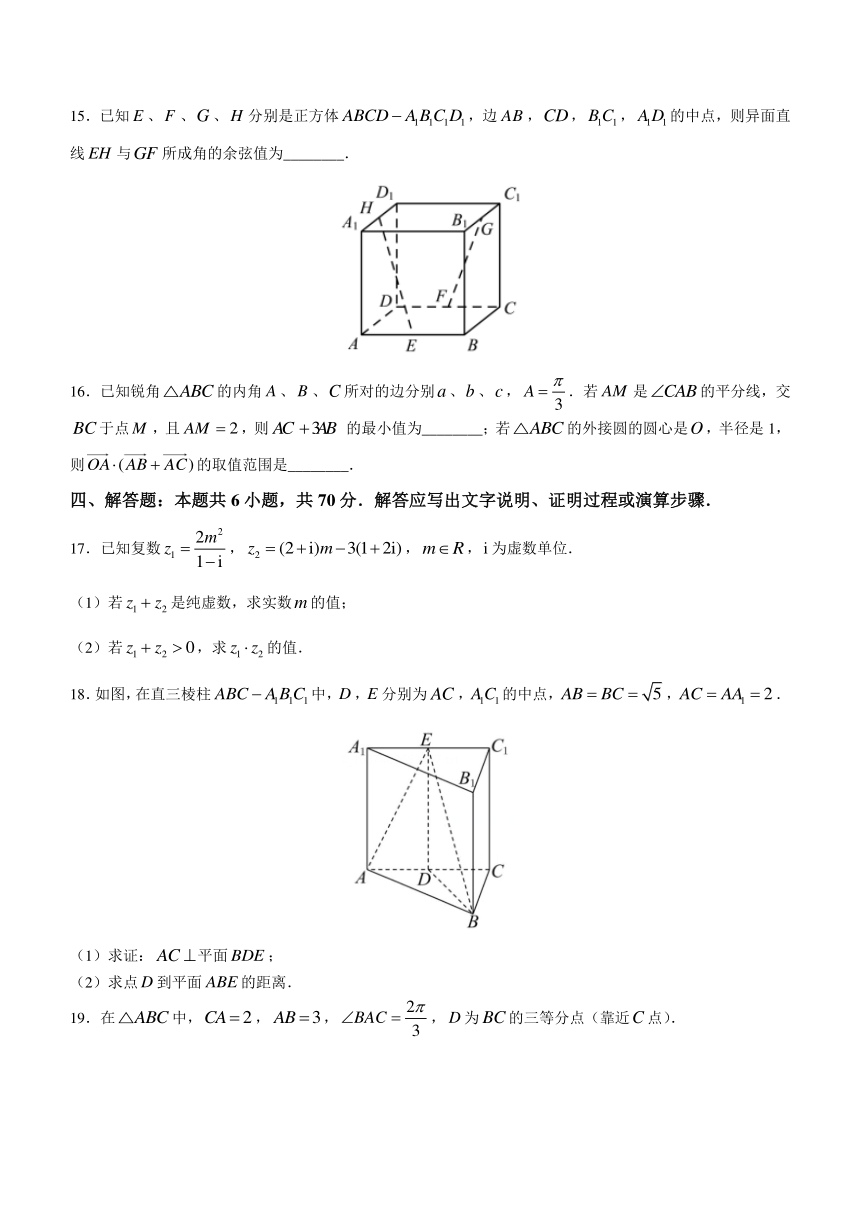
15.已知、、、分别是正方体,边,,,的中点,则异面直线与所成角的余弦值为________.
16.已知锐角的内角、、所对的边分别、、,.若是的平分线,交于点,且,则的最小值为________;若的外接圆的圆心是,半径是1,则的取值范围是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知复数,,,为虚数单位.
(1)若是纯虚数,求实数的值;
(2)若,求的值.
18.如图,在直三棱柱中,,分别为,的中点,,.
(1)求证:平面;
(2)求点到平面的距离.
19.在中,,,,为的三等分点(靠近点).
(1)求的值;
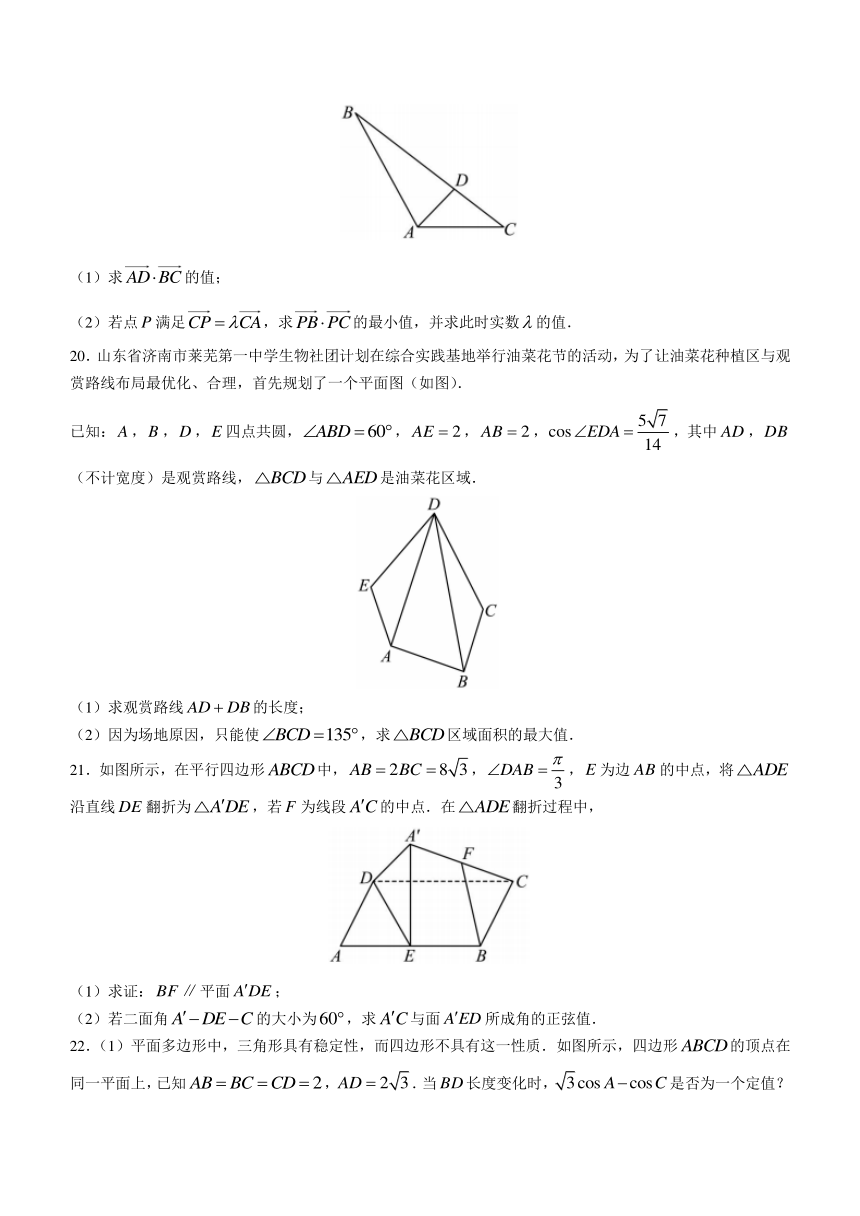
(2)若点满足,求的最小值,并求此时实数的值.
20.山东省济南市莱芜第一中学生物社团计划在综合实践基地举行油菜花节的活动,为了让油菜花种植区与观赏路线布局最优化、合理,首先规划了一个平面图(如图).
已知:,,,四点共圆,,,,,其中,(不计宽度)是观赏路线,与是油菜花区域.
(1)求观赏路线的长度;
(2)因为场地原因,只能使,求区域面积的最大值.
21.如图所示,在平行四边形中,,,为边的中点,将沿直线翻折为,若为线段的中点.在翻折过程中,
(1)求证:平面;
(2)若二面角的大小为,求与面所成角的正弦值.
22.(1)平面多边形中,三角形具有稳定性,而四边形不具有这一性质.如图所示,四边形的顶点在同一平面上,已知,.当长度变化时,是否为一个定值?若是,求出这个定值;若否,说明理由.
(2)记的内角,,的对边分别为,,,已知,求的取值范围.
济南市莱芜区2022-2023学年高一下学期6月月考
数学答案
一、单项选择题.
1.D 2.C 3.B 4.D 5.D 6.B 7.C 8.B
【参考解法(不唯一)】7.C 【详解】如图所示,因为,且,所以垂直且平分,
则为等腰三角形,又,所以为等边三角形,
则四边形关于直线对称,
故点在四边形上运动时,只需考虑点在边,上的运动情况即可,
因为,,知,
即,则,
①当点在边上运动时,设,则,则
,
当时,最小值为;
②当点在边上运动时,
设,则,
则,
当时,的最小值为;综上,的最小值为;
8.B 如图所示:设上下底面的中心分别为,,设该“四角反棱柱”外接球的球心是,
显然是的中点,设的中点为,连接,,过做,垂足为,
因为,,所以,
在直角三角形中,,
所以有,于是有,在直角三角形中,
,
所以该“四角反棱柱”外接球的表面积等于,
二、多项选择题.
9.BC; 10.BC; 11.ACD; 12.BD
12.BD 【详解】如图,作的中点,连结、,过作的垂线交于点,连结,过作的垂线交于点,连结
由题知,所以,,所以,
∴为平面与平面的二面角的平面角
又∴平面,平面,∴,
作法知,,∴平面,
所以为锥体的高.所以为在平面上的射影.平面,所以,
由作法知, ∴平面,平面,∴
∴为平面与平面的二面角的平面角,显然为锐角,故A错.
由题知平面,平面,∴
又,,,∴,
,四面体的体积为,故B正确.
在直角三角形中: 故C不正确.
因为,,
所以,
∴,由对称性知,又 故D正确.
三、填空题.
13. 14. 15. 16.
16.【详解】(1)由是的平分线,得,又∵,
即,化简得,
∴,
当且仅当,即,时,取等号.
(2)∵,,∴
,
∵是锐角三角形,∴,
∴, ∴,∴.
四、解答题.
17.(1),,
所以,
因为是纯虚数,所以,得.
(2)由(1)知,,因为,所以,得,
所以,,所以.
18.(1)证明:∵,,分别为,的中点,
∴,且,又平面,∴平面,
又平面,∴,
又,且,,平面,∴平面.
(2)∵,,,∴,
∴,,.
在中,,,∴边上的高为.
∴.设点到平面的距离为,
根据,得,解得,
所以点到平面的距离为.
19.【详解】(1)因为为的三等分点(靠近点),所以,
所以,
所以
.
(2)因为,所以,因为,
所以
,
所以当时,取得最小值.
20.(1)∵,,,四点共圆,,∴,
∵,∴;
在中,由正弦定理得:,
∵,,,∴;
在中,由余弦定理知:,
即,解得:或(舍),∴.
(2)在中,,∴;
在中,由余弦定理得:,
∴(当且仅当时取等号),
∴,∴,即区域面积的最大值为.
21.(1)证明:取的中点,连接,,
∵为线段的中点,∴,
∵平面,平面,∴平面,
又,,∴四边形为平行四边形,则.平面,平面,可得平面,
又,,平面,可得平面平面,平面,
则面.
(2)取中点,中点,连接,,,
由,,为边的中点,
得,所以为等边三角形,从而,,
又,为的中点,所以,又是等边三角形,
所以,所以为二面角的平面角,所以,
过点作,过作交于,连接,
∵是等边三角形,所以可求得,,
所以,,∵,,,,
所以,,又,,面,
所以面,又,所以面,
∵平面,所以面面,
由,在中易求得,又,所以,,
面面,面,所以面,
所以为与平面所成的角,
在中可求得,所以,
∴与面所成角的正弦值为.
22.【详解】(1)在中,由余弦定理,
即①,同理,在中,,即②,
①②得,所以当长度变化时,为定值,定值为1;
(2),为的内角,则
则由,可得,则、均为锐角
又,,则,
则,则
则
令,则
又在单调递增,,
可得,则的取值范围为,
则的取值范围为
数学试题
2023.06
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,答题时间120分钟.
注意事项:
1.答第Ⅰ卷前,考生务必将自己的级部、班级、姓名、准考证号、写在答题纸密封线外,并将姓名、准考证号、考试科目、试卷类型填涂在答题卡上.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.
3.考试结束后将答题卡交回.
第I卷(选择题 共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每题给出的四个选项中,只有一项是最符合题意的.
1.若复数(为虚数单位),则( )
A.1 B.2 C. D.
2.设,为两个不同的平面,,为两条不同的直线,下列命题正确的是( )
A.若,,则 B.若,,,则
C.若,,则 D.若,,,则
3.在中,若,,,则此三角形解的情况是( )
A.有一解 B.有两解 C.无解 D.有解但解的个数不确定
4.若向量,满足,,且,则向量与夹角的余弦值为( )
A. B. C. D.
5.中国南北朝时期数学家、天文学家祖冲之、祖暅父子总结了魏晋时期著名数学家刘徽的有关工作,提出“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.即界于两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等.上述原理在中国被称为祖暅原理.一个上底面边长为1,下底面边长为2,高为的正六棱台与一个不规则几何体满足“幂势既同”,则该不规则几何体的体积为( )
A.16 B. C. D.21
6.如图1,蜜蜂蜂房是由严格的正六棱柱构成的,它的一端是平整的六边形开口,六边形开口可记为图2中的正六边形,其中为正六边形的中心,设,,若,,则( )
A. B. C. D.
7.已知四边形中,,,,点在四边形的边上运动,则的最小值是( )
A. B. C. D.
8.取两个相互平行且全等的正边形,将其中一个旋转一定角度,连接这两个多边形的顶点,使得侧面均为等边三角形,我们把这种多面体称作“角反棱柱”.当时,得到如图所示棱长均为2的“四角反棱柱”,则该“四角反棱柱”外接球的表面积等于( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共40分.在每题给出的四个选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.下面是关于复数(为虚数单位)的命题,其中真命题为( )
A.的虚部为 B.若,则的最大值是
C.的共轭复数为 D.在复平面内对应的点在第二象限
10.下列说法正确的是( )
A.若,,则
B.两个非零向量和,若,则与垂直
C.若,则是的垂心
D.已知,,若在上的投影向量为(为与同向的单位向量),则
11.在中,角,,所对的边分别为,,,,,为外接圆圆心,为的中点.则下列结论正确的有( )
A. B.外接圆面积为
C. D.的最大值为
12.如图1,在边长为2的正方形中,,分别为,的中点,沿、及把这个正方形折成一个四面体,使得、、三点重合于点,得到四面体(如图2).下列结论正确的是( )
A.平面平面 B.四面体的体积为
C.二面角正切值为 D.顶点在底面上的射影为的垂心
第Ⅱ卷(非选择题 共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.已知圆锥侧面展开图扇形的圆心角为,底面圆的半径为1,则圆锥的体积为________.
14.已知向量,的夹角的余弦值为,,且与垂直,则________.
15.已知、、、分别是正方体,边,,,的中点,则异面直线与所成角的余弦值为________.
16.已知锐角的内角、、所对的边分别、、,.若是的平分线,交于点,且,则的最小值为________;若的外接圆的圆心是,半径是1,则的取值范围是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知复数,,,为虚数单位.
(1)若是纯虚数,求实数的值;
(2)若,求的值.
18.如图,在直三棱柱中,,分别为,的中点,,.
(1)求证:平面;
(2)求点到平面的距离.
19.在中,,,,为的三等分点(靠近点).
(1)求的值;
(2)若点满足,求的最小值,并求此时实数的值.
20.山东省济南市莱芜第一中学生物社团计划在综合实践基地举行油菜花节的活动,为了让油菜花种植区与观赏路线布局最优化、合理,首先规划了一个平面图(如图).
已知:,,,四点共圆,,,,,其中,(不计宽度)是观赏路线,与是油菜花区域.
(1)求观赏路线的长度;
(2)因为场地原因,只能使,求区域面积的最大值.
21.如图所示,在平行四边形中,,,为边的中点,将沿直线翻折为,若为线段的中点.在翻折过程中,
(1)求证:平面;
(2)若二面角的大小为,求与面所成角的正弦值.
22.(1)平面多边形中,三角形具有稳定性,而四边形不具有这一性质.如图所示,四边形的顶点在同一平面上,已知,.当长度变化时,是否为一个定值?若是,求出这个定值;若否,说明理由.
(2)记的内角,,的对边分别为,,,已知,求的取值范围.
济南市莱芜区2022-2023学年高一下学期6月月考
数学答案
一、单项选择题.
1.D 2.C 3.B 4.D 5.D 6.B 7.C 8.B
【参考解法(不唯一)】7.C 【详解】如图所示,因为,且,所以垂直且平分,
则为等腰三角形,又,所以为等边三角形,
则四边形关于直线对称,
故点在四边形上运动时,只需考虑点在边,上的运动情况即可,
因为,,知,
即,则,
①当点在边上运动时,设,则,则
,
当时,最小值为;
②当点在边上运动时,
设,则,
则,
当时,的最小值为;综上,的最小值为;
8.B 如图所示:设上下底面的中心分别为,,设该“四角反棱柱”外接球的球心是,
显然是的中点,设的中点为,连接,,过做,垂足为,
因为,,所以,
在直角三角形中,,
所以有,于是有,在直角三角形中,
,
所以该“四角反棱柱”外接球的表面积等于,
二、多项选择题.
9.BC; 10.BC; 11.ACD; 12.BD
12.BD 【详解】如图,作的中点,连结、,过作的垂线交于点,连结,过作的垂线交于点,连结
由题知,所以,,所以,
∴为平面与平面的二面角的平面角
又∴平面,平面,∴,
作法知,,∴平面,
所以为锥体的高.所以为在平面上的射影.平面,所以,
由作法知, ∴平面,平面,∴
∴为平面与平面的二面角的平面角,显然为锐角,故A错.
由题知平面,平面,∴
又,,,∴,
,四面体的体积为,故B正确.
在直角三角形中: 故C不正确.
因为,,
所以,
∴,由对称性知,又 故D正确.
三、填空题.
13. 14. 15. 16.
16.【详解】(1)由是的平分线,得,又∵,
即,化简得,
∴,
当且仅当,即,时,取等号.
(2)∵,,∴
,
∵是锐角三角形,∴,
∴, ∴,∴.
四、解答题.
17.(1),,
所以,
因为是纯虚数,所以,得.
(2)由(1)知,,因为,所以,得,
所以,,所以.
18.(1)证明:∵,,分别为,的中点,
∴,且,又平面,∴平面,
又平面,∴,
又,且,,平面,∴平面.
(2)∵,,,∴,
∴,,.
在中,,,∴边上的高为.
∴.设点到平面的距离为,
根据,得,解得,
所以点到平面的距离为.
19.【详解】(1)因为为的三等分点(靠近点),所以,
所以,
所以
.
(2)因为,所以,因为,
所以
,
所以当时,取得最小值.
20.(1)∵,,,四点共圆,,∴,
∵,∴;
在中,由正弦定理得:,
∵,,,∴;
在中,由余弦定理知:,
即,解得:或(舍),∴.
(2)在中,,∴;
在中,由余弦定理得:,
∴(当且仅当时取等号),
∴,∴,即区域面积的最大值为.
21.(1)证明:取的中点,连接,,
∵为线段的中点,∴,
∵平面,平面,∴平面,
又,,∴四边形为平行四边形,则.平面,平面,可得平面,
又,,平面,可得平面平面,平面,
则面.
(2)取中点,中点,连接,,,
由,,为边的中点,
得,所以为等边三角形,从而,,
又,为的中点,所以,又是等边三角形,
所以,所以为二面角的平面角,所以,
过点作,过作交于,连接,
∵是等边三角形,所以可求得,,
所以,,∵,,,,
所以,,又,,面,
所以面,又,所以面,
∵平面,所以面面,
由,在中易求得,又,所以,,
面面,面,所以面,
所以为与平面所成的角,
在中可求得,所以,
∴与面所成角的正弦值为.
22.【详解】(1)在中,由余弦定理,
即①,同理,在中,,即②,
①②得,所以当长度变化时,为定值,定值为1;
(2),为的内角,则
则由,可得,则、均为锐角
又,,则,
则,则
则
令,则
又在单调递增,,
可得,则的取值范围为,
则的取值范围为
同课章节目录
