鲁教版初一数学上册第三单元第7节探索与表达规律(含答案)
文档属性
| 名称 | 鲁教版初一数学上册第三单元第7节探索与表达规律(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 151.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-07 07:50:23 | ||
图片预览


文档简介
鲁教版初一数学上册第三单元第7节探索与表达规律
一.选择题(共8小题)
1.(2014 十堰)根据如图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
A.B. C.D.
2.(2014 涉县一模)将从1开始的正整数按如图方式排列.字母P,Q,M.N表示数字的位置,则2013这个数应排的位置是( )
A.P B. N C. Q D. M
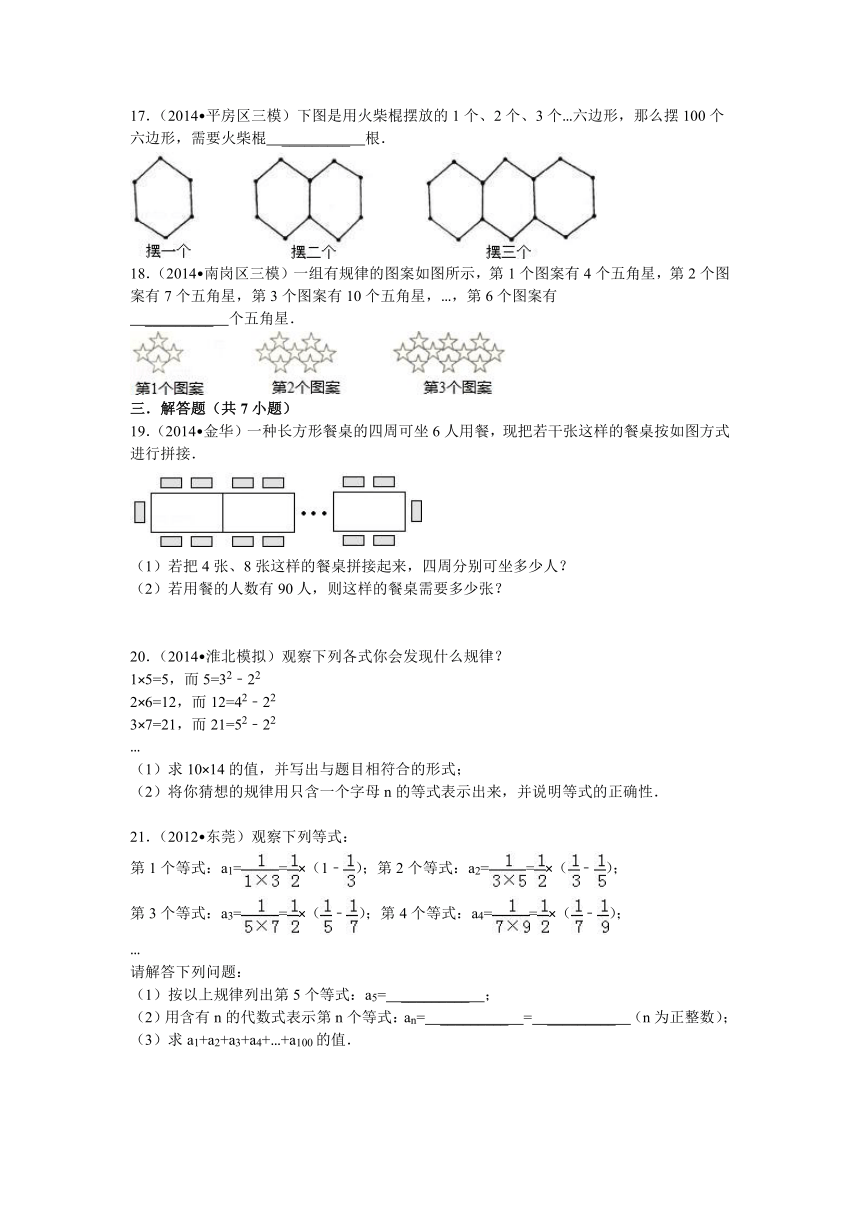
3.(2014 凤阳县模拟)观察下列图形:
它们是按一定规律排列的,依照此规律,第20个图形共有★个( )
A.63 B. 57 C. 68 D. 60
4.(2014 沙坪坝区一模)用若干张大小相同的黑白两种颜色的正方形纸片,按下列拼图的规律拼成一列图案,则第6个图案中黑色正方形纸片的张数是( )
A.22 B. 21 C. 20 D. 19
5.(2014 沙坪坝区二模)观察下列图形,则第7个图形中三角形的个数是( )
A.10 B. 28 C. 24 D. 32
6.(2014 十堰)观察下列图形的构成规律,按此规律,第10个图形中棋子的个数为( )
A.51 B. 45 C. 42 D. 31
7.(2013 南平)给定一列按规律排列的数:,则这列数的第6个数是( )
A. B. C. D.
8.(2013 日照)如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是( )
A.M=mn B. M=n(m+1) C. M=mn+1 D. M=m(n+1)
二.填空题(共10小题)
9.(2014 桂林)观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 _________ .
10.(2014 白银)观察下列各式:
13=12 13+23=32 13+23+33=62 13+23+33+43=102 …
猜想13+23+33+…+103= _________ .
11.(2014 毕节地区)观察下列一组数:,,,,,…,它们是按一定规律排列的,那么这一组数的第n个数是 _________ .
12.(2014 呼伦贝尔)一组等式:12+22+22=32,22+32+62=72,32+42+122=132,42+52+202=212…请观察它们的构成规律,用你发现的规律写出第9个等式 _________ .
13.(2014 雅安)已知:一组数1,3,5,7,9,…,按此规律,则第n个数是 ____ .
14.(2014 牡丹江)如图,是由一些点组成的图形,按此规律,在第n个图形中,点的个数为 _________ .
15.(2014 娄底)如图是一组有规律的图案,第1个图案由4个▲组成,第2个图案由7个▲组成,第3个图案由10个▲组成,第4个图案由13个▲组成,…,则第n(n为正整数)个图案由 _________ 个▲组成.
16.(2014 内江)如图,将若干个正三角形、正方形和圆按一定规律从左向右排列,那么第2014个图形是 _________ .
17.(2014 平房区三模)下图是用火柴棍摆放的1个、2个、3个…六边形,那么摆100个六边形,需要火柴棍 _________ 根.
18.(2014 南岗区三模)一组有规律的图案如图所示,第1个图案有4个五角星,第2个图案有7个五角星,第3个图案有10个五角星,…,第6个图案有
_________ 个五角星.
三.解答题(共7小题)
19.(2014 金华)一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
20.(2014 淮北模拟)观察下列各式你会发现什么规律?
1×5=5,而5=32﹣22
2×6=12,而12=42﹣22
3×7=21,而21=52﹣22
…
(1)求10×14的值,并写出与题目相符合的形式;
(2)将你猜想的规律用只含一个字母n的等式表示出来,并说明等式的正确性.
21.(2012 东莞)观察下列等式:
第1个等式:a1==×(1﹣);第2个等式:a2==×(﹣);
第3个等式:a3==×(﹣);第4个等式:a4==×(﹣);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= _________ ;
(2)用含有n的代数式表示第n个等式:an= _________ = _________ (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
22.(2012 珠海)观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× _________ = _________ ×25;
② _________ ×396=693× _________ .
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.
23.(2012 宁波)用同样大小的黑色棋子按如图所示的规律摆放:
(1)第5个图形有多少黑色棋子?
(2)第几个图形有2013颗黑色棋子?请说明理由.
24.(2012 锦州二模)观察下列等式:15×15=1×2×100+25=225,25×25=2×3×100+25=625,35×35=3×4×100+25=1225…,用自然数n(其中n≥1)表示上面一系列等式所反映出来的规律是 _________ .
25.(2010 济宁)观察下面的变形规律:=1﹣;=﹣;=﹣;…
解答下面的问题:
(1)若n为正整数,请你猜想= _________ ;
(2)证明你猜想的结论;
(3)求和:+++…+.
参考答案
一.选择题(共8小题)
1.D.2.B.3.D.4.D.5.B.6.D.7.A.8.D.
二.填空题(共10小题)
9. 2 .10. 552 .11. .12. 92+102+902=912 .
13. 2n﹣1 .14. n2+2 .15. 3n+1 16. □ .17. 501 18. 19
三.解答题(共7小题)
19.解:(1)1张长方形餐桌的四周可坐4+2=6人,
2张长方形餐桌的四周可坐4×2+2=10人,
3张长方形餐桌的四周可坐4×3+2=14人,
…
n张长方形餐桌的四周可坐4n+2人;
所以4张长方形餐桌的四周可坐4×4+2=18人,
8张长方形餐桌的四周可坐4×8+2=34人;
(2)设这样的餐桌需要x张,由题意得
4x+2=90
解得x=22
答:这样的餐桌需要22张.
20.解:(1)10×14=140=122﹣22;
(2)第n个等式为n(n+4)=(n+2)2﹣22.
∵左边=n(n+4)=n2+4n
右边=(n+2)2﹣22=n2+4n+4﹣4═n2+4n
左边=右边
∴n(n+4)=(n+2)2﹣22.
21.解:根据观察知答案分别为:
(1); ;
(2); ;
(3)a1+a2+a3+a4+…+a100
=×(1﹣)+×(﹣)+×(﹣)+×(﹣)+…+×
=(1﹣+﹣+﹣+﹣+…+﹣)
=(1﹣)
=×
=.
22.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× 275 = 572 ×25;
② 63 ×396=693× 36 .
证明:左边=(10a+b)×[100b+10(a+b)+a],
=(10a+b)(100b+10a+10b+a),
=(10a+b)(110b+11a),
=11(10a+b)(10b+a),
右边=[100a+10(a+b)+b]×(10b+a),
=(100a+10a+10b+b)(10b+a),
=(110a+11b)(10b+a),
=11(10a+b)(10b+a),
左边=右边,
23.解:(1)第一个图需棋子6,
第二个图需棋子9,
第三个图需棋子12,
第四个图需棋子15,
第五个图需棋子18,
…
第n个图需棋子3(n+1)枚.
答:第5个图形有18颗黑色棋子.
(2)设第n个图形有2013颗黑色棋子,
根据(1)得3(n+1)=2013
解得n=670,
所以第670个图形有2013颗黑色棋子.
24.解:∵15×15=1×2×100+25=225,
25×25=2×3×100+25=625,
35×35=3×4×100+25=1225,
…,
∴(10n+5)×(10n+5)=100n(n+1)+25.
故答案为:(10n+5)×(10n+5)=100n(n+1)+25.
25.(1)解:;
(2)证明:右边=﹣=﹣===左边,
所以猜想成立.
(3)原式=1﹣+﹣+﹣+…+﹣
=1﹣
=.
一.选择题(共8小题)
1.(2014 十堰)根据如图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
A.B. C.D.
2.(2014 涉县一模)将从1开始的正整数按如图方式排列.字母P,Q,M.N表示数字的位置,则2013这个数应排的位置是( )
A.P B. N C. Q D. M
3.(2014 凤阳县模拟)观察下列图形:
它们是按一定规律排列的,依照此规律,第20个图形共有★个( )
A.63 B. 57 C. 68 D. 60
4.(2014 沙坪坝区一模)用若干张大小相同的黑白两种颜色的正方形纸片,按下列拼图的规律拼成一列图案,则第6个图案中黑色正方形纸片的张数是( )
A.22 B. 21 C. 20 D. 19
5.(2014 沙坪坝区二模)观察下列图形,则第7个图形中三角形的个数是( )
A.10 B. 28 C. 24 D. 32
6.(2014 十堰)观察下列图形的构成规律,按此规律,第10个图形中棋子的个数为( )
A.51 B. 45 C. 42 D. 31
7.(2013 南平)给定一列按规律排列的数:,则这列数的第6个数是( )
A. B. C. D.
8.(2013 日照)如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是( )
A.M=mn B. M=n(m+1) C. M=mn+1 D. M=m(n+1)
二.填空题(共10小题)
9.(2014 桂林)观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 _________ .
10.(2014 白银)观察下列各式:
13=12 13+23=32 13+23+33=62 13+23+33+43=102 …
猜想13+23+33+…+103= _________ .
11.(2014 毕节地区)观察下列一组数:,,,,,…,它们是按一定规律排列的,那么这一组数的第n个数是 _________ .
12.(2014 呼伦贝尔)一组等式:12+22+22=32,22+32+62=72,32+42+122=132,42+52+202=212…请观察它们的构成规律,用你发现的规律写出第9个等式 _________ .
13.(2014 雅安)已知:一组数1,3,5,7,9,…,按此规律,则第n个数是 ____ .
14.(2014 牡丹江)如图,是由一些点组成的图形,按此规律,在第n个图形中,点的个数为 _________ .
15.(2014 娄底)如图是一组有规律的图案,第1个图案由4个▲组成,第2个图案由7个▲组成,第3个图案由10个▲组成,第4个图案由13个▲组成,…,则第n(n为正整数)个图案由 _________ 个▲组成.
16.(2014 内江)如图,将若干个正三角形、正方形和圆按一定规律从左向右排列,那么第2014个图形是 _________ .
17.(2014 平房区三模)下图是用火柴棍摆放的1个、2个、3个…六边形,那么摆100个六边形,需要火柴棍 _________ 根.
18.(2014 南岗区三模)一组有规律的图案如图所示,第1个图案有4个五角星,第2个图案有7个五角星,第3个图案有10个五角星,…,第6个图案有
_________ 个五角星.
三.解答题(共7小题)
19.(2014 金华)一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
20.(2014 淮北模拟)观察下列各式你会发现什么规律?
1×5=5,而5=32﹣22
2×6=12,而12=42﹣22
3×7=21,而21=52﹣22
…
(1)求10×14的值,并写出与题目相符合的形式;
(2)将你猜想的规律用只含一个字母n的等式表示出来,并说明等式的正确性.
21.(2012 东莞)观察下列等式:
第1个等式:a1==×(1﹣);第2个等式:a2==×(﹣);
第3个等式:a3==×(﹣);第4个等式:a4==×(﹣);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= _________ ;
(2)用含有n的代数式表示第n个等式:an= _________ = _________ (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
22.(2012 珠海)观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× _________ = _________ ×25;
② _________ ×396=693× _________ .
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.
23.(2012 宁波)用同样大小的黑色棋子按如图所示的规律摆放:
(1)第5个图形有多少黑色棋子?
(2)第几个图形有2013颗黑色棋子?请说明理由.
24.(2012 锦州二模)观察下列等式:15×15=1×2×100+25=225,25×25=2×3×100+25=625,35×35=3×4×100+25=1225…,用自然数n(其中n≥1)表示上面一系列等式所反映出来的规律是 _________ .
25.(2010 济宁)观察下面的变形规律:=1﹣;=﹣;=﹣;…
解答下面的问题:
(1)若n为正整数,请你猜想= _________ ;
(2)证明你猜想的结论;
(3)求和:+++…+.
参考答案
一.选择题(共8小题)
1.D.2.B.3.D.4.D.5.B.6.D.7.A.8.D.
二.填空题(共10小题)
9. 2 .10. 552 .11. .12. 92+102+902=912 .
13. 2n﹣1 .14. n2+2 .15. 3n+1 16. □ .17. 501 18. 19
三.解答题(共7小题)
19.解:(1)1张长方形餐桌的四周可坐4+2=6人,
2张长方形餐桌的四周可坐4×2+2=10人,
3张长方形餐桌的四周可坐4×3+2=14人,
…
n张长方形餐桌的四周可坐4n+2人;
所以4张长方形餐桌的四周可坐4×4+2=18人,
8张长方形餐桌的四周可坐4×8+2=34人;
(2)设这样的餐桌需要x张,由题意得
4x+2=90
解得x=22
答:这样的餐桌需要22张.
20.解:(1)10×14=140=122﹣22;
(2)第n个等式为n(n+4)=(n+2)2﹣22.
∵左边=n(n+4)=n2+4n
右边=(n+2)2﹣22=n2+4n+4﹣4═n2+4n
左边=右边
∴n(n+4)=(n+2)2﹣22.
21.解:根据观察知答案分别为:
(1); ;
(2); ;
(3)a1+a2+a3+a4+…+a100
=×(1﹣)+×(﹣)+×(﹣)+×(﹣)+…+×
=(1﹣+﹣+﹣+﹣+…+﹣)
=(1﹣)
=×
=.
22.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× 275 = 572 ×25;
② 63 ×396=693× 36 .
证明:左边=(10a+b)×[100b+10(a+b)+a],
=(10a+b)(100b+10a+10b+a),
=(10a+b)(110b+11a),
=11(10a+b)(10b+a),
右边=[100a+10(a+b)+b]×(10b+a),
=(100a+10a+10b+b)(10b+a),
=(110a+11b)(10b+a),
=11(10a+b)(10b+a),
左边=右边,
23.解:(1)第一个图需棋子6,
第二个图需棋子9,
第三个图需棋子12,
第四个图需棋子15,
第五个图需棋子18,
…
第n个图需棋子3(n+1)枚.
答:第5个图形有18颗黑色棋子.
(2)设第n个图形有2013颗黑色棋子,
根据(1)得3(n+1)=2013
解得n=670,
所以第670个图形有2013颗黑色棋子.
24.解:∵15×15=1×2×100+25=225,
25×25=2×3×100+25=625,
35×35=3×4×100+25=1225,
…,
∴(10n+5)×(10n+5)=100n(n+1)+25.
故答案为:(10n+5)×(10n+5)=100n(n+1)+25.
25.(1)解:;
(2)证明:右边=﹣=﹣===左边,
所以猜想成立.
(3)原式=1﹣+﹣+﹣+…+﹣
=1﹣
=.
