鲁教版初二第二章 轴对称复习练习题(含答案)
文档属性
| 名称 | 鲁教版初二第二章 轴对称复习练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-07 00:00:00 | ||
图片预览

文档简介
鲁教版初二第二单元复习练习题(含答案)
一.选择题(共10小题)
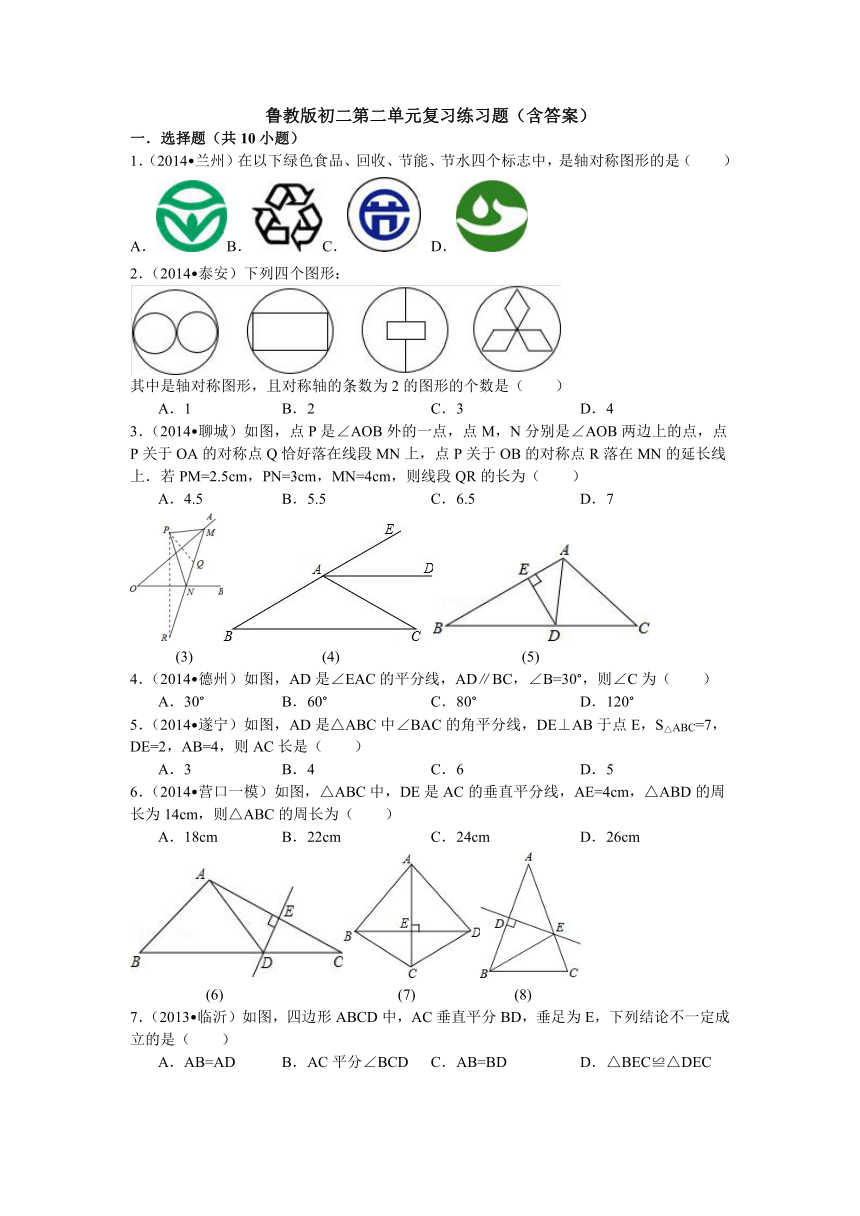
1.(2014 兰州)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.B.C. D.
2.(2014 泰安)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B. 2 C. 3 D. 4
3.(2014 聊城)如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
A.4.5 B. 5.5 C. 6.5 D. 7
(3) (4) (5)
4.(2014 德州)如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B. 60° C. 80° D. 120°
5.(2014 遂宁)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.3 B. 4 C. 6 D. 5
6.(2014 营口一模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
A.18cm B. 22cm C. 24cm D. 26cm
(6) (7) (8)
7.(2013 临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD B. AC平分∠BCD C. AB=BD D. △BEC≌△DEC
8.(2014 丹东)如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为( )
A.70° B. 80° C. 40° D. 30°
9.(2014 黔西南州)已知等腰三角形△ABC中,腰AB=8,底BC=5,则这个三角形的周长为( )
A.21 B. 20 C. 19 D. 18
10.(2013 湖北)如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.4cm B. 3cm C. 2cm D. 1cm
(10) (11) (12)
二.填空题(共8小题)
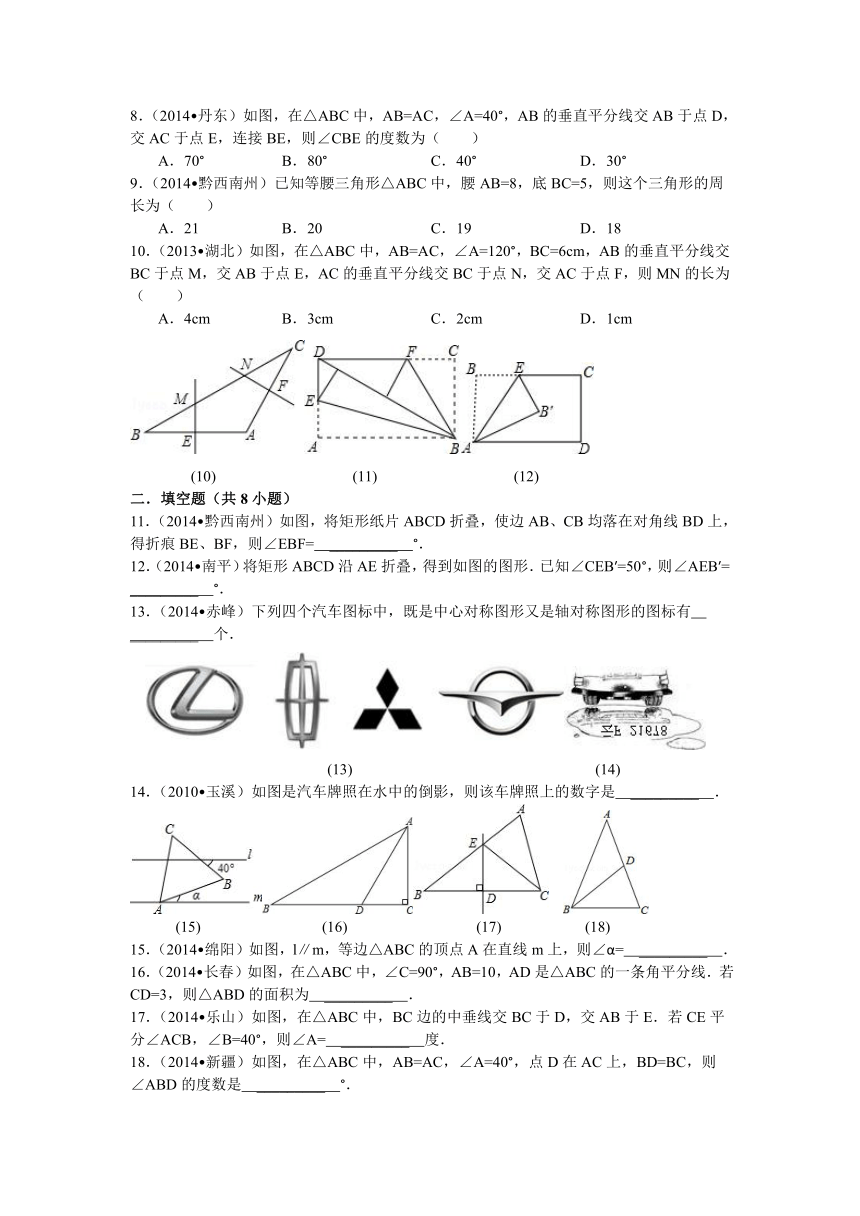
11.(2014 黔西南州)如图,将矩形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF= _________ °.
12.(2014 南平)将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=50°,则∠AEB′= _________ °.
13.(2014 赤峰)下列四个汽车图标中,既是中心对称图形又是轴对称图形的图标有 _________ 个.
(13) (14)
14.(2010 玉溪)如图是汽车牌照在水中的倒影,则该车牌照上的数字是 _________ .
(15) (16) (17) (18)
15.(2014 绵阳)如图,l∥m,等边△ABC的顶点A在直线m上,则∠α= _________ .
16.(2014 长春)如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为 _________ .
17.(2014 乐山)如图,在△ABC中,BC边的中垂线交BC于D,交AB于E.若CE平分∠ACB,∠B=40°,则∠A= _________ 度.
18.(2014 新疆)如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,则∠ABD的度数是 _________ °.
三.解答题(共4小题)
19.(2014 黄冈)已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
20.(2014 龙岩)如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.
(1)求证:CE=BF;
(2)求∠BPC的度数.
21.(2014 杭州)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.
22.(2014 白银)如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
参考答案
一.选择题(共10小题)
1.A.2.C.3. A.4.A.5.A.6.B.7.C.8.D.9.A.10.C.
二.填空题(共8小题)
11. 45 °.12. 65 °.13. 1 14. 21678 15. 20° .
16. 15 .17. 60 度18. 30 °.
三.解答题(共4小题)
19.证明:连接AD,
在△ACD和△ABD中,
,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
20.(1)证明:如图,∵△ABC是等边三角形,
∴BC=AB,∠A=∠EBC=60°,
∴在△BCE与△ABF中,
,
∴△BCE≌△ABF(SAS),
∴CE=BF;
(2)解:∵由(1)知△BCE≌△ABF,
∴∠BCE=∠ABF,
∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,
∴∠BPC=180°﹣60°=120°.
即:∠BPC=120°.
21.解:在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE(全等三角形的对应角相等),
∴BF=CE(全等三角形的对应边相等),
∵AB=AC,AE=AF,
∴BE=CF,
在△BEP和△CFP中,
,
∴△BEP≌△CFP(AAS),
∴PB=PC,
∵BF=CE,
∴PE=PF,
∴图中相等的线段为PE=PF,BE=CF,BF=CE.
22.(1)解:如图所示,DE就是要求作的AB边上的中垂线;
(2)证明:∵DE是AB边上的中垂线,∠A=30°,
∴AD=BD,
∴∠ABD=∠A=30°,
∵∠C=90°,
∴∠ABC=90°﹣∠A=90°﹣30°=60°,
∴∠CBD=∠ABC﹣∠ABD=60°﹣30°=30°,
∴∠ABD=∠CBD,
∴BD平分∠CBA.
一.选择题(共10小题)
1.(2014 兰州)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.B.C. D.
2.(2014 泰安)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B. 2 C. 3 D. 4
3.(2014 聊城)如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
A.4.5 B. 5.5 C. 6.5 D. 7
(3) (4) (5)
4.(2014 德州)如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B. 60° C. 80° D. 120°
5.(2014 遂宁)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.3 B. 4 C. 6 D. 5
6.(2014 营口一模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
A.18cm B. 22cm C. 24cm D. 26cm
(6) (7) (8)
7.(2013 临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD B. AC平分∠BCD C. AB=BD D. △BEC≌△DEC
8.(2014 丹东)如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为( )
A.70° B. 80° C. 40° D. 30°
9.(2014 黔西南州)已知等腰三角形△ABC中,腰AB=8,底BC=5,则这个三角形的周长为( )
A.21 B. 20 C. 19 D. 18
10.(2013 湖北)如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.4cm B. 3cm C. 2cm D. 1cm
(10) (11) (12)
二.填空题(共8小题)
11.(2014 黔西南州)如图,将矩形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF= _________ °.
12.(2014 南平)将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=50°,则∠AEB′= _________ °.
13.(2014 赤峰)下列四个汽车图标中,既是中心对称图形又是轴对称图形的图标有 _________ 个.
(13) (14)
14.(2010 玉溪)如图是汽车牌照在水中的倒影,则该车牌照上的数字是 _________ .
(15) (16) (17) (18)
15.(2014 绵阳)如图,l∥m,等边△ABC的顶点A在直线m上,则∠α= _________ .
16.(2014 长春)如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为 _________ .
17.(2014 乐山)如图,在△ABC中,BC边的中垂线交BC于D,交AB于E.若CE平分∠ACB,∠B=40°,则∠A= _________ 度.
18.(2014 新疆)如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,则∠ABD的度数是 _________ °.
三.解答题(共4小题)
19.(2014 黄冈)已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
20.(2014 龙岩)如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.
(1)求证:CE=BF;
(2)求∠BPC的度数.
21.(2014 杭州)在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.
22.(2014 白银)如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
参考答案
一.选择题(共10小题)
1.A.2.C.3. A.4.A.5.A.6.B.7.C.8.D.9.A.10.C.
二.填空题(共8小题)
11. 45 °.12. 65 °.13. 1 14. 21678 15. 20° .
16. 15 .17. 60 度18. 30 °.
三.解答题(共4小题)
19.证明:连接AD,
在△ACD和△ABD中,
,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
20.(1)证明:如图,∵△ABC是等边三角形,
∴BC=AB,∠A=∠EBC=60°,
∴在△BCE与△ABF中,
,
∴△BCE≌△ABF(SAS),
∴CE=BF;
(2)解:∵由(1)知△BCE≌△ABF,
∴∠BCE=∠ABF,
∴∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60°,即∠PBC+∠PCB=60°,
∴∠BPC=180°﹣60°=120°.
即:∠BPC=120°.
21.解:在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE(全等三角形的对应角相等),
∴BF=CE(全等三角形的对应边相等),
∵AB=AC,AE=AF,
∴BE=CF,
在△BEP和△CFP中,
,
∴△BEP≌△CFP(AAS),
∴PB=PC,
∵BF=CE,
∴PE=PF,
∴图中相等的线段为PE=PF,BE=CF,BF=CE.
22.(1)解:如图所示,DE就是要求作的AB边上的中垂线;
(2)证明:∵DE是AB边上的中垂线,∠A=30°,
∴AD=BD,
∴∠ABD=∠A=30°,
∵∠C=90°,
∴∠ABC=90°﹣∠A=90°﹣30°=60°,
∴∠CBD=∠ABC﹣∠ABD=60°﹣30°=30°,
∴∠ABD=∠CBD,
∴BD平分∠CBA.
