数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共14张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.1对数的概念 课件(共14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 368.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 20:01:33 | ||
图片预览




文档简介
(共14张PPT)
4.3.1 对数的概念
【设计问题,创设情境】
对数的概念,首先是由苏格兰数学家纳皮尔(J.Napier,1550~1617)提出的.那时候天文学是热门学科.可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间.纳皮尔也是一位天文爱好者,他感到,“没有什么会比数学的演算更加令人烦恼……诸如一些大数的乘、除、平方、立方、开方……因此我开始考虑……怎样才能排除这些障碍.”经过20年潜心研究大数的计算技术,他终于独立发明了对数,并于1614年出版的名著《奇妙的对数定律说明书》中阐明了对数原理,后人称为纳皮尔对数.
探究:对数主要作用是什么
提示:简化运算.
299 792.468×31 536 000=?
光速m/s
一年s
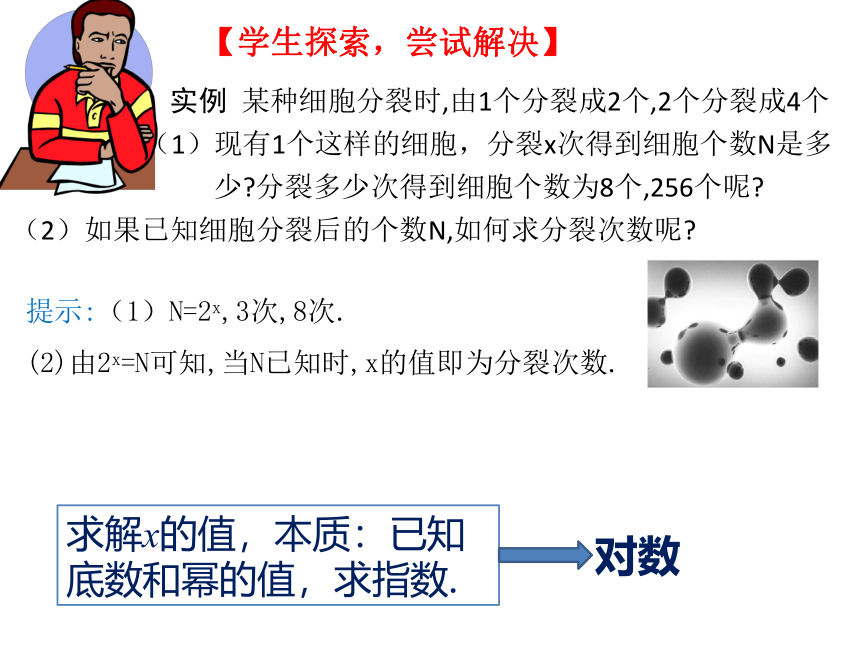
【学生探索,尝试解决】
实例 某种细胞分裂时,由1个分裂成2个,2个分裂成4个
(1)现有1个这样的细胞,分裂x次得到细胞个数N是多
少 分裂多少次得到细胞个数为8个,256个呢
(2)如果已知细胞分裂后的个数N,如何求分裂次数呢
提示:(1)N=2x,3次,8次.
(2)由2x=N可知,当N已知时,x的值即为分裂次数.
对数
求解x的值,本质:已知底数和幂的值,求指数.
【对数的概念】
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作
其中a叫做对数的底数,N叫做真数.
x=logaN,
对数的读法
对数的写法
对数的符号:
英国数学家约翰 纳皮尔创造了“Logarithm(对数)”一词,直至1624年,开普勒将其简化为“Log”,经过多次演编现在用“log”.
注意:1. 同 等符号一样,表示一种运算,只不过对数运算的符号写在数的前面,即已知底数a和它的幂N求指数的运算,这种运算叫对数运算,对数运算结果仍是一个实数.
2.
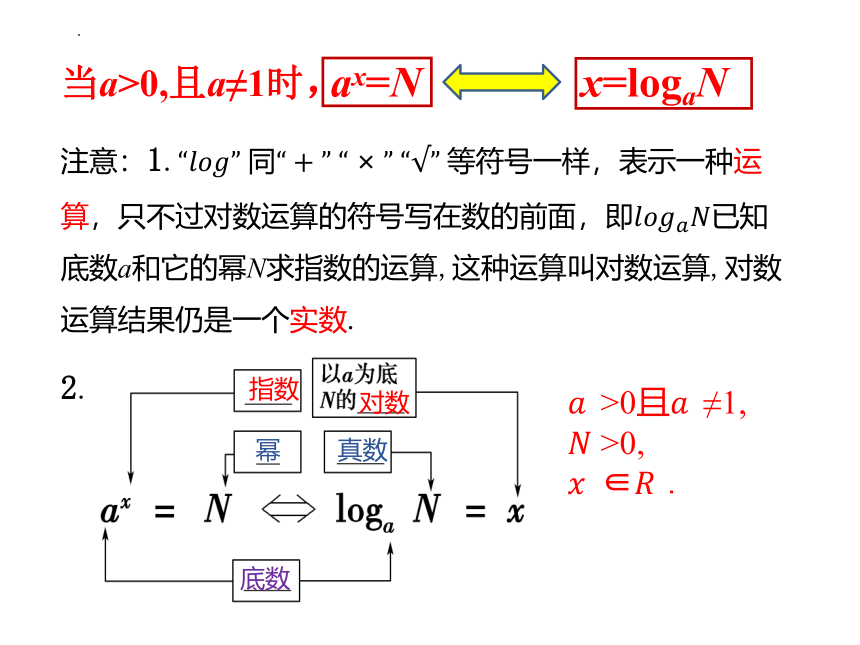
当a>0,且a≠1时,
ax=N
x=logaN
底数
指数
真数
幂
对数
>0且 ≠1, >0,
∈ .
【典例剖析】
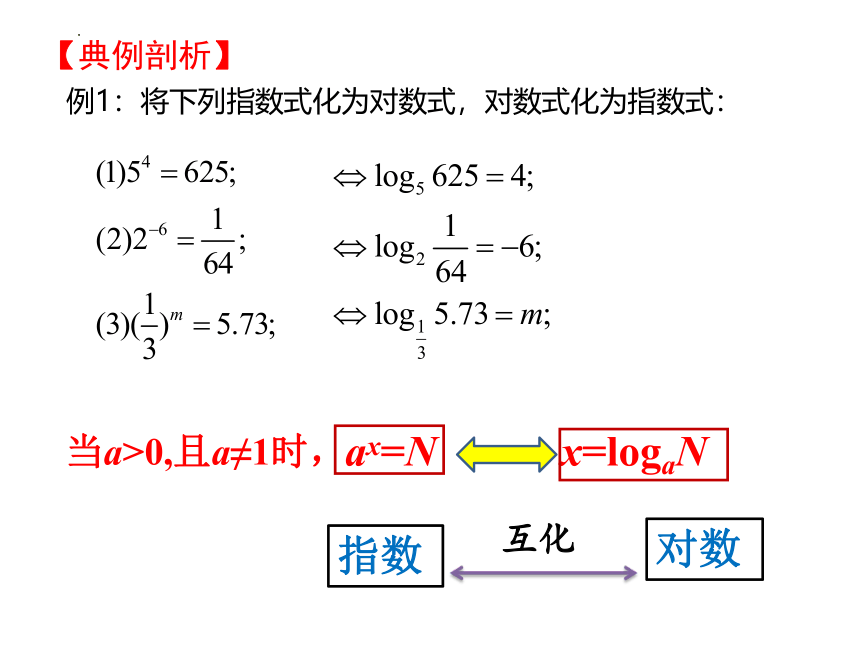
指数
对数
互化
当a>0,且a≠1时,
ax=N
x=logaN
例1:将下列指数式化为对数式,对数式化为指数式:
【典例剖析】
指数
对数
互化
当a>0,且a≠1时,
ax=N
x=logaN
例1:将下列指数式化为对数式,对数式化为指数式:
【常用对数】
1.通常,我们将以10为底的对数叫做常用对数,
并把 记为 .
2.通常,以无理数e=2.71828…为底数的对数,称为自然对数,并把 记为 .
log10N记为lgN,
logeN记为lnN.
【对数的重要结论】
(1)负数和零没有对数.
=N, N>0.
当真数N时, 没有对数.
=N, .
令,则.
【对数的重要结论】
=N, .
令,则.
(5)
,
即时训练1:求下列各式中x的值.
(1)lg(ln x)=1;
(2)lg(ln x)=0.
解:(1)由lg(ln x)=1得ln x=10,所以x=e10.
(2)由lg(ln x)=0得ln x=1,
所以x=e.
练习2 口答下列各式的值:
(1)log525=
(2)log0.21=
(3)lne=
(4)lg0.01=
变式:
(1)loga1=______;
(2)logaa=______.
【变练演编,深化提高】
对数的概念:
x=logaN
指数
ax=N
指数函数的性质
转化与化归思想
函数与方程思想
对数的运算?
相互转化
【反思小结,观点提炼】
1.对数的概念,指数式与对数式的转化;
2.对数的相关结论及运用;
3.对数发明的背景与原理.
4.3.1 对数的概念
【设计问题,创设情境】
对数的概念,首先是由苏格兰数学家纳皮尔(J.Napier,1550~1617)提出的.那时候天文学是热门学科.可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间.纳皮尔也是一位天文爱好者,他感到,“没有什么会比数学的演算更加令人烦恼……诸如一些大数的乘、除、平方、立方、开方……因此我开始考虑……怎样才能排除这些障碍.”经过20年潜心研究大数的计算技术,他终于独立发明了对数,并于1614年出版的名著《奇妙的对数定律说明书》中阐明了对数原理,后人称为纳皮尔对数.
探究:对数主要作用是什么
提示:简化运算.
299 792.468×31 536 000=?
光速m/s
一年s
【学生探索,尝试解决】
实例 某种细胞分裂时,由1个分裂成2个,2个分裂成4个
(1)现有1个这样的细胞,分裂x次得到细胞个数N是多
少 分裂多少次得到细胞个数为8个,256个呢
(2)如果已知细胞分裂后的个数N,如何求分裂次数呢
提示:(1)N=2x,3次,8次.
(2)由2x=N可知,当N已知时,x的值即为分裂次数.
对数
求解x的值,本质:已知底数和幂的值,求指数.
【对数的概念】
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作
其中a叫做对数的底数,N叫做真数.
x=logaN,
对数的读法
对数的写法
对数的符号:
英国数学家约翰 纳皮尔创造了“Logarithm(对数)”一词,直至1624年,开普勒将其简化为“Log”,经过多次演编现在用“log”.
注意:1. 同 等符号一样,表示一种运算,只不过对数运算的符号写在数的前面,即已知底数a和它的幂N求指数的运算,这种运算叫对数运算,对数运算结果仍是一个实数.
2.
当a>0,且a≠1时,
ax=N
x=logaN
底数
指数
真数
幂
对数
>0且 ≠1, >0,
∈ .
【典例剖析】
指数
对数
互化
当a>0,且a≠1时,
ax=N
x=logaN
例1:将下列指数式化为对数式,对数式化为指数式:
【典例剖析】
指数
对数
互化
当a>0,且a≠1时,
ax=N
x=logaN
例1:将下列指数式化为对数式,对数式化为指数式:
【常用对数】
1.通常,我们将以10为底的对数叫做常用对数,
并把 记为 .
2.通常,以无理数e=2.71828…为底数的对数,称为自然对数,并把 记为 .
log10N记为lgN,
logeN记为lnN.
【对数的重要结论】
(1)负数和零没有对数.
=N, N>0.
当真数N时, 没有对数.
=N, .
令,则.
【对数的重要结论】
=N, .
令,则.
(5)
,
即时训练1:求下列各式中x的值.
(1)lg(ln x)=1;
(2)lg(ln x)=0.
解:(1)由lg(ln x)=1得ln x=10,所以x=e10.
(2)由lg(ln x)=0得ln x=1,
所以x=e.
练习2 口答下列各式的值:
(1)log525=
(2)log0.21=
(3)lne=
(4)lg0.01=
变式:
(1)loga1=______;
(2)logaa=______.
【变练演编,深化提高】
对数的概念:
x=logaN
指数
ax=N
指数函数的性质
转化与化归思想
函数与方程思想
对数的运算?
相互转化
【反思小结,观点提炼】
1.对数的概念,指数式与对数式的转化;
2.对数的相关结论及运用;
3.对数发明的背景与原理.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
