2.1 两条直线的位置关系第1课时 教学设计(表格式)北师大版数学七年级下册
文档属性
| 名称 | 2.1 两条直线的位置关系第1课时 教学设计(表格式)北师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 00:00:00 | ||
图片预览


文档简介
第二章 相交线与平行线
1 两条直线的位置关系
第1课时
一、 教学目标
1. 了解两条直线的相交和平行关系.
2. 理解对顶角、补角、余角等概念,掌握对顶角相等、等角的余角相等、等角的补角相等,并能解决一此实际问题.
3. 经历观察、操作、推理、交流等过程,进一步发展空间观念、推理能力和初步的有条理表达的能力.
4.激发学生学习数学的兴趣,认识到现实生活中蕴含着大量的数量和图形的有关问题,这些问题可以抽象成数学问题,用数学方法予以解决.
二、 教学重难点
重点:了解两条直线的相交和平行关系.
难点:理解对顶角、补角、余角等概念,掌握对顶角相等、等角的余角相等、等角的补角相等,并能解决一此实际问题.
三、教学用具
电脑、多媒体、课件等.
四、教学过程设计
教学环节 教师活动 学生活动 设计意图
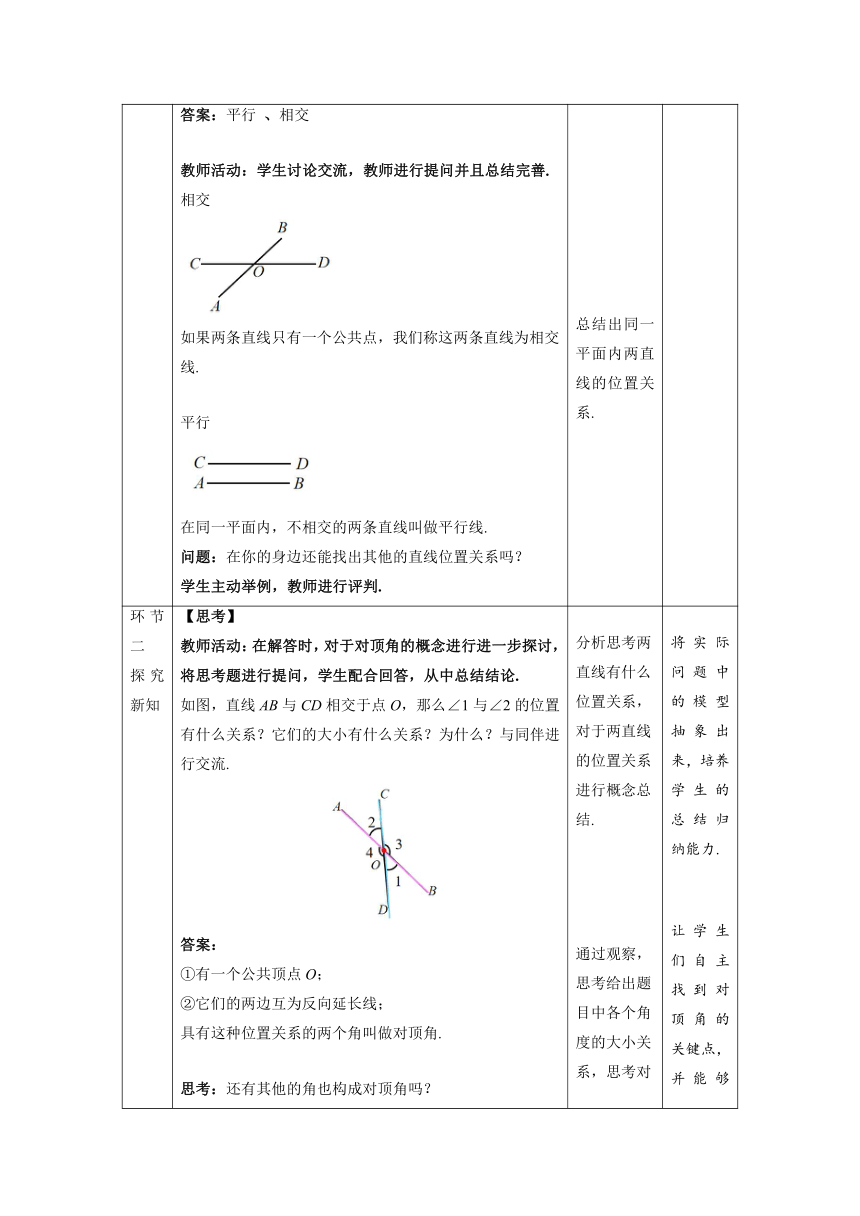
环节一 创设情境 【情境引入】 教师活动:教师展示下列图片,学生快速回答.让学生在列举一些生活中两直线的位置关系的实例. 观察下面几幅生活中的图片: 思考:在同一平面内,两条直线的位置关系有几种? 答案:平行 、相交 教师活动:学生讨论交流,教师进行提问并且总结完善. 相交 如果两条直线只有一个公共点,我们称这两条直线为相交线. 平行 在同一平面内,不相交的两条直线叫做平行线. 问题:在你的身边还能找出其他的直线位置关系吗? 学生主动举例,教师进行评判. 将图片中直线提取出来,并且思考图形中直线的位置关系. 总结出同一平面内两直线的位置关系. 通过与学生已有的生活经验联系,在情景中了解两条直线的相交和平行关系.
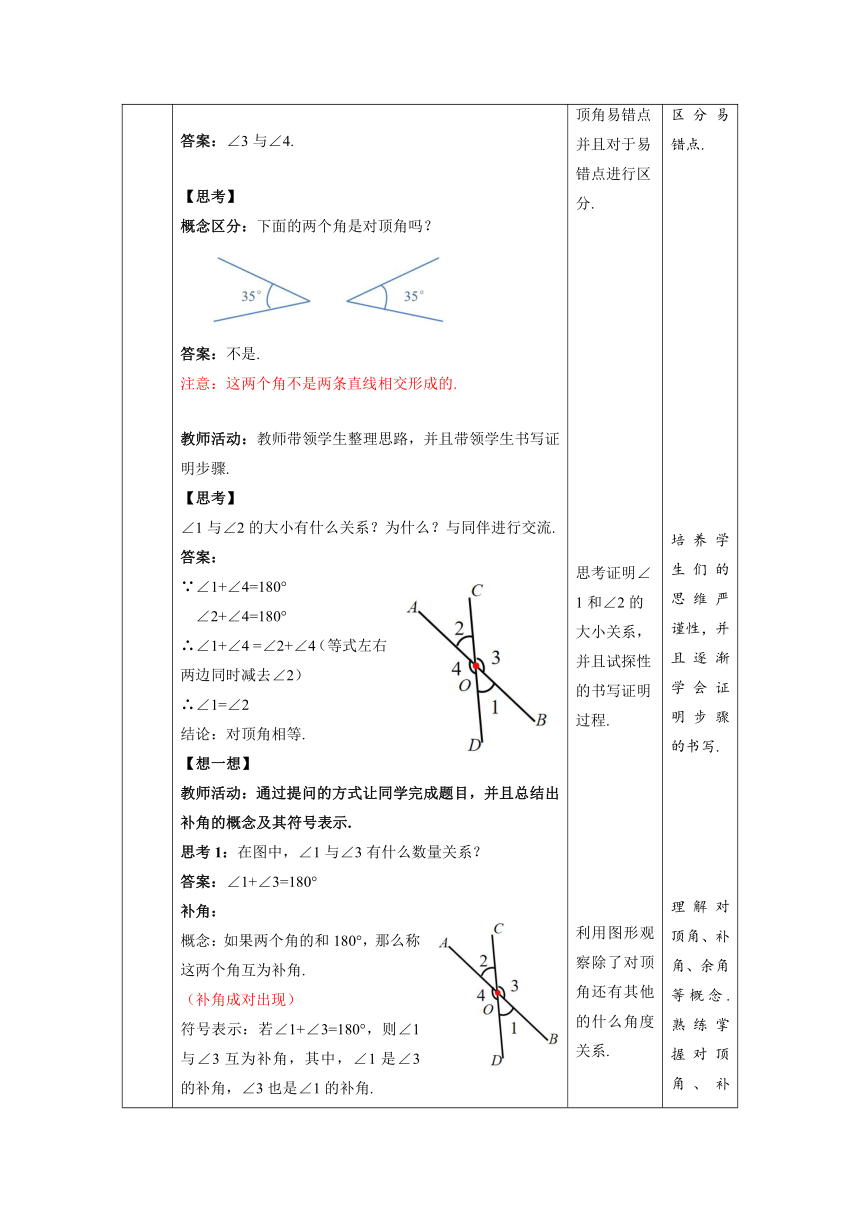
环节二 探究新知 【思考】 教师活动:在解答时,对于对顶角的概念进行进一步探讨,将思考题进行提问,学生配合回答,从中总结结论. 如图,直线AB与CD相交于点O,那么∠1与∠2的位置有什么关系?它们的大小有什么关系?为什么?与同伴进行交流. 答案: ①有一个公共顶点O; ②它们的两边互为反向延长线; 具有这种位置关系的两个角叫做对顶角. 思考:还有其他的角也构成对顶角吗? 答案:∠3与∠4. 【思考】 概念区分:下面的两个角是对顶角吗? 答案:不是. 注意:这两个角不是两条直线相交形成的. 教师活动:教师带领学生整理思路,并且带领学生书写证明步骤. 【思考】 ∠1与∠2的大小有什么关系?为什么?与同伴进行交流. 答案: ∵∠1+∠4=180° ∠2+∠4=180° ∴∠1+∠4 =∠2+∠4(等式左右两边同时减去∠2) ∴∠1=∠2 结论:对顶角相等. 【想一想】 教师活动:通过提问的方式让同学完成题目,并且总结出补角的概念及其符号表示. 思考1:在图中,∠1与∠3有什么数量关系? 答案:∠1+∠3=180° 补角: 概念:如果两个角的和180°,那么称这两个角互为补角. (补角成对出现) 符号表示:若∠1+∠3=180°,则∠1与∠3互为补角,其中,∠1是∠3的补角,∠3也是∠1的补角. 思考2:在图中,还有其他的角也构成互为补角的关系吗? 答案:∠2+∠4=180°→∠2与∠4互为补角 ∠1+∠4=180°→∠1与∠4互为补角 ∠2+∠3=180°→∠2与∠3互为补角 【探究】 教师活动:通过提问的方式让同学完成题目,并且总结出余角的概念. 思考1:在图中,∠5与∠6有什么关系? 答案:∠5+∠6=90° 余角: 概念:如果两个角的和是90°,那么称这两个角互为余角.(余角成对出现) 符号表示:若∠5+∠6=90°,则∠5与∠6互为余角,其中,∠5是∠6的余角,∠6也是∠5的余角. 【做一做】 教师活动:教师通过提问的方式,先带领同学理解将实际问题抽象成为几何关系,让同学们根据简化的几何关系找到解决问题的思路,之后补充解答过程,最后由教师完善解题步骤. 如图,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2. 将图1简化为图2,ON与DC相交所成的∠DON和∠CON都等于90°,且∠1=∠2.在图2中 有哪些角互为补角?有哪些角互为余角? 答案:互为补角的角:两个角的度数和为180° ∠AOD与∠AOC, ∠DON与∠CON, ∠BOC与∠BOD; 互为余角的角:两个角的度数和为90° ∠1与∠3、∠2与∠4. ∠3与∠4有什么关系?为什么? 答案:∠3=∠4 证明:∵∠1=∠2, ∠DON=∠CON=90° ∴∠DON–∠1=∠CON–∠2 即∠3=∠4 思考:你从中能总结出什么结论? 答案:同角或等角的余角相等 (3)∠AOC与∠BOD有什么关系?为什么? 答案:∠AOC=∠BOD 证明:∵∠1=∠2 ∴∠1+∠AOB=∠2+∠AOB (这一步的证明也可以用补角计算180°–∠1=180°–∠2) 即∠AOC=∠BOD 思考:你从中能总结出什么结论? 答案:同角或等角的补角相等. 分析思考两直线有什么位置关系,对于两直线的位置关系进行概念总结. 通过观察,思考给出题目中各个角度的大小关系,思考对顶角易错点并且对于易错点进行区分. 思考证明∠1和∠2的大小关系,并且试探性的书写证明过程. 利用图形观察除了对顶角还有其他的什么角度关系. 观察图中互为补角的两个角的角度关系,学习互为补角的符号表示. 观察图中互为余角的两个角的角度关系,学习互为余角的符号表示. 学生自主学习、尝试独立解答,并交流讨论. 将实际问题中的模型抽象出来,培养学生的总结归纳能力. 让学生们自主找到对顶角的关键点,并能够区分易错点. 培养学生们的思维严谨性,并且逐渐学会证明步骤的书写. 理解对顶角、补角、余角等概念.熟练掌握对顶角、补角、余角等符号表示. 引导学生探索出“同角或等角的余角相等,同角或等角的补角相等”的结论.
环节三 应用新知 【典型例题】 教师活动:提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程. 如图,直线a、b相交,若∠1 = 40°,求 ∠2、∠3、∠4的度数. 答案: 解:由邻补角的定义可得, ∠1 = 40° ∠2 = 180°-∠1 = 180°- 40° = 140° 由对顶角相等,可得 ∠3 = ∠1 = 40° ∠4 = ∠2 = 140° 思考问题,尝试回答问题,明确例题的做法 通过例题的讲解,让学生掌握求角度之间的逻辑关系和证明的书写.培养学生的综合能力.
环节四 巩固新知 【随堂练习】 教师活动:教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数.你能说出所量角是多少度吗?你的根据是什么? 答案:方法不唯一 方法一:利用补角得出所量角的度数 ∠1=180°-∠2=180°-140°=40° 方法二:根据对顶角相等得出所量角的度数 ∠1=∠3=40° 2、如图所示,∠1和∠2是对顶角的是( ). 答案:D 注意:对顶角直接找相交的两条直线. 3、如图,在所标注的角中. (1)对顶角有( )对, 邻补角有( )对. (2)若∠2+∠3=70°,∠1=150°,求∠3和∠4的度数. 答案:解:(1)对顶角:∠5与∠7、∠6与∠8;共2对. 邻补角:∠1与∠2、∠3与∠4、∠5与∠6、 ∠7与∠8、∠5与∠8、∠6与∠7;共6对. (2)∵∠1与∠2是邻补角 ∴∠1+∠2=180° ∵∠1=150° ∴∠2=30° ∵∠2+∠3=70° ∴∠3=40° ∵∠3与∠4是邻补角 ∴∠4=180°– ∠3=140° 自主完成练习,然后集体交流评价. 及时巩固所学知识,了解学生的学习效果,增强学生应用知识的能力.
环节五 课堂小结 思维导图的形式呈现本节课的主要内容: 在教师的引导下,回顾反思本节课所掌握的知识、技能、思想方法. 培养学生总结知识的能力,巩固新知,形成本节课重点内容框架.
环节六 布置作业 教科书第40页习题2.1 第1、2、3题 学生课后自主完成. 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
1 两条直线的位置关系
第1课时
一、 教学目标
1. 了解两条直线的相交和平行关系.
2. 理解对顶角、补角、余角等概念,掌握对顶角相等、等角的余角相等、等角的补角相等,并能解决一此实际问题.
3. 经历观察、操作、推理、交流等过程,进一步发展空间观念、推理能力和初步的有条理表达的能力.
4.激发学生学习数学的兴趣,认识到现实生活中蕴含着大量的数量和图形的有关问题,这些问题可以抽象成数学问题,用数学方法予以解决.
二、 教学重难点
重点:了解两条直线的相交和平行关系.
难点:理解对顶角、补角、余角等概念,掌握对顶角相等、等角的余角相等、等角的补角相等,并能解决一此实际问题.
三、教学用具
电脑、多媒体、课件等.
四、教学过程设计
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 【情境引入】 教师活动:教师展示下列图片,学生快速回答.让学生在列举一些生活中两直线的位置关系的实例. 观察下面几幅生活中的图片: 思考:在同一平面内,两条直线的位置关系有几种? 答案:平行 、相交 教师活动:学生讨论交流,教师进行提问并且总结完善. 相交 如果两条直线只有一个公共点,我们称这两条直线为相交线. 平行 在同一平面内,不相交的两条直线叫做平行线. 问题:在你的身边还能找出其他的直线位置关系吗? 学生主动举例,教师进行评判. 将图片中直线提取出来,并且思考图形中直线的位置关系. 总结出同一平面内两直线的位置关系. 通过与学生已有的生活经验联系,在情景中了解两条直线的相交和平行关系.
环节二 探究新知 【思考】 教师活动:在解答时,对于对顶角的概念进行进一步探讨,将思考题进行提问,学生配合回答,从中总结结论. 如图,直线AB与CD相交于点O,那么∠1与∠2的位置有什么关系?它们的大小有什么关系?为什么?与同伴进行交流. 答案: ①有一个公共顶点O; ②它们的两边互为反向延长线; 具有这种位置关系的两个角叫做对顶角. 思考:还有其他的角也构成对顶角吗? 答案:∠3与∠4. 【思考】 概念区分:下面的两个角是对顶角吗? 答案:不是. 注意:这两个角不是两条直线相交形成的. 教师活动:教师带领学生整理思路,并且带领学生书写证明步骤. 【思考】 ∠1与∠2的大小有什么关系?为什么?与同伴进行交流. 答案: ∵∠1+∠4=180° ∠2+∠4=180° ∴∠1+∠4 =∠2+∠4(等式左右两边同时减去∠2) ∴∠1=∠2 结论:对顶角相等. 【想一想】 教师活动:通过提问的方式让同学完成题目,并且总结出补角的概念及其符号表示. 思考1:在图中,∠1与∠3有什么数量关系? 答案:∠1+∠3=180° 补角: 概念:如果两个角的和180°,那么称这两个角互为补角. (补角成对出现) 符号表示:若∠1+∠3=180°,则∠1与∠3互为补角,其中,∠1是∠3的补角,∠3也是∠1的补角. 思考2:在图中,还有其他的角也构成互为补角的关系吗? 答案:∠2+∠4=180°→∠2与∠4互为补角 ∠1+∠4=180°→∠1与∠4互为补角 ∠2+∠3=180°→∠2与∠3互为补角 【探究】 教师活动:通过提问的方式让同学完成题目,并且总结出余角的概念. 思考1:在图中,∠5与∠6有什么关系? 答案:∠5+∠6=90° 余角: 概念:如果两个角的和是90°,那么称这两个角互为余角.(余角成对出现) 符号表示:若∠5+∠6=90°,则∠5与∠6互为余角,其中,∠5是∠6的余角,∠6也是∠5的余角. 【做一做】 教师活动:教师通过提问的方式,先带领同学理解将实际问题抽象成为几何关系,让同学们根据简化的几何关系找到解决问题的思路,之后补充解答过程,最后由教师完善解题步骤. 如图,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2. 将图1简化为图2,ON与DC相交所成的∠DON和∠CON都等于90°,且∠1=∠2.在图2中 有哪些角互为补角?有哪些角互为余角? 答案:互为补角的角:两个角的度数和为180° ∠AOD与∠AOC, ∠DON与∠CON, ∠BOC与∠BOD; 互为余角的角:两个角的度数和为90° ∠1与∠3、∠2与∠4. ∠3与∠4有什么关系?为什么? 答案:∠3=∠4 证明:∵∠1=∠2, ∠DON=∠CON=90° ∴∠DON–∠1=∠CON–∠2 即∠3=∠4 思考:你从中能总结出什么结论? 答案:同角或等角的余角相等 (3)∠AOC与∠BOD有什么关系?为什么? 答案:∠AOC=∠BOD 证明:∵∠1=∠2 ∴∠1+∠AOB=∠2+∠AOB (这一步的证明也可以用补角计算180°–∠1=180°–∠2) 即∠AOC=∠BOD 思考:你从中能总结出什么结论? 答案:同角或等角的补角相等. 分析思考两直线有什么位置关系,对于两直线的位置关系进行概念总结. 通过观察,思考给出题目中各个角度的大小关系,思考对顶角易错点并且对于易错点进行区分. 思考证明∠1和∠2的大小关系,并且试探性的书写证明过程. 利用图形观察除了对顶角还有其他的什么角度关系. 观察图中互为补角的两个角的角度关系,学习互为补角的符号表示. 观察图中互为余角的两个角的角度关系,学习互为余角的符号表示. 学生自主学习、尝试独立解答,并交流讨论. 将实际问题中的模型抽象出来,培养学生的总结归纳能力. 让学生们自主找到对顶角的关键点,并能够区分易错点. 培养学生们的思维严谨性,并且逐渐学会证明步骤的书写. 理解对顶角、补角、余角等概念.熟练掌握对顶角、补角、余角等符号表示. 引导学生探索出“同角或等角的余角相等,同角或等角的补角相等”的结论.
环节三 应用新知 【典型例题】 教师活动:提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程. 如图,直线a、b相交,若∠1 = 40°,求 ∠2、∠3、∠4的度数. 答案: 解:由邻补角的定义可得, ∠1 = 40° ∠2 = 180°-∠1 = 180°- 40° = 140° 由对顶角相等,可得 ∠3 = ∠1 = 40° ∠4 = ∠2 = 140° 思考问题,尝试回答问题,明确例题的做法 通过例题的讲解,让学生掌握求角度之间的逻辑关系和证明的书写.培养学生的综合能力.
环节四 巩固新知 【随堂练习】 教师活动:教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数.你能说出所量角是多少度吗?你的根据是什么? 答案:方法不唯一 方法一:利用补角得出所量角的度数 ∠1=180°-∠2=180°-140°=40° 方法二:根据对顶角相等得出所量角的度数 ∠1=∠3=40° 2、如图所示,∠1和∠2是对顶角的是( ). 答案:D 注意:对顶角直接找相交的两条直线. 3、如图,在所标注的角中. (1)对顶角有( )对, 邻补角有( )对. (2)若∠2+∠3=70°,∠1=150°,求∠3和∠4的度数. 答案:解:(1)对顶角:∠5与∠7、∠6与∠8;共2对. 邻补角:∠1与∠2、∠3与∠4、∠5与∠6、 ∠7与∠8、∠5与∠8、∠6与∠7;共6对. (2)∵∠1与∠2是邻补角 ∴∠1+∠2=180° ∵∠1=150° ∴∠2=30° ∵∠2+∠3=70° ∴∠3=40° ∵∠3与∠4是邻补角 ∴∠4=180°– ∠3=140° 自主完成练习,然后集体交流评价. 及时巩固所学知识,了解学生的学习效果,增强学生应用知识的能力.
环节五 课堂小结 思维导图的形式呈现本节课的主要内容: 在教师的引导下,回顾反思本节课所掌握的知识、技能、思想方法. 培养学生总结知识的能力,巩固新知,形成本节课重点内容框架.
环节六 布置作业 教科书第40页习题2.1 第1、2、3题 学生课后自主完成. 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
