23.4 中位线 教学设计(表格式) 华东师大版数学九年级上册
文档属性
| 名称 | 23.4 中位线 教学设计(表格式) 华东师大版数学九年级上册 | 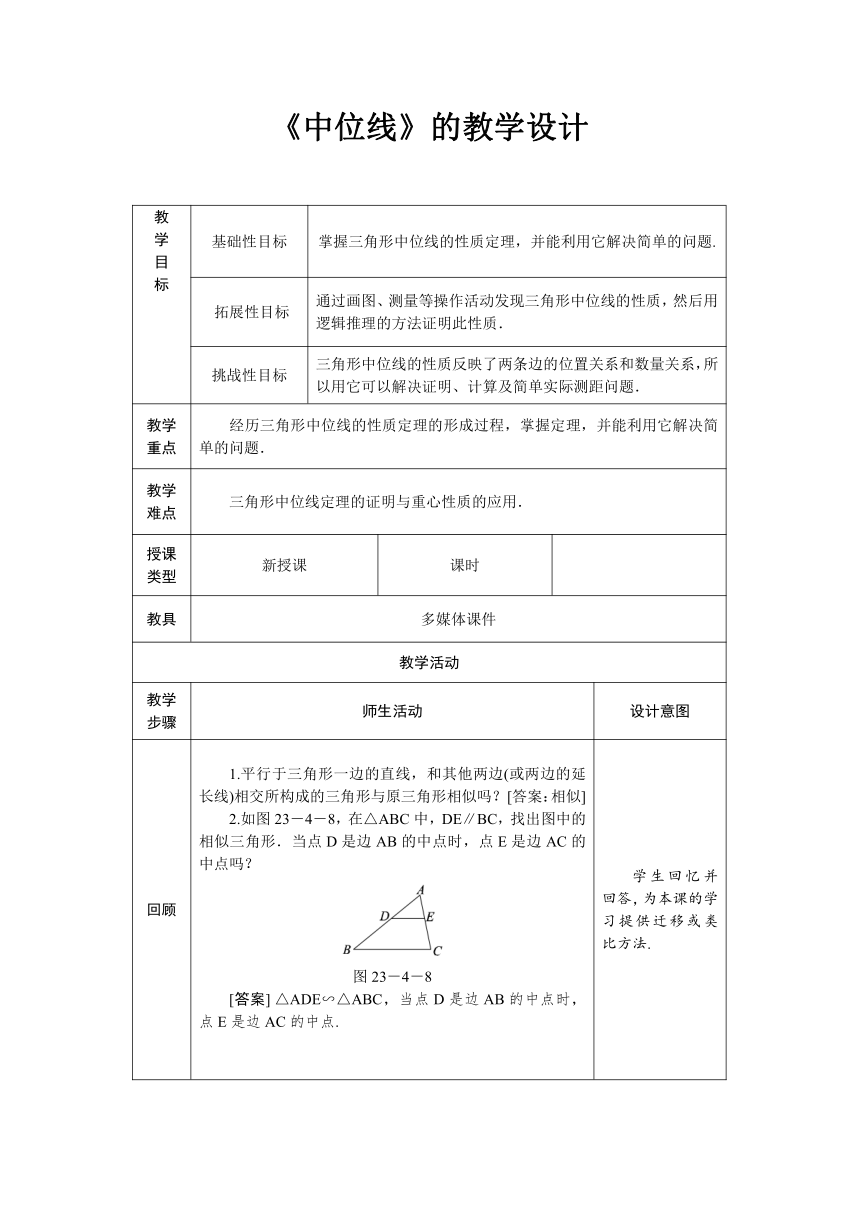 | |
| 格式 | docx | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 10:26:25 | ||
图片预览

文档简介
教 学 目 标 基础性目标 掌握三角形中位线的性质定理,并能利用它解决简单的问题.
拓展性目标 通过画图、测量等操作活动发现三角形中位线的性质,然后用逻辑推理的方法证明此性质.
挑战性目标 三角形中位线的性质反映了两条边的位置关系和数量关系,所以用它可以解决证明、计算及简单实际测距问题.
教学重点 经历三角形中位线的性质定理的形成过程,掌握定理,并能利用它解决简单的问题.
教学难点 三角形中位线定理的证明与重心性质的应用.
授课类型 新授课 课时
教具 多媒体课件
教学活动
教学步骤 师生活动 设计意图
回顾 1.平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似吗?[答案:相似] 2.如图23-4-8,在△ABC中,DE∥BC,找出图中的相似三角形.当点D是边AB的中点时,点E是边AC的中点吗? 图23-4-8 [答案] △ADE∽△ABC,当点D是边AB的中点时,点E是边AC的中点. 学生回忆并回答,为本课的学习提供迁移或类比方法.
《中位线》的教学设计
教学活动
教学步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 问题:你能将任意一个三角形分成四个全等的三角形吗 这四个全等三角形能拼凑成一个平行四边形吗 (板书) (这一问题激发了学生的学习兴趣,学生积极主动地加入课堂教学中,课堂气氛变得较为和谐,课堂也鲜活起来了。) 学生想出了这样的方法:顺次连接三角形每两边的中点,看上去就得到了四个全等的三角形。 利用学生熟悉的情景做问题的背景,学生会对学习更感兴趣,从而激发学生的求知欲,让学生在不知不觉中感受学习数学的乐趣.
活动 二: 实践 探究 交流新知 【探究】如图23-4-10,△ABC中,点D,E分别是边AB,AC的中点,探究DE与BC的位置关系和数量关系. 图23-4-10 师生讨论完成:∵点D,E分别是边AB,AC的中点, ∴==.又∵∠A=∠A,∴△ADE∽△ABC, ∴∠ADE=∠B,=,∴DE∥BC且DE=BC. 引导学生通过自主探究、合作交流达到学习新知的效果.
活动 三: 开放 训练 体现 应用 【应用举例】 1、求证三角形的一条中位线与第三边上的中线互相平分. 已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC. 求证:AE、DF互相平分. 本活动的设计意在学生能根据三角形的中位线的性质定理来完成,进一步熟悉中位线定理的简单应用.
活动 三: 开放 训练 体现 应用 【拓展提升】 例2 如图23-4-12,△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G.求证:==. [答案] 连结ED,∵D,E分别是边BC,AB的中点, ∴DE∥AC,=,∴△DEG∽△ACG, ∴===,∴==. 图23-4-12 图23-4-13 教师做简单的讲解:如图23-4-13,分别取BC,AC的中点D,F,假设BF与AD交于点G′,同理有==,所以有==,即两图中的点G与G′是重合的. 于是,我们有以下结论: 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的. 例3 已知:如图23-4-14,AD,CE分别是△ABC的中线,则S△AEG=__2__S△DEG. 图23-4-14 学以致用,当堂检测,及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.
活动 四: 课堂 总结 反思 【当堂训练】 课本P79中的习题23.4. 当堂检测,及时反馈学习效果.
【知识网络】 提纲挈领,重点突出.
拓展性目标 通过画图、测量等操作活动发现三角形中位线的性质,然后用逻辑推理的方法证明此性质.
挑战性目标 三角形中位线的性质反映了两条边的位置关系和数量关系,所以用它可以解决证明、计算及简单实际测距问题.
教学重点 经历三角形中位线的性质定理的形成过程,掌握定理,并能利用它解决简单的问题.
教学难点 三角形中位线定理的证明与重心性质的应用.
授课类型 新授课 课时
教具 多媒体课件
教学活动
教学步骤 师生活动 设计意图
回顾 1.平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似吗?[答案:相似] 2.如图23-4-8,在△ABC中,DE∥BC,找出图中的相似三角形.当点D是边AB的中点时,点E是边AC的中点吗? 图23-4-8 [答案] △ADE∽△ABC,当点D是边AB的中点时,点E是边AC的中点. 学生回忆并回答,为本课的学习提供迁移或类比方法.
《中位线》的教学设计
教学活动
教学步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 问题:你能将任意一个三角形分成四个全等的三角形吗 这四个全等三角形能拼凑成一个平行四边形吗 (板书) (这一问题激发了学生的学习兴趣,学生积极主动地加入课堂教学中,课堂气氛变得较为和谐,课堂也鲜活起来了。) 学生想出了这样的方法:顺次连接三角形每两边的中点,看上去就得到了四个全等的三角形。 利用学生熟悉的情景做问题的背景,学生会对学习更感兴趣,从而激发学生的求知欲,让学生在不知不觉中感受学习数学的乐趣.
活动 二: 实践 探究 交流新知 【探究】如图23-4-10,△ABC中,点D,E分别是边AB,AC的中点,探究DE与BC的位置关系和数量关系. 图23-4-10 师生讨论完成:∵点D,E分别是边AB,AC的中点, ∴==.又∵∠A=∠A,∴△ADE∽△ABC, ∴∠ADE=∠B,=,∴DE∥BC且DE=BC. 引导学生通过自主探究、合作交流达到学习新知的效果.
活动 三: 开放 训练 体现 应用 【应用举例】 1、求证三角形的一条中位线与第三边上的中线互相平分. 已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC. 求证:AE、DF互相平分. 本活动的设计意在学生能根据三角形的中位线的性质定理来完成,进一步熟悉中位线定理的简单应用.
活动 三: 开放 训练 体现 应用 【拓展提升】 例2 如图23-4-12,△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G.求证:==. [答案] 连结ED,∵D,E分别是边BC,AB的中点, ∴DE∥AC,=,∴△DEG∽△ACG, ∴===,∴==. 图23-4-12 图23-4-13 教师做简单的讲解:如图23-4-13,分别取BC,AC的中点D,F,假设BF与AD交于点G′,同理有==,所以有==,即两图中的点G与G′是重合的. 于是,我们有以下结论: 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的. 例3 已知:如图23-4-14,AD,CE分别是△ABC的中线,则S△AEG=__2__S△DEG. 图23-4-14 学以致用,当堂检测,及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.
活动 四: 课堂 总结 反思 【当堂训练】 课本P79中的习题23.4. 当堂检测,及时反馈学习效果.
【知识网络】 提纲挈领,重点突出.
