北师大版数学六年级下册 第一单元 圆柱与圆锥-第三课时 圆柱的体积课件(共33张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 第一单元 圆柱与圆锥-第三课时 圆柱的体积课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 21:30:35 | ||
图片预览









文档简介
(共33张PPT)
六年级数学下册教学课件(北师版)
第一单元 圆柱与圆锥
第三课时 圆柱的体积
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
(1)圆的面积公式是什么?是怎样得出圆的面积计算公式的?
答:面积公式是:S圆=πr2;把圆等分成若干份,可以拼成 一个近似的长方形。这个长方形的面积就是圆的面积。
答:长方体体积计算公式是:V长=Sh。
(2)已知长方形的底面S和高h,怎样计算长方体的体积?
探索与发现
02
探索与发现
探索与发现
知识点
圆柱体积的意义和计算公式的推导
想一想,怎样计算圆柱的体积呢?
什么是圆柱体呢?
一个圆柱所占空间的大小,叫作这个圆柱的体积。
探索与发现
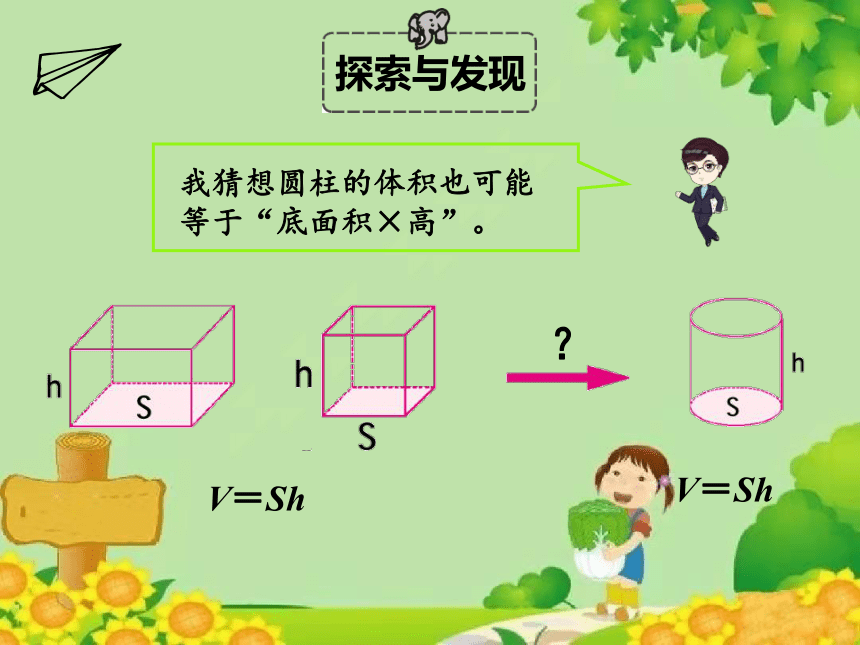
我猜想圆柱的体积也可能等于“底面积×高”。
V=Sh
?
V=Sh
探索与发现
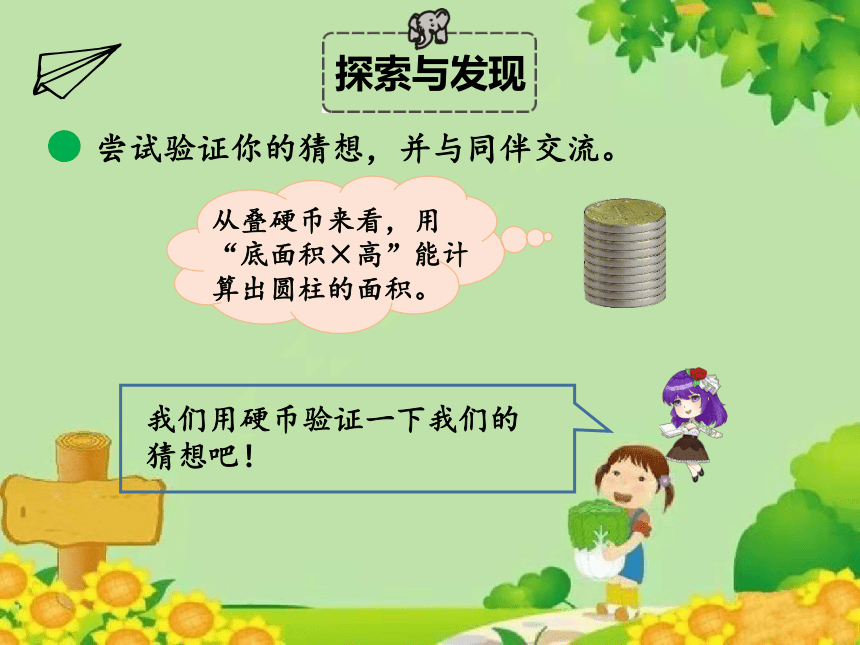
我们用硬币验证一下我们的猜想吧!
从叠硬币来看,用“底面积×高”能计算出圆柱的面积。
尝试验证你的猜想,并与同伴交流。
探索与发现
①把硬币按竖直方向摞起来,底面积是固定的,
每增加一枚硬币,高就增加一些,体积也随
着增加。
从叠硬币来 看,用“底面积×高”能计算出圆柱的体积。
探索与发现
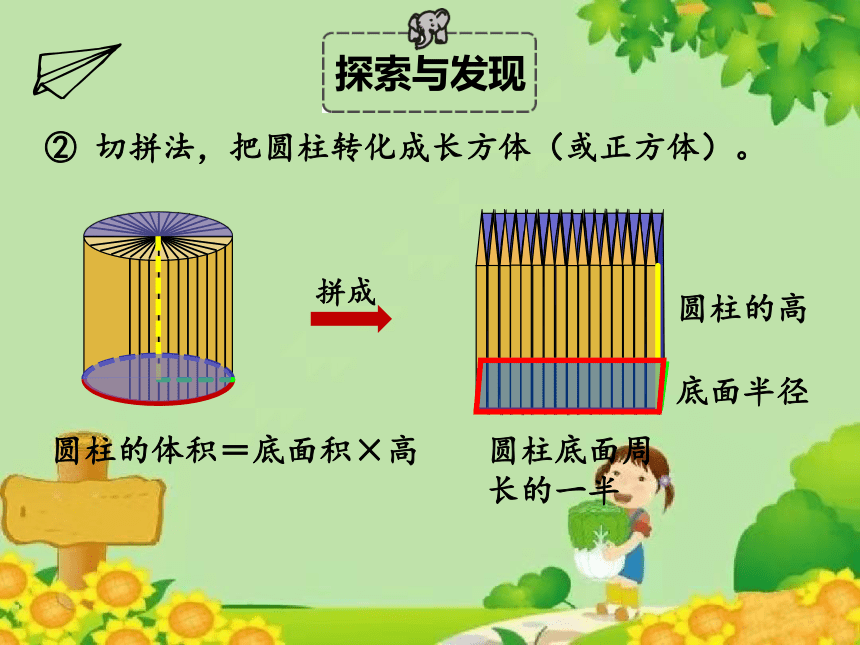
圆柱的体积=底面积×高
圆柱底面周长的一半
圆柱的高
底面半径
② 切拼法,把圆柱转化成长方体(或正方体)。
拼成
探索与发现
我发现了在切拼的过程中,图形的形状变了,但体积的大小没变,即长方体的体积等于圆柱的体积。
我还发现长方体的长是圆柱底面周长的一半(即πr),长方体的宽是圆柱的底面半径(即r),长方体的底面积等于圆柱的底面积(即πr2)。
探索与发现
因此我们可以得到下面的结论:
长方体的高就是圆柱的高。
长方体的体积 = 底面积 × 高
圆柱的体积 = 底面积 × 高
探索与发现
如果用V表示圆柱的体积,S表示圆柱的底面积,h表示圆柱的高,那么圆柱体积的计算公式为:V=Sh。
探索与发现
知识提炼
圆柱的体积=圆柱的底面积×高,用字母表示是V=Sh,也可以这样表示是V=πr2h。
探索与发现
(1)一个圆柱形油桶的底面积是0.8m2,高是1.5m,
体积是( )m3。
小试牛刀
(2)一个圆柱的底面半径是4cm,高是6cm,它的体积是( )cm3。
填空题
1.2
301.44
探索与发现
知识点
圆柱体积公式的应用
尝试验证你的猜想,并与同伴交流。
(1)笑笑了解到一根柱子的底面半径为0.4 m,高为5 m。你能算出它的体积吗?
探索与发现
这道题已知什么?要求什么?能不能根据公式直接计算?
这道题已知底面的半径和高
这道题需要的求的是圆柱的体积。
可以根据V=πr2h直接计算。
探索与发现
可以根据V=πr2h直接计算。我们来算算看吧!
由公式V=Sh和S=πr2可以得出V=πr2h,直接应用此公式可以计算出柱子的体积。
3.14×0.42×5
=2.512(立方米)
答:需要2.512立方米的木材。
探索与发现
(2)从水杯里面量,水杯的底面直径是6 cm,高是16 cm,这个水杯能装多少毫升水?
探索与发现
=3.14×32×16
答:这个水杯能装452.16毫升水。
可以根据V=π( )2h直接计算。我们来算算看吧!
d
2
3.14×( )2×16
2
d
452.16 cm3=452.16 mL
探索与发现
知识提炼
1. 如果已知圆柱的高和半径或直径,可以用公
式 V=πr2h 或 V=π( )2h 来计算出圆柱
的体积。
d
2
2. 容积是容器所能容纳物体的体积,圆柱形
容器容积的求法和圆柱体积的求法是一样的,
只是所需的数据要从容器的里面量。
探索与发现
小试牛刀
博物馆门前一根圆柱形石柱底面半径为4 dm,高为80 dm。这根石柱的体积是多少立方分米?
3.14×42×80=4019.2(dm3)
答:这根石柱的体积是4019.2立方分米。
学以致用
03
学以致用
1.分别计算下列各图形的体积,再说说这几个图形体积计算方法之间的联系。(选自教材P9 T1)
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×(5÷2)2×8
=216(cm3)
都是用V=Sh的公式计算图形的体积的。
学以致用
2.计算下面各圆柱的体积。(选自教材P9 T2)
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×(6÷2)2×10
=282.6(dm3)
学以致用
3.这个杯子能否装下3000 mL的牛奶?(选自教材P9 T3)
侧面积=底面周长×高
3.14×(14÷2)2×20
=3077.2(cm3)
=3077.2(mL)
3077.2 mL>3000 mL
答:这个杯子能装下3000 mL的牛奶。
学以致用
4.光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深是4m。挖出了多少立方米的土?(选自教材P10 T4)
3.14×(3.14÷3.14÷2)2×4=3.14(m3)
答:挖出了3.14立方米的土。
学以致用
5.一个圆柱形的茶杯,茶杯高15厘米,底面半径是3
厘米(从里面量),这个茶杯最多能装多少立方厘米的水?
3.14×32×15=423.9(cm3)
答:这个茶杯最多能装423.9立方厘米的水。
学以致用
1、圆柱的体积=圆柱的底面积×高,用字母表示是V=Sh,也可以这样表示是V=πr2h。
2、如果已知圆柱的高和半径或直径,可以用公
式 V=πr2h 或 V=π( )2h 来计算出圆柱的体积。
d
2
学以致用
3. 容积是容器所能容纳物体的体积,圆柱形容器容积的求法和圆柱体积的求法是一样的,只是所需的数据要从容器的里面量。
课后作业
04
感 谢 观 看
六年级数学下册教学课件(北师版)
第一单元 圆柱与圆锥
第三课时 圆柱的体积
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
(1)圆的面积公式是什么?是怎样得出圆的面积计算公式的?
答:面积公式是:S圆=πr2;把圆等分成若干份,可以拼成 一个近似的长方形。这个长方形的面积就是圆的面积。
答:长方体体积计算公式是:V长=Sh。
(2)已知长方形的底面S和高h,怎样计算长方体的体积?
探索与发现
02
探索与发现
探索与发现
知识点
圆柱体积的意义和计算公式的推导
想一想,怎样计算圆柱的体积呢?
什么是圆柱体呢?
一个圆柱所占空间的大小,叫作这个圆柱的体积。
探索与发现
我猜想圆柱的体积也可能等于“底面积×高”。
V=Sh
?
V=Sh
探索与发现
我们用硬币验证一下我们的猜想吧!
从叠硬币来看,用“底面积×高”能计算出圆柱的面积。
尝试验证你的猜想,并与同伴交流。
探索与发现
①把硬币按竖直方向摞起来,底面积是固定的,
每增加一枚硬币,高就增加一些,体积也随
着增加。
从叠硬币来 看,用“底面积×高”能计算出圆柱的体积。
探索与发现
圆柱的体积=底面积×高
圆柱底面周长的一半
圆柱的高
底面半径
② 切拼法,把圆柱转化成长方体(或正方体)。
拼成
探索与发现
我发现了在切拼的过程中,图形的形状变了,但体积的大小没变,即长方体的体积等于圆柱的体积。
我还发现长方体的长是圆柱底面周长的一半(即πr),长方体的宽是圆柱的底面半径(即r),长方体的底面积等于圆柱的底面积(即πr2)。
探索与发现
因此我们可以得到下面的结论:
长方体的高就是圆柱的高。
长方体的体积 = 底面积 × 高
圆柱的体积 = 底面积 × 高
探索与发现
如果用V表示圆柱的体积,S表示圆柱的底面积,h表示圆柱的高,那么圆柱体积的计算公式为:V=Sh。
探索与发现
知识提炼
圆柱的体积=圆柱的底面积×高,用字母表示是V=Sh,也可以这样表示是V=πr2h。
探索与发现
(1)一个圆柱形油桶的底面积是0.8m2,高是1.5m,
体积是( )m3。
小试牛刀
(2)一个圆柱的底面半径是4cm,高是6cm,它的体积是( )cm3。
填空题
1.2
301.44
探索与发现
知识点
圆柱体积公式的应用
尝试验证你的猜想,并与同伴交流。
(1)笑笑了解到一根柱子的底面半径为0.4 m,高为5 m。你能算出它的体积吗?
探索与发现
这道题已知什么?要求什么?能不能根据公式直接计算?
这道题已知底面的半径和高
这道题需要的求的是圆柱的体积。
可以根据V=πr2h直接计算。
探索与发现
可以根据V=πr2h直接计算。我们来算算看吧!
由公式V=Sh和S=πr2可以得出V=πr2h,直接应用此公式可以计算出柱子的体积。
3.14×0.42×5
=2.512(立方米)
答:需要2.512立方米的木材。
探索与发现
(2)从水杯里面量,水杯的底面直径是6 cm,高是16 cm,这个水杯能装多少毫升水?
探索与发现
=3.14×32×16
答:这个水杯能装452.16毫升水。
可以根据V=π( )2h直接计算。我们来算算看吧!
d
2
3.14×( )2×16
2
d
452.16 cm3=452.16 mL
探索与发现
知识提炼
1. 如果已知圆柱的高和半径或直径,可以用公
式 V=πr2h 或 V=π( )2h 来计算出圆柱
的体积。
d
2
2. 容积是容器所能容纳物体的体积,圆柱形
容器容积的求法和圆柱体积的求法是一样的,
只是所需的数据要从容器的里面量。
探索与发现
小试牛刀
博物馆门前一根圆柱形石柱底面半径为4 dm,高为80 dm。这根石柱的体积是多少立方分米?
3.14×42×80=4019.2(dm3)
答:这根石柱的体积是4019.2立方分米。
学以致用
03
学以致用
1.分别计算下列各图形的体积,再说说这几个图形体积计算方法之间的联系。(选自教材P9 T1)
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×(5÷2)2×8
=216(cm3)
都是用V=Sh的公式计算图形的体积的。
学以致用
2.计算下面各圆柱的体积。(选自教材P9 T2)
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×(6÷2)2×10
=282.6(dm3)
学以致用
3.这个杯子能否装下3000 mL的牛奶?(选自教材P9 T3)
侧面积=底面周长×高
3.14×(14÷2)2×20
=3077.2(cm3)
=3077.2(mL)
3077.2 mL>3000 mL
答:这个杯子能装下3000 mL的牛奶。
学以致用
4.光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深是4m。挖出了多少立方米的土?(选自教材P10 T4)
3.14×(3.14÷3.14÷2)2×4=3.14(m3)
答:挖出了3.14立方米的土。
学以致用
5.一个圆柱形的茶杯,茶杯高15厘米,底面半径是3
厘米(从里面量),这个茶杯最多能装多少立方厘米的水?
3.14×32×15=423.9(cm3)
答:这个茶杯最多能装423.9立方厘米的水。
学以致用
1、圆柱的体积=圆柱的底面积×高,用字母表示是V=Sh,也可以这样表示是V=πr2h。
2、如果已知圆柱的高和半径或直径,可以用公
式 V=πr2h 或 V=π( )2h 来计算出圆柱的体积。
d
2
学以致用
3. 容积是容器所能容纳物体的体积,圆柱形容器容积的求法和圆柱体积的求法是一样的,只是所需的数据要从容器的里面量。
课后作业
04
感 谢 观 看
