苏教版数学五年级下册 第一单元 简易方程-第三课时 列方程解决简单实际问题(一)课件 (共24张PPT)
文档属性
| 名称 | 苏教版数学五年级下册 第一单元 简易方程-第三课时 列方程解决简单实际问题(一)课件 (共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 21:32:18 | ||
图片预览








文档简介
(共24张PPT)
五年级数学下册教学课件(苏教版)
第一单元 简易方程
第三课时 列方程解决简单实际问题(一)
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
解方程。
x+56=102 x-970=270 15x=3 x÷0.8=1.25
x+56=102
解:x+56-56=102-56
x=46
x-970=270
解:x-970+970=270+970
x= 1240
情景导学
解方程。
x+56=102 x-970=270 15x=3 x÷0.8=1.25
x+56=102
解:x+56-56=102-56
x=46
x-970=270
解:x-970+970=270+970
x= 1240
探索与发现
02
探索与发现
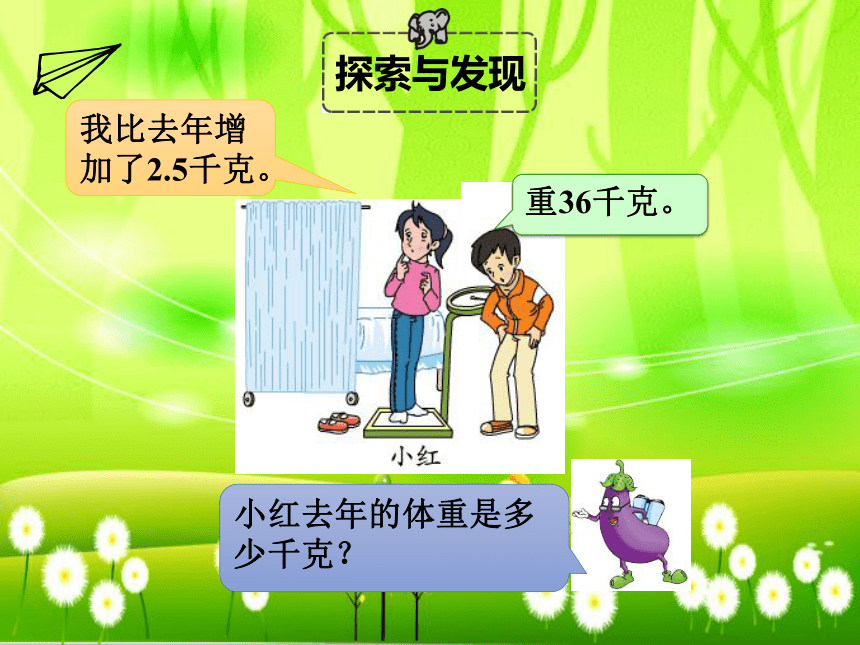
重36千克。
我比去年增加了2.5千克。
小红去年的体重是多少千克?
探索与发现
先说说题中的条件和问题, 再找出数量之间的相等关系。
去年的体重加上2.5 千克等于今年的体重。
今年的体重减去年的体重等于 2.5 千克。
探索与发现
去年的体重加上2.5 千克等于今年的体重。
可以根据“去年的体重 + 2.5 = 今年的体重” 列出方程。
去年的体重不知道, 可以设去年体重为 x 千克。
解: 设小红去年的体重是 x 千克。
x + 2.5 = 36
x = 36-2.5
x = 33.5
答:小红去年的体重是 33.5 千克。
探索与发现
今年的体重减去年的体重等于 2.5 千克。
根据“今年的体重 - 去年的体重 = 2.5” 可以怎样列方程? 又该怎样解?
解: 设小红去年的体重是 x 千克。
36-x = 2.5
探索与发现
36-x = 2.5
36-x+x = 2.5+x
x = 33.5
答:小红去年的体重是 33.5 千克。
36= 2.5+x
2.5+x =36
探索与发现
先检查方程列得是否正确,再检验方程的解。
你打算怎样检验? 与同学交流。
看两种方程的解答结果是否相同。
探索与发现
列方程解决实际问题时要注意什么?
先弄清题意,找出未知量,并用字母表示。
要根据题中数量之间的相等关系列方程。
求出答案后,还要检验结果是否正确。
学以致用
03
学以致用
1.一头蓝鲸重 165 吨,大约是一头非洲象的 33 倍。 这头非洲象大约重多少吨?(先把数量间的相等关系填写完整,再列方程解答)
( )的体重 × 33 = ( )的体重
非洲象
蓝鲸
解:设这头非洲象大约重x吨。
33x = 165
33x ÷33= 165÷33
x= 5
答:这头非洲象大约重5吨。
学以致用
2.王林的身高是1.8米,比小刚高0.05米。小刚的身高是多少米?
解:设小刚的身高是x米。
x+0.05 = 1.8
x= 1.8-0.05
x= 1.75
答:小刚的身高是1.75米。
学以致用
3.某市居民用电每千瓦·时的价格是0.52元,芳芳家上月付电费23.4元,用电多少千瓦·时?
解:设用电x千瓦·时。
0.52x=23.4
0.52x÷0.52=23.4÷0.52
x=45
答:用电45千瓦·时。
单价×用电量=总价
学以致用
宽×1.5=长
解:设宽应是x厘米。
1.5x=144
1.5x÷1.5=144÷1.5
x=96
答:宽应是96厘米。
4.中华人民共和国国旗的长应是宽的1.5倍。一面国旗长144厘米,宽应是多少厘米?
学以致用
5.一种饮料有两种包装规格,大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元,比大瓶便宜3.2元。
(1)小瓶的容量是多少升?
解:设小瓶的容量是x升。
x×3=1.5
x×3÷3=1.5÷3
x=0.5
答:小瓶的容量是0.5升。
学以致用
5.一种饮料有两种包装规格,大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元,比大瓶便宜3.2元。
(2)大瓶的单价是多少元?
解:设大瓶的单价是x元。
x-3.2=1.8
x-3.2+3.2=1.8+3.2
x=5
答:大瓶的单价是5元。
学以致用
1.列方程解决实际问题的一般步骤:
(1)设未知数;
(2)找出题目中的等量关系;
(3)列方程;
(4)解方程;
(5)检验;
(6)作答。
学以致用
2.列一步计算的方程解决实际问题:
(1)相差关系的实际问题,有两种列方程的方法,即x±a=b和b±x=a的形式;
(2)倍数关系的实际问题,通常依据“一倍数×倍数=几倍数”或“几倍数÷倍数=一倍数”列方程。
课后作业
04
感 谢 观 看
五年级数学下册教学课件(苏教版)
第一单元 简易方程
第三课时 列方程解决简单实际问题(一)
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
解方程。
x+56=102 x-970=270 15x=3 x÷0.8=1.25
x+56=102
解:x+56-56=102-56
x=46
x-970=270
解:x-970+970=270+970
x= 1240
情景导学
解方程。
x+56=102 x-970=270 15x=3 x÷0.8=1.25
x+56=102
解:x+56-56=102-56
x=46
x-970=270
解:x-970+970=270+970
x= 1240
探索与发现
02
探索与发现
重36千克。
我比去年增加了2.5千克。
小红去年的体重是多少千克?
探索与发现
先说说题中的条件和问题, 再找出数量之间的相等关系。
去年的体重加上2.5 千克等于今年的体重。
今年的体重减去年的体重等于 2.5 千克。
探索与发现
去年的体重加上2.5 千克等于今年的体重。
可以根据“去年的体重 + 2.5 = 今年的体重” 列出方程。
去年的体重不知道, 可以设去年体重为 x 千克。
解: 设小红去年的体重是 x 千克。
x + 2.5 = 36
x = 36-2.5
x = 33.5
答:小红去年的体重是 33.5 千克。
探索与发现
今年的体重减去年的体重等于 2.5 千克。
根据“今年的体重 - 去年的体重 = 2.5” 可以怎样列方程? 又该怎样解?
解: 设小红去年的体重是 x 千克。
36-x = 2.5
探索与发现
36-x = 2.5
36-x+x = 2.5+x
x = 33.5
答:小红去年的体重是 33.5 千克。
36= 2.5+x
2.5+x =36
探索与发现
先检查方程列得是否正确,再检验方程的解。
你打算怎样检验? 与同学交流。
看两种方程的解答结果是否相同。
探索与发现
列方程解决实际问题时要注意什么?
先弄清题意,找出未知量,并用字母表示。
要根据题中数量之间的相等关系列方程。
求出答案后,还要检验结果是否正确。
学以致用
03
学以致用
1.一头蓝鲸重 165 吨,大约是一头非洲象的 33 倍。 这头非洲象大约重多少吨?(先把数量间的相等关系填写完整,再列方程解答)
( )的体重 × 33 = ( )的体重
非洲象
蓝鲸
解:设这头非洲象大约重x吨。
33x = 165
33x ÷33= 165÷33
x= 5
答:这头非洲象大约重5吨。
学以致用
2.王林的身高是1.8米,比小刚高0.05米。小刚的身高是多少米?
解:设小刚的身高是x米。
x+0.05 = 1.8
x= 1.8-0.05
x= 1.75
答:小刚的身高是1.75米。
学以致用
3.某市居民用电每千瓦·时的价格是0.52元,芳芳家上月付电费23.4元,用电多少千瓦·时?
解:设用电x千瓦·时。
0.52x=23.4
0.52x÷0.52=23.4÷0.52
x=45
答:用电45千瓦·时。
单价×用电量=总价
学以致用
宽×1.5=长
解:设宽应是x厘米。
1.5x=144
1.5x÷1.5=144÷1.5
x=96
答:宽应是96厘米。
4.中华人民共和国国旗的长应是宽的1.5倍。一面国旗长144厘米,宽应是多少厘米?
学以致用
5.一种饮料有两种包装规格,大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元,比大瓶便宜3.2元。
(1)小瓶的容量是多少升?
解:设小瓶的容量是x升。
x×3=1.5
x×3÷3=1.5÷3
x=0.5
答:小瓶的容量是0.5升。
学以致用
5.一种饮料有两种包装规格,大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元,比大瓶便宜3.2元。
(2)大瓶的单价是多少元?
解:设大瓶的单价是x元。
x-3.2=1.8
x-3.2+3.2=1.8+3.2
x=5
答:大瓶的单价是5元。
学以致用
1.列方程解决实际问题的一般步骤:
(1)设未知数;
(2)找出题目中的等量关系;
(3)列方程;
(4)解方程;
(5)检验;
(6)作答。
学以致用
2.列一步计算的方程解决实际问题:
(1)相差关系的实际问题,有两种列方程的方法,即x±a=b和b±x=a的形式;
(2)倍数关系的实际问题,通常依据“一倍数×倍数=几倍数”或“几倍数÷倍数=一倍数”列方程。
课后作业
04
感 谢 观 看
