2023年广东省东莞中考数学仿真模拟冲刺试卷(含答案)
文档属性
| 名称 | 2023年广东省东莞中考数学仿真模拟冲刺试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 121.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 00:00:00 | ||
图片预览



文档简介
2023年广东省东莞中考数学 仿真 模拟冲刺试卷
一、选择题(本大题共10小题,共30.0分)
1. 在,,,这四个数中,最小的数是( )
A. B. C. D.
2. 古典园林中的花窗通常利用对称构图,体现对称美下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B.
C. D.
4. 下列命题是真命题的是( )
A. 在同一平面内,过直线上一点可以画出无数条直线与已知直线垂直
B. 若是负数,则
C. 同位角相等
D. 若,则或
5. 要使式子有意义,的取值范围是( )
A. B. C. D.
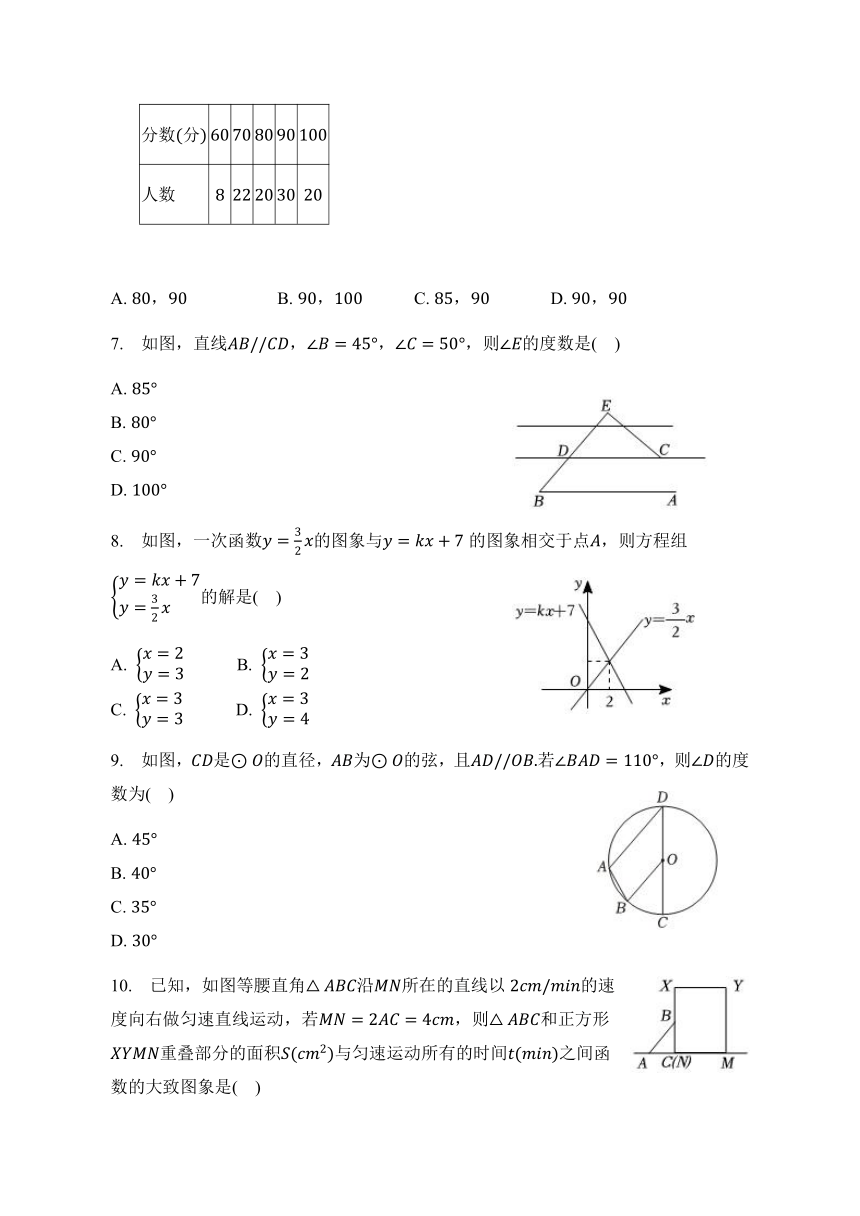
6. 今年是我国现行宪法公布施行周年为贯彻党的二十大精神,强化宪法意识,弘扬宪法精神,推动宪法实施,某学校开展法律知识竞赛活动,全校一共名学生参与其中,得分情况如下表,则分数的中位数和众数分别是( )
分数分
人数
A. , B. , C. , D. ,
7. 如图,直线,,,则的度数是( )
A.
B.
C.
D.
8. 如图,一次函数的图象与的图象相交于点,则方程组的解是( )
A. B.
C. D.
9. 如图,是的直径,为的弦,且若,则的度数为( )
A.
B.
C.
D.
10. 已知,如图等腰直角沿所在的直线以的速度向右做匀速直线运动,若,则和正方形重叠部分的面积与匀速运动所有的时间之间函数的大致图象是( )
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
11. 因式分解: ______ .
12. 在平面直角坐标系中,若点与点关于轴对称,则点的坐标是______ .
13. 在中,,,, ______ .
14. 如图所示的扇形中,,过点作,交于点,若,则阴影部分的面积为 .
15. 如图,在菱形中,,对角线、相交于点,点在线段上,且,点为线段上的一个动点,则的最小值是 .
三、解答题(本大题共8小题,共75.0分)
16. 计算:.
17. 解不等式组:,并写出该不等式组的整数解.
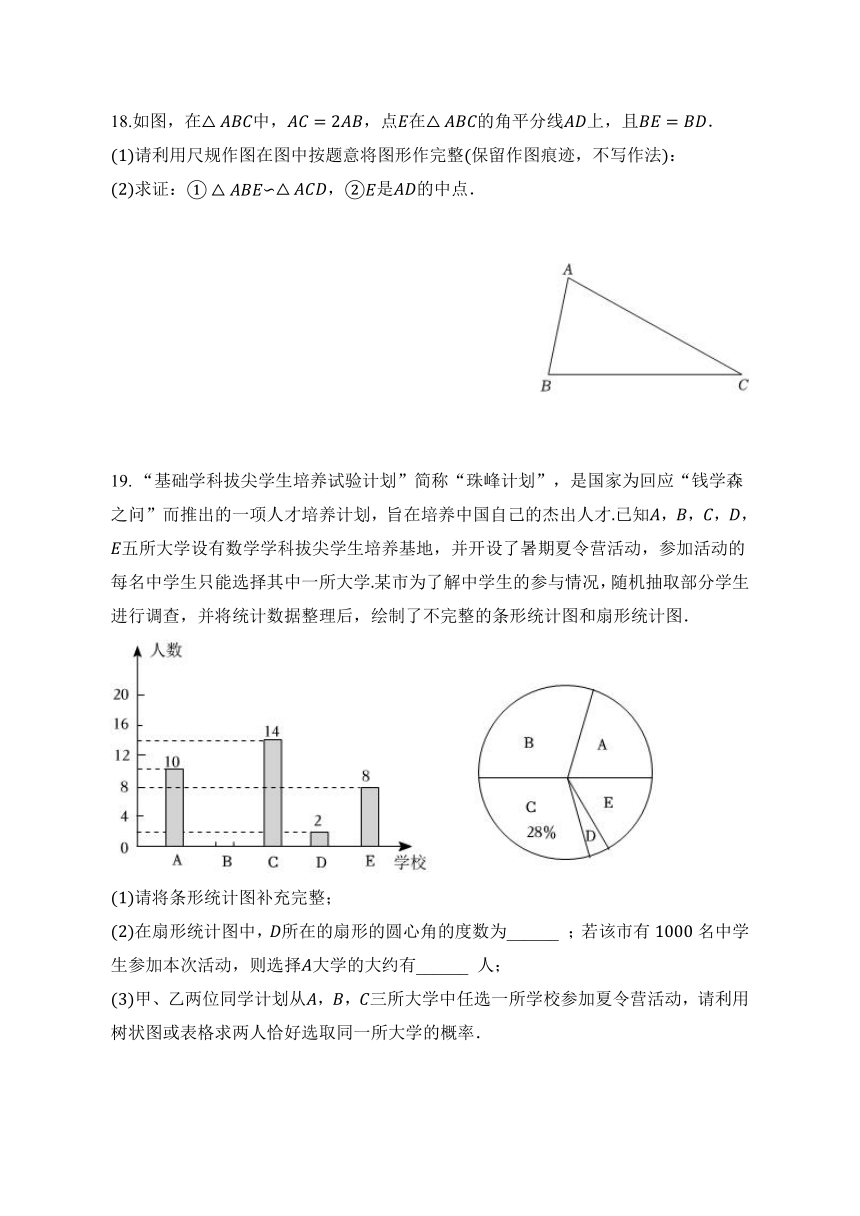
18.如图,在中,,点在的角平分线上,且.
请利用尺规作图在图中按题意将图形作完整保留作图痕迹,不写作法:
求证:∽,是的中点.
19. “基础学科拔尖学生培养试验计划”简称“珠峰计划”,是国家为回应“钱学森之问”而推出的一项人才培养计划,旨在培养中国自己的杰出人才已知,,,,五所大学设有数学学科拔尖学生培养基地,并开设了暑期夏令营活动,参加活动的每名中学生只能选择其中一所大学某市为了解中学生的参与情况,随机抽取部分学生进行调查,并将统计数据整理后,绘制了不完整的条形统计图和扇形统计图.
请将条形统计图补充完整;
在扇形统计图中,所在的扇形的圆心角的度数为______ ;若该市有名中学生参加本次活动,则选择大学的大约有______ 人;
甲、乙两位同学计划从,,三所大学中任选一所学校参加夏令营活动,请利用树状图或表格求两人恰好选取同一所大学的概率.
20.某景区农家乐有客房间供游客居住,当每间客房的定价为每天元时,客房会全部住满当每间客房每天定价每增加元时,就会有间客房空置注:农家乐客房是以整间出租的
若某天每间客房的定价增加了元,则这天客房收入为______ 元;
设某天每间客房的定价增加了元,这天客房收入元,求与的函数解析式,当每个房间的定价为每天多少元时,有最大值?最大值是多少?
如果政府规定该农家乐入住率超过可以获得每间元的政府补贴,某天客房收入元,试求这天农家乐可获得政府补贴多少元?
21. 如图,已知是的直径,过上的点的切线交的延长线于,于且交于.
若,,求线段和的长度;
求证:.
22. 如图,已知直线经过点,与双曲线交于点过点作轴的平行线分别交双曲线和于点、.
求的值和直线的解析式;
若点在直线上,求证:∽;
是否存在实数,使得?若存在,请求出所有满足条件的的值;若不存在,请说明理由.
23.如图,在平面直角坐标系中,抛物线的顶点为,与轴交于点,线段轴,交该抛物线于点.
求该抛物线的解析式;
当二次函数的自变量满足时,此函数的最大值为,最小值为,且,求的值;
平移抛物线,使其顶点始终在直线上移动,当平移后的抛物线与射线只有一个公共点时,设此时抛物线的顶点的横坐标为,请直接写出的取值范围.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.解:
.
17.解:,
解得:,
,
,
,
解得:,
,
,
,
,
不等式组的解集为:,
该不等式组的整数解为,,,.
18.作法:以点为圆心,适当长为半径作弧交于点,交于点,
分别以点、点为圆心,大于的长为半径弧,两弧在内部交于点,
作射线交于点,
以点为圆心,的长为半径作弧交于点,
连接,
线段和线段就是所求的图形.
证明:连接、,
在和中,
,
≌,
,
是的角平分线,
由作图得,
线段、线段就是所求的图形.
证明:,
,
平分,点在上,
,
,
,
∽.
∽,,
,
,
,
是的中点.
19.解:本次抽取的学生有:人,
其中选择的学生有:人,
补全的条形统计图如右图所示;
在扇形统计图中,所在的扇形的圆心角的度数为:,
该市有名中学生参加本次活动,则选择大学的大约有:人,
故答案为:,;
树状图如下所示:
由上可得,一共有种等可能性,其中两人恰好选取同一所大学的可能性有种,
两人恰好选取同一所大学的概率为.
20.解:若某天每间客房的定价增加了元,
则这天宾馆客房住满了间,
客房收入元.
故答案为:.
设某天每间客房的定价增加了元时,
则客房共住满了间,
这天宾馆客房收入
,
故当时,取得最大值;此时每个房间的定价为元,
的最大值是元.
当时,,
解得或,
当时,则有间客房住满了客人,
此时的入住率为,
故得不到政府补贴;
当时,则有间客房住满了客人,
此时的入住率为,
故这天农家乐可获得政府补贴元.
21.解:是的切线,
,
,
,是的切线,
∽,
,
,
在中,,
,
直径所对的圆周角度,,
,
∽,
,
将,,,代入得
;
证明:连接,,两直线的交点为
,,
∽,
,,
直径所对的圆周角度,
四边形是个长方形,
,
,
是半径,是直径,
.
22.解:在双曲线上,
,
设直线的解析式为,
则,
解得,
直线的解析式为;
证明:点,点在直线上,
,
解得,
,
,,,,
,:::,
∽;
解:存在实数,使得.
,
点、的纵坐标都为,
将代入和,
得和,
、的坐标分别为,,
当时,
,,
,,
,
,
整理,得,
解得:,
,
,
当时,
,,
,,
,
,
整理,得,解得,
大于,
,
存在实数或使得.
23.解:,
抛物线的顶点为,
抛物线的顶点为,
,,
,,
该抛物线的解析式为;
抛物线的对称轴为,
当时,,,
,
,
解得:舍去;
当,即时,,,
,
,
解得舍;
当,即时,,,
,
解得:或舍;
;
当,即时,,,
,
解得舍或;
;
综上所述,的值为或;
如图:
在中,令得,
,
抛物线对称轴为直线,轴,
,
,
直线解析式为,直线解析式为,
平移后的新抛物线顶点的横坐标为,顶点始终在直线上移动,
新抛物线顶点为,
新抛物线解析式为,
当只有一个解时,平移后的抛物线与射线只有一个公共点,
此时有两个相等的实数解,即有两个相等实数解,
,
解得;
当平移后的抛物线过时,把代入得:
,
解得或,
由图可知,当时,平移后的抛物线与射线只有一个公共点;
综上所述,的取值范围是或.
一、选择题(本大题共10小题,共30.0分)
1. 在,,,这四个数中,最小的数是( )
A. B. C. D.
2. 古典园林中的花窗通常利用对称构图,体现对称美下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B.
C. D.
4. 下列命题是真命题的是( )
A. 在同一平面内,过直线上一点可以画出无数条直线与已知直线垂直
B. 若是负数,则
C. 同位角相等
D. 若,则或
5. 要使式子有意义,的取值范围是( )
A. B. C. D.
6. 今年是我国现行宪法公布施行周年为贯彻党的二十大精神,强化宪法意识,弘扬宪法精神,推动宪法实施,某学校开展法律知识竞赛活动,全校一共名学生参与其中,得分情况如下表,则分数的中位数和众数分别是( )
分数分
人数
A. , B. , C. , D. ,
7. 如图,直线,,,则的度数是( )
A.
B.
C.
D.
8. 如图,一次函数的图象与的图象相交于点,则方程组的解是( )
A. B.
C. D.
9. 如图,是的直径,为的弦,且若,则的度数为( )
A.
B.
C.
D.
10. 已知,如图等腰直角沿所在的直线以的速度向右做匀速直线运动,若,则和正方形重叠部分的面积与匀速运动所有的时间之间函数的大致图象是( )
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
11. 因式分解: ______ .
12. 在平面直角坐标系中,若点与点关于轴对称,则点的坐标是______ .
13. 在中,,,, ______ .
14. 如图所示的扇形中,,过点作,交于点,若,则阴影部分的面积为 .
15. 如图,在菱形中,,对角线、相交于点,点在线段上,且,点为线段上的一个动点,则的最小值是 .
三、解答题(本大题共8小题,共75.0分)
16. 计算:.
17. 解不等式组:,并写出该不等式组的整数解.
18.如图,在中,,点在的角平分线上,且.
请利用尺规作图在图中按题意将图形作完整保留作图痕迹,不写作法:
求证:∽,是的中点.
19. “基础学科拔尖学生培养试验计划”简称“珠峰计划”,是国家为回应“钱学森之问”而推出的一项人才培养计划,旨在培养中国自己的杰出人才已知,,,,五所大学设有数学学科拔尖学生培养基地,并开设了暑期夏令营活动,参加活动的每名中学生只能选择其中一所大学某市为了解中学生的参与情况,随机抽取部分学生进行调查,并将统计数据整理后,绘制了不完整的条形统计图和扇形统计图.
请将条形统计图补充完整;
在扇形统计图中,所在的扇形的圆心角的度数为______ ;若该市有名中学生参加本次活动,则选择大学的大约有______ 人;
甲、乙两位同学计划从,,三所大学中任选一所学校参加夏令营活动,请利用树状图或表格求两人恰好选取同一所大学的概率.
20.某景区农家乐有客房间供游客居住,当每间客房的定价为每天元时,客房会全部住满当每间客房每天定价每增加元时,就会有间客房空置注:农家乐客房是以整间出租的
若某天每间客房的定价增加了元,则这天客房收入为______ 元;
设某天每间客房的定价增加了元,这天客房收入元,求与的函数解析式,当每个房间的定价为每天多少元时,有最大值?最大值是多少?
如果政府规定该农家乐入住率超过可以获得每间元的政府补贴,某天客房收入元,试求这天农家乐可获得政府补贴多少元?
21. 如图,已知是的直径,过上的点的切线交的延长线于,于且交于.
若,,求线段和的长度;
求证:.
22. 如图,已知直线经过点,与双曲线交于点过点作轴的平行线分别交双曲线和于点、.
求的值和直线的解析式;
若点在直线上,求证:∽;
是否存在实数,使得?若存在,请求出所有满足条件的的值;若不存在,请说明理由.
23.如图,在平面直角坐标系中,抛物线的顶点为,与轴交于点,线段轴,交该抛物线于点.
求该抛物线的解析式;
当二次函数的自变量满足时,此函数的最大值为,最小值为,且,求的值;
平移抛物线,使其顶点始终在直线上移动,当平移后的抛物线与射线只有一个公共点时,设此时抛物线的顶点的横坐标为,请直接写出的取值范围.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.解:
.
17.解:,
解得:,
,
,
,
解得:,
,
,
,
,
不等式组的解集为:,
该不等式组的整数解为,,,.
18.作法:以点为圆心,适当长为半径作弧交于点,交于点,
分别以点、点为圆心,大于的长为半径弧,两弧在内部交于点,
作射线交于点,
以点为圆心,的长为半径作弧交于点,
连接,
线段和线段就是所求的图形.
证明:连接、,
在和中,
,
≌,
,
是的角平分线,
由作图得,
线段、线段就是所求的图形.
证明:,
,
平分,点在上,
,
,
,
∽.
∽,,
,
,
,
是的中点.
19.解:本次抽取的学生有:人,
其中选择的学生有:人,
补全的条形统计图如右图所示;
在扇形统计图中,所在的扇形的圆心角的度数为:,
该市有名中学生参加本次活动,则选择大学的大约有:人,
故答案为:,;
树状图如下所示:
由上可得,一共有种等可能性,其中两人恰好选取同一所大学的可能性有种,
两人恰好选取同一所大学的概率为.
20.解:若某天每间客房的定价增加了元,
则这天宾馆客房住满了间,
客房收入元.
故答案为:.
设某天每间客房的定价增加了元时,
则客房共住满了间,
这天宾馆客房收入
,
故当时,取得最大值;此时每个房间的定价为元,
的最大值是元.
当时,,
解得或,
当时,则有间客房住满了客人,
此时的入住率为,
故得不到政府补贴;
当时,则有间客房住满了客人,
此时的入住率为,
故这天农家乐可获得政府补贴元.
21.解:是的切线,
,
,
,是的切线,
∽,
,
,
在中,,
,
直径所对的圆周角度,,
,
∽,
,
将,,,代入得
;
证明:连接,,两直线的交点为
,,
∽,
,,
直径所对的圆周角度,
四边形是个长方形,
,
,
是半径,是直径,
.
22.解:在双曲线上,
,
设直线的解析式为,
则,
解得,
直线的解析式为;
证明:点,点在直线上,
,
解得,
,
,,,,
,:::,
∽;
解:存在实数,使得.
,
点、的纵坐标都为,
将代入和,
得和,
、的坐标分别为,,
当时,
,,
,,
,
,
整理,得,
解得:,
,
,
当时,
,,
,,
,
,
整理,得,解得,
大于,
,
存在实数或使得.
23.解:,
抛物线的顶点为,
抛物线的顶点为,
,,
,,
该抛物线的解析式为;
抛物线的对称轴为,
当时,,,
,
,
解得:舍去;
当,即时,,,
,
,
解得舍;
当,即时,,,
,
解得:或舍;
;
当,即时,,,
,
解得舍或;
;
综上所述,的值为或;
如图:
在中,令得,
,
抛物线对称轴为直线,轴,
,
,
直线解析式为,直线解析式为,
平移后的新抛物线顶点的横坐标为,顶点始终在直线上移动,
新抛物线顶点为,
新抛物线解析式为,
当只有一个解时,平移后的抛物线与射线只有一个公共点,
此时有两个相等的实数解,即有两个相等实数解,
,
解得;
当平移后的抛物线过时,把代入得:
,
解得或,
由图可知,当时,平移后的抛物线与射线只有一个公共点;
综上所述,的取值范围是或.
同课章节目录
