垂径定理[上学期]
图片预览





文档简介
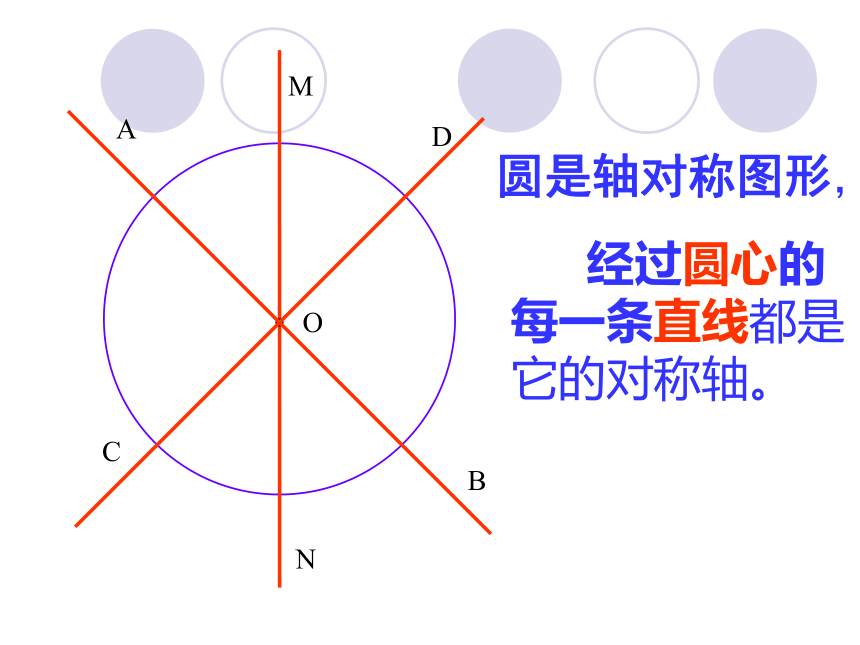
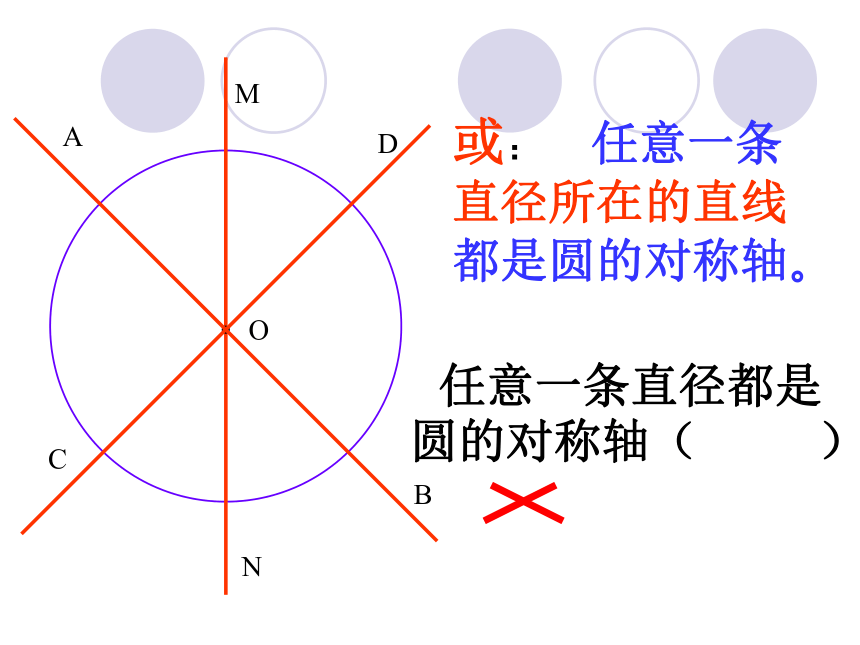
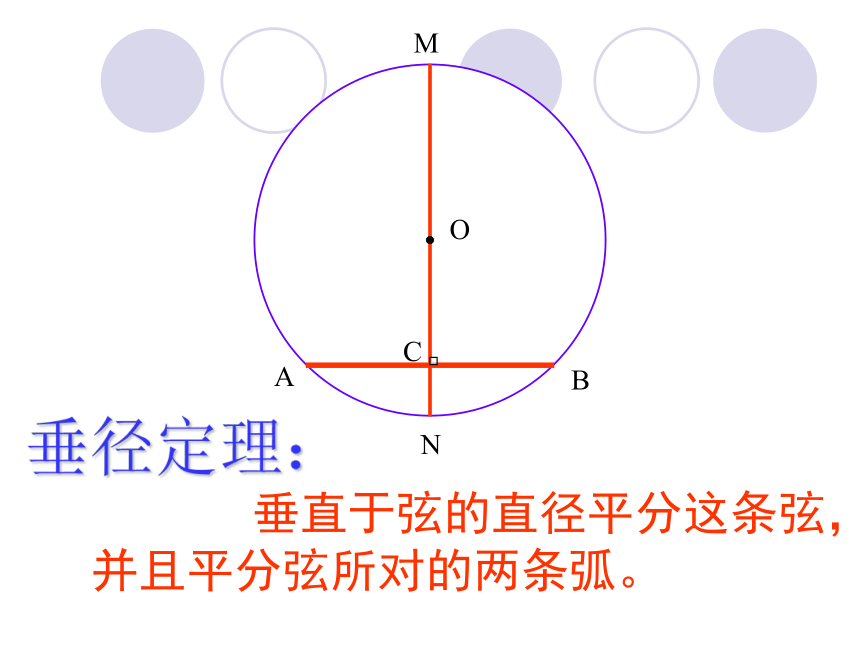
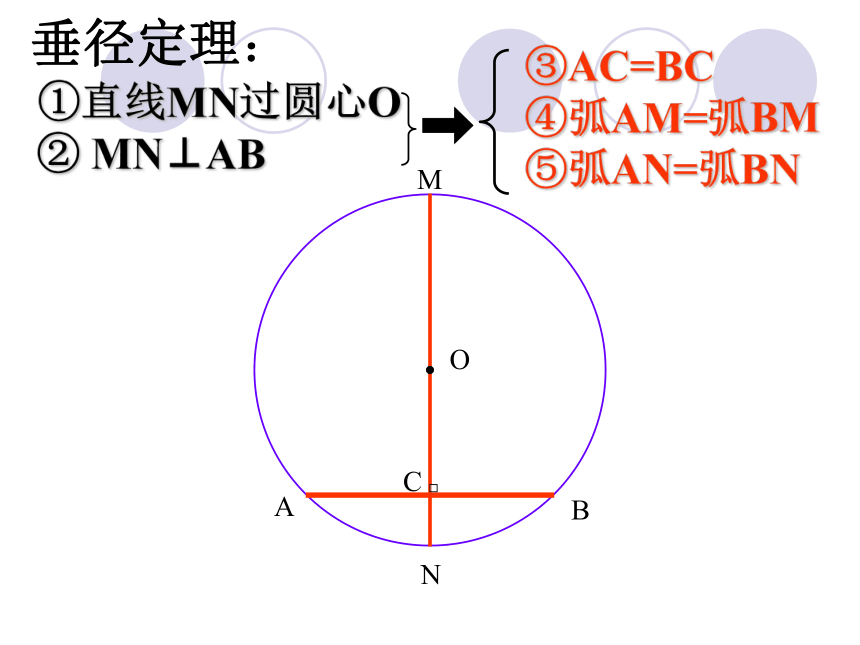
课件32张PPT。O圆除了是旋转对称图形外,还是轴对称图形提问:圆是什么对称图形?OACBNMD圆是轴对称图形, 经过圆心的每一条直线都是它的对称轴。OACBNMD或: 任意一条直径所在的直线都是圆的对称轴。 任意一条直径都是圆的对称轴( )MOACBN 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:MOACBN①直线MN过圆心O ② MN⊥AB③AC=BC
④弧AM=弧BM
⑤弧AN=弧BN垂径定理: 如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线MN过圆心O ② MN⊥AB③AC=BC
④弧AM=弧BM
⑤弧AN=弧BN垂径定理: 课题:垂直于弦的直径(2)垂径定理的推论
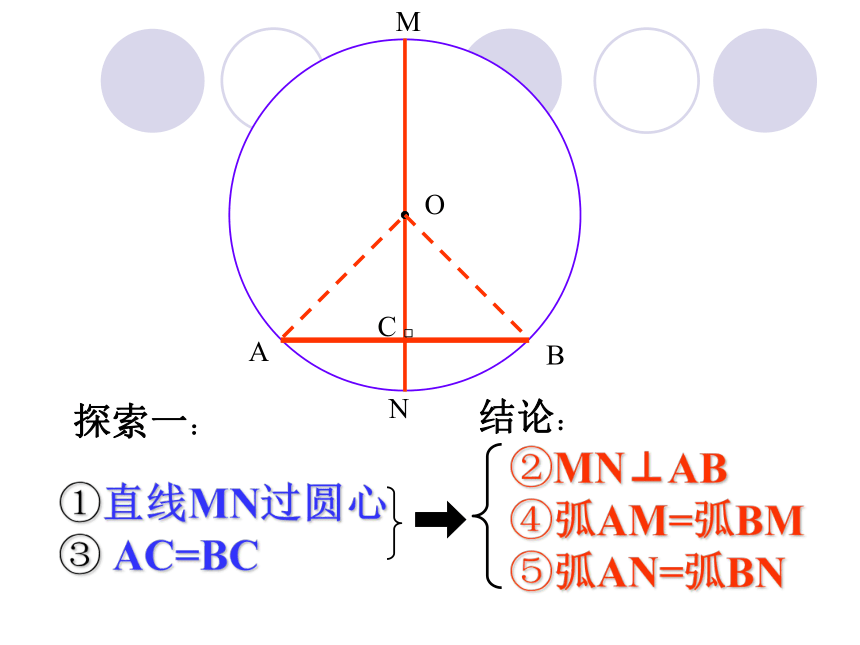
MOACBN①直线MN过圆心③ AC=BC
②MN⊥AB
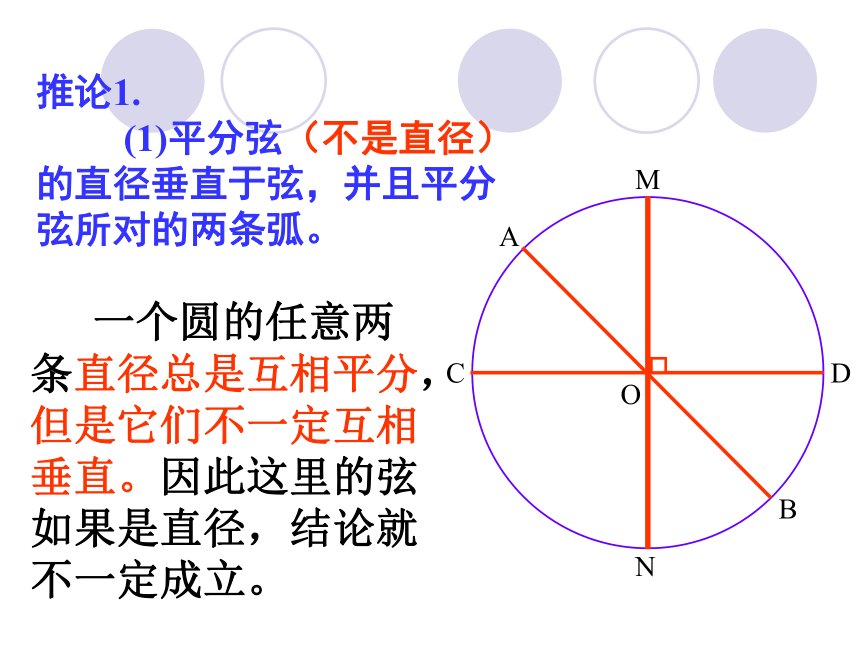
④弧AM=弧BM ⑤弧AN=弧BN探索一:结论:推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。OABMN一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。CDMOACBN② MN⊥AB ③ AC=BC
①直线MN过圆心O
④弧AM=弧BM
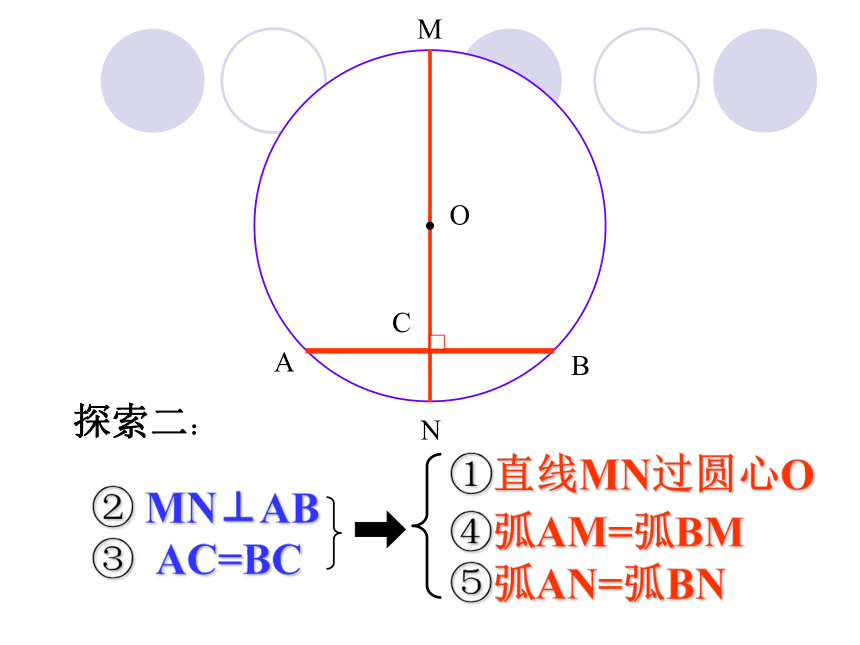
⑤弧AN=弧BN探索二:推论1: (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;MOACBN② MN⊥AB ③ AC=BC ④弧AM=弧BM①直线MN过圆心O
⑤弧AN=弧BN探索三:推论1: (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
推论1:
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;.
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
推论2. 圆的两条平行弦所夹的弧相等。
推论2. 圆的两条平行弦所夹的弧相等。
MOABNCD作直径MN垂直于弦AB∵AB∥CD ∴直径MN也垂直于弦CD于是 弧AM=弧BM, 弧CM=弧DM∴弧AM-弧CM =弧BM-弧DM 即 弧AC=弧BDCDABE例:平分已知弧AB已知:弧AB
作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点CDABEFG变式一: 求弧AB的四等分点。 mnCDABMTEFGHNP错在哪里?等分弧时一定要作弧所夹弦的垂直平分线。●作AB的垂直平分线CD。●作AT.BT的垂直
平分线EF.GHCABE变式二:你能确定 弧AB的圆心吗?mnDCABEmnO你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据: 已知:AB、CD是⊙O的两条平行弦,
MN是AB的垂直平分线。
求证:MN垂直平分CD。 MOANCDB 圆内平行弦的垂直平分线是互相重合的。 已知:AB、CD是⊙O的两条平行弦,
MN是AB的垂直平分线。
求证:MN垂直平分CD。 MOABNCD分析:MN是AB的垂直平分线 则有: MN过圆心O是直径由AB∥CD, MN⊥AB 则有:MN⊥CD由垂径定理,得MN平分CD所以:MN垂直平分CDMOBNCD证明: ∵ MN是AB的垂直平分线 ∴ MN过圆心是直径∴MN⊥CD∴ MN平分CDA∵AB∥CD,MN⊥AB
∴MN垂直平分CD
课堂小结:
本节课探索发现了垂径定理的推论1和推
论2,并且运用推论1等分弧。
●要分清推论1的题设和结论,即已知什么条件,可推出什么结论. 这是正确理解应用推论1的关键;
●例3是基本几何作图,会通过作弧所夹弦
的垂直平分线来等分弧.能够体会转化思想
在这里的运用.回味引伸
垂径定理及其推论1的实质是把(1)直线MN过圆心;
(2)直线MN垂直AB; (3)直线MN平分AB;
(4)直线MN平分弧AMB; (5)直线MN平分弧ANB
中的两个条件进行了四种组合,分别推出了其余的三个
结论.这样的组合还有六种,由于时间有限,课堂上未作
进一步的推导,同学们课下不妨试一试. MOABNCD证明: 由AB∥CD可得:弧AC=弧BDMN是AB的垂直平分线 则有:MN过圆心O是直径弧AM=弧BM∴MN垂直平分CD∴ 弧AM-弧AC =弧BM-弧BD
即 弧CM=弧DM
布置作业:
习题P52 3-5.谢 谢 !
④弧AM=弧BM
⑤弧AN=弧BN垂径定理: 如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线MN过圆心O ② MN⊥AB③AC=BC
④弧AM=弧BM
⑤弧AN=弧BN垂径定理: 课题:垂直于弦的直径(2)垂径定理的推论
MOACBN①直线MN过圆心③ AC=BC
②MN⊥AB
④弧AM=弧BM ⑤弧AN=弧BN探索一:结论:推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。OABMN一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。CDMOACBN② MN⊥AB ③ AC=BC
①直线MN过圆心O
④弧AM=弧BM
⑤弧AN=弧BN探索二:推论1: (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;MOACBN② MN⊥AB ③ AC=BC ④弧AM=弧BM①直线MN过圆心O
⑤弧AN=弧BN探索三:推论1: (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
推论1:
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;.
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
推论2. 圆的两条平行弦所夹的弧相等。
推论2. 圆的两条平行弦所夹的弧相等。
MOABNCD作直径MN垂直于弦AB∵AB∥CD ∴直径MN也垂直于弦CD于是 弧AM=弧BM, 弧CM=弧DM∴弧AM-弧CM =弧BM-弧DM 即 弧AC=弧BDCDABE例:平分已知弧AB已知:弧AB
作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点CDABEFG变式一: 求弧AB的四等分点。 mnCDABMTEFGHNP错在哪里?等分弧时一定要作弧所夹弦的垂直平分线。●作AB的垂直平分线CD。●作AT.BT的垂直
平分线EF.GHCABE变式二:你能确定 弧AB的圆心吗?mnDCABEmnO你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据: 已知:AB、CD是⊙O的两条平行弦,
MN是AB的垂直平分线。
求证:MN垂直平分CD。 MOANCDB 圆内平行弦的垂直平分线是互相重合的。 已知:AB、CD是⊙O的两条平行弦,
MN是AB的垂直平分线。
求证:MN垂直平分CD。 MOABNCD分析:MN是AB的垂直平分线 则有: MN过圆心O是直径由AB∥CD, MN⊥AB 则有:MN⊥CD由垂径定理,得MN平分CD所以:MN垂直平分CDMOBNCD证明: ∵ MN是AB的垂直平分线 ∴ MN过圆心是直径∴MN⊥CD∴ MN平分CDA∵AB∥CD,MN⊥AB
∴MN垂直平分CD
课堂小结:
本节课探索发现了垂径定理的推论1和推
论2,并且运用推论1等分弧。
●要分清推论1的题设和结论,即已知什么条件,可推出什么结论. 这是正确理解应用推论1的关键;
●例3是基本几何作图,会通过作弧所夹弦
的垂直平分线来等分弧.能够体会转化思想
在这里的运用.回味引伸
垂径定理及其推论1的实质是把(1)直线MN过圆心;
(2)直线MN垂直AB; (3)直线MN平分AB;
(4)直线MN平分弧AMB; (5)直线MN平分弧ANB
中的两个条件进行了四种组合,分别推出了其余的三个
结论.这样的组合还有六种,由于时间有限,课堂上未作
进一步的推导,同学们课下不妨试一试. MOABNCD证明: 由AB∥CD可得:弧AC=弧BDMN是AB的垂直平分线 则有:MN过圆心O是直径弧AM=弧BM∴MN垂直平分CD∴ 弧AM-弧AC =弧BM-弧BD
即 弧CM=弧DM
布置作业:
习题P52 3-5.谢 谢 !
