北师大版九年级数学上册试题 1.3 正方形的性质与判定北师大版(含答案)
文档属性
| 名称 | 北师大版九年级数学上册试题 1.3 正方形的性质与判定北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 827.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 00:00:00 | ||
图片预览



文档简介
1.3 正方形的性质与判定
一、单选题
1.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
2.如图,已知正方形ABCD的边长为5,E为BC边上的一点,∠EBC=30°,则BE的长为 ( )
A.cm B.2cm C.5 cm D.10 cm
3.在四边形ABCD中,∠A=∠B=∠C=90°,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
4.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A. B. C. D.
5.如图,菱形ABCD中,,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B.15 C.16 D.17
6.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是 ( )
A.1 B.1.5 C.2 D.2.5
7.如图,边长分别为和的两个正方形和并排放在一起,连接并延长交于点,交于点,则
A. B. C.2 D.1
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1-S2+S3+S4等于( )
A.4 B.6 C.8 D.10
9.下列命题中正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形;
B.对角线互相垂直且平分的四边形是菱形;
C.一个角为90°且一组邻边相等的四边形是正方形;
D.对角线相等的四边形是矩形
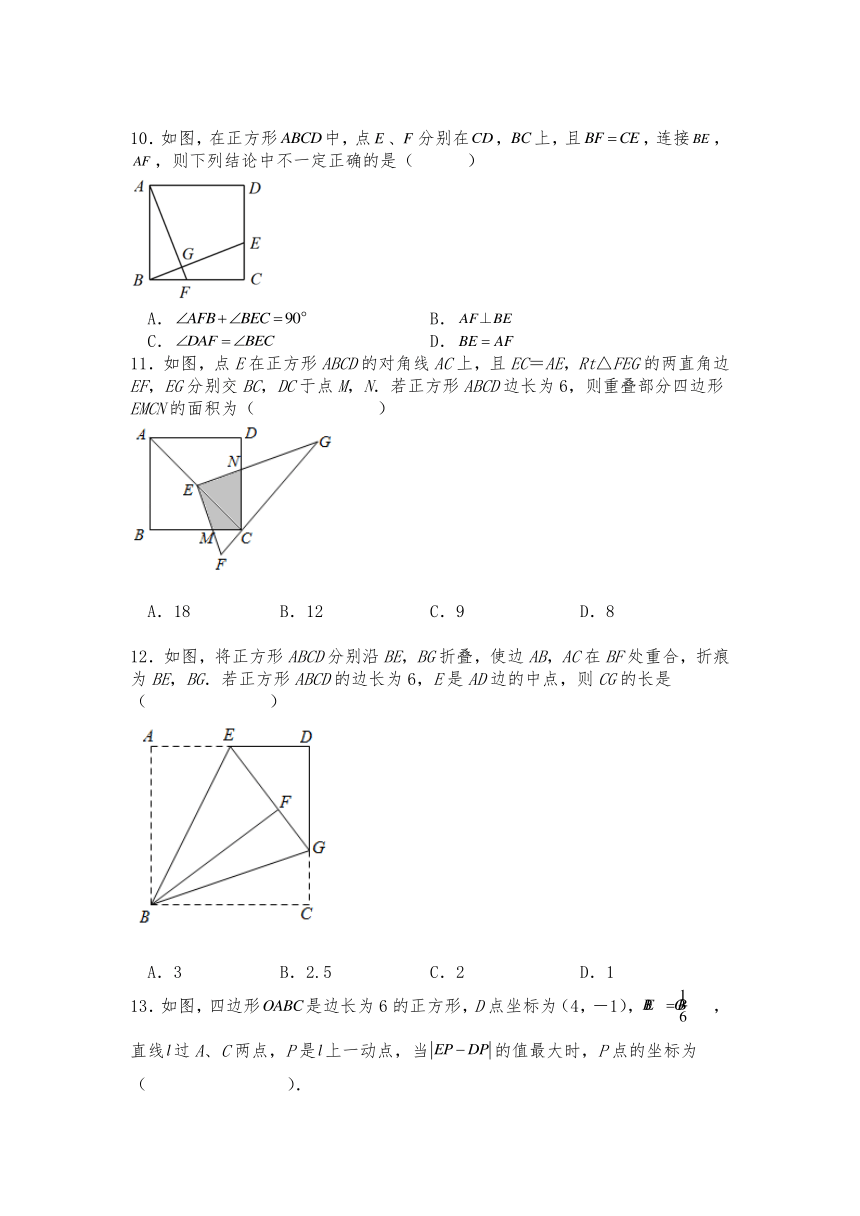
10.如图,在正方形中,点、分别在,上,且,连接,,则下列结论中不一定正确的是( )
A. B.
C. D.
11.如图,点E在正方形ABCD的对角线AC上,且EC=AE,Rt△FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD边长为6,则重叠部分四边形EMCN的面积为( )
A.18 B.12 C.9 D.8
12.如图,将正方形ABCD分别沿BE,BG折叠,使边AB,AC在BF处重合,折痕为BE,BG.若正方形ABCD的边长为6,E是AD边的中点,则CG的长是( )
A.3 B.2.5 C.2 D.1
13.如图,四边形是边长为6的正方形,D点坐标为(4,-1),,直线过A、C两点,P是上一动点,当的值最大时,P点的坐标为( ).
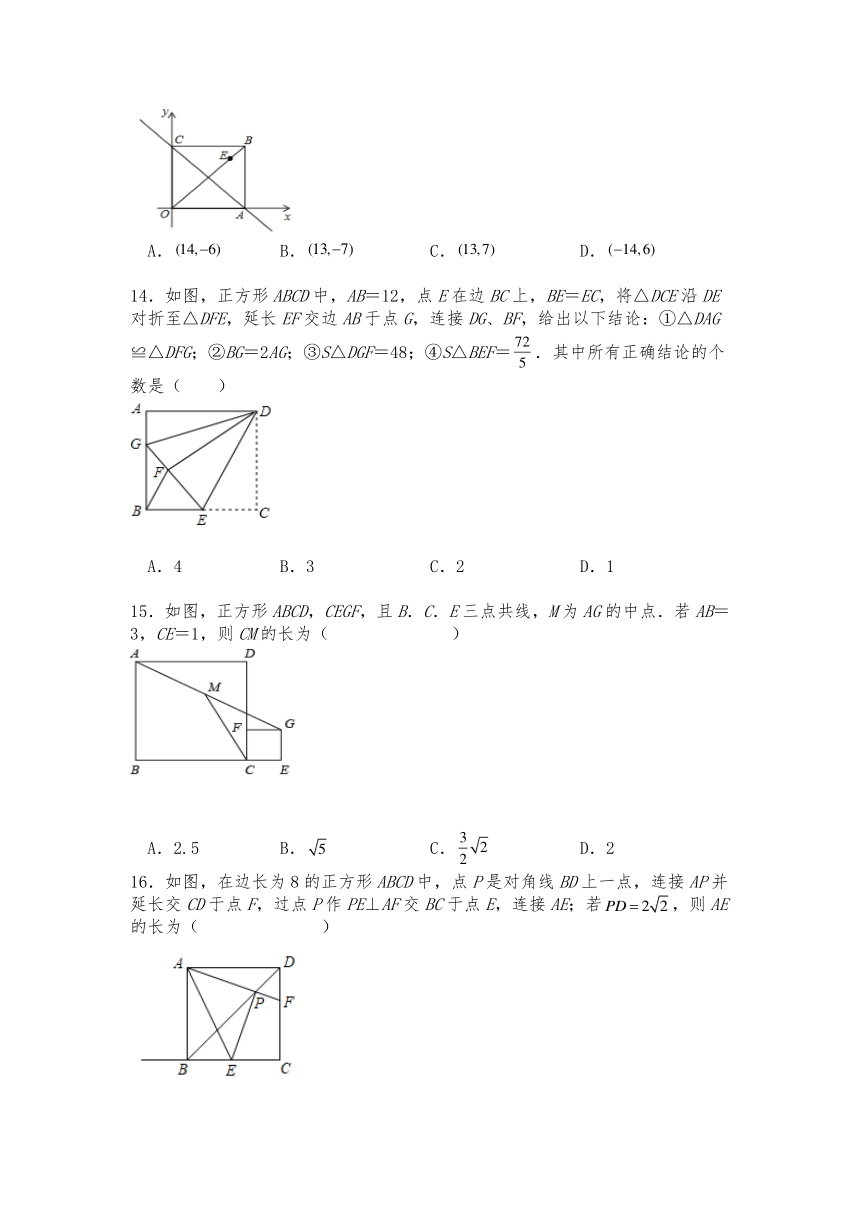
A. B. C. D.
14.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=48;④S△BEF=.其中所有正确结论的个数是( )
A.4 B.3 C.2 D.1
15.如图,正方形ABCD,CEGF,且B.C.E三点共线,M为AG的中点.若AB=3,CE=1,则CM的长为( )
A.2.5 B. C. D.2
16.如图,在边长为8的正方形ABCD中,点P是对角线BD上一点,连接AP并延长交CD于点F,过点P作PE⊥AF交BC于点E,连接AE;若,则AE的长为( )
A.10 B. C. D.
二、填空题
1.若正方形的边长为a,则它的对角线长为__________.
2.如图所示,已知四边形ABCD是菱形,则只需补充条件:________(用字母表示)就可以判定四边形ABCD是正方形.(填一个即可)
3.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是___________.
4.在中,已知、为对角线,现有以下四个条件:①;② ;③;④.从中选取两个条件,可以判定为正方形的是_________.(写出一组即可)
5.如图,E是正方形ABCD的对角线BD上一点,连接CE,过点E作,垂足为点F.若,,则正方形ABCD的面积为___.
6.作正方形中对角线的平行线,点E在直线上,且四边形是菱形,则 _______.
7.如图,在△ABC中,∠C=90°,AC=4,BC=2,以AB为一条边向三角形外部作正方形ABDE,P为DE上一点,则四边形ACBP的面积为_____.
8.如图,正方形的边长为,点是中点,将沿翻折至,延长交边于点,则的长为______.
9.如图,四边形ABCD是边长为5的正方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 _____.
10.如图,在正方形 ABCD 中,AC 为对角线,E 为 AC 上一点,连接 EB、ED,延长 BE交 AD 于 F.当∠BED=120°时,则∠ABF 的度数为__________°.
11.如图,C为AB上任意一点,分别以AC、BC为边在AB同侧作正方形ACDE、正方形BCFG,设∠AFC=α,则∠BDC为_________(用含α的代数式表示).
12.如图,正方形ABCD的边长为15,P为BC边上一点,PB=2PC,把△PAB沿PA边翻折,点B落在B1处,设PB1的延长线交CD于Q,则PQ=_______.
13.如图,已知正方形的边长为1,点是边的中点,将沿直线翻折,使得点落在同一平面内的点处,联结并延长交射线于点,那么的长为______.
三、解答题
1.如图,若四边形的对角线与相交于点O,且,则四边形是正方形吗?
2.如图,在正方形ABCD中,,,,图中有几个直角三角形?你是如何判断的?与同伴进行交流.
3.如图,M、N分别是正方形的边的中点,与交于点P,连结,求证:.
4.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
5.如图,正方形ABCD中,.
(1)求证:;
(2)求证:;
(3)若,且,则_______.
6.如图,在正方形的外侧,作等边角形,连接、.
(1)求证:;
(2)求的度数.
7.综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
答案
一、单选题
D.D.A.D.C.C.B.B.B.A.C.C.B.B.B.C.
二、填空题
1.
2.答案不唯一,如∠ABC=90°或AC=BD等
3.22.5°.
4.①③或①④或②③或②④.
5.196.
6.或
7.14
8..
9..
10.15.
11.90°-α.
12.13
13..
三、解答题
1.
解:四边形ABCD是正方形,
理由是:∵OA=OB=OC=OD,
∴AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
∵,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形.
2.图中,,分别有一个角为正方形的内角,是直角;
是正方形,
,
,
,,
也是直角三角形
故图中共有个直角三角形.
3.证明:延长交于Q,
在正方形中,AD=DC=CB,∠D=∠NCB=90°,
∵M、N分别是正方形的边的中点,
∴DM=AM=,CN=
∴DM=CN,
在△DMC和△CNB中,
,
∴△DMC≌△CNB(SAS),
∴∠DCM=∠CBN,
∵∠DCM+∠PCB=90°
∴∠CBP+∠PCB=∠DCM+∠PCB=90°,
∴∠BPC=180°-∠PCB-∠CBP=180°-(∠PCB+∠CBP)=90°
在△CDM和△QAM中
,
∴△CDM≌△QAM(AAS),
∴CD=QA,
在Rt△QBP中,AP为斜边中线,
∴AP==AB.
4.解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
5.(1)
证明:∵四边形ABCD是正方形,
∴,
∵,
∴,
∴(SAS);
(2)
证明:由(1)可知,
∴,
∵,
∴,即,
∴;
(3)
解:连接DE,如图所示:
由(2)可知,
∵,
∴由勾股定理得:,
∵AD=DC=AB=6,
∴在Rt△ADE中,由勾股定理得:,
∴;
故答案为:.
6.解:(1)证明:∵四边形ABCD是正方形,
∴AB=CD,且∠BAD=∠CDA=90°,
∵△ADE是等边三角形,
∴AE=DE,且∠EAD=∠EDA=60°,
∴∠BAE=∠BAD+∠EAD=150°,∠CDE=∠CDA+∠EDA=150°,
∴∠BAE=∠CDE,
在△BAE和△CDE中:
,
∴.
(2)∵AB=AD,且AD=AE,
∴△ABE为等腰三角形,
∴∠ABE=∠AEB,
又∠BAE=150°,
∴由三角形内角和定理可知:
∠AEB=(180°-150°)÷2=15°.
故答案为:15°.
7.(1)
解:
(2)
∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°
∴BM=BC
①
∴
∴∠MBQ=∠CBQ
②
(3)
当点Q在点F的下方时,如图,
,DQ=DF+FQ=4+1=5(cm)
由(2)可知,
设
,
即
解得:
∴;
当当点Q在点F的上方时,如图,
cm,DQ =3cm,
由(2)可知,
设
,
即
解得:
∴.
一、单选题
1.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
2.如图,已知正方形ABCD的边长为5,E为BC边上的一点,∠EBC=30°,则BE的长为 ( )
A.cm B.2cm C.5 cm D.10 cm
3.在四边形ABCD中,∠A=∠B=∠C=90°,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )
A.BC=CD B.AB=CD C.∠D=90° D.AD=BC
4.如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A. B. C. D.
5.如图,菱形ABCD中,,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B.15 C.16 D.17
6.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是 ( )
A.1 B.1.5 C.2 D.2.5
7.如图,边长分别为和的两个正方形和并排放在一起,连接并延长交于点,交于点,则
A. B. C.2 D.1
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1-S2+S3+S4等于( )
A.4 B.6 C.8 D.10
9.下列命题中正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形;
B.对角线互相垂直且平分的四边形是菱形;
C.一个角为90°且一组邻边相等的四边形是正方形;
D.对角线相等的四边形是矩形
10.如图,在正方形中,点、分别在,上,且,连接,,则下列结论中不一定正确的是( )
A. B.
C. D.
11.如图,点E在正方形ABCD的对角线AC上,且EC=AE,Rt△FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD边长为6,则重叠部分四边形EMCN的面积为( )
A.18 B.12 C.9 D.8
12.如图,将正方形ABCD分别沿BE,BG折叠,使边AB,AC在BF处重合,折痕为BE,BG.若正方形ABCD的边长为6,E是AD边的中点,则CG的长是( )
A.3 B.2.5 C.2 D.1
13.如图,四边形是边长为6的正方形,D点坐标为(4,-1),,直线过A、C两点,P是上一动点,当的值最大时,P点的坐标为( ).
A. B. C. D.
14.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=48;④S△BEF=.其中所有正确结论的个数是( )
A.4 B.3 C.2 D.1
15.如图,正方形ABCD,CEGF,且B.C.E三点共线,M为AG的中点.若AB=3,CE=1,则CM的长为( )
A.2.5 B. C. D.2
16.如图,在边长为8的正方形ABCD中,点P是对角线BD上一点,连接AP并延长交CD于点F,过点P作PE⊥AF交BC于点E,连接AE;若,则AE的长为( )
A.10 B. C. D.
二、填空题
1.若正方形的边长为a,则它的对角线长为__________.
2.如图所示,已知四边形ABCD是菱形,则只需补充条件:________(用字母表示)就可以判定四边形ABCD是正方形.(填一个即可)
3.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是___________.
4.在中,已知、为对角线,现有以下四个条件:①;② ;③;④.从中选取两个条件,可以判定为正方形的是_________.(写出一组即可)
5.如图,E是正方形ABCD的对角线BD上一点,连接CE,过点E作,垂足为点F.若,,则正方形ABCD的面积为___.
6.作正方形中对角线的平行线,点E在直线上,且四边形是菱形,则 _______.
7.如图,在△ABC中,∠C=90°,AC=4,BC=2,以AB为一条边向三角形外部作正方形ABDE,P为DE上一点,则四边形ACBP的面积为_____.
8.如图,正方形的边长为,点是中点,将沿翻折至,延长交边于点,则的长为______.
9.如图,四边形ABCD是边长为5的正方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 _____.
10.如图,在正方形 ABCD 中,AC 为对角线,E 为 AC 上一点,连接 EB、ED,延长 BE交 AD 于 F.当∠BED=120°时,则∠ABF 的度数为__________°.
11.如图,C为AB上任意一点,分别以AC、BC为边在AB同侧作正方形ACDE、正方形BCFG,设∠AFC=α,则∠BDC为_________(用含α的代数式表示).
12.如图,正方形ABCD的边长为15,P为BC边上一点,PB=2PC,把△PAB沿PA边翻折,点B落在B1处,设PB1的延长线交CD于Q,则PQ=_______.
13.如图,已知正方形的边长为1,点是边的中点,将沿直线翻折,使得点落在同一平面内的点处,联结并延长交射线于点,那么的长为______.
三、解答题
1.如图,若四边形的对角线与相交于点O,且,则四边形是正方形吗?
2.如图,在正方形ABCD中,,,,图中有几个直角三角形?你是如何判断的?与同伴进行交流.
3.如图,M、N分别是正方形的边的中点,与交于点P,连结,求证:.
4.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
5.如图,正方形ABCD中,.
(1)求证:;
(2)求证:;
(3)若,且,则_______.
6.如图,在正方形的外侧,作等边角形,连接、.
(1)求证:;
(2)求的度数.
7.综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
答案
一、单选题
D.D.A.D.C.C.B.B.B.A.C.C.B.B.B.C.
二、填空题
1.
2.答案不唯一,如∠ABC=90°或AC=BD等
3.22.5°.
4.①③或①④或②③或②④.
5.196.
6.或
7.14
8..
9..
10.15.
11.90°-α.
12.13
13..
三、解答题
1.
解:四边形ABCD是正方形,
理由是:∵OA=OB=OC=OD,
∴AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
∵,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形.
2.图中,,分别有一个角为正方形的内角,是直角;
是正方形,
,
,
,,
也是直角三角形
故图中共有个直角三角形.
3.证明:延长交于Q,
在正方形中,AD=DC=CB,∠D=∠NCB=90°,
∵M、N分别是正方形的边的中点,
∴DM=AM=,CN=
∴DM=CN,
在△DMC和△CNB中,
,
∴△DMC≌△CNB(SAS),
∴∠DCM=∠CBN,
∵∠DCM+∠PCB=90°
∴∠CBP+∠PCB=∠DCM+∠PCB=90°,
∴∠BPC=180°-∠PCB-∠CBP=180°-(∠PCB+∠CBP)=90°
在△CDM和△QAM中
,
∴△CDM≌△QAM(AAS),
∴CD=QA,
在Rt△QBP中,AP为斜边中线,
∴AP==AB.
4.解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
5.(1)
证明:∵四边形ABCD是正方形,
∴,
∵,
∴,
∴(SAS);
(2)
证明:由(1)可知,
∴,
∵,
∴,即,
∴;
(3)
解:连接DE,如图所示:
由(2)可知,
∵,
∴由勾股定理得:,
∵AD=DC=AB=6,
∴在Rt△ADE中,由勾股定理得:,
∴;
故答案为:.
6.解:(1)证明:∵四边形ABCD是正方形,
∴AB=CD,且∠BAD=∠CDA=90°,
∵△ADE是等边三角形,
∴AE=DE,且∠EAD=∠EDA=60°,
∴∠BAE=∠BAD+∠EAD=150°,∠CDE=∠CDA+∠EDA=150°,
∴∠BAE=∠CDE,
在△BAE和△CDE中:
,
∴.
(2)∵AB=AD,且AD=AE,
∴△ABE为等腰三角形,
∴∠ABE=∠AEB,
又∠BAE=150°,
∴由三角形内角和定理可知:
∠AEB=(180°-150°)÷2=15°.
故答案为:15°.
7.(1)
解:
(2)
∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°
∴BM=BC
①
∴
∴∠MBQ=∠CBQ
②
(3)
当点Q在点F的下方时,如图,
,DQ=DF+FQ=4+1=5(cm)
由(2)可知,
设
,
即
解得:
∴;
当当点Q在点F的上方时,如图,
cm,DQ =3cm,
由(2)可知,
设
,
即
解得:
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
