北师大版九年级数学上册试题4.5 相似三角形动态几何,坐标问题(含答案)
文档属性
| 名称 | 北师大版九年级数学上册试题4.5 相似三角形动态几何,坐标问题(含答案) | 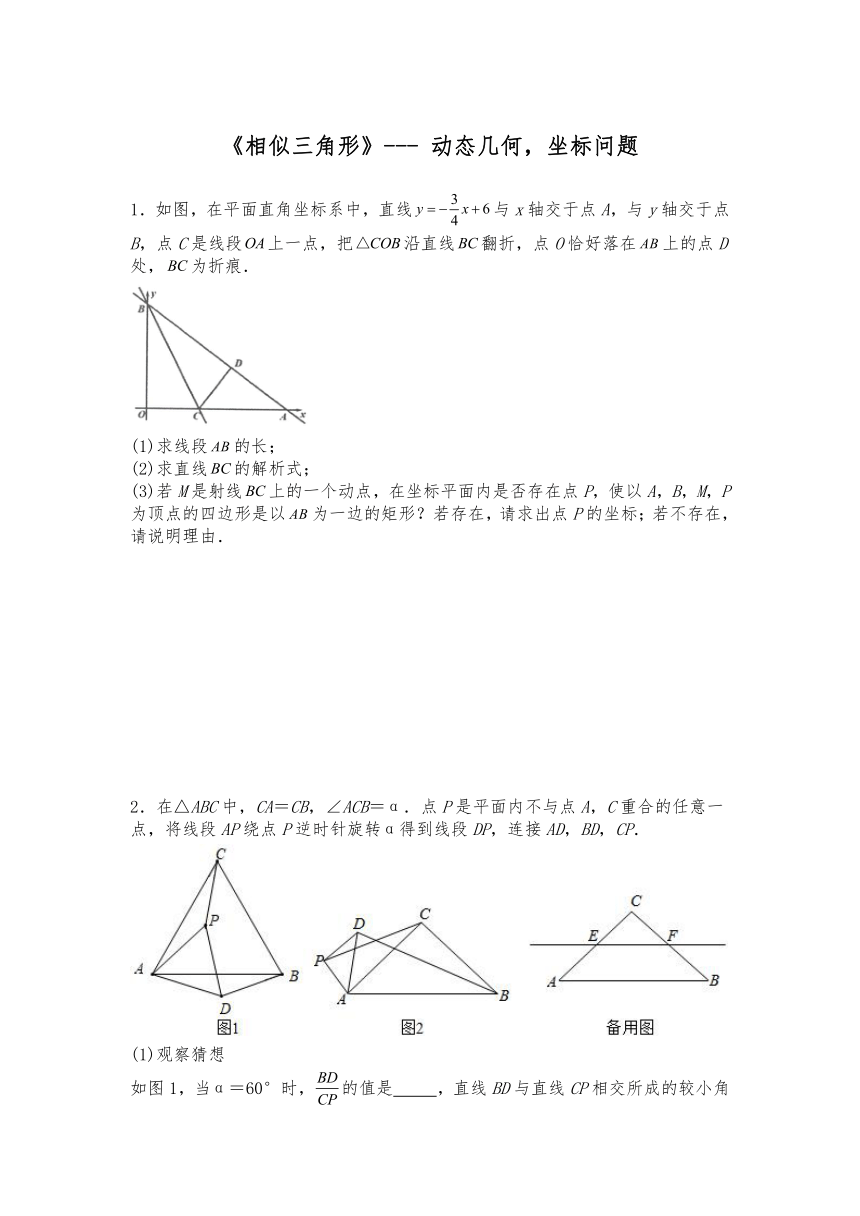 | |
| 格式 | docx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 22:15:27 | ||
图片预览



文档简介
《相似三角形》--- 动态几何,坐标问题
1.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,点C是线段上一点,把沿直线翻折,点O恰好落在上的点D处,为折痕.
(1)求线段的长;
(2)求直线的解析式;
(3)若M是射线上的一个动点,在坐标平面内是否存在点P,使以A,B,M,P为顶点的四边形是以为一边的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
2.在△ABC中,CA=CB,∠ACB=α.点P是平面内不与点A,C重合的任意一点,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当α=60°时,的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当α=90°时,请写出,并就图2的情形说明理由.
(3)解决问题
当α=90°时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时的值.
3.问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,∠B=∠A=∠EDF.
(1)初步尝试:如图①,当△ABC是等边三角形,判断:△ADM △BND(填相似或全等);
(2)类比探究:如图②,当AC=BC时,上述结论是否还成立?请说明理由.
(3)延伸拓展:如图③,在(2)的条件下,当点D在BA的延长线上运动到点M与点C重合时,若S△ADM:S△BND=1:2,BN:BM=1:3,AD=1,则DN= .
4.
(1)[基础巩固]如图①,在三角形纸片ABC中,,将折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为______;
(2)[思维提高]如图②,在三角形纸片ABC中,,,将折叠,使点B与点C重合,折痕为MN,求的值;
(3)[拓展延伸]如图③,在三角形纸片ABC中,,,,将沿过顶点C的直线折叠,使点B落在边AC上的点处,折痕为CM.求线段AC的长;
5.直线y=2x+4与x轴交于点A,与y轴交于点B,点C在x轴的正半轴上,△ABC面积为10.
(1)直接写出点C的坐标;
(2)如图1,F为线段AB的中点,点G在y轴上,以FG为边,向右作正方形FGQP,点Q落在直线BC上,求点G的坐标;
(3)如图2,M在射线BA上,点N在射线BC上,直线MN交y轴于H点,若HB=HM,求的值.
6.如图1,在矩形ABCD中,,,点E在AB边上,且.点F是BC边上的动点.将沿EF折叠得到.直线GF与直线AB的交点为H.
(1)如图2,点F与点C重合时,求与的面积比;
(2)如图3,当H在点A的上方,且满足三角形HEF是等腰三角形时,求线段EH的长.
(3)在点F的运动过程中,以E、G、H为顶点的三角形能否与以B、C、D为顶点的三角形相似?若能,求BF的长;若不存在,请说明理由.
7.已知:在平面直角坐标系xOy中,直线过点A(-1,0)、C(2,3)两点.
(1)如图1,求直线的解析式;
(2)如图2,过点C作轴于点B,点E是射线BC上一点,连接AE,过点E作,且.连接FC交x轴于点G,延长FE交直线AC于点P,连接PG,设点P的横坐标为t,△PAG的面积为S,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点P作轴于点H,过点F作交PH延长线于点K.若,求点K坐标.
8.如图1,在中,于点D,在DA上取点E,使,连接BE、CE.
(1)直接写出CE与AB的位置关系;
(2)如图2,将绕点D旋转,得到(点,分别与点B,E对应),连接,在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致 请说明理由;
(3)如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若,求的长.
9.综合与实践:
数学活动课上,老师让同学们根据下面情境提出问题并解答.
问题情境:在中,点P是边上一点.将沿直线折叠,点D的对应点为E.
“兴趣小组”提出的问题是:如图1,若点P与点A重合,过点E作,与交于点F,连接,则四边形是菱形.
(1)数学思考:请你证明“兴趣小组”提出的问题;
(2)拓展探究:“智慧小组”提出的问题是:如图2,当点P为的中点时,延长交于点F,连接.试判断与的位置关系,并说明理由.
请你帮助他们解决此问题.
(3)问题解决:“创新小组”在前两个小组的启发下,提出的问题是:如图3,当点E恰好落在边上时,,,.则的长为___________.(直接写出结果)
10.已知中,点、分别在边、上,且,将绕点逆时针旋转.设旋转角为
(1)试说明;
(2)若,,当时,若点恰好落在边中点处,求的值;
(3)若,,当点恰好落在边上时,延长交于,若,求的值.
11.如图1,在四边形ABCD中,,,.
(1)求∠ACD的度数;
(2)如图2,F为线段CD的中点,连接BF,求证:;
(3)如图3,若,线段BC上有一动点M,连接OM,将沿OM所在直线翻折至的位置,P为B的对应点,连接PA,PC,当的值最小时,设O到直线PC的距离为,PC的长度为,直接写出的值.
12.(1)【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
(2)【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(3)【拓展应用】如图③,在菱形中,为边上的三等分点,将沿翻折得到,直线交于点求的长.
13.小亮在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在中,于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,且.若,,则正方形PQMN的边长等于______.
(2)操作:能画出这类正方形吗?小亮按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画,在AB上任取一点,画正方形,使,在BC边上,在内,连结并延长交AC于点N,画于点M,交AB于点P,于点Q,得到四边形PQMN.
(3)推理:如图3,若点E是BN的中点,求证:.
(4)拓展:在(2)的条件下,射线BN上截取,连结EQ,EM(如图4).当时,猜想的度数,并尝试证明.
请帮助小亮解决“温故”、“推理”、“拓展”中的问题.
14.矩形AOBC在平面直角坐标系中的位置如图所示,点A在x轴的负半轴上,点B在y轴的正半轴上,连接AB,将△ABC沿AB折叠得△ABE,AE交y轴于点D,线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD.
(1)请直接写出点A的坐标为________,点D的坐标为________;
(2)点P为直线AB上一点,连接PO、PD,当△POD的周长最小时,求点P的坐标;
(3)点M在x轴上,点N在直线AB上,坐标平面内是否在点Q,使以B、M、N、Q为顶点的四边形为正方形 若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
15.问题情境:如图1所示,在△ABC中,D、E分别是AB、AC上的点,DEBC,在图1中将ADE绕A点顺时针旋转一定角度,得到图2,然后将BD、CE分别延长至M、N,使DM=BD,EN=CE,得到图3,请解答下列问题:
(1)猜想证明:若AB=AC,请探究下列数量关系:
①在图2中,BD与CE的数量关系是_________.
②在图3中,猜想∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)拓展应用:其他条件不变,若AB=AC,按上述操作方法,得到图4,请你继续探究:∠MAN与∠BAC的数量关系?AM与AN的数量关系?直接写出你的猜想.
16.如图,矩形中,,,点是的中点,是射线上一点,延长交直线于,过作,分别交射线、直线于、.
(1)①当时,______;
②点在上取不同位置,的值是否变化?若不变,求出它的值,若改变,请说明理由;
(2)连接,当是等腰直角三角形时,求的长;
(3)直接写出的最小值______.
答案
1.(1)
解:令x=0,则y=6,
∴B(0,6),
令y=0,则x=8,
∴A(8,0),
∴AB=10;
(2)
解:由折叠的性质可知,OC=CD,OB=CD,
∵OB=6,
∴BD=6,
∵AB=10,
∴AD=4,
在Rt△ACD中,AC2=CD2+AD2,
∴(8OC)2=CO2+42,
∴CO=3,
∴C(3,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴y=2x+6;
(3)
解:存在点P,使以A,B,M,P为顶点的四边形是以AB为一边的矩形,理由如下:
设M(t,-2t+6),(t>0),P(x,y),
当以AB为矩形的一边时,BM为矩形的对角线,
∴,
过点M作EF∥x轴,过点A作AF⊥EF交于F,过点P作PE⊥EF交于点E,
∵∠AMP=90°,
∴∠PME+∠AMF=90°,
∵∠AMF+∠MAF=90°,
∴∠AMF=∠PME,
∴△AMF∽△MPE,
∴,
∵AF=2t-6,MF=8-t,PE=y+2t-6,EM=t-x,
∴,
∴,
解得t=5,
∴x=3,y=2,
∴P(3,2).
2.
(1)解:如图1中,延长CP交BD的延长线于E.∵CA=CB,∠ACB=60°,∴ CAB为等边三角形,又∵将线段AP绕点P逆时针旋转60°得到线段DP∴AP=DP,∠APD=60°∴ APD为等边三角形,∴CA=BA,PA=DA,∴∠PAD=∠CAB=60°,∴∠PAD-∠PAB=∠CAB-∠PAB∴∠CAP=∠BAD,∵CA=BA,PA=DA,∴△CAP≌△BAD(SAS),∴PC=BD,∠ACP=∠ABD,∵∠AOC=∠BOE,∴∠BEO=∠CAO=60°,∴=1,故答案为1,60°.
(2)=,理由:如图2中,设BD交AC于点O.
∵∠PAD=∠CAB=45°,∴∠PAC=∠DAB,∵==,∴△DAB∽△PAC,∴∠PCA=∠DBA, ==,
如图3﹣1中,当点D在线段PC上时.
∵CE=EA,CF=FB,∴EF∥AB,∴∠EFC=∠ABC=45°,∵∠PAO=45°,∴∠PAO=∠OFH,∵∠POA=∠FOH,∴∠H=∠APO,∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA,∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°,∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,PD=a,∴=.
解法二:在Rt△PAD中,∵E是AC的中点,∴PE=EA=EC,∴∠EPC=∠ECP,∵∠CEF=45°=∠EPC+∠ECP,∴∠EPC=∠ECP=22.5°,∵∠PDA=45°=∠ACD+∠DAC,∴∠DAC=22.5°,∴AD=DC,设PD=a,则AD=DC=a,∴,如图3﹣3中,当点P在线段CD上时,同理可得DA=DC,
设AD=a,PD=a,∴PC=a﹣a,∴.
3.
(1)解:如图①,∵△ABC是等边三角形,∠B=∠A=∠EDF,∴∠B=∠A=∠EDF=60°,∴∠AMD=180°﹣60°﹣∠ADM=120°﹣∠ADM,∠BDN=180°﹣60°﹣∠ADM=120°﹣∠ADM,∴∠AMD=∠BDN,∴△ADM∽△BND,故答案为:相似.
(2)解:成立,如图②,∵AC=BC,∴∠B=∠A,∴∠B=∠A=∠EDF,设∠B=∠A=∠EDF=x,∵∠AMD=180°﹣∠A﹣∠ADM=180°﹣x﹣∠ADM,∠BDN=180°﹣∠EDF﹣∠ADM=180°﹣x﹣∠ADM,∴∠AMD=∠BDN,∴△ADM∽△BND.
(3)解:如图③,作CG⊥AB于点G,设S△CDN=m,则∠CGD=∠CGB=90°,设∠CBA=∠CAB=∠EDF=x,∵∠DCA=∠CAB﹣∠CDB=x﹣∠CDB,∠NDB=∠EDF﹣∠CDB=x﹣∠CDB,∴∠DCA=∠NDB;∵∠CAD=180°﹣∠CAB=180°﹣x,∠DBN=180°﹣∠CBA=180°﹣x,∴∠CAD=∠DBN,∴△ADC∽△BND,∴;∵点M与点C重合,S△ADM:S△BND=1:2,BN:BM=1:3,∴S△ADC:S△BND=1:2,BN:BC=1:3,∴S△BND=S△CDN=,∴S△ADC=S△BND=,∴S△ABC=m﹣﹣m=m,∴,∵AD=1,∴AB=5AD=5,∵AC=BC,∴AG=BG=AB=,∴DG=;∵,∴,∴DN=CD,BN=AD=,∴BC=3BN=,∴CG2=BC2﹣BG2=,∴CD=,∴DN=,故答案为: .
4.
(1)解:如图①中,∵△ABC折叠,使点B与点C重合,折痕为MN,∴MN垂直平分线段BC,∴CN=BN,∵∠MNB=∠ACB=90°,∴MN∥AC,∵CN=BN,∴AM=BM.故答案为AM=BM.
(2)如图②中,∵CA=CB=6,∴∠A=∠B,由题意MN垂直平分线段BC,∴BM=CM,∴∠B=∠MCB,∴∠BCM=∠A,∵∠B=∠B,∴△BCM∽△BAC,∴,∴,∴,∴,∴.
(3)如图③中,由折叠的性质可知,
CB=CB′=6,∠BCM=∠ACM,∵∠ACB=2∠A,∴∠BCM=∠A,∵∠B=∠B,∴△BCM∽△BAC,∴∴,∴BM=4,∴AM=CM=5,∴,∴.
5.(1)
解:∵直线y=2x+4与x轴交于点A,与y轴交于点B,
令y=0,y=﹣2,令x=0,x=4,
∴A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∵,
∴AC=5,
∴OC=3,
∴C(3,0),
(2)
解:设直线BC的解析式为:y=kx+b,把B(0,4),C(3,0),代入得:
,解得: ,
∴直线BC的解析式为:;
由(1)知:A(﹣2,0),B(0,4),
∵F为线段AB的中点,
∴F(-1,2),
设G(0,n),
①当n>2时,如图,
点Q落在BC上时,过G作直线MN平行于x轴,过点F,Q作该直线MN的垂线,垂足分别为M,N,
∵四边形FGQP是正方形,
∴∠FGQ=90°,FG=QG,
∴∠FGM=90°﹣∠NGQ=∠GQN,
而∠FMG=∠GNQ=90°,
∴△FMG≌△GNQ(AAS),
∴MG=NQ=1,FM=GN=n﹣2,
∴Q(n﹣2,n﹣1),
∴Q在直线上,
∴n﹣1=+4,
∴n=,
∴G(0,);
①当n<2时,如图,
点Q落在BC上时,过G作直线MN平行于x轴,过点F,Q作该直线MN的垂线,垂足分别为M,N.
∵四边形FGQP是正方形,
∴∠FGQ=90°,FG=QG,
∴∠FGM=90°﹣∠NGQ=∠GQN,
∵∠FMG=∠GNQ=90°,
∴△FMG≌△GNQ(AAS),
∴MG=NQ=1,FM=GN=2﹣n,
∴Q(2﹣n,n+1),
∴Q在直线上,
∴n+1=+4,
∴n=﹣1,
∴G(0,﹣1);
综上所述,满足条件的点G坐标为(0,)或(0,﹣1);
(3)
解:过点M作MP∥x轴交BC于点P,交y轴于Q,
∵B(0,4),C(3,0),A(﹣2,0),
∴AC=5,OB=4,OC=3,
在Rt△BOC中,
由勾股定理得:BC=,
∴AC=BC=5,
∴∠ABC=∠BAC,
∵MP∥x轴,
∴∠BMP=∠BAC,∠AOB=∠MQH=90°,
∴∠BMP=∠ABC,
∵HM=HB,
∴∠HBM=∠HMB,
∴∠ABC﹣∠HBM=∠BMP﹣∠HMB,
即∠HBN=∠HMQ,
∴∠MHQ≌△BHN(ASA),
∴∠MNB=∠MQH=∠BOC=90°,
∵∠OBC=∠OBC,
∴△BHN∽△BCO,
∴,
∴.
6.(1)如图,∵∠GHE=∠BHC,∠EGH=∠CBH,∴△HEG∽△HCB,根据面积之比等于相似比的平方,∴,∵EG=BE=AB-AE=2,∴..
(2)根据题意,EF=EH,根据折叠性质,等腰三角形三线合一性质,得FB=FG=GH,∴∠BHF=30°,∵EG=BE=AB-AE=2,∴EH=4.
(3)∵ BC=5,DC=3,四边形ABCD是矩形,∴BD==.根据题意,得到CH⊥BD时,△HEG∽△BCD,∴ ,∴ ,解得
.∵△HEG∽△HFB,∴△HFB∽△BDC,∴ ,∴ ,解得.当H在下方时,∵ BC=5,DC=3,四边形ABCD是矩形,∴BD==.根据题意,得到CH⊥BD时,△HEG∽△BCD,∴ ,∴ ,解得,∴.∵△HEG∽△HFB,∴△HFB∽△BDC,∴ ,∴ ,解得.
7.(1)
设直线AC的解析式为y=kx+b,
,解得,
∴直线AC的解析式为y=x+1;
(2)
解:∵BC⊥y轴,
∴B(0,3),
∵点P的横坐标为t,
∴P(t,t+1),
过点A作AM⊥BE交直线BC于M,过F作FN⊥BE交直线BC于N点,
∵AE⊥EF,
∴∠MEA+∠NEF=90°,∠MEA十∠MAE=90°,
∴∠NEF=∠MAE,
∵AE= EF,
∴△MAE≌△NEF (AAS),
∴ME=FN,MA=EN=3,
设E (m,3),F(m+3,2- m),
设直线CF的解析式为,
∴,解得,
∴y=-x+5,
∴G(5,0),
∴S=×6×(t+1)=t+3;
(3)
解:∵CG = GF, G(5,0),
∴F(8,-3),
∴E(5,3),
设直线EF的解析式为y=,
∴,解得
∴y=-2x+13,
联立方程组,
解得,
∴P(4,5),
∴H(4,0),
过点F作ST⊥x轴,过点P 作PS⊥ST交于S,过点K作KT⊥ST交于T,
∵FK⊥EF,
∴∠KFT+∠PFS=90°,∠KFT+∠FKT= 90°,
∴∠PFS =∠FKT,
∴△PFS∽△FKT,
∴,
设K(4,n),
∵KT=4,FT=-3-n,PS=4,FS=8,
∴,
∴n=-5,
∴K(4,-5).
8.(1)
如图,延长CE交AB于H,
∵∠ABC=45°,AD⊥BC,
∴∠ADC=∠ADB=90°,∠ABC=∠DAB=45°,
∵DE=CD,
∴∠DCE=∠DEC=∠AEH=45°,
∴∠BHC=∠BAD+∠AEH=90°,
∴CE⊥AB;
(2)
在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是一致的,理由如下:
如图2,延长交于H,
由旋转可得:CD=,=AD,
∵∠ADC=∠ADB=90°,
∴,
∵,
∴,
,
∵+∠DGC=90°,∠DGC=∠AGH,
∴∠DA+∠AGH=90°,
∴∠AHC=90°,
;
(3)
如图3,过点D作DH于点H,
∵△BED绕点D顺时针旋转30°,
∴,
,
,
∴AD=2DH,AH=DH=,
,
由(2)可知:,
,
∵AD⊥BC,CD=,
∴DG=1,CG=2DG=2,
∴CG=FG=2,
,
∴AG=2GF=4,
∴AD=AG+DG=4+1=5,
∴.
9.(1)
证法一:由折叠得,,,
∵
∴
∴
∴
∴四边形是平行四边形
∵
∴四边形是菱形.
证法二:
证明:由折叠得,,,
∵
∴
∴
∴
∴
∴四边形是菱形.
(2)
解: .
连接
由折叠可得,,
∵四边形是平行四边形
∴
又∵
∴
∵点P是的中点
∴
∴
∴
∴
∴
∴(SSS)
∴
又∵,即
∴
∴.
(3)
解:延长BA、CP相交于点F,
由题意,△AFP∽△DCP
∴ 即
∴
∵∠DCP=∠ECP,∠DCP=∠F
∴∠F=∠ECP
∴EF=EC=DC=10
∴.
故答案为.
10.(1)
证明: ,
,
,
,
绕点逆时针旋转.设旋转角为,
,
,
,
(2)
点恰好落在边中点处,,
,
,
,
垂直平分,
,
,
,
,,
,,
,
,
设,
则,
为的中点,
,
,
,
,
,
,
,
(3)
,,
,
是等腰直角三角形,
,
,
,
设,则,
,
,,
,
中,,
,
,
,
,
,
,
,
.
11.(1)
解:如图1中,连接.
,,
是等边三角形,
,,
,,
,,,
,
;
(2)
证明:如图2中,连接,延长到,使得,在上取一点,使得,连接.
,,
,
,
是等边三角形,
,
,
,,
,
,
,,
四边形是平行四边形,
,
四边形是菱形,
,
,
,,
,
,
;
(3)
解:如图3中,在上取一点,使得,连接.,过点作于点.
,
,,
,
点在上运动,设交圆弧于点,连接.
,,,
,
,
,
,
,
,
,
,
当点与重合时,的值最小,
,
,
,
,
,
,
,,
.
12.证明:(1)将沿翻折到处,四边形是正方形,
,,
,
,,
;
(2)解:延长,交于,如图:
设,
在中,,
,
解得,
,
,,
,
,即,
,,
,,
,,
,即,
,
设,则,
,
,
,即,
解得,
的长为;
(3)(Ⅰ)当时,延长交于,过作于,如图:
设,,则,
,
,
,
,
沿翻折得到,
,,,
是的角平分线,
,即①,
,
,,,
在中,,
②,
联立①②可解得,
;
(Ⅱ)当时,延长交延长线于,过作交延长线于,如图:
同理,
,即,
由得:,
可解得,
,
综上所述,的长为或.
13.(1)
解:∵四边形PQMN是正方形,
∴PN=MN,
∵,,,
∴,
解得:,
故答案为:;
(2)
解:能画出这样的正方形,理由为:
∵于点M,交AB于点P,于点Q,
∴∠NMQ=∠PNM=∠PQM=90°,
∴四边形PQMN是矩形,
∵四边形是正方形,
∴
∴△BN′M′∽△BNM,△BN′P′∽△BNP,
∴,,
∴,
∵P′N′= M′N′,
∴PN=MN,
∴四边形PQMN为正方形;
(3)
解:连接ME,
∵点E为BN的中点,∠NMB=90°,
∴ME=BE=NE,
∴∠EBM=∠EMQ,
∵,
∴∠EBM=∠PNE,
∴∠PNE=∠EMQ,
在△PNE和△EMQ中,
,
∴△PNE≌△EMQ(SAS),
∴EP=EQ;
(4)
解:∠QEM=75°,证明如下:
由(2)知,四边形PQMN是正方形,则∠NMB=90°,NM=MQ,
∵∠NMB=90°,∠NBM=30°,
∴∠MNB=90°-30°=60°,
∵NE=NM,
∴△EMN为等边三角形,
∴ME=NM,∠EMN=60°,
∴ME=MQ,∠EMQ=30°,
∴∠QEM=(180°-30°)=75°.
14.(1)
解:∵线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD.
解方程x2-7x+12=0得:x=4或3,
∴OA=4,OD=3,
∴点A的坐标为(-4,0),点D的坐标为(0,3);
故答案为:(-4,0),(0,3);
(2)
解:过D作AB的对称点D1,连接OD1,交AB于点P,此时△POD的周长最小,
∵△ABE是将△ABC沿AB折叠得到的,
∴点D1在AC上,
∵OA=4,OD=3,
∴AD=5,
∴AD1=5,
∴D1(-4,5),
设直线OD1的解析式为y=kx,
∴5=-4k,
∴k=-,
∴直线OD1的解析式为y=-x,
∵四边形AOBC是矩形,且△ABE是将△ABC沿AB折叠得到的,
∴AC∥OB,∠CAB=∠BAD,
∴∠CAB=∠BAD=∠ABD,
∴AD=BD=5,则OB=8,
∴B(0,8),
同理求得直线AB的解析式为y=2x+8,
解方程-x =2x+8,得x=-,
y=,
∴P(-,);
(3)
解:∵B(0,8),A (-4,0),
∴AB=4,
当BN为边时,
如图,若四边形BNMQ是正方形,则BN=MN,过点Q作QG⊥x轴于G,过点N作NI⊥x轴于I,
∵∠OAB=∠NAM,∠AOB=∠ANM=90°,
∴△AOB∽△ANM,
∴,即,
∴NM=,AM=,AN=,
∴OM=-4=,
∵AM×IN=AN×MN,
∴IN=,
∵四边形BNMQ是正方形,
∴QM=NM,∠QMN=90°,
∠QMG+∠NMI=90°,
又∵∠QMG+∠MQG=90°,
∴∠MQG=∠IMN,
又∵∠QGM=∠MIN=90°,
∴△QGM≌△MIN,
∴QG=IM=,MG=IN=,
OG=OM+MG=IN=,
点Q(,);
如图,若四边形BNQM是正方形,
同理,△AOB∽△ABM,
∴,即,
∴AM=20,
∴OM=20-4=,
∴M(16,0);
同理,点Q(8,-16);
如图,若四边形BMQN是正方形,
同理可求M(16,0);点Q(24,16);
当BN是对角线时,若四边形BMNQ是正方形,过点N作NF⊥x轴于F,
∵四边形BMNQ是正方形,
∴BM=NM,∠BMN=90°,
∠BMO+∠FMN=90°,
又∵∠BMO+∠OBM=90°,
∴∠FMN=∠OBM,
又∵∠NFM=∠MOB=90°,
∴△NFM≌△MOB(AAS),
∴BO=FM=8,OM=NF,
设点M(a,0),
∴OF=8-a,FN=a,
∴点N(a-8,-a),
∵点P在AB上,y=2x+8
∴-a=2(a-8)+8,
∴a=,
∴点M(,0);
过点Q作QH⊥y轴于H,
同理可证△QBH≌△BMO,
∴QH=BO=8,BH=OM=,
∴HO=,
∴点Q(-8,);
如图,若四边形BMNQ是正方形,
同理可求点M(-24,0),则点Q(8,-16),
综上所述:满足条件的点Q的个数为5个,点Q坐标为:(,)或(8,-16)或(24,16)或(-8,)或(8,-16).
15.(1)
①∵DE∥BC
∴△BAC∽△DAE
∵AB=AC,
∴AD=AE
∵由旋转可得:∠BAC=∠DAE,
∴∠CAE=∠BAD
∴△BAD≌△CAE
∴BD=CE,
②∠MAN=∠BAC
理由:如图1,∵DE∥BC
∴△BAC∽△DAE
∵AB=AC,
∴AD=AE
∵由旋转可得:∠BAC=∠DAE,
∴∠CAE=∠BAD
∴△BAD≌△CAE
∴BD=CE,∠ACE=∠ABD
∵DM=BD,EN=CE
∴BM=CN
△ABM≌△ACN
∴∠BAM=∠CAN
∴∠BAM-∠CAM=∠CAN-∠CAM
即∠MAN=∠BAC;
(2)
结论:∠MAN=∠BAC,AM=AN
∵△ABC∽△ADE,
∴
∴
∵∠CAE=∠DAE+∠CAD,∠BAD=∠BAC+∠CAD,
∴∠CAE=∠BAD,
∴△ADB∽△AEC,
∴
∵DM=BD,EN=CE
∵∠ADM=∠ABD+∠BAD,∠AEN=∠ACE+∠CAE,
∴∠ADM=∠AEN,
∴△ADM∽△AEN,
∴AM:AN=AD:AE=,
∴∠DAM=∠EAN,
∴∠NAE+∠MAE=∠NAE+∠MAE,
∴∠MAN=∠DAE,
∵∠DAE=∠BAC,
∴∠MAN=∠BAC.
AM=k AN,∠MAN=∠BAC.
16.(1)
解:①过作于,过作于,如图所示:
在矩形中,,
∵,点是的中点,
∴,
∵,,
∴,
在中,,,则,
∴,
∵,
∴,
在中,,,
则,
∵,,
∴,
∴,
故答案为:;
②点在上取不同位置,的值不变,.
过作于,过作于,如图所示:
在矩形中,,,
∵,
∴,
∵,
∴,
∵,
∴,
∴∠IGP=∠FEJ,
∴,
∴,
∴点在上取不同位置,的值不变,;
(2)
解:∵,
∴是直角三角形,
当是等腰直角三角形时,,
∵,
∴,
∵在(1)中有,
∴,
∴,
∴,
∴,
∵PA+PD=AD=BC=8,
∴,
∴;
(3)
以B为原点,BC为x轴,AB为y轴建立直角坐标系,连接GE,如图,
则有B点坐标为(0,0)、C点坐标为(8,0)、E点坐标为(8,3),
设P点坐标为(m,6)、G点坐标为(n,0),
∵P点坐标为(m,6)、E点坐标为(8,3),
∴设直线PE的解析式为,
则有:,解得:,
则直线PE的解析式为,
∴PE与y轴的交点F的坐标为,
∵E点坐标为(8,3),F的坐标为,
∴,
∵P点坐标为(m,6)、G点坐标为(n,0),
∴,
∵在(1)中已得,
∴,
∴,
∴
∵P点坐标为(m,6)、E点坐标为(8,3),
∴,
∵E点坐标为(8,3)、C点坐标为(8,0),
∴,
∵EF⊥PG,
∴在Rt△PGE中,,
又∵在Rt△GEC中,,
∴,
即:,
∵P点在射线DA上,
∴m<8,
则设8-m=t,即t>0,
∴,
∴,
∵,
∴,
∴,
则的最小值为,
即GC的最小值为:.
1.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,点C是线段上一点,把沿直线翻折,点O恰好落在上的点D处,为折痕.
(1)求线段的长;
(2)求直线的解析式;
(3)若M是射线上的一个动点,在坐标平面内是否存在点P,使以A,B,M,P为顶点的四边形是以为一边的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
2.在△ABC中,CA=CB,∠ACB=α.点P是平面内不与点A,C重合的任意一点,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当α=60°时,的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当α=90°时,请写出,并就图2的情形说明理由.
(3)解决问题
当α=90°时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时的值.
3.问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,∠B=∠A=∠EDF.
(1)初步尝试:如图①,当△ABC是等边三角形,判断:△ADM △BND(填相似或全等);
(2)类比探究:如图②,当AC=BC时,上述结论是否还成立?请说明理由.
(3)延伸拓展:如图③,在(2)的条件下,当点D在BA的延长线上运动到点M与点C重合时,若S△ADM:S△BND=1:2,BN:BM=1:3,AD=1,则DN= .
4.
(1)[基础巩固]如图①,在三角形纸片ABC中,,将折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为______;
(2)[思维提高]如图②,在三角形纸片ABC中,,,将折叠,使点B与点C重合,折痕为MN,求的值;
(3)[拓展延伸]如图③,在三角形纸片ABC中,,,,将沿过顶点C的直线折叠,使点B落在边AC上的点处,折痕为CM.求线段AC的长;
5.直线y=2x+4与x轴交于点A,与y轴交于点B,点C在x轴的正半轴上,△ABC面积为10.
(1)直接写出点C的坐标;
(2)如图1,F为线段AB的中点,点G在y轴上,以FG为边,向右作正方形FGQP,点Q落在直线BC上,求点G的坐标;
(3)如图2,M在射线BA上,点N在射线BC上,直线MN交y轴于H点,若HB=HM,求的值.
6.如图1,在矩形ABCD中,,,点E在AB边上,且.点F是BC边上的动点.将沿EF折叠得到.直线GF与直线AB的交点为H.
(1)如图2,点F与点C重合时,求与的面积比;
(2)如图3,当H在点A的上方,且满足三角形HEF是等腰三角形时,求线段EH的长.
(3)在点F的运动过程中,以E、G、H为顶点的三角形能否与以B、C、D为顶点的三角形相似?若能,求BF的长;若不存在,请说明理由.
7.已知:在平面直角坐标系xOy中,直线过点A(-1,0)、C(2,3)两点.
(1)如图1,求直线的解析式;
(2)如图2,过点C作轴于点B,点E是射线BC上一点,连接AE,过点E作,且.连接FC交x轴于点G,延长FE交直线AC于点P,连接PG,设点P的横坐标为t,△PAG的面积为S,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点P作轴于点H,过点F作交PH延长线于点K.若,求点K坐标.
8.如图1,在中,于点D,在DA上取点E,使,连接BE、CE.
(1)直接写出CE与AB的位置关系;
(2)如图2,将绕点D旋转,得到(点,分别与点B,E对应),连接,在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致 请说明理由;
(3)如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若,求的长.
9.综合与实践:
数学活动课上,老师让同学们根据下面情境提出问题并解答.
问题情境:在中,点P是边上一点.将沿直线折叠,点D的对应点为E.
“兴趣小组”提出的问题是:如图1,若点P与点A重合,过点E作,与交于点F,连接,则四边形是菱形.
(1)数学思考:请你证明“兴趣小组”提出的问题;
(2)拓展探究:“智慧小组”提出的问题是:如图2,当点P为的中点时,延长交于点F,连接.试判断与的位置关系,并说明理由.
请你帮助他们解决此问题.
(3)问题解决:“创新小组”在前两个小组的启发下,提出的问题是:如图3,当点E恰好落在边上时,,,.则的长为___________.(直接写出结果)
10.已知中,点、分别在边、上,且,将绕点逆时针旋转.设旋转角为
(1)试说明;
(2)若,,当时,若点恰好落在边中点处,求的值;
(3)若,,当点恰好落在边上时,延长交于,若,求的值.
11.如图1,在四边形ABCD中,,,.
(1)求∠ACD的度数;
(2)如图2,F为线段CD的中点,连接BF,求证:;
(3)如图3,若,线段BC上有一动点M,连接OM,将沿OM所在直线翻折至的位置,P为B的对应点,连接PA,PC,当的值最小时,设O到直线PC的距离为,PC的长度为,直接写出的值.
12.(1)【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
(2)【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(3)【拓展应用】如图③,在菱形中,为边上的三等分点,将沿翻折得到,直线交于点求的长.
13.小亮在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在中,于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,且.若,,则正方形PQMN的边长等于______.
(2)操作:能画出这类正方形吗?小亮按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画,在AB上任取一点,画正方形,使,在BC边上,在内,连结并延长交AC于点N,画于点M,交AB于点P,于点Q,得到四边形PQMN.
(3)推理:如图3,若点E是BN的中点,求证:.
(4)拓展:在(2)的条件下,射线BN上截取,连结EQ,EM(如图4).当时,猜想的度数,并尝试证明.
请帮助小亮解决“温故”、“推理”、“拓展”中的问题.
14.矩形AOBC在平面直角坐标系中的位置如图所示,点A在x轴的负半轴上,点B在y轴的正半轴上,连接AB,将△ABC沿AB折叠得△ABE,AE交y轴于点D,线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD.
(1)请直接写出点A的坐标为________,点D的坐标为________;
(2)点P为直线AB上一点,连接PO、PD,当△POD的周长最小时,求点P的坐标;
(3)点M在x轴上,点N在直线AB上,坐标平面内是否在点Q,使以B、M、N、Q为顶点的四边形为正方形 若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
15.问题情境:如图1所示,在△ABC中,D、E分别是AB、AC上的点,DEBC,在图1中将ADE绕A点顺时针旋转一定角度,得到图2,然后将BD、CE分别延长至M、N,使DM=BD,EN=CE,得到图3,请解答下列问题:
(1)猜想证明:若AB=AC,请探究下列数量关系:
①在图2中,BD与CE的数量关系是_________.
②在图3中,猜想∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)拓展应用:其他条件不变,若AB=AC,按上述操作方法,得到图4,请你继续探究:∠MAN与∠BAC的数量关系?AM与AN的数量关系?直接写出你的猜想.
16.如图,矩形中,,,点是的中点,是射线上一点,延长交直线于,过作,分别交射线、直线于、.
(1)①当时,______;
②点在上取不同位置,的值是否变化?若不变,求出它的值,若改变,请说明理由;
(2)连接,当是等腰直角三角形时,求的长;
(3)直接写出的最小值______.
答案
1.(1)
解:令x=0,则y=6,
∴B(0,6),
令y=0,则x=8,
∴A(8,0),
∴AB=10;
(2)
解:由折叠的性质可知,OC=CD,OB=CD,
∵OB=6,
∴BD=6,
∵AB=10,
∴AD=4,
在Rt△ACD中,AC2=CD2+AD2,
∴(8OC)2=CO2+42,
∴CO=3,
∴C(3,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴y=2x+6;
(3)
解:存在点P,使以A,B,M,P为顶点的四边形是以AB为一边的矩形,理由如下:
设M(t,-2t+6),(t>0),P(x,y),
当以AB为矩形的一边时,BM为矩形的对角线,
∴,
过点M作EF∥x轴,过点A作AF⊥EF交于F,过点P作PE⊥EF交于点E,
∵∠AMP=90°,
∴∠PME+∠AMF=90°,
∵∠AMF+∠MAF=90°,
∴∠AMF=∠PME,
∴△AMF∽△MPE,
∴,
∵AF=2t-6,MF=8-t,PE=y+2t-6,EM=t-x,
∴,
∴,
解得t=5,
∴x=3,y=2,
∴P(3,2).
2.
(1)解:如图1中,延长CP交BD的延长线于E.∵CA=CB,∠ACB=60°,∴ CAB为等边三角形,又∵将线段AP绕点P逆时针旋转60°得到线段DP∴AP=DP,∠APD=60°∴ APD为等边三角形,∴CA=BA,PA=DA,∴∠PAD=∠CAB=60°,∴∠PAD-∠PAB=∠CAB-∠PAB∴∠CAP=∠BAD,∵CA=BA,PA=DA,∴△CAP≌△BAD(SAS),∴PC=BD,∠ACP=∠ABD,∵∠AOC=∠BOE,∴∠BEO=∠CAO=60°,∴=1,故答案为1,60°.
(2)=,理由:如图2中,设BD交AC于点O.
∵∠PAD=∠CAB=45°,∴∠PAC=∠DAB,∵==,∴△DAB∽△PAC,∴∠PCA=∠DBA, ==,
如图3﹣1中,当点D在线段PC上时.
∵CE=EA,CF=FB,∴EF∥AB,∴∠EFC=∠ABC=45°,∵∠PAO=45°,∴∠PAO=∠OFH,∵∠POA=∠FOH,∴∠H=∠APO,∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA,∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°,∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,PD=a,∴=.
解法二:在Rt△PAD中,∵E是AC的中点,∴PE=EA=EC,∴∠EPC=∠ECP,∵∠CEF=45°=∠EPC+∠ECP,∴∠EPC=∠ECP=22.5°,∵∠PDA=45°=∠ACD+∠DAC,∴∠DAC=22.5°,∴AD=DC,设PD=a,则AD=DC=a,∴,如图3﹣3中,当点P在线段CD上时,同理可得DA=DC,
设AD=a,PD=a,∴PC=a﹣a,∴.
3.
(1)解:如图①,∵△ABC是等边三角形,∠B=∠A=∠EDF,∴∠B=∠A=∠EDF=60°,∴∠AMD=180°﹣60°﹣∠ADM=120°﹣∠ADM,∠BDN=180°﹣60°﹣∠ADM=120°﹣∠ADM,∴∠AMD=∠BDN,∴△ADM∽△BND,故答案为:相似.
(2)解:成立,如图②,∵AC=BC,∴∠B=∠A,∴∠B=∠A=∠EDF,设∠B=∠A=∠EDF=x,∵∠AMD=180°﹣∠A﹣∠ADM=180°﹣x﹣∠ADM,∠BDN=180°﹣∠EDF﹣∠ADM=180°﹣x﹣∠ADM,∴∠AMD=∠BDN,∴△ADM∽△BND.
(3)解:如图③,作CG⊥AB于点G,设S△CDN=m,则∠CGD=∠CGB=90°,设∠CBA=∠CAB=∠EDF=x,∵∠DCA=∠CAB﹣∠CDB=x﹣∠CDB,∠NDB=∠EDF﹣∠CDB=x﹣∠CDB,∴∠DCA=∠NDB;∵∠CAD=180°﹣∠CAB=180°﹣x,∠DBN=180°﹣∠CBA=180°﹣x,∴∠CAD=∠DBN,∴△ADC∽△BND,∴;∵点M与点C重合,S△ADM:S△BND=1:2,BN:BM=1:3,∴S△ADC:S△BND=1:2,BN:BC=1:3,∴S△BND=S△CDN=,∴S△ADC=S△BND=,∴S△ABC=m﹣﹣m=m,∴,∵AD=1,∴AB=5AD=5,∵AC=BC,∴AG=BG=AB=,∴DG=;∵,∴,∴DN=CD,BN=AD=,∴BC=3BN=,∴CG2=BC2﹣BG2=,∴CD=,∴DN=,故答案为: .
4.
(1)解:如图①中,∵△ABC折叠,使点B与点C重合,折痕为MN,∴MN垂直平分线段BC,∴CN=BN,∵∠MNB=∠ACB=90°,∴MN∥AC,∵CN=BN,∴AM=BM.故答案为AM=BM.
(2)如图②中,∵CA=CB=6,∴∠A=∠B,由题意MN垂直平分线段BC,∴BM=CM,∴∠B=∠MCB,∴∠BCM=∠A,∵∠B=∠B,∴△BCM∽△BAC,∴,∴,∴,∴,∴.
(3)如图③中,由折叠的性质可知,
CB=CB′=6,∠BCM=∠ACM,∵∠ACB=2∠A,∴∠BCM=∠A,∵∠B=∠B,∴△BCM∽△BAC,∴∴,∴BM=4,∴AM=CM=5,∴,∴.
5.(1)
解:∵直线y=2x+4与x轴交于点A,与y轴交于点B,
令y=0,y=﹣2,令x=0,x=4,
∴A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∵,
∴AC=5,
∴OC=3,
∴C(3,0),
(2)
解:设直线BC的解析式为:y=kx+b,把B(0,4),C(3,0),代入得:
,解得: ,
∴直线BC的解析式为:;
由(1)知:A(﹣2,0),B(0,4),
∵F为线段AB的中点,
∴F(-1,2),
设G(0,n),
①当n>2时,如图,
点Q落在BC上时,过G作直线MN平行于x轴,过点F,Q作该直线MN的垂线,垂足分别为M,N,
∵四边形FGQP是正方形,
∴∠FGQ=90°,FG=QG,
∴∠FGM=90°﹣∠NGQ=∠GQN,
而∠FMG=∠GNQ=90°,
∴△FMG≌△GNQ(AAS),
∴MG=NQ=1,FM=GN=n﹣2,
∴Q(n﹣2,n﹣1),
∴Q在直线上,
∴n﹣1=+4,
∴n=,
∴G(0,);
①当n<2时,如图,
点Q落在BC上时,过G作直线MN平行于x轴,过点F,Q作该直线MN的垂线,垂足分别为M,N.
∵四边形FGQP是正方形,
∴∠FGQ=90°,FG=QG,
∴∠FGM=90°﹣∠NGQ=∠GQN,
∵∠FMG=∠GNQ=90°,
∴△FMG≌△GNQ(AAS),
∴MG=NQ=1,FM=GN=2﹣n,
∴Q(2﹣n,n+1),
∴Q在直线上,
∴n+1=+4,
∴n=﹣1,
∴G(0,﹣1);
综上所述,满足条件的点G坐标为(0,)或(0,﹣1);
(3)
解:过点M作MP∥x轴交BC于点P,交y轴于Q,
∵B(0,4),C(3,0),A(﹣2,0),
∴AC=5,OB=4,OC=3,
在Rt△BOC中,
由勾股定理得:BC=,
∴AC=BC=5,
∴∠ABC=∠BAC,
∵MP∥x轴,
∴∠BMP=∠BAC,∠AOB=∠MQH=90°,
∴∠BMP=∠ABC,
∵HM=HB,
∴∠HBM=∠HMB,
∴∠ABC﹣∠HBM=∠BMP﹣∠HMB,
即∠HBN=∠HMQ,
∴∠MHQ≌△BHN(ASA),
∴∠MNB=∠MQH=∠BOC=90°,
∵∠OBC=∠OBC,
∴△BHN∽△BCO,
∴,
∴.
6.(1)如图,∵∠GHE=∠BHC,∠EGH=∠CBH,∴△HEG∽△HCB,根据面积之比等于相似比的平方,∴,∵EG=BE=AB-AE=2,∴..
(2)根据题意,EF=EH,根据折叠性质,等腰三角形三线合一性质,得FB=FG=GH,∴∠BHF=30°,∵EG=BE=AB-AE=2,∴EH=4.
(3)∵ BC=5,DC=3,四边形ABCD是矩形,∴BD==.根据题意,得到CH⊥BD时,△HEG∽△BCD,∴ ,∴ ,解得
.∵△HEG∽△HFB,∴△HFB∽△BDC,∴ ,∴ ,解得.当H在下方时,∵ BC=5,DC=3,四边形ABCD是矩形,∴BD==.根据题意,得到CH⊥BD时,△HEG∽△BCD,∴ ,∴ ,解得,∴.∵△HEG∽△HFB,∴△HFB∽△BDC,∴ ,∴ ,解得.
7.(1)
设直线AC的解析式为y=kx+b,
,解得,
∴直线AC的解析式为y=x+1;
(2)
解:∵BC⊥y轴,
∴B(0,3),
∵点P的横坐标为t,
∴P(t,t+1),
过点A作AM⊥BE交直线BC于M,过F作FN⊥BE交直线BC于N点,
∵AE⊥EF,
∴∠MEA+∠NEF=90°,∠MEA十∠MAE=90°,
∴∠NEF=∠MAE,
∵AE= EF,
∴△MAE≌△NEF (AAS),
∴ME=FN,MA=EN=3,
设E (m,3),F(m+3,2- m),
设直线CF的解析式为,
∴,解得,
∴y=-x+5,
∴G(5,0),
∴S=×6×(t+1)=t+3;
(3)
解:∵CG = GF, G(5,0),
∴F(8,-3),
∴E(5,3),
设直线EF的解析式为y=,
∴,解得
∴y=-2x+13,
联立方程组,
解得,
∴P(4,5),
∴H(4,0),
过点F作ST⊥x轴,过点P 作PS⊥ST交于S,过点K作KT⊥ST交于T,
∵FK⊥EF,
∴∠KFT+∠PFS=90°,∠KFT+∠FKT= 90°,
∴∠PFS =∠FKT,
∴△PFS∽△FKT,
∴,
设K(4,n),
∵KT=4,FT=-3-n,PS=4,FS=8,
∴,
∴n=-5,
∴K(4,-5).
8.(1)
如图,延长CE交AB于H,
∵∠ABC=45°,AD⊥BC,
∴∠ADC=∠ADB=90°,∠ABC=∠DAB=45°,
∵DE=CD,
∴∠DCE=∠DEC=∠AEH=45°,
∴∠BHC=∠BAD+∠AEH=90°,
∴CE⊥AB;
(2)
在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是一致的,理由如下:
如图2,延长交于H,
由旋转可得:CD=,=AD,
∵∠ADC=∠ADB=90°,
∴,
∵,
∴,
,
∵+∠DGC=90°,∠DGC=∠AGH,
∴∠DA+∠AGH=90°,
∴∠AHC=90°,
;
(3)
如图3,过点D作DH于点H,
∵△BED绕点D顺时针旋转30°,
∴,
,
,
∴AD=2DH,AH=DH=,
,
由(2)可知:,
,
∵AD⊥BC,CD=,
∴DG=1,CG=2DG=2,
∴CG=FG=2,
,
∴AG=2GF=4,
∴AD=AG+DG=4+1=5,
∴.
9.(1)
证法一:由折叠得,,,
∵
∴
∴
∴
∴四边形是平行四边形
∵
∴四边形是菱形.
证法二:
证明:由折叠得,,,
∵
∴
∴
∴
∴
∴四边形是菱形.
(2)
解: .
连接
由折叠可得,,
∵四边形是平行四边形
∴
又∵
∴
∵点P是的中点
∴
∴
∴
∴
∴
∴(SSS)
∴
又∵,即
∴
∴.
(3)
解:延长BA、CP相交于点F,
由题意,△AFP∽△DCP
∴ 即
∴
∵∠DCP=∠ECP,∠DCP=∠F
∴∠F=∠ECP
∴EF=EC=DC=10
∴.
故答案为.
10.(1)
证明: ,
,
,
,
绕点逆时针旋转.设旋转角为,
,
,
,
(2)
点恰好落在边中点处,,
,
,
,
垂直平分,
,
,
,
,,
,,
,
,
设,
则,
为的中点,
,
,
,
,
,
,
,
(3)
,,
,
是等腰直角三角形,
,
,
,
设,则,
,
,,
,
中,,
,
,
,
,
,
,
,
.
11.(1)
解:如图1中,连接.
,,
是等边三角形,
,,
,,
,,,
,
;
(2)
证明:如图2中,连接,延长到,使得,在上取一点,使得,连接.
,,
,
,
是等边三角形,
,
,
,,
,
,
,,
四边形是平行四边形,
,
四边形是菱形,
,
,
,,
,
,
;
(3)
解:如图3中,在上取一点,使得,连接.,过点作于点.
,
,,
,
点在上运动,设交圆弧于点,连接.
,,,
,
,
,
,
,
,
,
,
当点与重合时,的值最小,
,
,
,
,
,
,
,,
.
12.证明:(1)将沿翻折到处,四边形是正方形,
,,
,
,,
;
(2)解:延长,交于,如图:
设,
在中,,
,
解得,
,
,,
,
,即,
,,
,,
,,
,即,
,
设,则,
,
,
,即,
解得,
的长为;
(3)(Ⅰ)当时,延长交于,过作于,如图:
设,,则,
,
,
,
,
沿翻折得到,
,,,
是的角平分线,
,即①,
,
,,,
在中,,
②,
联立①②可解得,
;
(Ⅱ)当时,延长交延长线于,过作交延长线于,如图:
同理,
,即,
由得:,
可解得,
,
综上所述,的长为或.
13.(1)
解:∵四边形PQMN是正方形,
∴PN=MN,
∵,,,
∴,
解得:,
故答案为:;
(2)
解:能画出这样的正方形,理由为:
∵于点M,交AB于点P,于点Q,
∴∠NMQ=∠PNM=∠PQM=90°,
∴四边形PQMN是矩形,
∵四边形是正方形,
∴
∴△BN′M′∽△BNM,△BN′P′∽△BNP,
∴,,
∴,
∵P′N′= M′N′,
∴PN=MN,
∴四边形PQMN为正方形;
(3)
解:连接ME,
∵点E为BN的中点,∠NMB=90°,
∴ME=BE=NE,
∴∠EBM=∠EMQ,
∵,
∴∠EBM=∠PNE,
∴∠PNE=∠EMQ,
在△PNE和△EMQ中,
,
∴△PNE≌△EMQ(SAS),
∴EP=EQ;
(4)
解:∠QEM=75°,证明如下:
由(2)知,四边形PQMN是正方形,则∠NMB=90°,NM=MQ,
∵∠NMB=90°,∠NBM=30°,
∴∠MNB=90°-30°=60°,
∵NE=NM,
∴△EMN为等边三角形,
∴ME=NM,∠EMN=60°,
∴ME=MQ,∠EMQ=30°,
∴∠QEM=(180°-30°)=75°.
14.(1)
解:∵线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD.
解方程x2-7x+12=0得:x=4或3,
∴OA=4,OD=3,
∴点A的坐标为(-4,0),点D的坐标为(0,3);
故答案为:(-4,0),(0,3);
(2)
解:过D作AB的对称点D1,连接OD1,交AB于点P,此时△POD的周长最小,
∵△ABE是将△ABC沿AB折叠得到的,
∴点D1在AC上,
∵OA=4,OD=3,
∴AD=5,
∴AD1=5,
∴D1(-4,5),
设直线OD1的解析式为y=kx,
∴5=-4k,
∴k=-,
∴直线OD1的解析式为y=-x,
∵四边形AOBC是矩形,且△ABE是将△ABC沿AB折叠得到的,
∴AC∥OB,∠CAB=∠BAD,
∴∠CAB=∠BAD=∠ABD,
∴AD=BD=5,则OB=8,
∴B(0,8),
同理求得直线AB的解析式为y=2x+8,
解方程-x =2x+8,得x=-,
y=,
∴P(-,);
(3)
解:∵B(0,8),A (-4,0),
∴AB=4,
当BN为边时,
如图,若四边形BNMQ是正方形,则BN=MN,过点Q作QG⊥x轴于G,过点N作NI⊥x轴于I,
∵∠OAB=∠NAM,∠AOB=∠ANM=90°,
∴△AOB∽△ANM,
∴,即,
∴NM=,AM=,AN=,
∴OM=-4=,
∵AM×IN=AN×MN,
∴IN=,
∵四边形BNMQ是正方形,
∴QM=NM,∠QMN=90°,
∠QMG+∠NMI=90°,
又∵∠QMG+∠MQG=90°,
∴∠MQG=∠IMN,
又∵∠QGM=∠MIN=90°,
∴△QGM≌△MIN,
∴QG=IM=,MG=IN=,
OG=OM+MG=IN=,
点Q(,);
如图,若四边形BNQM是正方形,
同理,△AOB∽△ABM,
∴,即,
∴AM=20,
∴OM=20-4=,
∴M(16,0);
同理,点Q(8,-16);
如图,若四边形BMQN是正方形,
同理可求M(16,0);点Q(24,16);
当BN是对角线时,若四边形BMNQ是正方形,过点N作NF⊥x轴于F,
∵四边形BMNQ是正方形,
∴BM=NM,∠BMN=90°,
∠BMO+∠FMN=90°,
又∵∠BMO+∠OBM=90°,
∴∠FMN=∠OBM,
又∵∠NFM=∠MOB=90°,
∴△NFM≌△MOB(AAS),
∴BO=FM=8,OM=NF,
设点M(a,0),
∴OF=8-a,FN=a,
∴点N(a-8,-a),
∵点P在AB上,y=2x+8
∴-a=2(a-8)+8,
∴a=,
∴点M(,0);
过点Q作QH⊥y轴于H,
同理可证△QBH≌△BMO,
∴QH=BO=8,BH=OM=,
∴HO=,
∴点Q(-8,);
如图,若四边形BMNQ是正方形,
同理可求点M(-24,0),则点Q(8,-16),
综上所述:满足条件的点Q的个数为5个,点Q坐标为:(,)或(8,-16)或(24,16)或(-8,)或(8,-16).
15.(1)
①∵DE∥BC
∴△BAC∽△DAE
∵AB=AC,
∴AD=AE
∵由旋转可得:∠BAC=∠DAE,
∴∠CAE=∠BAD
∴△BAD≌△CAE
∴BD=CE,
②∠MAN=∠BAC
理由:如图1,∵DE∥BC
∴△BAC∽△DAE
∵AB=AC,
∴AD=AE
∵由旋转可得:∠BAC=∠DAE,
∴∠CAE=∠BAD
∴△BAD≌△CAE
∴BD=CE,∠ACE=∠ABD
∵DM=BD,EN=CE
∴BM=CN
△ABM≌△ACN
∴∠BAM=∠CAN
∴∠BAM-∠CAM=∠CAN-∠CAM
即∠MAN=∠BAC;
(2)
结论:∠MAN=∠BAC,AM=AN
∵△ABC∽△ADE,
∴
∴
∵∠CAE=∠DAE+∠CAD,∠BAD=∠BAC+∠CAD,
∴∠CAE=∠BAD,
∴△ADB∽△AEC,
∴
∵DM=BD,EN=CE
∵∠ADM=∠ABD+∠BAD,∠AEN=∠ACE+∠CAE,
∴∠ADM=∠AEN,
∴△ADM∽△AEN,
∴AM:AN=AD:AE=,
∴∠DAM=∠EAN,
∴∠NAE+∠MAE=∠NAE+∠MAE,
∴∠MAN=∠DAE,
∵∠DAE=∠BAC,
∴∠MAN=∠BAC.
AM=k AN,∠MAN=∠BAC.
16.(1)
解:①过作于,过作于,如图所示:
在矩形中,,
∵,点是的中点,
∴,
∵,,
∴,
在中,,,则,
∴,
∵,
∴,
在中,,,
则,
∵,,
∴,
∴,
故答案为:;
②点在上取不同位置,的值不变,.
过作于,过作于,如图所示:
在矩形中,,,
∵,
∴,
∵,
∴,
∵,
∴,
∴∠IGP=∠FEJ,
∴,
∴,
∴点在上取不同位置,的值不变,;
(2)
解:∵,
∴是直角三角形,
当是等腰直角三角形时,,
∵,
∴,
∵在(1)中有,
∴,
∴,
∴,
∴,
∵PA+PD=AD=BC=8,
∴,
∴;
(3)
以B为原点,BC为x轴,AB为y轴建立直角坐标系,连接GE,如图,
则有B点坐标为(0,0)、C点坐标为(8,0)、E点坐标为(8,3),
设P点坐标为(m,6)、G点坐标为(n,0),
∵P点坐标为(m,6)、E点坐标为(8,3),
∴设直线PE的解析式为,
则有:,解得:,
则直线PE的解析式为,
∴PE与y轴的交点F的坐标为,
∵E点坐标为(8,3),F的坐标为,
∴,
∵P点坐标为(m,6)、G点坐标为(n,0),
∴,
∵在(1)中已得,
∴,
∴,
∴
∵P点坐标为(m,6)、E点坐标为(8,3),
∴,
∵E点坐标为(8,3)、C点坐标为(8,0),
∴,
∵EF⊥PG,
∴在Rt△PGE中,,
又∵在Rt△GEC中,,
∴,
即:,
∵P点在射线DA上,
∴m<8,
则设8-m=t,即t>0,
∴,
∴,
∵,
∴,
∴,
则的最小值为,
即GC的最小值为:.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
