九年级数学上册试题 4.2 平行线分线段成比例 -北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.2 平行线分线段成比例 -北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 22:23:59 | ||
图片预览

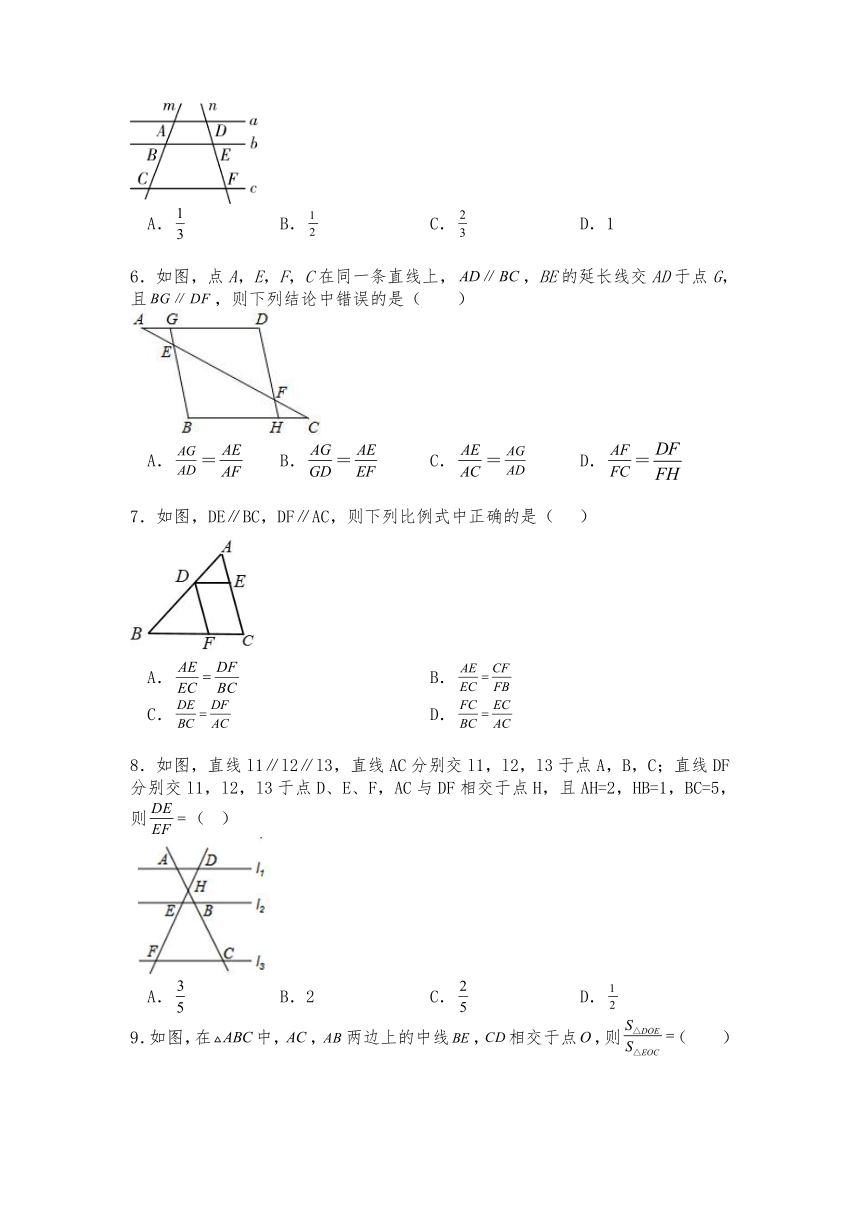

文档简介
4.2 平行线分线段成比例
第一课时
一、单选题
1.如图,在△ABC中,DEBC,若,则等于( )
A. B. C. D.
2.如图,AB∥CD,AD与BC交于点O,则下列比例式中正确的是( )
A. B. C. D.
3.中,直线交于,交于点,那么能推出的条件是( )
A. B. C. D.
4.如图,已知:AB、CD相交于点O,由下列哪一组条件可以推出AC∥BD( )
A., B.
C. D.
5.如图,已知直线a//b//c,直线m分别交直线a,b,c于点A,B,C;直线n分别交直线a,b,c于点D,E,F.若,则=( )
A. B. C. D.1
6.如图,点A,E,F,C在同一条直线上,,BE的延长线交AD于点G,且,则下列结论中错误的是( )
A.= B.= C.= D.=
7.如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
A. B.
C. D.
8.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则( )
A. B.2 C. D.
9.如图,在中,,两边上的中线,相交于点,则( )
A. B. C. D.
10.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,已知,、交于点,若,则______.
12.如图,已知,则______,______,______,______.
13.如图,,如果,那么________.
14.如图,在中,是中线,是重心,过点作,分别交、于点、,若,则____________.
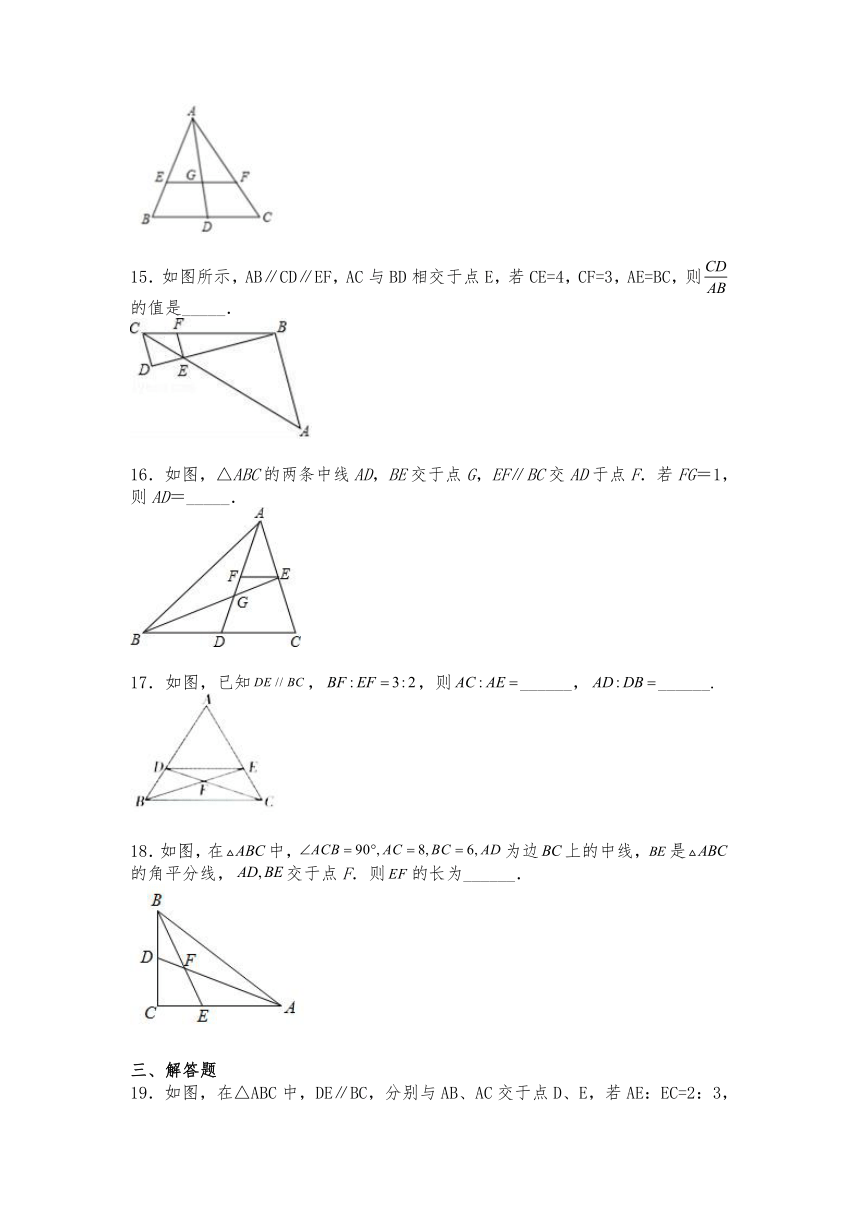
15.如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则 的值是_____.
16.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=1,则AD=_____.
17.如图,已知,,则______,______.
18.如图,在中,为边上的中线,是的角平分线,交于点F.则的长为______.
三、解答题
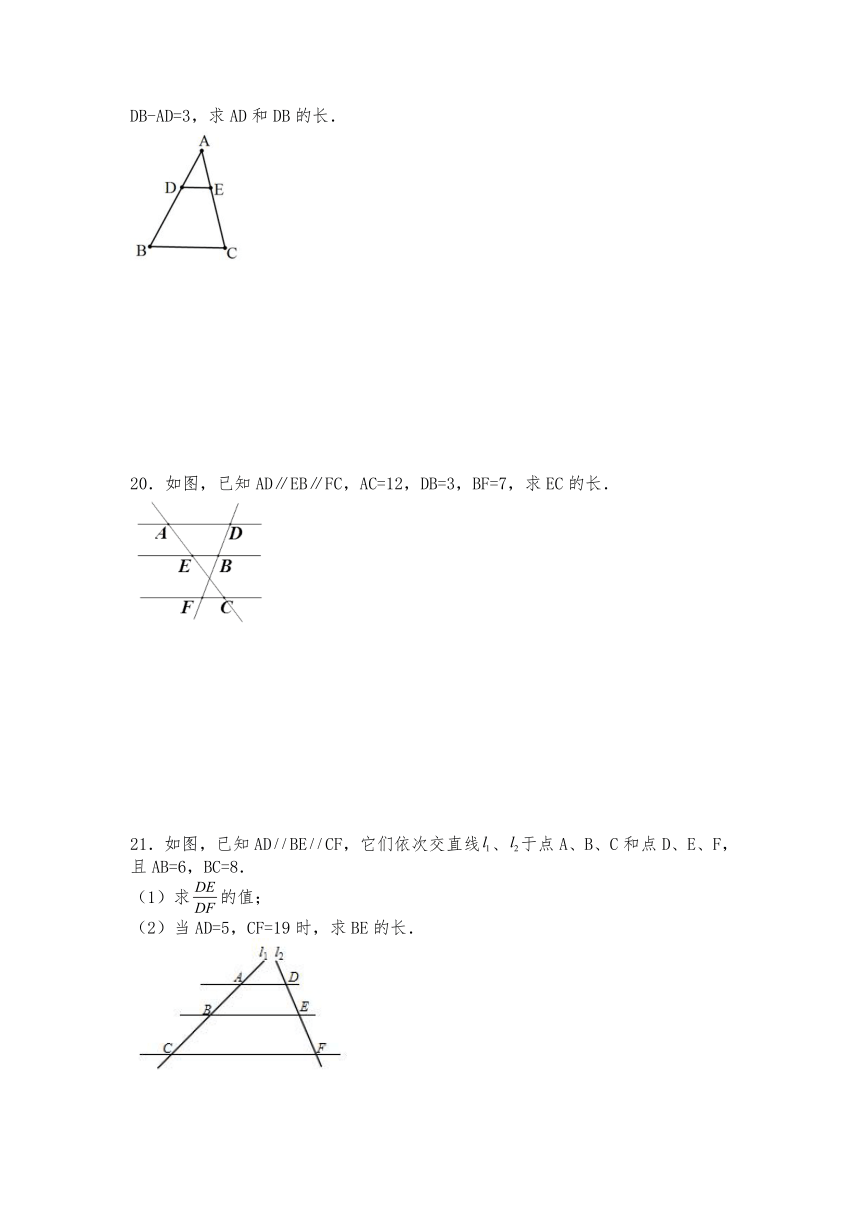
19.如图,在△ABC中,DE∥BC,分别与AB、AC交于点D、E,若AE:EC=2:3,DB-AD=3,求AD和DB的长.
20.如图,已知AD∥EB∥FC,AC=12,DB=3,BF=7,求EC的长.
21.如图,已知ADBECF,它们依次交直线、于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
22.如图,在△ABC中,DE∥BC,分别与AB、AC交于点D、E,点F在BC上,DE交AF于点G,AD=2BD,AE=5,求:(1);(2)AC的长.
23.如图,在△ABC中,点D、F是在边AB 上,点E在边AC上,且FE∥CD,线段AD是线段AF与AB的比例中项.
求证:DE∥BC
24.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
第二课时
一、单选题
1.如图,在△ABC中,点D在边BC上,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.; B.; C.; D..
2.如图,在中,D是上一点,连接是的中点,连接并延长交于点E,则的值为( )
A. B. C. D.
3.在中,D.F.E分别在边BC.AB.AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
A. B. C. D.
4.如图,在中,,,已知,则的长是
A. B.3 C. D.4
5.如图,,与相交于点,过点的直线交于点,交于点.若,,,则的长为( )
A. B. C. D.4
6.如图,在中,点,点为边的三等分点,与交于点,则下列比例式正确的是( )
A. B. C. D.
7.如图,在△ABC中,M是AC的中点,P,Q为BC边上的点,且BP=PQ=CQ,BM与AP,AQ分别交于D,E点,则BD∶DE∶EM等于
A.3∶2∶1 B.4∶2∶1 C.5∶3∶2 D.5∶2∶1
8.在中,、是边上的三等分点,是边上的中线,、分为三段的长分别是、、,若这三段有,则等于( )
A. B. C. D.
二、填空题
9.如图,的中线、交于点,点在边上,,那么的值是__________.
10.如图,直线,且每相邻两条直线的距离相等.若直线分别与相交于点,则为___________.
11.如图,在中,为上一点,且,过点作交于点,连接,过点作交于点.若,则______.
12.如图,在中,点是边的中点,直线交边于点,交的延长线于点,如果,那么的值为____.(用含、的式子表示)
13.如图中,、为的三等份点,为的中点,与、分别交于、,则________.
14.如图,在中,,.在边上有个不同的点,,,¨¨¨¨,,过这个点分别作的内接矩形,,¨¨¨¨,,设每个矩形的周长分别为,,¨¨¨¨,,则¨¨¨¨________.
三、解答题
15.如图,中,是中线,点在上,且,的延长线交于,求的值.
16.如图,MN经过ABC的顶点A,MN∥BC,AM=AN,MC交AB于D,NB交AC于E.
(1)求证:DE∥BC;
(2)联结DE,如果DE=1,BC=3,求MN的长.
17.如图,在中,,,点为边上的中点,连接,过点作于点,延长交于点,求的值.
18.如图,点D、E分别在△ABC的边AB、AC上,DEBC.
(1)若S△ADE=2,S△BCE=7.5,求S△BDE;
(2)若S△BDE=m,S△BCE=n,求S△ABC(用m、n表示).
19.已知:如图,在△ABC中,AD是边BC上的中线,点E在线段DC上,EF∥AB交边AC于点F,EG∥AC交边AB于点G,FE的延长线与AD的延长线交于点H.
求证:GF = BH.
20.如图(1),,直线AB和CH交于点O,分别交于D、E两点,已知,,.
(1)尝试探究:在图(1)中,求DB和AD的长;
(2)类比延伸:平移AB使得A与H重合,如图(2)所示,过点D作,若,求线段BF的长;
(3)拓展迁移:如图(3),若的面积是10,点D、E分别位于AB、CA上,,点F在BC上且,,如果的面积和四边形FCED的面积相等,求这个相等的面积.
21.如图1.在△ABC中,矩形EFGH的一边EF在AB上,顶点G、H分别在BC、AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD.矩形DFGI恰好为正方形.
(1)求正方形DFGI的边长;
(2)如图2,延长AB至P.使得AC=CP,将矩形EFGH沿BP的方向向右平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?
(3)如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG、DB相交于点M、N,求△MNG′的周长.
第一课时答案
一、单选题
C.D.C.C.A.C.B.A.D.C.
二、填空题
11.
12. , , ,或.
13.12.
14.12.
15.
16.6.
17.,.
18..
三、解答题
19.解:∵DE∥BC
∴ AE:EC=2:3=AD:BD
设AD=2k,BD=3k,则k=3
∴AD=6,BD=9
20.∵AD∥EB∥FC,
∴EC:AC= BF:DF,
∴EC:12=7:10,
∴EC=.
21.解:(1)∵ADBECF,
∴,
∵AB=6,BC=8,
∴,
故的值为;
(2)如图,过点A作AGDF交BE于点H,交CF于点G,
∵AGDF,ADBECF,
∴AD=HE=GF=5,
∵CF=19,
∴CG=CF-GF=14,
∵BECF,
∴,
∴,
解得BH=6,
∴BE=BH+HE=11.
22.解:(1)∵DE∥BC,且AD=2BD
∴
(2)∵DE∥BC,且AD=2BD
∴
∵AE=5
∴AC=
23.∵FE∥CD,
∴,
∵AD是线段AF与AB的比例中项,
∴,
∴,
∴DE∥BC.
24.解:(1)∵DE∥BC,
∴,
又,AE=3,
∴,
解得AC=9,
∴EC=AC-AE=9-3=6;
(2)∵DE∥BC,EF∥CG,
∴,
∴AD AG=AF AB.
第二课时答案
一、单选题
A.B.A.B.B.C.C.D.
二、填空题
9..
10.
11..
12. .
13.5:3:2.
14.400.
三、解答题
15.解:作DH∥AC交BE于H,如图,
∵DH∥CE,
∴,
∴CE=2DH,
∵DH∥AE,
∴,
∴AE=DH,
∴.
16.(1)证明:∵,∴,.
∵,∴.
∴.
(2)∵,,.∴
∴,∴.
∴
∵,∴.
17.解:如解图,过点作的平行线,过点作的平行线相交于点,延长交于点.
∵,,
∴四边形为正方形,
∴,
∴,
又∵,
∴,
∴,
又∵,
∴,
∴.
又∵,
∴.
18.解:(1)设S△BDE=x.
∵,
∵DE∥BC,
∴,
∴
∵S△ADE=2,S△BCE=7.5,
∴,
解得:x1=﹣5(舍),x2=3.经检验x=3是此题的解,
∴S△BDE=3;
(2)由(1)知,
设S△ADE=y,又S△BDE=m,S△BCE=n,
∴,
解得,
∴.
19.证明:∵ AD是边BC上的中线,∴ BD = DC.
∵ HF∥AB,∴ ,
∴ ,
即,
∵ EG∥AC,∴ ,
∴ ,
∴ HF = BG,
又∵ HF∥BG,∴ 四边形BGFH是平行四边形,
∴ GF = BH.
20.解(1)∵,
∴,即,
∴,
∴.
(2)∵平移AB使得A与H重合,
∴,.
∵,,∴四边形DECF为平行四边形,
∴.∵,∴
即,∴.
(3)∵的面积和四边形FCED的面积相等,
,
∴,∴,又∵,
∴四边形BDEF为平行四边形,,
∴,,
,
即这个相等的面积为6.
21.解:(1)∵HI∥AD,
∴,
∴,
∴AD=6,
∴ID=CD﹣CI=2,∴正方形的边长为2;
(2)三角形,理由如下:
如图2中,设点G落在PC时对应的点为G′,点F的对应的点为F′.
∵CA=CP,CD⊥PA,∴∠ACD=∠PCD,∠A=∠P,
∵HG′∥PA,
∴∠CHG′=∠A,∠CG′H=∠P,
∴∠CHG′=∠CG′H,∴CH=CG′,
∴IH=IG′==DF′=3,
∵IG∥DB,∴,
∴,∴DB=3,
∴DB=DF′=3,∴点B与点F′重合,
∴移动后的矩形与△CBP重叠部分是△BGG′,
∴移动后的矩形与△CBP重叠部分的形状是三角形;
(3)如图3中,如图将△DMI′绕点D逆时针旋转90°得到△DF′R,此时N、F′、R共线.
∵∠MDN=∠NDF+∠MDI′=∠NDF′+∠DF′R=∠NDR=45°,
∵DN=DN,DM=DR,
∴△NDM≌△NDR,
∴MN=NR=NF′+RF′=NF′+MI′,
∴△MNG′的周长=MN+MG′+NG′=MG′+MI′+NG′+F′R=2I′G′=4.
第一课时
一、单选题
1.如图,在△ABC中,DEBC,若,则等于( )
A. B. C. D.
2.如图,AB∥CD,AD与BC交于点O,则下列比例式中正确的是( )
A. B. C. D.
3.中,直线交于,交于点,那么能推出的条件是( )
A. B. C. D.
4.如图,已知:AB、CD相交于点O,由下列哪一组条件可以推出AC∥BD( )
A., B.
C. D.
5.如图,已知直线a//b//c,直线m分别交直线a,b,c于点A,B,C;直线n分别交直线a,b,c于点D,E,F.若,则=( )
A. B. C. D.1
6.如图,点A,E,F,C在同一条直线上,,BE的延长线交AD于点G,且,则下列结论中错误的是( )
A.= B.= C.= D.=
7.如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
A. B.
C. D.
8.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D、E、F,AC与DF相交于点H,且AH=2,HB=1,BC=5,则( )
A. B.2 C. D.
9.如图,在中,,两边上的中线,相交于点,则( )
A. B. C. D.
10.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,已知,、交于点,若,则______.
12.如图,已知,则______,______,______,______.
13.如图,,如果,那么________.
14.如图,在中,是中线,是重心,过点作,分别交、于点、,若,则____________.
15.如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则 的值是_____.
16.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=1,则AD=_____.
17.如图,已知,,则______,______.
18.如图,在中,为边上的中线,是的角平分线,交于点F.则的长为______.
三、解答题
19.如图,在△ABC中,DE∥BC,分别与AB、AC交于点D、E,若AE:EC=2:3,DB-AD=3,求AD和DB的长.
20.如图,已知AD∥EB∥FC,AC=12,DB=3,BF=7,求EC的长.
21.如图,已知ADBECF,它们依次交直线、于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
22.如图,在△ABC中,DE∥BC,分别与AB、AC交于点D、E,点F在BC上,DE交AF于点G,AD=2BD,AE=5,求:(1);(2)AC的长.
23.如图,在△ABC中,点D、F是在边AB 上,点E在边AC上,且FE∥CD,线段AD是线段AF与AB的比例中项.
求证:DE∥BC
24.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
第二课时
一、单选题
1.如图,在△ABC中,点D在边BC上,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.; B.; C.; D..
2.如图,在中,D是上一点,连接是的中点,连接并延长交于点E,则的值为( )
A. B. C. D.
3.在中,D.F.E分别在边BC.AB.AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
A. B. C. D.
4.如图,在中,,,已知,则的长是
A. B.3 C. D.4
5.如图,,与相交于点,过点的直线交于点,交于点.若,,,则的长为( )
A. B. C. D.4
6.如图,在中,点,点为边的三等分点,与交于点,则下列比例式正确的是( )
A. B. C. D.
7.如图,在△ABC中,M是AC的中点,P,Q为BC边上的点,且BP=PQ=CQ,BM与AP,AQ分别交于D,E点,则BD∶DE∶EM等于
A.3∶2∶1 B.4∶2∶1 C.5∶3∶2 D.5∶2∶1
8.在中,、是边上的三等分点,是边上的中线,、分为三段的长分别是、、,若这三段有,则等于( )
A. B. C. D.
二、填空题
9.如图,的中线、交于点,点在边上,,那么的值是__________.
10.如图,直线,且每相邻两条直线的距离相等.若直线分别与相交于点,则为___________.
11.如图,在中,为上一点,且,过点作交于点,连接,过点作交于点.若,则______.
12.如图,在中,点是边的中点,直线交边于点,交的延长线于点,如果,那么的值为____.(用含、的式子表示)
13.如图中,、为的三等份点,为的中点,与、分别交于、,则________.
14.如图,在中,,.在边上有个不同的点,,,¨¨¨¨,,过这个点分别作的内接矩形,,¨¨¨¨,,设每个矩形的周长分别为,,¨¨¨¨,,则¨¨¨¨________.
三、解答题
15.如图,中,是中线,点在上,且,的延长线交于,求的值.
16.如图,MN经过ABC的顶点A,MN∥BC,AM=AN,MC交AB于D,NB交AC于E.
(1)求证:DE∥BC;
(2)联结DE,如果DE=1,BC=3,求MN的长.
17.如图,在中,,,点为边上的中点,连接,过点作于点,延长交于点,求的值.
18.如图,点D、E分别在△ABC的边AB、AC上,DEBC.
(1)若S△ADE=2,S△BCE=7.5,求S△BDE;
(2)若S△BDE=m,S△BCE=n,求S△ABC(用m、n表示).
19.已知:如图,在△ABC中,AD是边BC上的中线,点E在线段DC上,EF∥AB交边AC于点F,EG∥AC交边AB于点G,FE的延长线与AD的延长线交于点H.
求证:GF = BH.
20.如图(1),,直线AB和CH交于点O,分别交于D、E两点,已知,,.
(1)尝试探究:在图(1)中,求DB和AD的长;
(2)类比延伸:平移AB使得A与H重合,如图(2)所示,过点D作,若,求线段BF的长;
(3)拓展迁移:如图(3),若的面积是10,点D、E分别位于AB、CA上,,点F在BC上且,,如果的面积和四边形FCED的面积相等,求这个相等的面积.
21.如图1.在△ABC中,矩形EFGH的一边EF在AB上,顶点G、H分别在BC、AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD.矩形DFGI恰好为正方形.
(1)求正方形DFGI的边长;
(2)如图2,延长AB至P.使得AC=CP,将矩形EFGH沿BP的方向向右平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?
(3)如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG、DB相交于点M、N,求△MNG′的周长.
第一课时答案
一、单选题
C.D.C.C.A.C.B.A.D.C.
二、填空题
11.
12. , , ,或.
13.12.
14.12.
15.
16.6.
17.,.
18..
三、解答题
19.解:∵DE∥BC
∴ AE:EC=2:3=AD:BD
设AD=2k,BD=3k,则k=3
∴AD=6,BD=9
20.∵AD∥EB∥FC,
∴EC:AC= BF:DF,
∴EC:12=7:10,
∴EC=.
21.解:(1)∵ADBECF,
∴,
∵AB=6,BC=8,
∴,
故的值为;
(2)如图,过点A作AGDF交BE于点H,交CF于点G,
∵AGDF,ADBECF,
∴AD=HE=GF=5,
∵CF=19,
∴CG=CF-GF=14,
∵BECF,
∴,
∴,
解得BH=6,
∴BE=BH+HE=11.
22.解:(1)∵DE∥BC,且AD=2BD
∴
(2)∵DE∥BC,且AD=2BD
∴
∵AE=5
∴AC=
23.∵FE∥CD,
∴,
∵AD是线段AF与AB的比例中项,
∴,
∴,
∴DE∥BC.
24.解:(1)∵DE∥BC,
∴,
又,AE=3,
∴,
解得AC=9,
∴EC=AC-AE=9-3=6;
(2)∵DE∥BC,EF∥CG,
∴,
∴AD AG=AF AB.
第二课时答案
一、单选题
A.B.A.B.B.C.C.D.
二、填空题
9..
10.
11..
12. .
13.5:3:2.
14.400.
三、解答题
15.解:作DH∥AC交BE于H,如图,
∵DH∥CE,
∴,
∴CE=2DH,
∵DH∥AE,
∴,
∴AE=DH,
∴.
16.(1)证明:∵,∴,.
∵,∴.
∴.
(2)∵,,.∴
∴,∴.
∴
∵,∴.
17.解:如解图,过点作的平行线,过点作的平行线相交于点,延长交于点.
∵,,
∴四边形为正方形,
∴,
∴,
又∵,
∴,
∴,
又∵,
∴,
∴.
又∵,
∴.
18.解:(1)设S△BDE=x.
∵,
∵DE∥BC,
∴,
∴
∵S△ADE=2,S△BCE=7.5,
∴,
解得:x1=﹣5(舍),x2=3.经检验x=3是此题的解,
∴S△BDE=3;
(2)由(1)知,
设S△ADE=y,又S△BDE=m,S△BCE=n,
∴,
解得,
∴.
19.证明:∵ AD是边BC上的中线,∴ BD = DC.
∵ HF∥AB,∴ ,
∴ ,
即,
∵ EG∥AC,∴ ,
∴ ,
∴ HF = BG,
又∵ HF∥BG,∴ 四边形BGFH是平行四边形,
∴ GF = BH.
20.解(1)∵,
∴,即,
∴,
∴.
(2)∵平移AB使得A与H重合,
∴,.
∵,,∴四边形DECF为平行四边形,
∴.∵,∴
即,∴.
(3)∵的面积和四边形FCED的面积相等,
,
∴,∴,又∵,
∴四边形BDEF为平行四边形,,
∴,,
,
即这个相等的面积为6.
21.解:(1)∵HI∥AD,
∴,
∴,
∴AD=6,
∴ID=CD﹣CI=2,∴正方形的边长为2;
(2)三角形,理由如下:
如图2中,设点G落在PC时对应的点为G′,点F的对应的点为F′.
∵CA=CP,CD⊥PA,∴∠ACD=∠PCD,∠A=∠P,
∵HG′∥PA,
∴∠CHG′=∠A,∠CG′H=∠P,
∴∠CHG′=∠CG′H,∴CH=CG′,
∴IH=IG′==DF′=3,
∵IG∥DB,∴,
∴,∴DB=3,
∴DB=DF′=3,∴点B与点F′重合,
∴移动后的矩形与△CBP重叠部分是△BGG′,
∴移动后的矩形与△CBP重叠部分的形状是三角形;
(3)如图3中,如图将△DMI′绕点D逆时针旋转90°得到△DF′R,此时N、F′、R共线.
∵∠MDN=∠NDF+∠MDI′=∠NDF′+∠DF′R=∠NDR=45°,
∵DN=DN,DM=DR,
∴△NDM≌△NDR,
∴MN=NR=NF′+RF′=NF′+MI′,
∴△MNG′的周长=MN+MG′+NG′=MG′+MI′+NG′+F′R=2I′G′=4.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
