数据的波动[上学期]

课件13张PPT。八年级数学（下册）第五章 数据的收集与处理4 数据的波动(1)收集数据＿随机抽样：
广泛性＿被调查的对象不得太少;
代表性＿被调查的对象随意抽取的，没有人为的因素;
真实性＿调查的数据是真实的.总体与个体抽样与样本为了一定的目的而对考察对象进行全面调查，称为普查，其中所考察对象的全体称为总体(population)，而组成总体的每一个考察对象称为个体(individual).从总体中抽取部分个体进行调查，这种调查称为抽样调查(sampling investigation),其中从总体中抽取部分个体叫做总体的一个样本(sample).数据的代表平均数：一般地，对于n个数x1,x2,……,xn,我们把(x1+x2+……+xn)÷n叫做这个数的平均数(mean),简称平均数.
中位数:一般地,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数(median).
众数:一组数据中出现次数最多的那个数据叫做这组数据的众数(mode).
平均数,中位数和众数都是数据的代表,它们刻画了一组数据的“平均水平”. 频数与频率我们称每个考查对象出现的次数为频数(absolute frequency),
每个对象出现的次数与总次数的比值为频率(relative frequency).
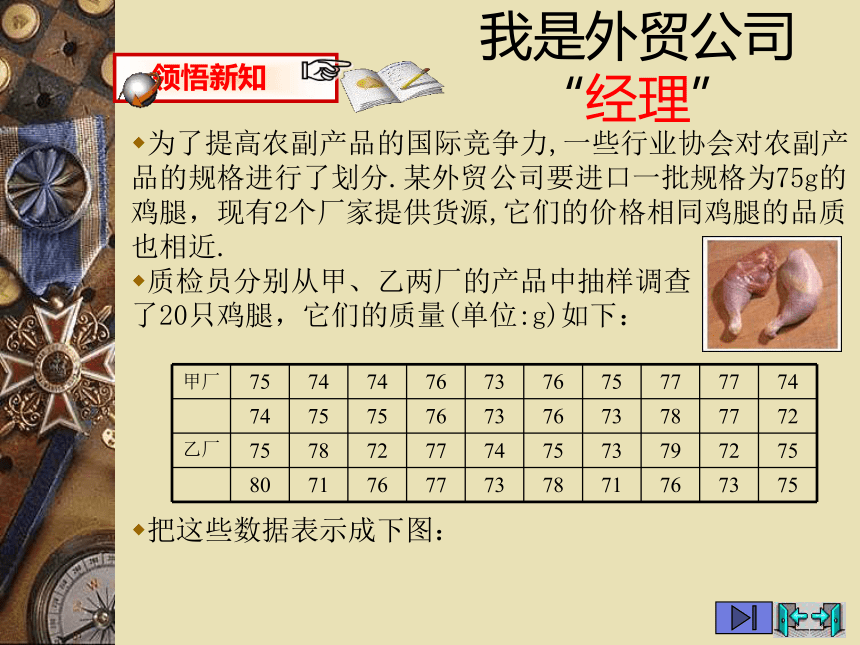
频数、频率、频数分布表、频数分布直方图和频数分布折线图都反映了一组数据的分布情况.我是外贸公司“经理”为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分.某外贸公司要进口一批规格为75g的鸡腿，现有2个厂家提供货源,它们的价格相同鸡腿的品质也相近.
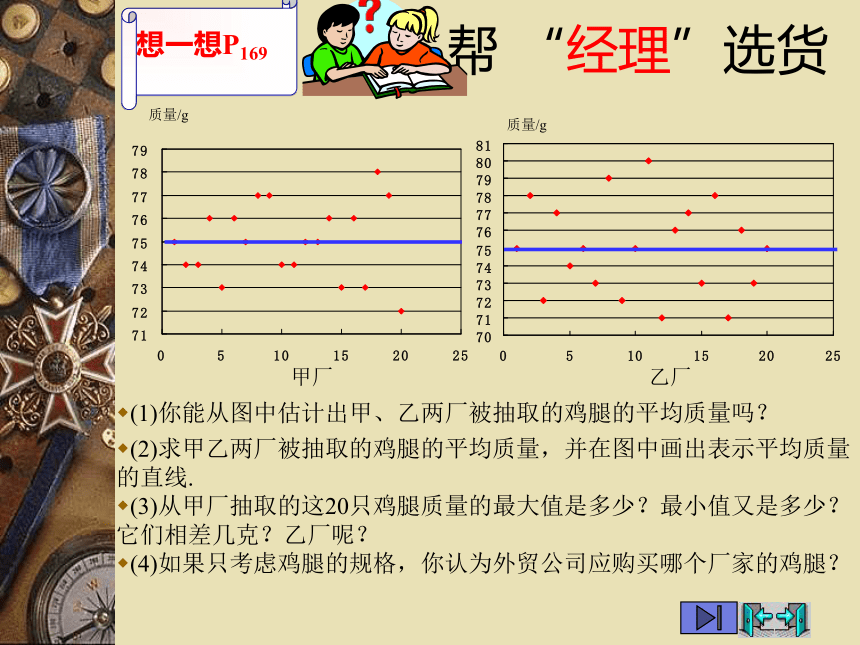
质检员分别从甲、乙两厂的产品中抽样调查　　　　　了20只鸡腿，它们的质量(单位:g)如下：把这些数据表示成下图：帮 “经理”选货(1)你能从图中估计出甲、乙两厂被抽取的鸡腿的平均质量吗？(2)求甲乙两厂被抽取的鸡腿的平均质量，并在图中画出表示平均质量的直线.(3)从甲厂抽取的这20只鸡腿质量的最大值是多少？最小值又是多少？它们相差几克？乙厂呢？(4)如果只考虑鸡腿的规格，你认为外贸公司应购买哪个厂家的鸡腿？一图知“情”实际生活中,除了关心数据的“平均水平”外,人们往往还关注数据的离散程度,即它们相对于“平均水平”的偏离情况.极差就是刻画数据的离散程度的一个统计量.极差是指一组数据中最大数据与最小数据的差.(3)在甲、丙两厂中你认为那个厂的鸡腿质量更符合要求?为什么？市场竞争如果丙厂也参与了竞争，从该厂抽样调查了20鸡腿，数据如下图所示：(1)丙厂这20只鸡腿质量的平均数和极差分别是多少？(2)如何刻画丙厂这20只鸡腿质量与其平均数的差距？分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.一数知“情”数学上，数据的离散程度还可以用方差或标准差来刻画.方差（variance）是各个数据与平均数之差的平方的平均数,即一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.展现自我 甲乙两支仪仗队队员的身高（单位：cm）如下：甲、乙两支仪仗队队员的身高的平均数都是178cm,极差分别是2cm、4cm,方差分别是0.6、1.8,可以认为，甲仪仗队更为整齐一些.哪支依仗队更为整齐？你是怎么判断的？回味无穷数理统计的基本思想：
用样本估计总体.
用样本的某些特性估计总体相应的特性.
用样本的平均数、中位数和众数去估计相应总体的平均水平特性.
用样本的频数、频率、频数分布表、频数分布直方图和频数分布折线图去估计相应总体数据的分布情况.
用样本的极差、方差或标准差去估计相应总体数据的波动情况.知识的升华P172习题5.5 1,2题;
祝你成功！结束寄语最好的应用数学是与最好的纯数学同样深奥、美妙和有趣.
在学习和生活中体会数学的“简捷”性.