11.2.1 三角形的内角 课件(共28张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-24 20:30:07 | ||
图片预览



文档简介
(共28张PPT)
11.2 与三角形有关的角
11.2.1 三角形的内角
第十一章 三角形
人教版数学教材 八年级上
学习目标
1.了解三角形内角和的证明思路.
2.会用三角形的内角和定理解决简单的实际问题.
重点:三角形的内角和定理及其应用.
难点:三角形的内角和证明及其应用.
课前预习
阅读课本P11-14页内容,了解本节主要内容.
180°
直角三角形
互余
新课导入
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
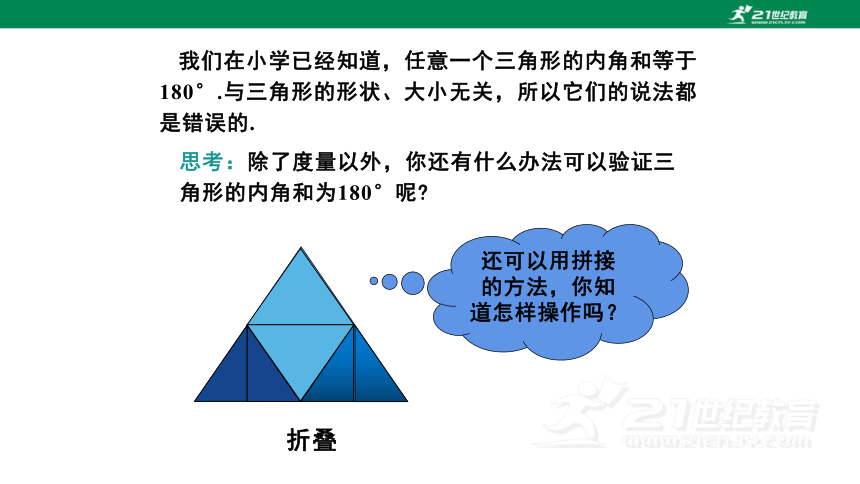
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关,所以它们的说法都是错误的.
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢
折叠
还可以用拼接的方法,你知道怎样操作吗?
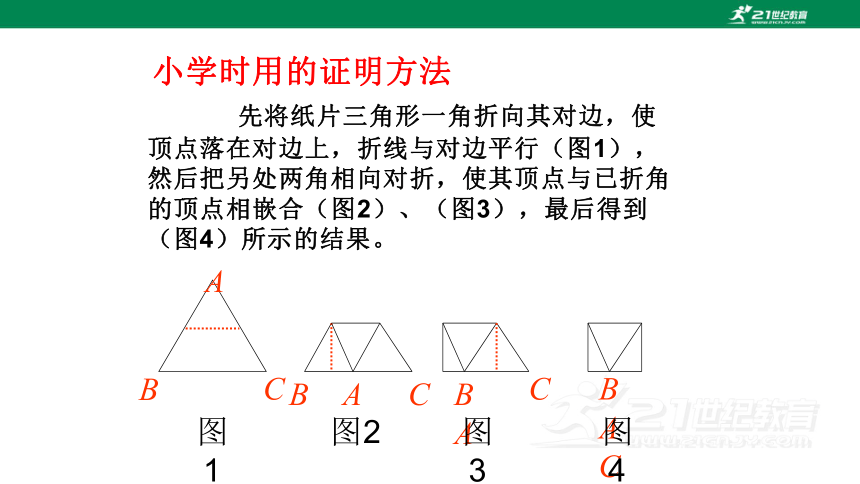
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
小学时用的证明方法
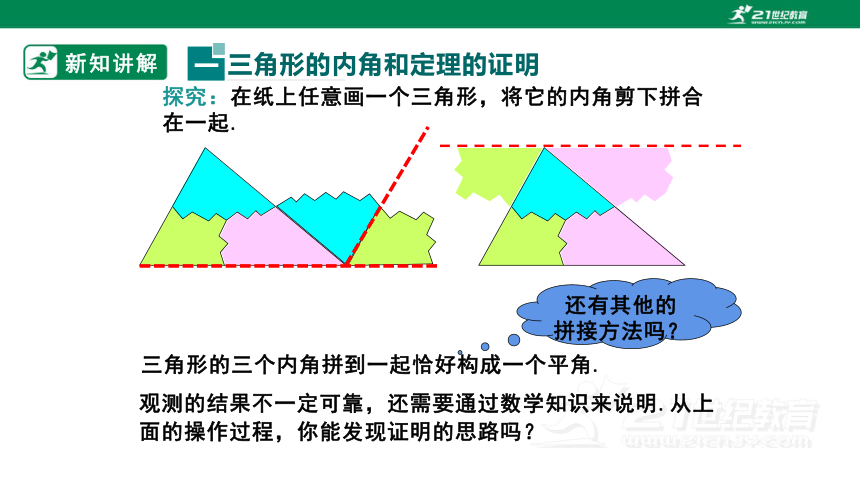
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
还有其他的拼接方法吗?
三角形的内角和定理的证明
一
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
新知讲解
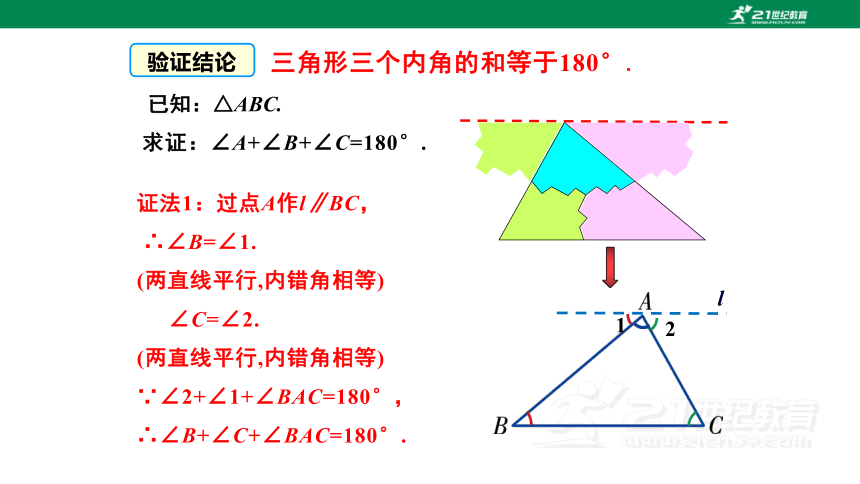
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
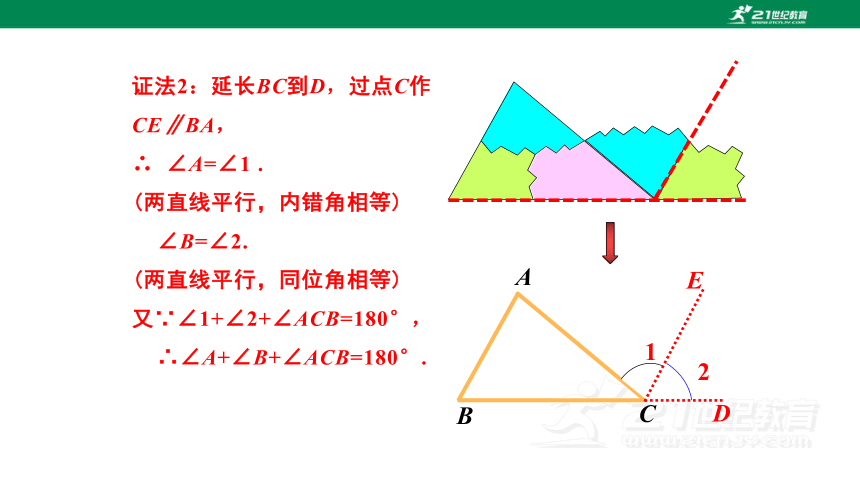
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,∴∠A+∠B+∠C=180°.
想一想:同学们还有其他的方法吗?
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
新知讲解
北
.
A
D
北
.
C
B
东
E
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
三角形的内角和定理也常常用在实际问题中.
解: ∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °- ∠BAD=180°-80°=100°,
∠ABC= ∠ABE- ∠EBC=100°-40°=60°.
在△ABC中,
∠ACB=180 °- ∠ABC- ∠ CAB
=180°-60°-30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°.
北
.
A
D
北
.
C
B
东
E
问题1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度
30°+60°=90°
45°+45°=90°
直角三角形的两个锐角互余
三
问题引导
新知讲解
问题2:如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=90°,即
∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
A
B
C
直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt △ABC .
总结归纳
方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.
例3(1)如图 ,∠B=∠C=90°,AD交BC于点O,∠A
与∠D有什么关系?
图
典例分析
问题3:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形
四
新知讲解
A
B
C
应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
归纳总结
例4 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三
角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+ ∠A=90 °.
∵ ∠1= ∠2,
∴∠1 + ∠A=90 °.
即△ADE是直角三角形.
典例分析
1.求出下列各图中的x值.
x=70
x=60
x=30
x=50
随堂练习
2.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
90°
3.如图,AB、CD相交于点O,AC⊥CD于点C,
若∠BOD=38°,则∠A=________.
52°
第2题图
第3题图
4.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
直角三角形
5. 如图,四边形 ABCD 中,点 E 在 BC 上,∠A +∠ADE = 180°,∠B = 78°,∠C = 60°,求∠EDC 的度数.
解:∵∠A +∠ADE = 180°,
∴ AB∥DE.
∴∠CED =∠B = 78°.
又∵∠C = 60°,
∴∠EDC = 180° - (∠CED +∠C )
= 180° - (78°+ 60°) = 42°.
6. 如图,在△ABC 中,∠B = 42°,∠C = 78°,AD 平分∠BAC.求∠ADC 的度数.
解:∵∠B = 42°,∠C = 78°,
∴∠BAC = 180° - ∠B - ∠C = 60°.
∵ AD 平分∠BAC,
∴∠CAD = ∠BAC = 30°.
∴∠ADC = 180° - ∠C - ∠CAD = 72°.
7.如图,在△ABC 中,BP 平分∠ABC,CP 平分∠ACB.
(1)若∠A = 60°,求∠BPC 的度数.
解:在△ABC 中,∵∠A = 60°,
∴∠ABC +∠ACB = 120°.
∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB) = 60°.
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - 60° = 120°.
(2) 你能直接写出∠BPC 与∠A 之间的数量关系吗?
解:∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB).
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - (∠ABC +∠ACB)
= 180° - (180° - ∠A)
= 90° + ∠A.
三角形的内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
直角三角形的性质与判定
性质
判定
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
课堂小结
本课结束
*
*
11.2 与三角形有关的角
11.2.1 三角形的内角
第十一章 三角形
人教版数学教材 八年级上
学习目标
1.了解三角形内角和的证明思路.
2.会用三角形的内角和定理解决简单的实际问题.
重点:三角形的内角和定理及其应用.
难点:三角形的内角和证明及其应用.
课前预习
阅读课本P11-14页内容,了解本节主要内容.
180°
直角三角形
互余
新课导入
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关,所以它们的说法都是错误的.
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢
折叠
还可以用拼接的方法,你知道怎样操作吗?
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
小学时用的证明方法
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
还有其他的拼接方法吗?
三角形的内角和定理的证明
一
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
新知讲解
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,∴∠A+∠B+∠C=180°.
想一想:同学们还有其他的方法吗?
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
新知讲解
北
.
A
D
北
.
C
B
东
E
例2 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
三角形的内角和定理也常常用在实际问题中.
解: ∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °.
所以∠ABE=180 °- ∠BAD=180°-80°=100°,
∠ABC= ∠ABE- ∠EBC=100°-40°=60°.
在△ABC中,
∠ACB=180 °- ∠ABC- ∠ CAB
=180°-60°-30° =90°,
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°.
北
.
A
D
北
.
C
B
东
E
问题1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度
30°+60°=90°
45°+45°=90°
直角三角形的两个锐角互余
三
问题引导
新知讲解
问题2:如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=90°,即
∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
A
B
C
直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt △ABC .
总结归纳
方法一(利用平行的判定和性质):
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质):
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.
例3(1)如图 ,∠B=∠C=90°,AD交BC于点O,∠A
与∠D有什么关系?
图
典例分析
问题3:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形
四
新知讲解
A
B
C
应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
归纳总结
例4 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三
角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+ ∠A=90 °.
∵ ∠1= ∠2,
∴∠1 + ∠A=90 °.
即△ADE是直角三角形.
典例分析
1.求出下列各图中的x值.
x=70
x=60
x=30
x=50
随堂练习
2.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
90°
3.如图,AB、CD相交于点O,AC⊥CD于点C,
若∠BOD=38°,则∠A=________.
52°
第2题图
第3题图
4.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
直角三角形
5. 如图,四边形 ABCD 中,点 E 在 BC 上,∠A +∠ADE = 180°,∠B = 78°,∠C = 60°,求∠EDC 的度数.
解:∵∠A +∠ADE = 180°,
∴ AB∥DE.
∴∠CED =∠B = 78°.
又∵∠C = 60°,
∴∠EDC = 180° - (∠CED +∠C )
= 180° - (78°+ 60°) = 42°.
6. 如图,在△ABC 中,∠B = 42°,∠C = 78°,AD 平分∠BAC.求∠ADC 的度数.
解:∵∠B = 42°,∠C = 78°,
∴∠BAC = 180° - ∠B - ∠C = 60°.
∵ AD 平分∠BAC,
∴∠CAD = ∠BAC = 30°.
∴∠ADC = 180° - ∠C - ∠CAD = 72°.
7.如图,在△ABC 中,BP 平分∠ABC,CP 平分∠ACB.
(1)若∠A = 60°,求∠BPC 的度数.
解:在△ABC 中,∵∠A = 60°,
∴∠ABC +∠ACB = 120°.
∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB) = 60°.
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - 60° = 120°.
(2) 你能直接写出∠BPC 与∠A 之间的数量关系吗?
解:∵ BP 平分∠ABC,CP 平分∠ACB,
∴∠PBC +∠PCB = (∠ABC +∠ACB).
∵∠PBC +∠PCB +∠BPC = 180°,
∴∠BPC = 180° - (∠ABC +∠ACB)
= 180° - (180° - ∠A)
= 90° + ∠A.
三角形的内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
直角三角形的性质与判定
性质
判定
直角三角形的两个锐角互余
有两个角互余的三角形是直角三角形
课堂小结
本课结束
*
*
