安徽省定远重点中学2022-2023学年下学期九年级6月最后一卷数学试题(PDF版,含解析)
文档属性
| 名称 | 安徽省定远重点中学2022-2023学年下学期九年级6月最后一卷数学试题(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 09:58:35 | ||
图片预览




文档简介
定远重点中学 2022-2023 学年下学期九年级 6 月最后一卷
数学试题
第 I 卷(选择题)
一、选择题(本大题共 10 小题,共 40 分。在每小题列出的选项中,选出符合题目的一项)
1. 1分数4的相反数是( )
A. 14 B.
1
4 C. 4 D. ±
1
2
2. 一个立体图形的三视图如图所示,则该立体图形是( )
A. 圆柱
B. 圆锥
C. 长方体
D. 三棱柱
3. 下列计算正确的是( )
A. 2 3 = 6 B. (3 )2 = 6 2 C. 6 ÷ 3 = 2 D. 3 2 2 = 2 2
4. 1在数轴上表示不等式 2 < 0的解集,正确的是 ( )
A. B.
C. D.
5. 下列函数中, 的值随 值的增大而减小的是 ( )
A. = 2 + 1 B. = 2 + 1 C. = 2 + 1 D. = 2 + 1
6. 如图, 是⊙ 的直径,点 、 在⊙ 上,∠ = 30°,则∠ 的大小为( )
A. 150°
B. 130°
C. 120°
D. 60°
7. 若关于 的二次函数 = 2 3 + 的图象与 轴有两个交点,
且 ≥ 3,则从满足条件的所有整数 中随机选取一个,恰好是负数的概率是( )
A. 1 B. 13 2 C.
2
3 D.
5
6
8. 如图,正方形 的边长为 5,点 在 边上, = 2,连接 ,将△ 沿 翻折
得△ ′ ,延长 ′交 于点 .则 ′ 的长度为( )
A. 2
B. 94
C. 157
D. 3 2 2
9. 已知二次函数 = 2 + + 和一次函数 = + ,
则这两个函数在同一个平面直角坐标系中的大致图象是( )
A. B.
C. D.
10. 如图,正方形 的面积为 3,点 在边 上,且 = 1,∠ 的平分线交 于点 ,
点 , 分别是 , 的中点,则下列结论正确的有( )
① = ② = 6 22
③ △ 的面积是 1 ④ △ ≌△ ⑤∠ = 30°
A. 2个 B. 3个 C. 4个 D. 5个
第 II 卷(非选择题)
二、填空题(本大题共 4 小题,共 20 分)
11. ( 9)2的平方根是 ,64的立方根是 ,则 + = ______ .
12. “新冠”疫情肆虐全球,打疫苗是最有效的防护措施,据统计数据预测,2021年国药
中生北京公司年新冠病毒灭活疫苗产能和科兴中维二期年新冠病毒灭活疫苗产能之和将超
1600000000剂,用科学记数法表示 1600000000为______ .
13. 如图, 为钝角△ 中 边的中点,经过 的直线 将△ 分成了周长相等的两
部分,已知 = 8,∠ = 120°,则 = ______ .
14. 如图, 、 是双曲线 = ( < 0)上两点,连接 、
,过点 作 ⊥ 轴于点 ,交线段 于点 ,若△
的面积是 1, = 2 ,则 = ______ .
三、解答题(本大题共 9 小题,共 90 分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题 8分)
2( 1) ≥ 3
(1)解不等式组: 3 +4 > 并在数轴上表示解集.5
2
(2)先化简,再求值:(1 + 1 ) ÷ 1,其中 = 2 + 1.
16. (本小题 8分)
为响应乡村振兴号召,在外地创业成功的大学毕业生小姣毅然返乡当起了新农人,创办了果
蔬生态种植基地.最近,为给基地蔬菜施肥,她准备购买甲、乙两种有机肥.已知甲种有机肥每
吨的价格比乙种有机肥每吨的价格多 100元,购买 2吨甲种有机肥和 1吨乙种有机肥共需
1700元.甲、乙两种有机肥每吨各多少元?
17. (本小题 8分)
图①、图②、图③均是 6 × 6的正方形网格,每个小正方形的边长均为 1,其顶点称为格点,
△ 的顶点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作
图痕迹.
(1)在图①中确定一点 ,使四边形 是平行四边形;
(2)在图②中,在边 上确定一点 ,使 ⊥ ;
(3)在图③中确定一点 ,使△ 与△ 关于 对称.
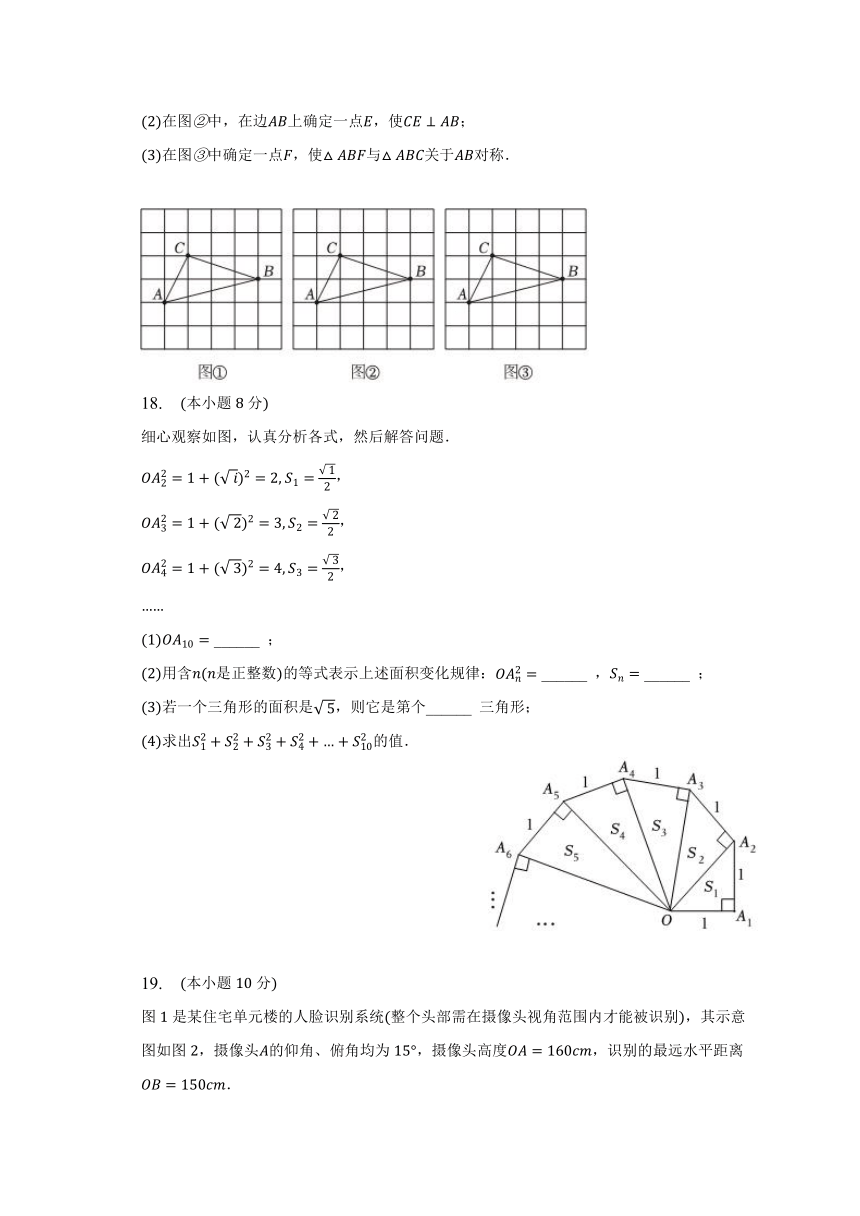
18. (本小题 8分)
细心观察如图,认真分析各式,然后解答问题.
22 = 1 + ( )2 = 2, =
1
1 ,2
23 = 1 + ( 2)2 = 3, 2 =
2,
2
24 = 1 + ( 3)2 = 4,
3
3 = ,2
……
(1) 10 = ______ ;
(2)用含 ( 是正整数)的等式表示上述面积变化规律: 2 = ______ , = ______ ;
(3)若一个三角形的面积是 5,则它是第个______ 三角形;
(4)求出 21 + 22 + 23 + 2 24 + … + 10的值.
19. (本小题 10分)
图 1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意
图如图 2,摄像头 的仰角、俯角均为 15°,摄像头高度 = 160 ,识别的最远水平距离
= 150 .
(1)身高 208 的小杜,头部高度为 26 ,他站在离摄像头水平距离 130 的点 处,请问
小杜最少需要下蹲多少厘米才能被识别?
(2)身高 120 的小若,头部高度为 15 ,踮起脚尖可以增高 3 ,但仍无法被识别,社区
及时将摄像头的仰角、俯角都调整为 20°(如图 3),此时小若能被识别吗?请计算说明.
(精确到 0.1 ,参考数据: 15° ≈ 0.26, 15° ≈ 0.97, 15° ≈ 0.27, 20° ≈ 0.34,
20° ≈ 0.94, 20° ≈ 0.36)
20. (本小题 10分)
如图, 是半圆 的直径, 是半圆 上的一点(不与 , 重合),连接 ,点 为弧 的中
点,过点 作 ⊥ ,交 的延长线于点 .
(1)求证: 是半圆 的切线;
(2)若 = 6, = 4 3,求阴影部分的面积.
21. (本小题 12分)
为贯彻落实党的二十大关于深化全民阅读活动的重要部署,教育部印发了《全国青少年学生
读书行动实施方案》,于是某中学开展了以“书香润校园,好书伴成长”为主题的系列读书
活动.学校为了解学生周末的阅读情况,采用随机抽样的方式获取了若干名学生的周末阅读时
间数据,整理后得到下列不完整的图表:
类别 类 类 类 类
阅读时长 (小时) 0 ≤ < 1 1 ≤ < 2 2 ≤ < 3 ≥ 3
频数 8 4
请根据图表中提供的信息解答下面的问题:
(1)此次调查共抽取了______ 名学生, = ______ , = ______ ;
(2)扇形统计图中, 类所对应的扇形的圆心角是______ 度;
(3)已知在 类的 4名学生中有两名男生和两名女生,若从中随机抽取两人参加阅读分享活动,
请用列表或画树状图的方法求出恰好抽到一名男生和一名女生的概率.
22. (本小题 12分)
如图,已知:以 △ 的边 为直径作△ 的外接圆⊙ ,∠ 的平分线 交 于 ,交
⊙ 于 ,过 作 / / 交 的延长线于 . = 5, = 10,
(1)求证: 是⊙ 切线;
(2)求⊙ 的半径长;
(3)求 sin∠ 的值.
23. (本小题 14分)
如图,二次函数 = 2 + + 经过点 (4,0)、 (0,2),点 是 轴正半轴上一个动点,过点
作垂直于 轴的直线分别交抛物线和直线 于点 和点 .设点 的横坐标为 .
(1)求二次函数的表达式;
(2)若 、 、 三个点中恰有一点是其它两点所连线段的中点(三点重合除外)时,求 的值.
(3)点 在线段 上时,若以 、 、 为顶点的三角形与△ 相似,求 的值.
答案和解析
1.【答案】
1 1
【解析】分数4的相反数是 4.故选: .
2.【答案】
【解析】根据主视图和左视图为矩形判断出是柱体,
根据俯视图是三边形可判断出这个几何体应该是三棱柱.故选: .
3.【答案】
【解析】解: 、 2 3 = 2+3 = 5,原式计算错误,故选项不符合题意;
B、(3 )2 = 9 2,原式计算错误,故选项不符合题意;
C、 6 ÷ 3 = 6 3 = 3,原式计算错误,故选项不符合题意;
D、3 2 2 = 2 2,计算正确,故选项符合题意.故选: .
4.【答案】
1
【解析】 2 < 0
解得: < 1,
在数轴上表示为: 故选 A.
5.【答案】
【解析】 . = 2 + 1中,当 < 0 时, 的值随 的值增大而减小,不符合题意;
B. = 2 + 1中,当 > 0 时, 的值随 的值增大而减小,不符合题意;
C. = 2 + 1 中, > 0, 的值随 的值增大而增大,不符合题意;
D. = 2 + 1 中, < 0, 的值随 的值增大而减少,符合题意;
故选 D.
6.【答案】
【解析】∵ 是⊙ 的直径,∠ = 30°,
∴ ∠ = 2∠ = 60°,
∴ ∠ = 180° 60° = 120°.故选: .
7.【答案】
【解析】根据题意,关于 的二次函数 = 2 3 + 的图象与 轴有两个交点,则关于 的方程
2 3 + = 0 有两个不相等的实数根,
故该一元二次方程的根的判别式 > 0,即 = ( 3)2 4 × 1 × > 0,
9
解得 < 4,
又∵ ≥ 3,
∴ 3 ≤ < 94,
∴满足条件的所有整数为 3、 2、 1、0、1、2共计 6个,其中负数有 3、 2、 1共计 3个,
∴ 3 1满足条件的所有整数 中随机选取一个,恰好是负数的概率是6 = 2.故选: .
8.【答案】
【解析】如图所示,连接 ,
∵正方形 的边长为 5,
∴ = = 5,∠ = ∠ = ∠ = 90°,
由折叠得, ′ = = = 5, ′ = = 2,∠ ′ = ∠ = 90°,
∴ ∠ = ∠ ′ = 90°, = = 3,
在 △ 和 △ ′ 中,
=
= ′
∴ △ ≌ △ ′ ( ),
∴ = ′ ,
设 ′ = = ,则 = = 5 , = ′ + ′ = + 2,
在 △ 中,由勾股定理得, 2 = 2 + 2(2 + )2 = 32 + (5 )2,
解得, = 157,
15
即 ′ 的长度是 7,
故选: .
9.【答案】
【解析】解: .图象中二次函数 > 0, < 0,一次函数 > 0, > 0,故 A 不符合题意.
B. 图象中二次函数 > 0, > 0,又对称轴在 轴右侧,则 2 > 0,得出 < 0,矛盾,故 B 不符
合题意.
C.图象中二次函数 < 0, > 0,一次函数 < 0, > 0,故 C 符合题意.
D. 图象中二次函数 < 0, < 0,又对称轴在 轴右侧,则 2 > 0,得出 > 0,矛盾,故 D 不符
合题意.故选: .
10.【答案】
【解析】如图:过点 作 ⊥ ,交 于 ,
∵正方形 的面积为 3,
∴ = = = = 3,
∵ = 1,
∴ = 3 1,tan∠ = =
1 = 3,3 3
∴ ∠ = 30°,
∴ ∠ = ∠ ∠ = 60°, = 2 = 2,
∵ 平分∠ ,
∴ ∠ = ∠ = 12∠ = 30°,故⑤正确;
在 △ 中, = 3 = 1,
∴ = = 3 1,
∴ = ,
∴△ 是等腰直角三角形,
∴ = 2 = 2 × ( 3 1) = 6 2,
∴ ≠ ,故①错误,
∵ , 分别是 , 的中点,
∴ 是△ 的中位线,
∴ = 1 = 6 2;故②正确;2 2
∵ 平分∠ , ⊥ ,∠ = 90°,
∴ = = 1,
∴△ = 1的面积 2 × 2 × 1 = 1,故③正确;
∵ = ,∠ = ∠ = 90°, = ,
∴△ ≌△ ( ),故④正确;故选: .
11.【答案】7或 1
【解析】∵ ( 9)2 = 9,
∴ =± 3,
∵ 64的立方根是 4,
∴ = 4,
∴ + = 3 + 4 = 7 或 + = 3+ 4 = 1,
故答案为:7或 1.
12.【答案】1.6 × 109
【解析】1600000000 = 1.6 × 109.故答案为:1.6 × 109.
13.【答案】4
【解析】如图,延长 到 ,使 = ,连接 .
∵ ∠ = 120°,
∴ ∠ = 180° ∠ = 60°,
∴△ 是等边三角形,
∴ = = = 8.
∵ 为钝角△ 中 边的中点,经过 的直线 将△ 分成了周长相等的两部分,
∴ = , + + = + ,
∴ + = ,
∴ + = ,即 = ,
∵ = ,
∴ 是△ 的中位线,
∴ = 12 = 4.故答案为:4.
14.【答案】 4
【解析】解:如图,过点 作 ⊥ 轴于 ,
∵ ⊥ 轴,
∴ / / ,
∴△ ∽△ ,
∴ = = ,
∵ = 2 ,
∴ =
2
3,
∴ =
2
= 3,
设 = 2 ,则 = 3 ,
∴ ( , 3 ) ( 3 , 2 , 2 ),
∴ = 2 ,
∵△ 的面积是 1,
∴ 1 2 ( 2 ) = 1,
∴ = 4,
故答案为: 4.
2( 1) ≥ 3①
15.【答案】解:(1)解不等式组 3 +4 ,
5 > ②
解不等式①得: ≥ 1,
解不等式②得: < 2,
∴不等式组的解集为: 1 ≤ < 2,
将解集表示在数轴上,如图.
(2) = +1 ÷ ( +1)( 1)原式
= +1 ( +1)( 1)
= 1 1,
当 = 2 + 1时,
1 2
原式= .2+1 1 = 2
16.【答案】解:设甲种有机肥每吨 元,乙种有机肥每吨 元,
= 100
依题意得: 2 + = 1700,
= 600
解得: = 500.
答:甲种有机肥每吨 600元,乙种有机肥每吨 500元.
17.【答案】解:(1)在图①中点 即为所求;
(2)在图②中点 ,即为所求;
(3)在图③中点 即为所求.
【解析】(1)根据平行四边形的性质结合网格,即可求解;
(2)取格点 连接 交 于点 ,则点 即为所求;
(3)作△ 的全等图形△ ,作 / / ,交 的垂线 于点 ,则点 即为所求.
本题考查作图 轴对称变换,平行四边形的判定和性质,学会利用数形结合的思想解决问题是解
题的关键.
18. 10 【答案】 202
【解析】解:(1) 210 = 1 + ( 9)2 = 10,
∴ 10 = 10,
故答案为: 10;
(2) 2 = 1 + ( + 1)2 = ,
( )2 + 1 = + 1,2
=
2 ( 是正整数);
故答案是: ; ;
2
(3) ∵ = 2 = 5,
∴ = 20,
故答案为:20;
(4) 2 2 21 + 2 + 3 + … + 210
= ( 1 )22 + (
2
2 )
2 + ( 32 )
2 + … + ( )22
= 14 (1 + 2 + 3 + … + 10)
= 554.
19.【答案】解:(1)过 作 的垂线分别交仰角、俯角线于点 , ,交水平线于点 ,
在 △ 中,tan∠ = ,
∴ = 15° ≈ 130 × 0.27 = 35.1( ),
∵ = ,∠ = ∠ ,∠ = ∠ = 90°,
∴△ ≌△ ( ),
∴ = = 35.1 ,
∴ = 160 + 35.1 = 195.1( ),
∴小杜最少需要下蹲 208 195.1 = 12.9厘米才能被识别;
(2)如图 2,过 作 的垂线分别交仰角、俯角线于 . .交水平线于 ,
在 △ 中,tan∠ = ,
∴ = 20° ≈ 150 × 0.36 = 54.0( ),
∵ = ,∠ = ∠ ,∠ = ∠ = 90°,
∴△ ≌△ ( ),
∴ = = 54.0 ,
∴ = 160 54.0 = 106.0( ),
∴小若踮起脚尖后头顶的高度为 120 + 3 = 123( ),
∴小若头顶超出点 的高度为:123 106.0 = 17.0( ) > 15 ,
∴踮起脚尖小若能被识别.
20.【答案】(1)证明:∵点 为弧 的中点,
∴ � = � ,
∴ ∠ = ∠ ,
∴ 12∠ =
1
2∠ ,
∵ = ,
∴ ∠ = ∠ = 12∠ ,
∵ ∠ = 12∠ ,
∴ ∠ = ∠ ,
∴ / / ,
∵ ⊥ 交 的延长线于点 ,
∴ ∠ = 90°,
∴ ∠ = 180° ∠ = 90°,
∵ 是⊙ 的半径,且 ⊥ ,
∴ 是半圆 的切线.
(2)解:连接 ,
∵ ∠ = 90°, = 6, = 4 3,
∴ cos∠ = =
6 3
,
4 3 = 2
∴ ∠ = 30°,
∴ ∠ = ∠ = 2∠ = 60°,
∴ ∠ = 180° ∠ ∠ = 60°,
∵ = = ,
∴△ 和△ 都是等边三角形,
∴ = = = = ,
∴四边形 是菱形,
∴ / / ,
∴ ∠ = ∠ = 60°,
∴ ∠ = 90° ∠ = 30°,
∵ = 12 =
1
2 × 4 3 = 2 3,
∴ = 30° = 2 3 × 33 = 2,
∴ = = = 6 2 = 4,
∴ 1 1 1 1△ = △ = 2 = 2 × 4 × 2 3 = 4 3, △ = 2 = 2 × 2 × 2 3 = 2 3,
∵ 阴影 = △ + △ =
60× ×42 8
扇形 , ,扇形 360 = 3
∴ 阴影 = 4 3 + 2 3
8 8
3 = 6 3 3,
∴ 8 阴影部分的面积是 6 3 3.
21.【答案】40 18 10 162
【解析】解:(1)此次调查共抽取的学生人数为:8 ÷ 20% = 40(名),
∴ = 40 × 25% = 10,
∴ = 40 8 10 4 = 18,
故答案为:40,18,10;
(2) 18扇形统计图中, 类所对应的扇形的圆心角是 360° × 40 = 162°,
故答案为:162;
(3)画树状图如下:
共有 12种等可能的结果,其中恰好抽到一名男生和一名女生的结果有 8种,
∴ 8 2恰好抽到一名男生和一名女生的概率为12 = 3.
22.【答案】(1)证明:连接 ,
∵ 是∠ 的平分线,
∴ ∠ = 2∠ .
∵ ∠ = 2∠ ,
∴ ∠ = ∠ .
∴ / / .
∵ ∠ = 90°,
∴ ⊥ .
∵ / / ,
∴ ⊥ .
∵ 在⊙ 上,
∴ 是⊙ 的切线.
(2)解:∵ / / ,
∴ ∠ = ∠ .
∵ ∠ = ∠ ,
又∵ ∠ = ∠ ,
∴ ∠ = ∠ .
又∵ ∠ = ∠ ,
∴△ ∽△ .
∴ =
.
∴ 2 =
∵ = 5, = 10,
∴ = 20,则 = 15.
∴⊙ 的半径长 7.5.
(3)解:∵△ ∽△ ,
∴ =
= 1 2.
设 = , = 2 ,
∵ ∠ = 90°,
∴ 2 + 2 = 2,即 2 + 4 2 = 152.
∴ = 3 5.
∴ = 3 5.
∴ sin∠ = 5.5
∴ sin∠ = sin∠ = 5.5
23.【答案】解:(1)把 (4,0)、 (0,2)代入 = 2 + + 得:
16 + 4 + = 0
= 2 ,
解得: =
7
2,
= 2
∴ = 2 + 72 + 2;
(2) ∵ (4,0)、 (0,2),
设直线 的解析式为 = + ,把 、 坐标代入得:
0 = 4 +
2 = ,
= 1
解得: 2,
= 2
∴直线 的解析式为 = 12 + 2;
∵ ( , 0)(0 ≤ ≤ 4),
则 ( , 2 + 72 + 2), ( ,
1
2 + 2),
∴ = 1 2 72 + 2, = + 2 + 2,
当 为线段 的中点时,则有 2 = ,
1
即:2( 2 + 2) =
2 + 72 + 2,
解得 1 = 4(
1
三点重合,舍去)或 2 = 2,
∴ ( 1 , 72 4 );
(3) ∵ = 2, = 4,
∴ tan∠ = = 1 2,
由(2)可知: (0,2)、 ( , 2 + 72 + 2), ( ,
1
2 + 2),,
∵ ∠ = ∠ ,
∴以 、 、 为顶点的三角形与△ 相似,分两种情况讨论:
①当∠ 为直角时,则∠ = ∠ ,
∴ tan∠ = tan∠ 1,即: = 2,
∴ 2 = 4 2 2 + ( 2 + 7,即: 2 + 2 2)
2 = 4[ 2 + (2 + 1 2)22 ]
11 3
解得: 1 = 2 (舍去), 2 = 2;
②当∠ 为直角时,则∠ = ∠ ,
∴ tan∠ = tan∠ 1,即: = 2,
∴ = 12
7
,即: 2 + 2 + 2 +
1
2 2 =
1
2 ,
7
解得 1 = 2, 2 = 0(舍去),
7 3
综上所述, 的值是2或2.
数学试题
第 I 卷(选择题)
一、选择题(本大题共 10 小题,共 40 分。在每小题列出的选项中,选出符合题目的一项)
1. 1分数4的相反数是( )
A. 14 B.
1
4 C. 4 D. ±
1
2
2. 一个立体图形的三视图如图所示,则该立体图形是( )
A. 圆柱
B. 圆锥
C. 长方体
D. 三棱柱
3. 下列计算正确的是( )
A. 2 3 = 6 B. (3 )2 = 6 2 C. 6 ÷ 3 = 2 D. 3 2 2 = 2 2
4. 1在数轴上表示不等式 2 < 0的解集,正确的是 ( )
A. B.
C. D.
5. 下列函数中, 的值随 值的增大而减小的是 ( )
A. = 2 + 1 B. = 2 + 1 C. = 2 + 1 D. = 2 + 1
6. 如图, 是⊙ 的直径,点 、 在⊙ 上,∠ = 30°,则∠ 的大小为( )
A. 150°
B. 130°
C. 120°
D. 60°
7. 若关于 的二次函数 = 2 3 + 的图象与 轴有两个交点,
且 ≥ 3,则从满足条件的所有整数 中随机选取一个,恰好是负数的概率是( )
A. 1 B. 13 2 C.
2
3 D.
5
6
8. 如图,正方形 的边长为 5,点 在 边上, = 2,连接 ,将△ 沿 翻折
得△ ′ ,延长 ′交 于点 .则 ′ 的长度为( )
A. 2
B. 94
C. 157
D. 3 2 2
9. 已知二次函数 = 2 + + 和一次函数 = + ,
则这两个函数在同一个平面直角坐标系中的大致图象是( )
A. B.
C. D.
10. 如图,正方形 的面积为 3,点 在边 上,且 = 1,∠ 的平分线交 于点 ,
点 , 分别是 , 的中点,则下列结论正确的有( )
① = ② = 6 22
③ △ 的面积是 1 ④ △ ≌△ ⑤∠ = 30°
A. 2个 B. 3个 C. 4个 D. 5个
第 II 卷(非选择题)
二、填空题(本大题共 4 小题,共 20 分)
11. ( 9)2的平方根是 ,64的立方根是 ,则 + = ______ .
12. “新冠”疫情肆虐全球,打疫苗是最有效的防护措施,据统计数据预测,2021年国药
中生北京公司年新冠病毒灭活疫苗产能和科兴中维二期年新冠病毒灭活疫苗产能之和将超
1600000000剂,用科学记数法表示 1600000000为______ .
13. 如图, 为钝角△ 中 边的中点,经过 的直线 将△ 分成了周长相等的两
部分,已知 = 8,∠ = 120°,则 = ______ .
14. 如图, 、 是双曲线 = ( < 0)上两点,连接 、
,过点 作 ⊥ 轴于点 ,交线段 于点 ,若△
的面积是 1, = 2 ,则 = ______ .
三、解答题(本大题共 9 小题,共 90 分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题 8分)
2( 1) ≥ 3
(1)解不等式组: 3 +4 > 并在数轴上表示解集.5
2
(2)先化简,再求值:(1 + 1 ) ÷ 1,其中 = 2 + 1.
16. (本小题 8分)
为响应乡村振兴号召,在外地创业成功的大学毕业生小姣毅然返乡当起了新农人,创办了果
蔬生态种植基地.最近,为给基地蔬菜施肥,她准备购买甲、乙两种有机肥.已知甲种有机肥每
吨的价格比乙种有机肥每吨的价格多 100元,购买 2吨甲种有机肥和 1吨乙种有机肥共需
1700元.甲、乙两种有机肥每吨各多少元?
17. (本小题 8分)
图①、图②、图③均是 6 × 6的正方形网格,每个小正方形的边长均为 1,其顶点称为格点,
△ 的顶点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作
图痕迹.
(1)在图①中确定一点 ,使四边形 是平行四边形;
(2)在图②中,在边 上确定一点 ,使 ⊥ ;
(3)在图③中确定一点 ,使△ 与△ 关于 对称.
18. (本小题 8分)
细心观察如图,认真分析各式,然后解答问题.
22 = 1 + ( )2 = 2, =
1
1 ,2
23 = 1 + ( 2)2 = 3, 2 =
2,
2
24 = 1 + ( 3)2 = 4,
3
3 = ,2
……
(1) 10 = ______ ;
(2)用含 ( 是正整数)的等式表示上述面积变化规律: 2 = ______ , = ______ ;
(3)若一个三角形的面积是 5,则它是第个______ 三角形;
(4)求出 21 + 22 + 23 + 2 24 + … + 10的值.
19. (本小题 10分)
图 1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意
图如图 2,摄像头 的仰角、俯角均为 15°,摄像头高度 = 160 ,识别的最远水平距离
= 150 .
(1)身高 208 的小杜,头部高度为 26 ,他站在离摄像头水平距离 130 的点 处,请问
小杜最少需要下蹲多少厘米才能被识别?
(2)身高 120 的小若,头部高度为 15 ,踮起脚尖可以增高 3 ,但仍无法被识别,社区
及时将摄像头的仰角、俯角都调整为 20°(如图 3),此时小若能被识别吗?请计算说明.
(精确到 0.1 ,参考数据: 15° ≈ 0.26, 15° ≈ 0.97, 15° ≈ 0.27, 20° ≈ 0.34,
20° ≈ 0.94, 20° ≈ 0.36)
20. (本小题 10分)
如图, 是半圆 的直径, 是半圆 上的一点(不与 , 重合),连接 ,点 为弧 的中
点,过点 作 ⊥ ,交 的延长线于点 .
(1)求证: 是半圆 的切线;
(2)若 = 6, = 4 3,求阴影部分的面积.
21. (本小题 12分)
为贯彻落实党的二十大关于深化全民阅读活动的重要部署,教育部印发了《全国青少年学生
读书行动实施方案》,于是某中学开展了以“书香润校园,好书伴成长”为主题的系列读书
活动.学校为了解学生周末的阅读情况,采用随机抽样的方式获取了若干名学生的周末阅读时
间数据,整理后得到下列不完整的图表:
类别 类 类 类 类
阅读时长 (小时) 0 ≤ < 1 1 ≤ < 2 2 ≤ < 3 ≥ 3
频数 8 4
请根据图表中提供的信息解答下面的问题:
(1)此次调查共抽取了______ 名学生, = ______ , = ______ ;
(2)扇形统计图中, 类所对应的扇形的圆心角是______ 度;
(3)已知在 类的 4名学生中有两名男生和两名女生,若从中随机抽取两人参加阅读分享活动,
请用列表或画树状图的方法求出恰好抽到一名男生和一名女生的概率.
22. (本小题 12分)
如图,已知:以 △ 的边 为直径作△ 的外接圆⊙ ,∠ 的平分线 交 于 ,交
⊙ 于 ,过 作 / / 交 的延长线于 . = 5, = 10,
(1)求证: 是⊙ 切线;
(2)求⊙ 的半径长;
(3)求 sin∠ 的值.
23. (本小题 14分)
如图,二次函数 = 2 + + 经过点 (4,0)、 (0,2),点 是 轴正半轴上一个动点,过点
作垂直于 轴的直线分别交抛物线和直线 于点 和点 .设点 的横坐标为 .
(1)求二次函数的表达式;
(2)若 、 、 三个点中恰有一点是其它两点所连线段的中点(三点重合除外)时,求 的值.
(3)点 在线段 上时,若以 、 、 为顶点的三角形与△ 相似,求 的值.
答案和解析
1.【答案】
1 1
【解析】分数4的相反数是 4.故选: .
2.【答案】
【解析】根据主视图和左视图为矩形判断出是柱体,
根据俯视图是三边形可判断出这个几何体应该是三棱柱.故选: .
3.【答案】
【解析】解: 、 2 3 = 2+3 = 5,原式计算错误,故选项不符合题意;
B、(3 )2 = 9 2,原式计算错误,故选项不符合题意;
C、 6 ÷ 3 = 6 3 = 3,原式计算错误,故选项不符合题意;
D、3 2 2 = 2 2,计算正确,故选项符合题意.故选: .
4.【答案】
1
【解析】 2 < 0
解得: < 1,
在数轴上表示为: 故选 A.
5.【答案】
【解析】 . = 2 + 1中,当 < 0 时, 的值随 的值增大而减小,不符合题意;
B. = 2 + 1中,当 > 0 时, 的值随 的值增大而减小,不符合题意;
C. = 2 + 1 中, > 0, 的值随 的值增大而增大,不符合题意;
D. = 2 + 1 中, < 0, 的值随 的值增大而减少,符合题意;
故选 D.
6.【答案】
【解析】∵ 是⊙ 的直径,∠ = 30°,
∴ ∠ = 2∠ = 60°,
∴ ∠ = 180° 60° = 120°.故选: .
7.【答案】
【解析】根据题意,关于 的二次函数 = 2 3 + 的图象与 轴有两个交点,则关于 的方程
2 3 + = 0 有两个不相等的实数根,
故该一元二次方程的根的判别式 > 0,即 = ( 3)2 4 × 1 × > 0,
9
解得 < 4,
又∵ ≥ 3,
∴ 3 ≤ < 94,
∴满足条件的所有整数为 3、 2、 1、0、1、2共计 6个,其中负数有 3、 2、 1共计 3个,
∴ 3 1满足条件的所有整数 中随机选取一个,恰好是负数的概率是6 = 2.故选: .
8.【答案】
【解析】如图所示,连接 ,
∵正方形 的边长为 5,
∴ = = 5,∠ = ∠ = ∠ = 90°,
由折叠得, ′ = = = 5, ′ = = 2,∠ ′ = ∠ = 90°,
∴ ∠ = ∠ ′ = 90°, = = 3,
在 △ 和 △ ′ 中,
=
= ′
∴ △ ≌ △ ′ ( ),
∴ = ′ ,
设 ′ = = ,则 = = 5 , = ′ + ′ = + 2,
在 △ 中,由勾股定理得, 2 = 2 + 2(2 + )2 = 32 + (5 )2,
解得, = 157,
15
即 ′ 的长度是 7,
故选: .
9.【答案】
【解析】解: .图象中二次函数 > 0, < 0,一次函数 > 0, > 0,故 A 不符合题意.
B. 图象中二次函数 > 0, > 0,又对称轴在 轴右侧,则 2 > 0,得出 < 0,矛盾,故 B 不符
合题意.
C.图象中二次函数 < 0, > 0,一次函数 < 0, > 0,故 C 符合题意.
D. 图象中二次函数 < 0, < 0,又对称轴在 轴右侧,则 2 > 0,得出 > 0,矛盾,故 D 不符
合题意.故选: .
10.【答案】
【解析】如图:过点 作 ⊥ ,交 于 ,
∵正方形 的面积为 3,
∴ = = = = 3,
∵ = 1,
∴ = 3 1,tan∠ = =
1 = 3,3 3
∴ ∠ = 30°,
∴ ∠ = ∠ ∠ = 60°, = 2 = 2,
∵ 平分∠ ,
∴ ∠ = ∠ = 12∠ = 30°,故⑤正确;
在 △ 中, = 3 = 1,
∴ = = 3 1,
∴ = ,
∴△ 是等腰直角三角形,
∴ = 2 = 2 × ( 3 1) = 6 2,
∴ ≠ ,故①错误,
∵ , 分别是 , 的中点,
∴ 是△ 的中位线,
∴ = 1 = 6 2;故②正确;2 2
∵ 平分∠ , ⊥ ,∠ = 90°,
∴ = = 1,
∴△ = 1的面积 2 × 2 × 1 = 1,故③正确;
∵ = ,∠ = ∠ = 90°, = ,
∴△ ≌△ ( ),故④正确;故选: .
11.【答案】7或 1
【解析】∵ ( 9)2 = 9,
∴ =± 3,
∵ 64的立方根是 4,
∴ = 4,
∴ + = 3 + 4 = 7 或 + = 3+ 4 = 1,
故答案为:7或 1.
12.【答案】1.6 × 109
【解析】1600000000 = 1.6 × 109.故答案为:1.6 × 109.
13.【答案】4
【解析】如图,延长 到 ,使 = ,连接 .
∵ ∠ = 120°,
∴ ∠ = 180° ∠ = 60°,
∴△ 是等边三角形,
∴ = = = 8.
∵ 为钝角△ 中 边的中点,经过 的直线 将△ 分成了周长相等的两部分,
∴ = , + + = + ,
∴ + = ,
∴ + = ,即 = ,
∵ = ,
∴ 是△ 的中位线,
∴ = 12 = 4.故答案为:4.
14.【答案】 4
【解析】解:如图,过点 作 ⊥ 轴于 ,
∵ ⊥ 轴,
∴ / / ,
∴△ ∽△ ,
∴ = = ,
∵ = 2 ,
∴ =
2
3,
∴ =
2
= 3,
设 = 2 ,则 = 3 ,
∴ ( , 3 ) ( 3 , 2 , 2 ),
∴ = 2 ,
∵△ 的面积是 1,
∴ 1 2 ( 2 ) = 1,
∴ = 4,
故答案为: 4.
2( 1) ≥ 3①
15.【答案】解:(1)解不等式组 3 +4 ,
5 > ②
解不等式①得: ≥ 1,
解不等式②得: < 2,
∴不等式组的解集为: 1 ≤ < 2,
将解集表示在数轴上,如图.
(2) = +1 ÷ ( +1)( 1)原式
= +1 ( +1)( 1)
= 1 1,
当 = 2 + 1时,
1 2
原式= .2+1 1 = 2
16.【答案】解:设甲种有机肥每吨 元,乙种有机肥每吨 元,
= 100
依题意得: 2 + = 1700,
= 600
解得: = 500.
答:甲种有机肥每吨 600元,乙种有机肥每吨 500元.
17.【答案】解:(1)在图①中点 即为所求;
(2)在图②中点 ,即为所求;
(3)在图③中点 即为所求.
【解析】(1)根据平行四边形的性质结合网格,即可求解;
(2)取格点 连接 交 于点 ,则点 即为所求;
(3)作△ 的全等图形△ ,作 / / ,交 的垂线 于点 ,则点 即为所求.
本题考查作图 轴对称变换,平行四边形的判定和性质,学会利用数形结合的思想解决问题是解
题的关键.
18. 10 【答案】 202
【解析】解:(1) 210 = 1 + ( 9)2 = 10,
∴ 10 = 10,
故答案为: 10;
(2) 2 = 1 + ( + 1)2 = ,
( )2 + 1 = + 1,2
=
2 ( 是正整数);
故答案是: ; ;
2
(3) ∵ = 2 = 5,
∴ = 20,
故答案为:20;
(4) 2 2 21 + 2 + 3 + … + 210
= ( 1 )22 + (
2
2 )
2 + ( 32 )
2 + … + ( )22
= 14 (1 + 2 + 3 + … + 10)
= 554.
19.【答案】解:(1)过 作 的垂线分别交仰角、俯角线于点 , ,交水平线于点 ,
在 △ 中,tan∠ = ,
∴ = 15° ≈ 130 × 0.27 = 35.1( ),
∵ = ,∠ = ∠ ,∠ = ∠ = 90°,
∴△ ≌△ ( ),
∴ = = 35.1 ,
∴ = 160 + 35.1 = 195.1( ),
∴小杜最少需要下蹲 208 195.1 = 12.9厘米才能被识别;
(2)如图 2,过 作 的垂线分别交仰角、俯角线于 . .交水平线于 ,
在 △ 中,tan∠ = ,
∴ = 20° ≈ 150 × 0.36 = 54.0( ),
∵ = ,∠ = ∠ ,∠ = ∠ = 90°,
∴△ ≌△ ( ),
∴ = = 54.0 ,
∴ = 160 54.0 = 106.0( ),
∴小若踮起脚尖后头顶的高度为 120 + 3 = 123( ),
∴小若头顶超出点 的高度为:123 106.0 = 17.0( ) > 15 ,
∴踮起脚尖小若能被识别.
20.【答案】(1)证明:∵点 为弧 的中点,
∴ � = � ,
∴ ∠ = ∠ ,
∴ 12∠ =
1
2∠ ,
∵ = ,
∴ ∠ = ∠ = 12∠ ,
∵ ∠ = 12∠ ,
∴ ∠ = ∠ ,
∴ / / ,
∵ ⊥ 交 的延长线于点 ,
∴ ∠ = 90°,
∴ ∠ = 180° ∠ = 90°,
∵ 是⊙ 的半径,且 ⊥ ,
∴ 是半圆 的切线.
(2)解:连接 ,
∵ ∠ = 90°, = 6, = 4 3,
∴ cos∠ = =
6 3
,
4 3 = 2
∴ ∠ = 30°,
∴ ∠ = ∠ = 2∠ = 60°,
∴ ∠ = 180° ∠ ∠ = 60°,
∵ = = ,
∴△ 和△ 都是等边三角形,
∴ = = = = ,
∴四边形 是菱形,
∴ / / ,
∴ ∠ = ∠ = 60°,
∴ ∠ = 90° ∠ = 30°,
∵ = 12 =
1
2 × 4 3 = 2 3,
∴ = 30° = 2 3 × 33 = 2,
∴ = = = 6 2 = 4,
∴ 1 1 1 1△ = △ = 2 = 2 × 4 × 2 3 = 4 3, △ = 2 = 2 × 2 × 2 3 = 2 3,
∵ 阴影 = △ + △ =
60× ×42 8
扇形 , ,扇形 360 = 3
∴ 阴影 = 4 3 + 2 3
8 8
3 = 6 3 3,
∴ 8 阴影部分的面积是 6 3 3.
21.【答案】40 18 10 162
【解析】解:(1)此次调查共抽取的学生人数为:8 ÷ 20% = 40(名),
∴ = 40 × 25% = 10,
∴ = 40 8 10 4 = 18,
故答案为:40,18,10;
(2) 18扇形统计图中, 类所对应的扇形的圆心角是 360° × 40 = 162°,
故答案为:162;
(3)画树状图如下:
共有 12种等可能的结果,其中恰好抽到一名男生和一名女生的结果有 8种,
∴ 8 2恰好抽到一名男生和一名女生的概率为12 = 3.
22.【答案】(1)证明:连接 ,
∵ 是∠ 的平分线,
∴ ∠ = 2∠ .
∵ ∠ = 2∠ ,
∴ ∠ = ∠ .
∴ / / .
∵ ∠ = 90°,
∴ ⊥ .
∵ / / ,
∴ ⊥ .
∵ 在⊙ 上,
∴ 是⊙ 的切线.
(2)解:∵ / / ,
∴ ∠ = ∠ .
∵ ∠ = ∠ ,
又∵ ∠ = ∠ ,
∴ ∠ = ∠ .
又∵ ∠ = ∠ ,
∴△ ∽△ .
∴ =
.
∴ 2 =
∵ = 5, = 10,
∴ = 20,则 = 15.
∴⊙ 的半径长 7.5.
(3)解:∵△ ∽△ ,
∴ =
= 1 2.
设 = , = 2 ,
∵ ∠ = 90°,
∴ 2 + 2 = 2,即 2 + 4 2 = 152.
∴ = 3 5.
∴ = 3 5.
∴ sin∠ = 5.5
∴ sin∠ = sin∠ = 5.5
23.【答案】解:(1)把 (4,0)、 (0,2)代入 = 2 + + 得:
16 + 4 + = 0
= 2 ,
解得: =
7
2,
= 2
∴ = 2 + 72 + 2;
(2) ∵ (4,0)、 (0,2),
设直线 的解析式为 = + ,把 、 坐标代入得:
0 = 4 +
2 = ,
= 1
解得: 2,
= 2
∴直线 的解析式为 = 12 + 2;
∵ ( , 0)(0 ≤ ≤ 4),
则 ( , 2 + 72 + 2), ( ,
1
2 + 2),
∴ = 1 2 72 + 2, = + 2 + 2,
当 为线段 的中点时,则有 2 = ,
1
即:2( 2 + 2) =
2 + 72 + 2,
解得 1 = 4(
1
三点重合,舍去)或 2 = 2,
∴ ( 1 , 72 4 );
(3) ∵ = 2, = 4,
∴ tan∠ = = 1 2,
由(2)可知: (0,2)、 ( , 2 + 72 + 2), ( ,
1
2 + 2),,
∵ ∠ = ∠ ,
∴以 、 、 为顶点的三角形与△ 相似,分两种情况讨论:
①当∠ 为直角时,则∠ = ∠ ,
∴ tan∠ = tan∠ 1,即: = 2,
∴ 2 = 4 2 2 + ( 2 + 7,即: 2 + 2 2)
2 = 4[ 2 + (2 + 1 2)22 ]
11 3
解得: 1 = 2 (舍去), 2 = 2;
②当∠ 为直角时,则∠ = ∠ ,
∴ tan∠ = tan∠ 1,即: = 2,
∴ = 12
7
,即: 2 + 2 + 2 +
1
2 2 =
1
2 ,
7
解得 1 = 2, 2 = 0(舍去),
7 3
综上所述, 的值是2或2.
同课章节目录
