第十九章 一次函数复习课(第一课时)课件(共19张PPT)2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 第十九章 一次函数复习课(第一课时)课件(共19张PPT)2022-2023学年人教版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 42.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 12:20:43 | ||
图片预览


文档简介
(共19张PPT)
第十九章 一次函数复习课(第一课时)
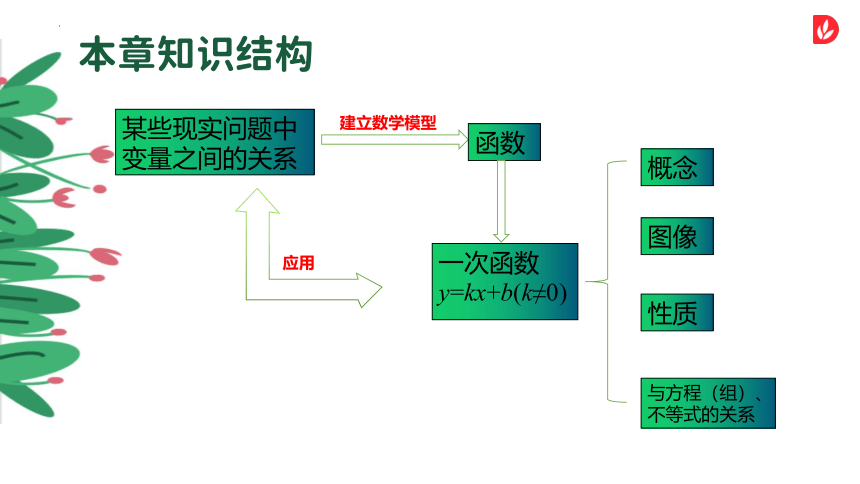
本章知识结构
某些现实问题中变量之间的关系
建立数学模型
函数
一次函数
y=kx+b(k≠0)
概念
性质
图像
与方程(组)、不等式的关系
应用
【复习回顾】
D
1
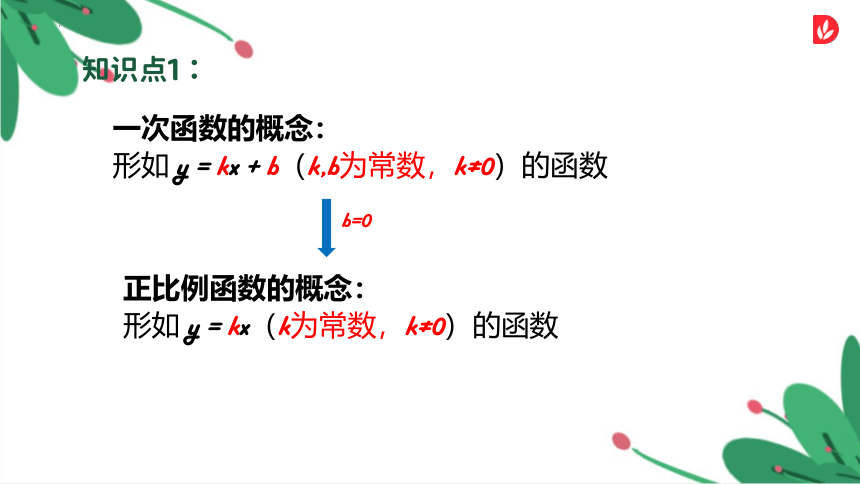
一次函数的概念:
形如 y = kx + b(k,b为常数,k≠0)的函数
b=0
正比例函数的概念:
形如 y = kx(k为常数,k≠0)的函数
知识点1:
【典例分析】
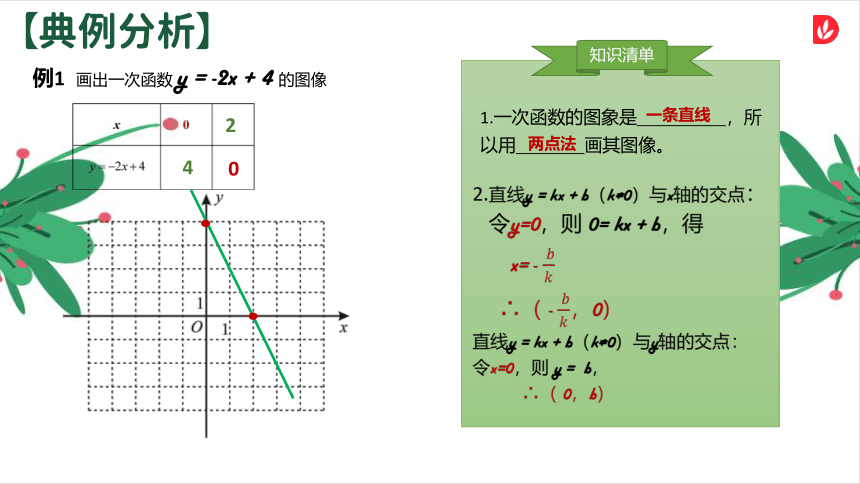
例1 画出一次函数 y = -2x + 4 的图像
知识清单
1.一次函数的图象是 ,所以用 画其图像。
一条直线
两点法
4
2
0
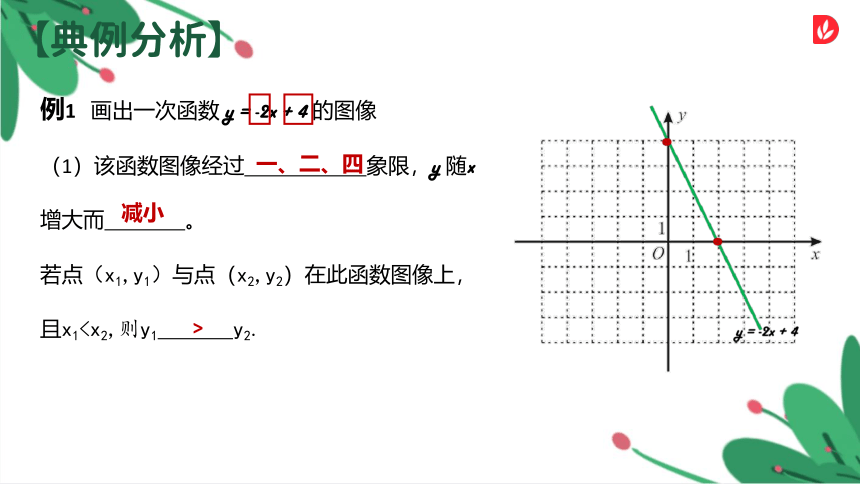
例1 画出一次函数 y = -2x + 4 的图像
(1)该函数图像经过 象限,y 随x增大而 。
若点(x1,y1)与点(x2,y2)在此函数图像上,且x1一、二、四
减小
>
【典例分析】
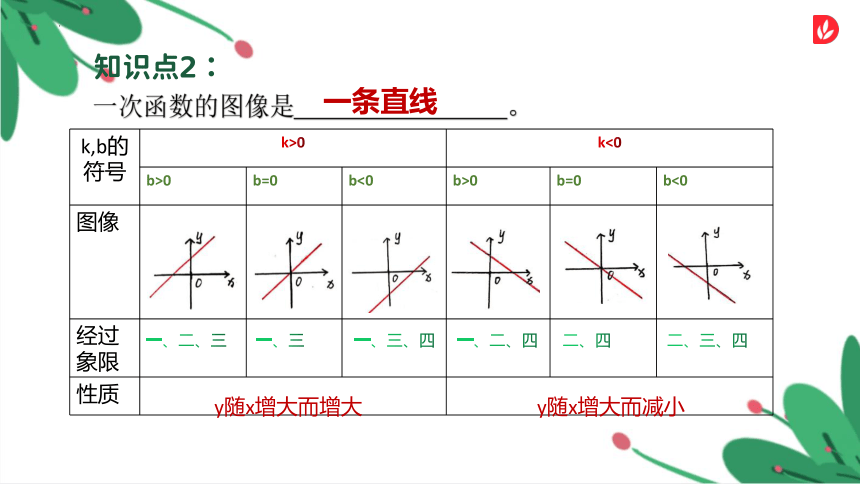
一次函数的图像是 。
k,b的符号 k>0 k>0 k>0 k<0 k<0 k<0
k<0 b>0 b=0 b<0 b>0 b=0 b<0
图像
经过象限
性质
一条直线
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y随x增大而增大
y随x增大而减小
知识点2:
(2)该函数图像与坐标轴围成的△AOB的面积是多少?AB长度是多少?
【典例分析】
(3)根据函数图像,方程-2x+4=0的解为 。方程-2x+4=4的解为 。
知识清单
x=0
x=2
用函数的观点看方程问题
求方程kx + b= 0的解
“ 数”
当一次函数y = kx + b的值y 为 时,求相应的 的值
“ 形”
求直线y = kx + b与 的交点的 坐标。
0
自变量x
x轴
横
【典例分析】
(4)根据函数图像,不等式-2x+4>0的解集为 。方程-2x+4<0的解集为 。
知识清单
x>2
x<2
用函数的观点看不等式问题
求不等式kx + b> 0(kx + b< 0)的解集
“ 数”
当一次函数y = kx + b 时,求相应的 的取值范围
“ 形”
求直线y = kx + b位于 的部分所对应的x的取值范围
y>0(或y<0)
自变量x
x轴上方(或下方)
【典例分析】
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如右图所示。
问题1 根据图象,你能得到哪些信息?
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如图所示。
问题2 你能求出他们运动时的函数解析式吗?
知识清单
1.待定系数法:
设、代、解、还原
解:设 y甲 = k1x ( k1≠0)
把点 (8,80) 代入,得:
80 =8× k1
解得 k1=10
∴y甲 = 10x
解:设 y 乙= k2x + b( k2≠0)
把点 (3,0) 与 (5,80) 分别代入,得:
0=3k2+ b ,
80=5k2 + b ,
{
{
解得
k2 = 40,
b = -120
∴y乙 = 40x-120
知识清单
一个待定系数,只需要一个点的坐标,列一个方程;
两个待定系数,需要两个点的坐标,列两个方程,组成方程组。
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如右图所示。
问题3 在乙出发几小时后追上甲?
y=10x ,
y=40x-120 ,
{
交点P代表乙追上甲
{
解得
x = 4,
y = 40
∴P(4,40)
∴4-3=1,即乙出发一小时后追上甲
用函数的观点看方程(组)问题
知识清单
二元一次方程
一次函数
解二元一次方程组
“数”
“形”
x为何值时,
两个函数的值相等
确定两条直线的交点坐标
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如右图所示。
问题4 什么时候甲在乙的前面? 什么时候乙在甲的前面?
04用函数的观点看不等式问题
【知识体系】
一次函数的概念:
形如 y = kx + b(k,b为常数,k≠0)的函数
b=0
正比例函数的概念:
形如 y = kx(k为常数,k≠0)的函数
一次函数与方程(组)、不等式的关系
标题
【当堂检测】
1.有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;函数 y随 x 的增大而增大的是________;函数 y 随 x 的增大而减小的是_____;图象在第一、二、三象限的是______.
②
③
①②③
④
x
y
2
=
2. 一次函数 y = -5x + 2 的图象不经过第______象限.
3. 点(-1,y1),(2,y2) 是直线 y = 2x + 1 上两点,则 y1____y2.
三
<
4.方程 x + 2 = 0 的解就是函数 y = x + 2 的图象与( )
A. x 轴交点的横坐标 B. y 轴交点的横坐标
C. y 轴交点的纵坐标 D. 以上都不对
5. 两个一次函数 y = -x + 5 和 y = -2x + 8 的图象的交点坐标是 ________.
A
(3,2)
【收获感悟】
1.你巩固了哪些知识?
2.本章主要蕴含了哪些数学思想?
【作业布置】
1.整理十九章的知识框架。
2.
第十九章 一次函数复习课(第一课时)
本章知识结构
某些现实问题中变量之间的关系
建立数学模型
函数
一次函数
y=kx+b(k≠0)
概念
性质
图像
与方程(组)、不等式的关系
应用
【复习回顾】
D
1
一次函数的概念:
形如 y = kx + b(k,b为常数,k≠0)的函数
b=0
正比例函数的概念:
形如 y = kx(k为常数,k≠0)的函数
知识点1:
【典例分析】
例1 画出一次函数 y = -2x + 4 的图像
知识清单
1.一次函数的图象是 ,所以用 画其图像。
一条直线
两点法
4
2
0
例1 画出一次函数 y = -2x + 4 的图像
(1)该函数图像经过 象限,y 随x增大而 。
若点(x1,y1)与点(x2,y2)在此函数图像上,且x1
减小
>
【典例分析】
一次函数的图像是 。
k,b的符号 k>0 k>0 k>0 k<0 k<0 k<0
k<0 b>0 b=0 b<0 b>0 b=0 b<0
图像
经过象限
性质
一条直线
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
y随x增大而增大
y随x增大而减小
知识点2:
(2)该函数图像与坐标轴围成的△AOB的面积是多少?AB长度是多少?
【典例分析】
(3)根据函数图像,方程-2x+4=0的解为 。方程-2x+4=4的解为 。
知识清单
x=0
x=2
用函数的观点看方程问题
求方程kx + b= 0的解
“ 数”
当一次函数y = kx + b的值y 为 时,求相应的 的值
“ 形”
求直线y = kx + b与 的交点的 坐标。
0
自变量x
x轴
横
【典例分析】
(4)根据函数图像,不等式-2x+4>0的解集为 。方程-2x+4<0的解集为 。
知识清单
x>2
x<2
用函数的观点看不等式问题
求不等式kx + b> 0(kx + b< 0)的解集
“ 数”
当一次函数y = kx + b 时,求相应的 的取值范围
“ 形”
求直线y = kx + b位于 的部分所对应的x的取值范围
y>0(或y<0)
自变量x
x轴上方(或下方)
【典例分析】
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如右图所示。
问题1 根据图象,你能得到哪些信息?
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如图所示。
问题2 你能求出他们运动时的函数解析式吗?
知识清单
1.待定系数法:
设、代、解、还原
解:设 y甲 = k1x ( k1≠0)
把点 (8,80) 代入,得:
80 =8× k1
解得 k1=10
∴y甲 = 10x
解:设 y 乙= k2x + b( k2≠0)
把点 (3,0) 与 (5,80) 分别代入,得:
0=3k2+ b ,
80=5k2 + b ,
{
{
解得
k2 = 40,
b = -120
∴y乙 = 40x-120
知识清单
一个待定系数,只需要一个点的坐标,列一个方程;
两个待定系数,需要两个点的坐标,列两个方程,组成方程组。
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如右图所示。
问题3 在乙出发几小时后追上甲?
y=10x ,
y=40x-120 ,
{
交点P代表乙追上甲
{
解得
x = 4,
y = 40
∴P(4,40)
∴4-3=1,即乙出发一小时后追上甲
用函数的观点看方程(组)问题
知识清单
二元一次方程
一次函数
解二元一次方程组
“数”
“形”
x为何值时,
两个函数的值相等
确定两条直线的交点坐标
【典例分析】
例2 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距千米的B地,他们行驶的路程y(千米)与所用时间x(小时)的函数关系如右图所示。
问题4 什么时候甲在乙的前面? 什么时候乙在甲的前面?
0
【知识体系】
一次函数的概念:
形如 y = kx + b(k,b为常数,k≠0)的函数
b=0
正比例函数的概念:
形如 y = kx(k为常数,k≠0)的函数
一次函数与方程(组)、不等式的关系
标题
【当堂检测】
1.有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;函数 y随 x 的增大而增大的是________;函数 y 随 x 的增大而减小的是_____;图象在第一、二、三象限的是______.
②
③
①②③
④
x
y
2
=
2. 一次函数 y = -5x + 2 的图象不经过第______象限.
3. 点(-1,y1),(2,y2) 是直线 y = 2x + 1 上两点,则 y1____y2.
三
<
4.方程 x + 2 = 0 的解就是函数 y = x + 2 的图象与( )
A. x 轴交点的横坐标 B. y 轴交点的横坐标
C. y 轴交点的纵坐标 D. 以上都不对
5. 两个一次函数 y = -x + 5 和 y = -2x + 8 的图象的交点坐标是 ________.
A
(3,2)
【收获感悟】
1.你巩固了哪些知识?
2.本章主要蕴含了哪些数学思想?
【作业布置】
1.整理十九章的知识框架。
2.
