九年级数学上册试题 1.2矩形的性质与判定习题 -北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 1.2矩形的性质与判定习题 -北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1021.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 15:56:34 | ||
图片预览


文档简介
1.2矩形的性质与判定习题
一、单选题
1.已知四边形ABCD的对角线相交于点O,且OA=OB=OC=OD,那么这个四边形是( )
A.是中心对称图形,但不是轴对称图形
B.是轴对称图形,但不是中心对称图形
C.既是中心对称图形,又是轴对称图形
D.既不是中心对称图形,又不是轴对称图形
2.已知矩形的两邻边长分别为3和4,给出结论:①该矩形的面积是6,②该矩形的对角线长是5.则这两个结论( ).
A.只有①是正确的 B.只有②是正确的
C.都是正确的 D.都是错误的
3.下列说法中正确的是( )
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直的四边形是矩形
D.有三个角是直角的四边形是矩形
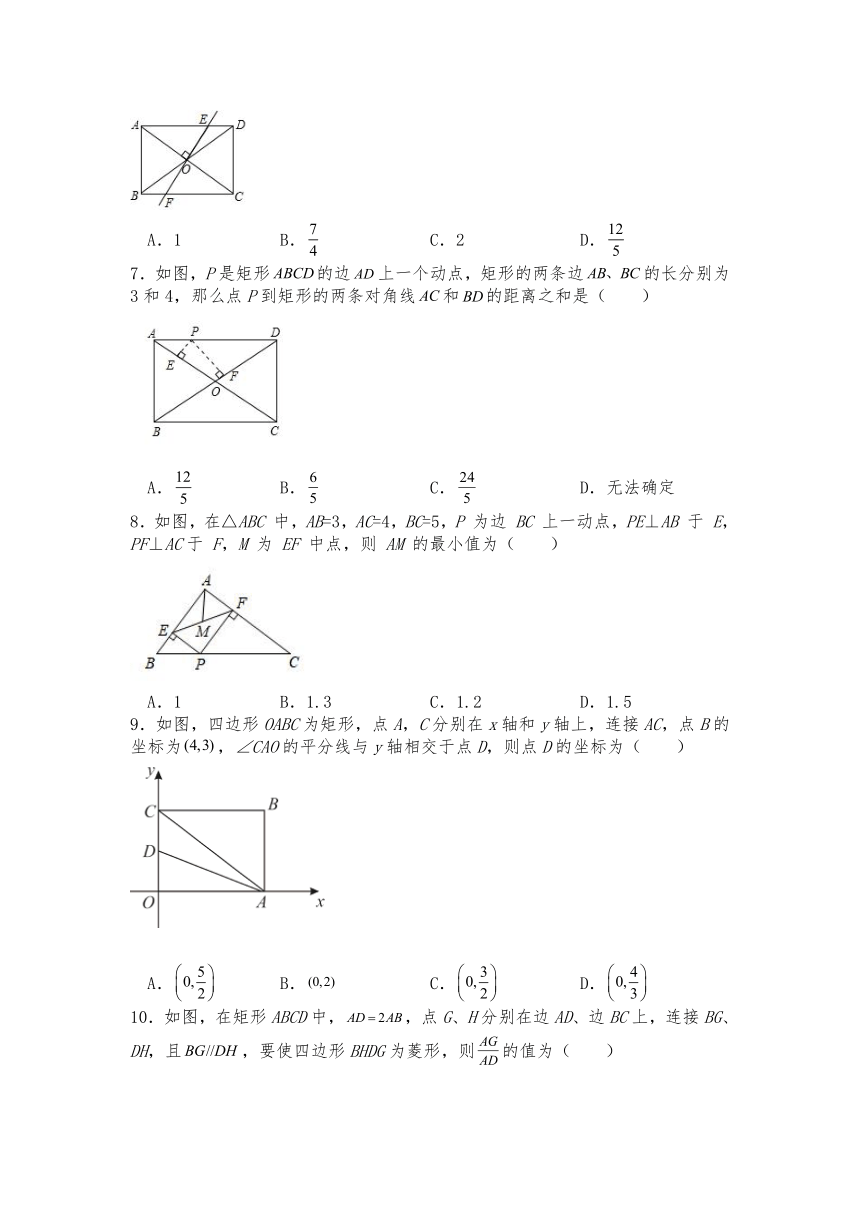
4.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
5.如图,在矩形中,点的坐标是,则的长是( )
A.3 B. C. D.4
6.如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是( )
A.1 B. C.2 D.
7.如图,P是矩形的边上一个动点,矩形的两条边的长分别为3和4,那么点P到矩形的两条对角线和的距离之和是( )
A. B. C. D.无法确定
8.如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
A.1 B.1.3 C.1.2 D.1.5
9.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为,∠CAO的平分线与y轴相交于点D,则点D的坐标为( )
A. B. C. D.
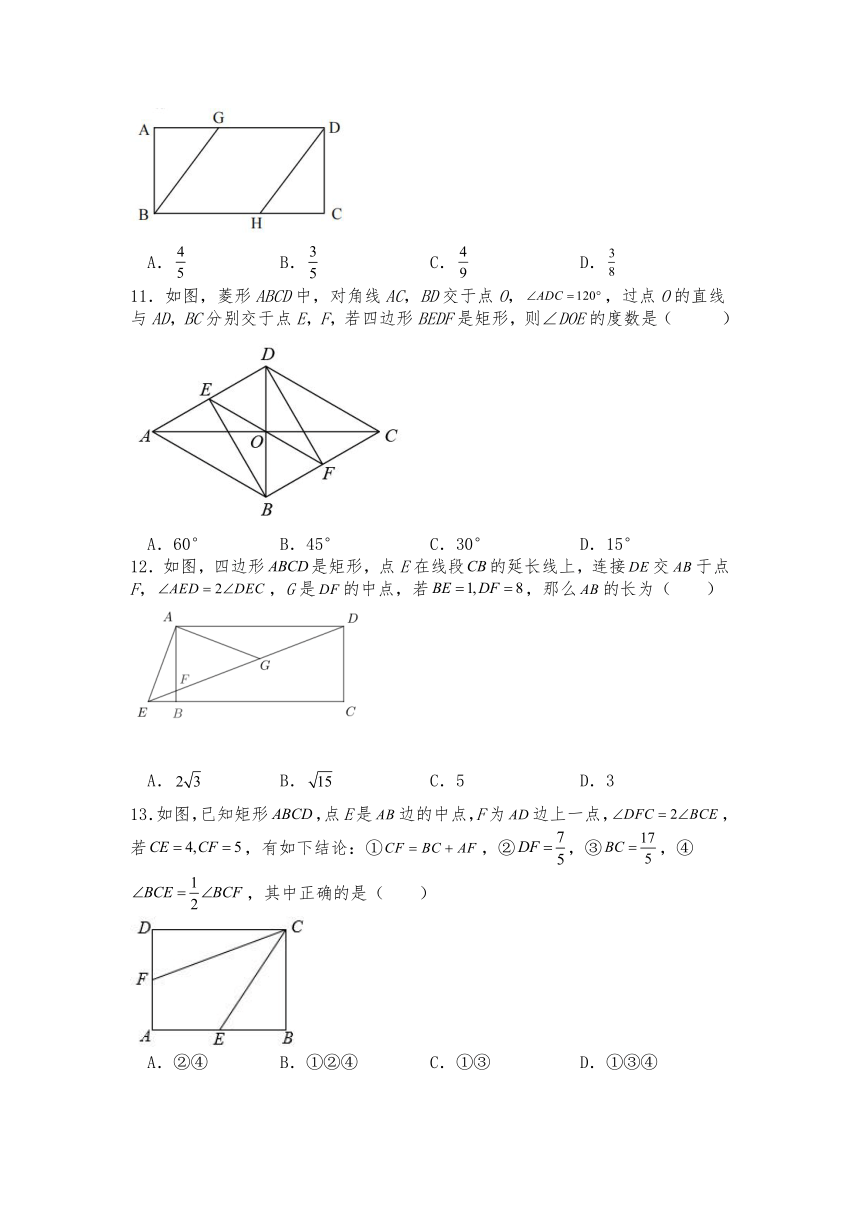
10.如图,在矩形ABCD中,,点G、H分别在边AD、边BC上,连接BG、DH,且,要使四边形BHDG为菱形,则的值为( )
A. B. C. D.
11.如图,菱形ABCD中,对角线AC,BD交于点O,,过点O的直线与AD,BC分别交于点E,F,若四边形BEDF是矩形,则∠DOE的度数是( )
A.60° B.45° C.30° D.15°
12.如图,四边形是矩形,点E在线段的延长线上,连接交于点F,,G是的中点,若,那么的长为( )
A. B. C.5 D.3
13.如图,已知矩形,点E是边的中点,F为边上一点,,若,有如下结论:①,②,③,④,其中正确的是( )
A.②④ B.①②④ C.①③ D.①③④
二、填空题
1.四边形中,交于O,给出条件①;②;③;④.其中能推得四边形是矩形的是(填序号)___________.
2.如图,延长矩形的边至点,使,若,则____.
3.如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果,,则EC的长_________.
4.如图,在矩形中,,交于点,、分别为、的中点.若,则的长为______.
5.如图,在矩形ABCD中,AB:AD=1:2,将点A沿折痕DE对折,使点A落在BC上的F点,则∠ADE=_____度.
6.如图,在长方形中,对角线、的交点为O,长方形的长、宽分别为、,过点O分别交、于E、F,那么图中阴影部分面积为________.
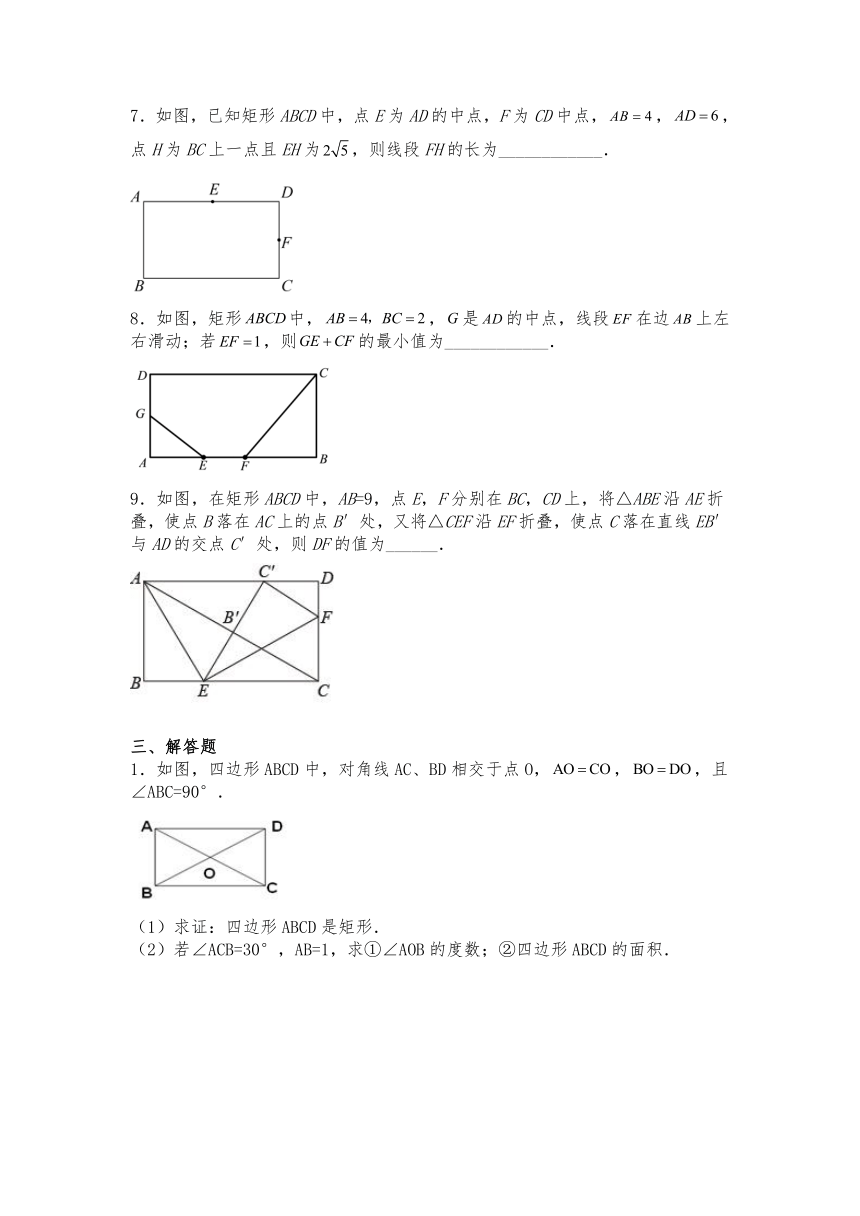
7.如图,已知矩形ABCD中,点E为AD的中点,F为CD中点,,,点H为BC上一点且EH为,则线段FH的长为____________.
8.如图,矩形中,,是的中点,线段在边上左右滑动;若,则的最小值为____________.
9.如图,在矩形ABCD中,AB=9,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,则DF的值为______.
三、解答题
1.如图,四边形ABCD中,对角线AC、BD相交于点O,,,且∠ABC=90°.
(1)求证:四边形ABCD是矩形.
(2)若∠ACB=30°,AB=1,求①∠AOB的度数;②四边形ABCD的面积.
2.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠DAB,CF=3,BF=4,求DF长.
3.如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.
(1)求证:BE=DE;
(2)试判断AB和PM,PN的数量关系并说明理由.
4.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,交DC的延长线于点E,BD=BE.
(1)求证:四边形ABCD是矩形.
(2)若∠AOB=60°,AB=4,求矩形ABCD的面积.
5.如图,四边形ABCD是矩形,点G为对角线AC的中点,E为AD边上一点,过点A作交CE延长线于点F,连接BF、FG.
(1)若,求证:AC垂直平分BF.
(2)若,求的度数;
6.在平行四边形中,,将沿翻折至,连接.求证:
(1);
(2)求证:;
(3)在平行四边形中,已知:,将沿翻折至,连接.若以为顶点的四边形是矩形,求的长.
7.已知矩形的对角线相交于点O,点E是边上一点,连接,且.
(1)如图1,求证:;
(2)如图2,设与相交于点F,与相交于点H,过点D作的平行线交的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(除外),使写出的每个三角形的面积都与的面积相等.
8.在矩形ABCD中,P是线段BC上的一个动点,将△ABP沿直线AP翻折,点B的对应点为E,直线PE与直线AD交于点F.
(1)如图①,当点F在AD的延长线上时,求证;
(2)若,BC足够长,当点E到直线AD的距离等于3时,求BP的长;
(3)若,.当点P、E、D在同一直线上(如图②)时,点P开始向点C运动,到与C重合时停止,则点F运动的路程是______.
答案
一、单选题
C.B.D.C.C.B.A.C.D.D.A.B.B.
二、填空题
1.③.
2.15°.
3.3cm.
4.2.
5.15°.
6.7.
7.或.
8.
9.3.
三、解答题
1.解:(1)证明:∵AO=CO,BO=DO
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵∠ABC=90°,∠ACB=300,AB=1
∴∠BAC=60°,AC=2,BC=
又∵矩形ABCD中,OA=OB
∴∠AOB=180°-2∠BAC=60°
S□ABCD=1×=
2.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.
3.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠CBD=∠EBD,
∴∠ADB=∠EBD,
∴BE=DE;
(2)解:PM+PN=AB;理由如下:
延长MP交BC于Q,如图所示:
∵AD∥BC,PM⊥AD,
∴PQ⊥BC,
∵∠CBD=∠EBD,PN⊥BE,
∴PQ=PN,
∴AB=MQ=PM+PQ=PM+PN.
4.(1)
∵四边形ABCD是平行四边形,
∴.
又∵点E在DC的延长线上,
∴,
又∵,
∴四边形ABEC是平行四边形,∴,
又∵BD=BE,
∴AC=BD
∴平行四边形ABCD是矩形;
(2)
∵在矩形ABCD中,∠AOB=60°,OA=OB.
∴△AOB是等边三角形,
∴∠BAC=60°
∴,
∴,
∴矩形ABCD的面积=.
5.(1)
证明:如图,连接BG,
∵AF⊥CE,
∴∠AFC=∠ABC=∠D=90°,
∵点G是AC的中点,
∴FG=BG=AG=GC=AC,
∴点G在BF的垂直平分线上,
在△AFE和△CDE中,
,
∴△AFE≌△CDE(ASA),
∴AF=DC=AB,
∴点A在BF的垂直平分线上,
∴AC垂直平分BF;
(2)
∵AC垂直平分BF;点G为对角线AC的中点,
∴FG=BG=AG=GC,
∴∠GCF=∠GFC,∠GBC=∠GCB,
∴∠FGB=∠AGF+∠AGB=2∠FCG+2∠BCG=2∠FCB=80°,
∵BG=FG,
∴.
∠BFG=50°
6.(1)
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠EAC=∠ACB,
∵△ABC≌△AB′C,
∴∠ACB=∠ACB′,BC=B′C,
∴∠EAC=∠ACB′,
∴AE=CE,
∴DE=B′E;
(2)
∵DE=B′E,
∴∠CB′D=∠B′DA=(180°-∠B′ED),
∵∠AEC=∠B′ED,
∴∠ACB′=∠CB′D,
∴B′D∥AC;
(3)
分两种情况:①如图1所示:
∵四边形ACDB′是矩形,
∴∠CAB′=90°,
∴∠BAC=90°,
∵∠B=60°,
∴AC=BC=2;
②如图2所示:
∵四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵BC=4,∠B=60°,
∴AC=4,
综上所述:AC的长为2或4.
7.(1)
证明:∵四边形是矩形,
∴与相等且互相平分,
∴,
∵,,
∴(SSS);
(2)
解:∵四边形ABCD是矩形,
∴AB=CD,∠BAE=∠CDE=90°,OA=OD=OB=OC,
又∵BE=CE,
∴Rt△ABE≌Rt△DCE(HL)
∴AE=DE,
∴,
∵OA=OD,AE=DE,
∴OE⊥AD,
∴,
∴,
∴,
∴;
∵,
∴∠OBF=∠OCH,,
又∵∠BOF=∠COH,OB=OC,
∴△BOF≌△COH(ASA),
∴,
∴,
∴,
∴,
∴;
∵,
∴∠AFE=∠DGE,∠EAF=∠EDG,
又∵AE=DE,
∴,
∴;
综上所述,、、、这4个三角形的面积与△AEF的面积相等.
8.(1)
∵四边形ABCD是矩形,
∴.
∴.
由翻折得:.
∴.
∴.
(2)
过点E作于F点, 则
∴.
当点E在矩形内部时,如图,
∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,
∴∠BAE=90° ∠EAF=60°.
由翻折得,,
∴,
∴由勾股定理得:,
解得.
当点E在矩形外部时,如图,
则∠BAE=∠BAD+∠EAF=120°.
由翻折得:,
∴∠APB=90° ∠BAP=30°,
∴,
则由勾股定理得
综上,线段BP的长为或.
(3)
如图,取BM=AB=6,AN=AB=6,连接MN,则四边形ABMN是正方形,
当点P由P、E、D重合时的状态运动到与M重合时,则F点的路程为线段DN=AD-AN=10-6=4,
当点P继续向点C运动直到与点C重合时,点F的路程为NF的长,即点F的路程为DN+NF,
由矩形性质得:AB=CD=6,∠D=90°,
由翻折的性质得:AB=AE=6,
当点P与点C重合时,由(1)知AF=CF.
则CF=AF=AD DF=10 DF,
在Rt△CDF中,由勾股定理得:,
解得:,
∴,
∴点F的运动路程为:DN+NF=4+0.8=4.8.
故答案为:4.8.
一、单选题
1.已知四边形ABCD的对角线相交于点O,且OA=OB=OC=OD,那么这个四边形是( )
A.是中心对称图形,但不是轴对称图形
B.是轴对称图形,但不是中心对称图形
C.既是中心对称图形,又是轴对称图形
D.既不是中心对称图形,又不是轴对称图形
2.已知矩形的两邻边长分别为3和4,给出结论:①该矩形的面积是6,②该矩形的对角线长是5.则这两个结论( ).
A.只有①是正确的 B.只有②是正确的
C.都是正确的 D.都是错误的
3.下列说法中正确的是( )
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直的四边形是矩形
D.有三个角是直角的四边形是矩形
4.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
5.如图,在矩形中,点的坐标是,则的长是( )
A.3 B. C. D.4
6.如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是( )
A.1 B. C.2 D.
7.如图,P是矩形的边上一个动点,矩形的两条边的长分别为3和4,那么点P到矩形的两条对角线和的距离之和是( )
A. B. C. D.无法确定
8.如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
A.1 B.1.3 C.1.2 D.1.5
9.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为,∠CAO的平分线与y轴相交于点D,则点D的坐标为( )
A. B. C. D.
10.如图,在矩形ABCD中,,点G、H分别在边AD、边BC上,连接BG、DH,且,要使四边形BHDG为菱形,则的值为( )
A. B. C. D.
11.如图,菱形ABCD中,对角线AC,BD交于点O,,过点O的直线与AD,BC分别交于点E,F,若四边形BEDF是矩形,则∠DOE的度数是( )
A.60° B.45° C.30° D.15°
12.如图,四边形是矩形,点E在线段的延长线上,连接交于点F,,G是的中点,若,那么的长为( )
A. B. C.5 D.3
13.如图,已知矩形,点E是边的中点,F为边上一点,,若,有如下结论:①,②,③,④,其中正确的是( )
A.②④ B.①②④ C.①③ D.①③④
二、填空题
1.四边形中,交于O,给出条件①;②;③;④.其中能推得四边形是矩形的是(填序号)___________.
2.如图,延长矩形的边至点,使,若,则____.
3.如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果,,则EC的长_________.
4.如图,在矩形中,,交于点,、分别为、的中点.若,则的长为______.
5.如图,在矩形ABCD中,AB:AD=1:2,将点A沿折痕DE对折,使点A落在BC上的F点,则∠ADE=_____度.
6.如图,在长方形中,对角线、的交点为O,长方形的长、宽分别为、,过点O分别交、于E、F,那么图中阴影部分面积为________.
7.如图,已知矩形ABCD中,点E为AD的中点,F为CD中点,,,点H为BC上一点且EH为,则线段FH的长为____________.
8.如图,矩形中,,是的中点,线段在边上左右滑动;若,则的最小值为____________.
9.如图,在矩形ABCD中,AB=9,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,则DF的值为______.
三、解答题
1.如图,四边形ABCD中,对角线AC、BD相交于点O,,,且∠ABC=90°.
(1)求证:四边形ABCD是矩形.
(2)若∠ACB=30°,AB=1,求①∠AOB的度数;②四边形ABCD的面积.
2.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠DAB,CF=3,BF=4,求DF长.
3.如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.
(1)求证:BE=DE;
(2)试判断AB和PM,PN的数量关系并说明理由.
4.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,交DC的延长线于点E,BD=BE.
(1)求证:四边形ABCD是矩形.
(2)若∠AOB=60°,AB=4,求矩形ABCD的面积.
5.如图,四边形ABCD是矩形,点G为对角线AC的中点,E为AD边上一点,过点A作交CE延长线于点F,连接BF、FG.
(1)若,求证:AC垂直平分BF.
(2)若,求的度数;
6.在平行四边形中,,将沿翻折至,连接.求证:
(1);
(2)求证:;
(3)在平行四边形中,已知:,将沿翻折至,连接.若以为顶点的四边形是矩形,求的长.
7.已知矩形的对角线相交于点O,点E是边上一点,连接,且.
(1)如图1,求证:;
(2)如图2,设与相交于点F,与相交于点H,过点D作的平行线交的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(除外),使写出的每个三角形的面积都与的面积相等.
8.在矩形ABCD中,P是线段BC上的一个动点,将△ABP沿直线AP翻折,点B的对应点为E,直线PE与直线AD交于点F.
(1)如图①,当点F在AD的延长线上时,求证;
(2)若,BC足够长,当点E到直线AD的距离等于3时,求BP的长;
(3)若,.当点P、E、D在同一直线上(如图②)时,点P开始向点C运动,到与C重合时停止,则点F运动的路程是______.
答案
一、单选题
C.B.D.C.C.B.A.C.D.D.A.B.B.
二、填空题
1.③.
2.15°.
3.3cm.
4.2.
5.15°.
6.7.
7.或.
8.
9.3.
三、解答题
1.解:(1)证明:∵AO=CO,BO=DO
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵∠ABC=90°,∠ACB=300,AB=1
∴∠BAC=60°,AC=2,BC=
又∵矩形ABCD中,OA=OB
∴∠AOB=180°-2∠BAC=60°
S□ABCD=1×=
2.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.
3.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠CBD=∠EBD,
∴∠ADB=∠EBD,
∴BE=DE;
(2)解:PM+PN=AB;理由如下:
延长MP交BC于Q,如图所示:
∵AD∥BC,PM⊥AD,
∴PQ⊥BC,
∵∠CBD=∠EBD,PN⊥BE,
∴PQ=PN,
∴AB=MQ=PM+PQ=PM+PN.
4.(1)
∵四边形ABCD是平行四边形,
∴.
又∵点E在DC的延长线上,
∴,
又∵,
∴四边形ABEC是平行四边形,∴,
又∵BD=BE,
∴AC=BD
∴平行四边形ABCD是矩形;
(2)
∵在矩形ABCD中,∠AOB=60°,OA=OB.
∴△AOB是等边三角形,
∴∠BAC=60°
∴,
∴,
∴矩形ABCD的面积=.
5.(1)
证明:如图,连接BG,
∵AF⊥CE,
∴∠AFC=∠ABC=∠D=90°,
∵点G是AC的中点,
∴FG=BG=AG=GC=AC,
∴点G在BF的垂直平分线上,
在△AFE和△CDE中,
,
∴△AFE≌△CDE(ASA),
∴AF=DC=AB,
∴点A在BF的垂直平分线上,
∴AC垂直平分BF;
(2)
∵AC垂直平分BF;点G为对角线AC的中点,
∴FG=BG=AG=GC,
∴∠GCF=∠GFC,∠GBC=∠GCB,
∴∠FGB=∠AGF+∠AGB=2∠FCG+2∠BCG=2∠FCB=80°,
∵BG=FG,
∴.
∠BFG=50°
6.(1)
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠EAC=∠ACB,
∵△ABC≌△AB′C,
∴∠ACB=∠ACB′,BC=B′C,
∴∠EAC=∠ACB′,
∴AE=CE,
∴DE=B′E;
(2)
∵DE=B′E,
∴∠CB′D=∠B′DA=(180°-∠B′ED),
∵∠AEC=∠B′ED,
∴∠ACB′=∠CB′D,
∴B′D∥AC;
(3)
分两种情况:①如图1所示:
∵四边形ACDB′是矩形,
∴∠CAB′=90°,
∴∠BAC=90°,
∵∠B=60°,
∴AC=BC=2;
②如图2所示:
∵四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵BC=4,∠B=60°,
∴AC=4,
综上所述:AC的长为2或4.
7.(1)
证明:∵四边形是矩形,
∴与相等且互相平分,
∴,
∵,,
∴(SSS);
(2)
解:∵四边形ABCD是矩形,
∴AB=CD,∠BAE=∠CDE=90°,OA=OD=OB=OC,
又∵BE=CE,
∴Rt△ABE≌Rt△DCE(HL)
∴AE=DE,
∴,
∵OA=OD,AE=DE,
∴OE⊥AD,
∴,
∴,
∴,
∴;
∵,
∴∠OBF=∠OCH,,
又∵∠BOF=∠COH,OB=OC,
∴△BOF≌△COH(ASA),
∴,
∴,
∴,
∴,
∴;
∵,
∴∠AFE=∠DGE,∠EAF=∠EDG,
又∵AE=DE,
∴,
∴;
综上所述,、、、这4个三角形的面积与△AEF的面积相等.
8.(1)
∵四边形ABCD是矩形,
∴.
∴.
由翻折得:.
∴.
∴.
(2)
过点E作于F点, 则
∴.
当点E在矩形内部时,如图,
∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,
∴∠BAE=90° ∠EAF=60°.
由翻折得,,
∴,
∴由勾股定理得:,
解得.
当点E在矩形外部时,如图,
则∠BAE=∠BAD+∠EAF=120°.
由翻折得:,
∴∠APB=90° ∠BAP=30°,
∴,
则由勾股定理得
综上,线段BP的长为或.
(3)
如图,取BM=AB=6,AN=AB=6,连接MN,则四边形ABMN是正方形,
当点P由P、E、D重合时的状态运动到与M重合时,则F点的路程为线段DN=AD-AN=10-6=4,
当点P继续向点C运动直到与点C重合时,点F的路程为NF的长,即点F的路程为DN+NF,
由矩形性质得:AB=CD=6,∠D=90°,
由翻折的性质得:AB=AE=6,
当点P与点C重合时,由(1)知AF=CF.
则CF=AF=AD DF=10 DF,
在Rt△CDF中,由勾股定理得:,
解得:,
∴,
∴点F的运动路程为:DN+NF=4+0.8=4.8.
故答案为:4.8.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
