九年级数学上册试题 6.2反比例函数的图像与性质习题-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 6.2反比例函数的图像与性质习题-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 276.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 16:00:38 | ||
图片预览



文档简介
6.2反比例函数的图像与性质习题
一、选择题
1.对于反比例函数y=﹣,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
2.下列说法正确的是( )
①反比例函数中自变量x的取值范围是x≠0﹔
②点P(3,-2)在反比例函数的图象上;
③反比例函数的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
3.对于反比例函数,下列说法正确的是( )
A.图象分布在第一、三象限内
B.图象经过点(1,2021)
C.当x>0时,y随x的增大而增大
D.若点A(x1、y1),B(x2,y2)都在该函数的图象上,且x1<x2,则y1>y2
4.如图,在平面直角坐标系中,是反比例函数图象上的一点,则的面积为( )
A. B. C. D.
5.如图,已知反比例函数的图像上有一点P,过点P作轴,垂足为点A,则的面积是( )
A.2 B.1 C. D.
6.已知点P(1,﹣3)在反比例函数(k≠0)的图象上,则k的值是( )
A.3 B.﹣3 C. D.
7.在平面直角坐标系中,点A、B、C分别在三个不同的象限,若反比例函数的图象经过其中两点,则的值为( )
A. B.6 C.或6 D.
8.函数的图象经过一组平移后,得到函数的图象,这组平移正确的是( )
A.先向上平移1个单位,再向左平移1个单位
B.先向右平移1个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移1个单位
D.先向下平移1个单位,再向右平移1个单位
9.在反比例函数图像上,到轴和轴的距离相等的点( )
A.1个 B.2个 C.4个 D.无数多个
10.反比例函数y=的图象如图所示,则k的值可能是( )
A.﹣1 B. C.3 D.4
二、填空题
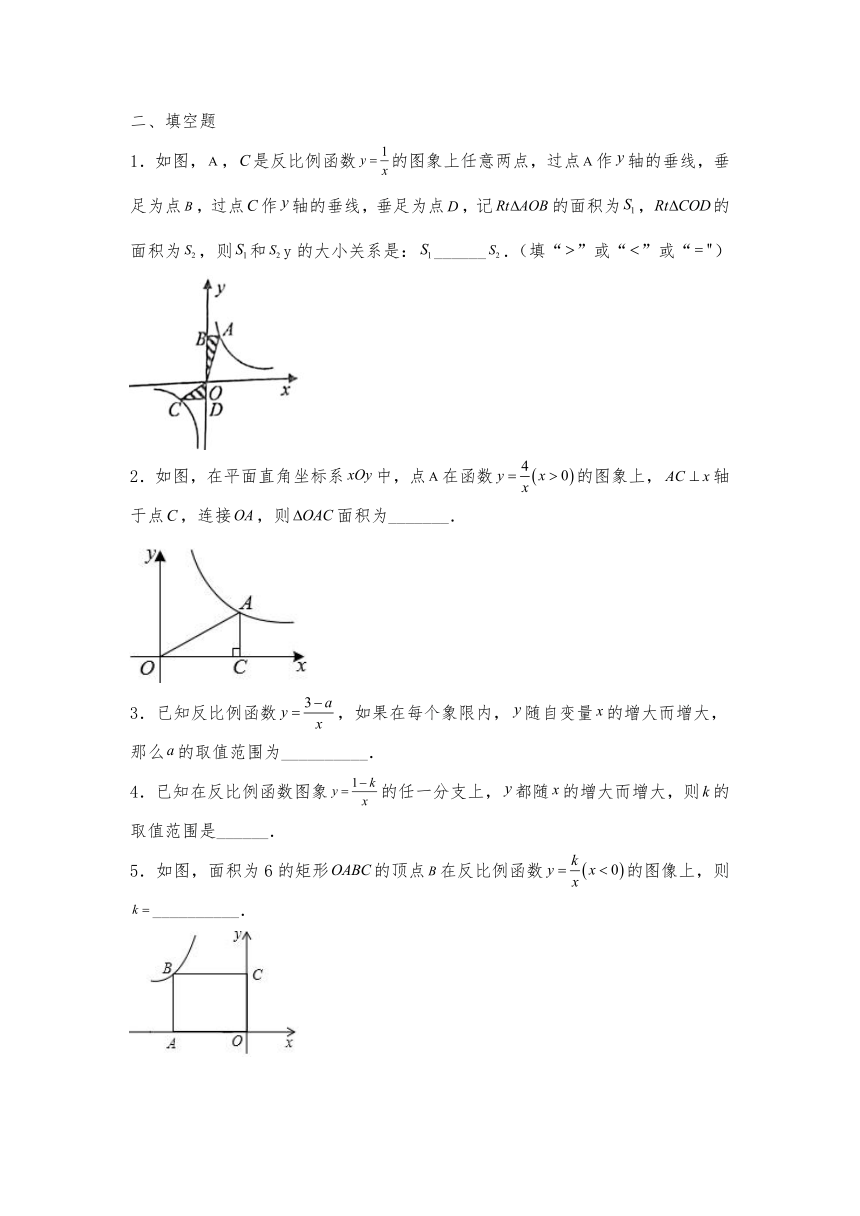
1.如图,,是反比例函数的图象上任意两点,过点作轴的垂线,垂足为点,过点作轴的垂线,垂足为点,记的面积为,的面积为,则和y的大小关系是:______.(填“”或“”或“")
2.如图,在平面直角坐标系中,点在函数的图象上,轴于点,连接,则面积为_______.
3.已知反比例函数,如果在每个象限内,随自变量的增大而增大,那么的取值范围为__________.
4.已知在反比例函数图象的任一分支上,都随的增大而增大,则的取值范围是______.
5.如图,面积为6的矩形的顶点在反比例函数的图像上,则__________.
6.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,则这个函数的表达式为________.
7.点(1,4)在反比例函数(k≠0)的图象上,则k=___.
8.如图,反比例函数的图象经过点A(-1,-2).则当x>1时,函数值y的取值范围是_________
9.已知反比例函数的图像经过点、,则k的值等于_____.
三、解答题
1.已知反比例函数.
(1)如果这个函数的图像经过点(2,-1),求k的值;
(2)如果在这个函数图像所在的每个象限内, y的值随x的值增大而减小,求k的取值范围.
2.在反比例函数的图像的每一条曲线上,都随的增大而减小.在曲线上取一点A,分别向轴、轴作垂线段,垂足分别为B、C,坐标原点为O,若四边形ABOC面积为6,求的值.
3.在反比例函数图象的每一条曲线上,y随x的增大而减小.
(1)函数经过哪些象限?
(2)求的取值范围
4.如图,在平面直角坐标系中.已知一次函数的图象与反比例函数的图象交于点和点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象,直接写出当不等式成立时,的取值范围.
5.已知反比例函数.
求:
(1)关于的函数解析式;
(2)当时函数的值.
6.已知反比例函数的图象经过点.
(1)求此函数的表达式;
(2)画出此函数在第一象限内的图象.
(3)根据函数图象写出此函数的一条性质.
答案
一、选择题
C.A.C.B.B.B.B.B.B.B.
二、填空题
1.=.
2.2.
3..
4..
5.-6.
6..
7.4.
8.0<y<2
9.6
三、解答题
1.
(1)把x=2,y=-1代入的左右两边解得;
(2)∵在这个函数图像所在的每个象限内, y的值随x的值增大而减小,
∴2k+1>0,
解得:.
2.∵y的值随x的增大而减小,∴k>0.
由于点A在双曲线上,则S=|k|=6,
而k>0,所以k=6.
3.解:(1)∵反比例函数的图象上,y随x的增大而减小
∴函数经过第一、三象限,
(2)∵函数经过第一、三象限,
∴5-﹥0,
即﹤5
【中小学教辅资源店 微信:mlxt2022】
4.解:(1)在反比例函数的图象上
.
,.
把、代入一次函数
得,从而得到,,
.
(2)由(1)得
∵
∴一次函数图像在反比例函数图像上方
∴.
5.解:(1)根据题意,得
,
解得,;
∴该反比例函数的解析式是;
(2)由(1)知,该反比例函数的解析式是,
∴当时,,即.
6.∵反比例函数的图象经过点.
∴,解得.
∴此函数的表达式为;
函数在第一象限内的图象如图:
函数在第一象限,随的增大而减小.
一、选择题
1.对于反比例函数y=﹣,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
2.下列说法正确的是( )
①反比例函数中自变量x的取值范围是x≠0﹔
②点P(3,-2)在反比例函数的图象上;
③反比例函数的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
3.对于反比例函数,下列说法正确的是( )
A.图象分布在第一、三象限内
B.图象经过点(1,2021)
C.当x>0时,y随x的增大而增大
D.若点A(x1、y1),B(x2,y2)都在该函数的图象上,且x1<x2,则y1>y2
4.如图,在平面直角坐标系中,是反比例函数图象上的一点,则的面积为( )
A. B. C. D.
5.如图,已知反比例函数的图像上有一点P,过点P作轴,垂足为点A,则的面积是( )
A.2 B.1 C. D.
6.已知点P(1,﹣3)在反比例函数(k≠0)的图象上,则k的值是( )
A.3 B.﹣3 C. D.
7.在平面直角坐标系中,点A、B、C分别在三个不同的象限,若反比例函数的图象经过其中两点,则的值为( )
A. B.6 C.或6 D.
8.函数的图象经过一组平移后,得到函数的图象,这组平移正确的是( )
A.先向上平移1个单位,再向左平移1个单位
B.先向右平移1个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移1个单位
D.先向下平移1个单位,再向右平移1个单位
9.在反比例函数图像上,到轴和轴的距离相等的点( )
A.1个 B.2个 C.4个 D.无数多个
10.反比例函数y=的图象如图所示,则k的值可能是( )
A.﹣1 B. C.3 D.4
二、填空题
1.如图,,是反比例函数的图象上任意两点,过点作轴的垂线,垂足为点,过点作轴的垂线,垂足为点,记的面积为,的面积为,则和y的大小关系是:______.(填“”或“”或“")
2.如图,在平面直角坐标系中,点在函数的图象上,轴于点,连接,则面积为_______.
3.已知反比例函数,如果在每个象限内,随自变量的增大而增大,那么的取值范围为__________.
4.已知在反比例函数图象的任一分支上,都随的增大而增大,则的取值范围是______.
5.如图,面积为6的矩形的顶点在反比例函数的图像上,则__________.
6.某校举行田径运动会,学校准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,则这个函数的表达式为________.
7.点(1,4)在反比例函数(k≠0)的图象上,则k=___.
8.如图,反比例函数的图象经过点A(-1,-2).则当x>1时,函数值y的取值范围是_________
9.已知反比例函数的图像经过点、,则k的值等于_____.
三、解答题
1.已知反比例函数.
(1)如果这个函数的图像经过点(2,-1),求k的值;
(2)如果在这个函数图像所在的每个象限内, y的值随x的值增大而减小,求k的取值范围.
2.在反比例函数的图像的每一条曲线上,都随的增大而减小.在曲线上取一点A,分别向轴、轴作垂线段,垂足分别为B、C,坐标原点为O,若四边形ABOC面积为6,求的值.
3.在反比例函数图象的每一条曲线上,y随x的增大而减小.
(1)函数经过哪些象限?
(2)求的取值范围
4.如图,在平面直角坐标系中.已知一次函数的图象与反比例函数的图象交于点和点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象,直接写出当不等式成立时,的取值范围.
5.已知反比例函数.
求:
(1)关于的函数解析式;
(2)当时函数的值.
6.已知反比例函数的图象经过点.
(1)求此函数的表达式;
(2)画出此函数在第一象限内的图象.
(3)根据函数图象写出此函数的一条性质.
答案
一、选择题
C.A.C.B.B.B.B.B.B.B.
二、填空题
1.=.
2.2.
3..
4..
5.-6.
6..
7.4.
8.0<y<2
9.6
三、解答题
1.
(1)把x=2,y=-1代入的左右两边解得;
(2)∵在这个函数图像所在的每个象限内, y的值随x的值增大而减小,
∴2k+1>0,
解得:.
2.∵y的值随x的增大而减小,∴k>0.
由于点A在双曲线上,则S=|k|=6,
而k>0,所以k=6.
3.解:(1)∵反比例函数的图象上,y随x的增大而减小
∴函数经过第一、三象限,
(2)∵函数经过第一、三象限,
∴5-﹥0,
即﹤5
【中小学教辅资源店 微信:mlxt2022】
4.解:(1)在反比例函数的图象上
.
,.
把、代入一次函数
得,从而得到,,
.
(2)由(1)得
∵
∴一次函数图像在反比例函数图像上方
∴.
5.解:(1)根据题意,得
,
解得,;
∴该反比例函数的解析式是;
(2)由(1)知,该反比例函数的解析式是,
∴当时,,即.
6.∵反比例函数的图象经过点.
∴,解得.
∴此函数的表达式为;
函数在第一象限内的图象如图:
函数在第一象限,随的增大而减小.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
