人教版数学九年级上册 22.3.1 实际问题与二次函数 学案(无答案)
文档属性
| 名称 | 人教版数学九年级上册 22.3.1 实际问题与二次函数 学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 17:10:47 | ||
图片预览

文档简介
《22.3.1 实际问题与二次函数》任务学习单
探索微课、自主探究
构建认知冲突
要求:打开平板中愤怒的小鸟,你可以玩两关游戏,同时在玩游戏的过程中仔细观察并思考以下问题:
在游戏中,你可以看到小鸟的运动轨迹是一条 ;
如果我们用 的知识来分析小鸟的运动轨迹,应该先 ;
要想解决这个问题,你可以选择以 作为原点建立平面直角坐标系;
除了以 作为原点建立平面直角坐标系,还有没有其他方案?
试着对比你所想到的所有方案,选择 作为原点建立平面直角坐标系最好。
(二)明确学习目标
要求:观看微课之前,请快速浏览本次学习的认知目标,打开平板中的洋葱数学进行学习,观看《22.3.1实际问题与二次函数——先建系再解题》,如果在看微课时遇到不懂的问题,你可以暂停或重看微课,直到充分理解微课中所讲的知识内容并在下面的[ ]中打勾。
(三)自学引导问题
要求:在观看微课时,动手做摘要和笔记很重要。
首先,请你完成下列引导问题,遇到做不出来的题目,可能是因为你忘记或没理解微课中的关键概念,这时你可以随时回看微课。然后,提炼出本节课的知识重点,记录在反思栏处,用于以后课后或考前的高效复习。
阶段一:桥洞问题——实际问题,先建系 ☆微课对应时间:00:00~01:45☆
如图,一座拱桥的桥洞呈抛物线形,当桥洞里的水面宽4米时,离拱顶2米,如果水位下降1米,水面会变得多宽?
思路:① →② →③
解决:要想求出解析式,首先应该
前提:我们必须确定两个问题:① ;②
阶段二:桥洞问题——选择合适的原点 ☆微课对应时间:01:45~03:19☆
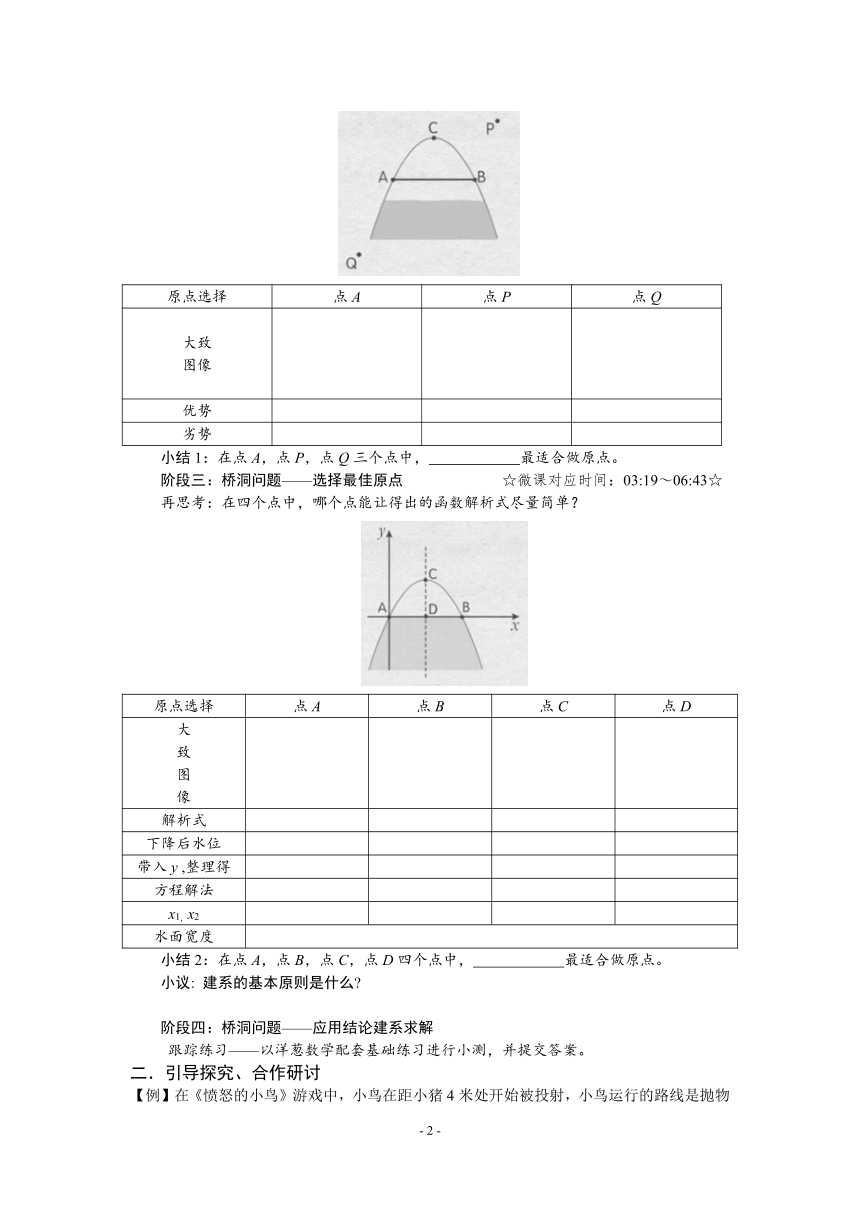
思考:在点A,点P,点Q三个点中,哪个点最适合做原点来建立平面直角坐标系?
原点选择 点A 点P 点Q
大致 图像
优势
劣势
小结1:在点A,点P,点Q三个点中, 最适合做原点。
阶段三:桥洞问题——选择最佳原点 ☆微课对应时间:03:19~06:43☆
再思考:在四个点中,哪个点能让得出的函数解析式尽量简单?
原点选择 点A 点B 点C 点D
大 致 图 像
解析式
下降后水位
带入y ,整理得
方程解法
x1,x2
水面宽度
小结2:在点A,点B,点C,点D四个点中, 最适合做原点。
小议: 建系的基本原则是什么
阶段四:桥洞问题——应用结论建系求解
跟踪练习——以洋葱数学配套基础练习进行小测,并提交答案。
引导探究、合作研讨
【例】在《愤怒的小鸟》游戏中,小鸟在距小猪4米处开始被投射,小鸟运行的路线是抛物线,当小鸟运行的水平距离为2.5米时,达到最大高度3.5米,然后小鸟准确射中小猪。已知小猪到地面的距离为3.05米。
提示:根据刚才动手玩游戏与微课学习,试着求解以下问题:
求抛物线的表达式
(2)若一小怪兽高为2.26米,起跳达到的最大高度为3.45米,此时小怪兽在小鸟正前方2米时竖直起跳,准备拦截小鸟的投射,从数学角度分析小怪兽能否成功?
(3)在(2)问的前提下,若小怪兽能够成功拦截小鸟的飞行,从数学角度来分析,小怪兽离小鸟的距离应该应该在什么范围之内?(结果保留根号)
在以上问题的基础上,能否试着设计一个该实际问题与二次函数相关的问题进行探究,并与同桌分享你的结论。
(提示:你可以分析函数的增减性、讨论某一区间的最值、计算面积、假设小鸟还可以反弹回来求最短路径,假设小怪兽在某点出发以一定的速度沿直线运动后于何处和小鸟相遇等)
综合应用、提高素养
1.(临沂中考·改编)在2018年俄罗斯世界杯小组赛中,C罗一颗漂亮的“电梯球”引起了世界轰动,若不考虑空气阻力与踢球的力度和角度,假设足球飞行的路线是一条抛物线,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴是直线t=;③足球被踢出9 s时落地;④足球被踢出1.5 s时,距离地面的高度是11 m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
2.(金华中考·改编)林丹和李宗伟是羽毛球比赛中的老对手,在2016年伦敦奥运会比赛中,甲(林丹)、乙(李宗伟)进行比赛,若羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1 m的P处发出一球,已知点O与球网的水平距离为5 m,球网的高度为1.55 m.
(1)建立合适的平面直角坐标系,并求出羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式;
(2)当时:
①求h的值;
②通过计算判断此球能否过网;
(3)若甲发球过网后,羽毛球飞行到离点O的水平距离为7 m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.
反思提高、体会思想
1.体会数形结合思想:我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休。”
从本质上来说:“数”与“形”反映了事物两个方面的属性,数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,
2.感悟数学建模思想:遇到实际问题,先转化为数学问题,选择最合适的原点建立平面直角坐标系,可以使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的。
探索微课、自主探究
构建认知冲突
要求:打开平板中愤怒的小鸟,你可以玩两关游戏,同时在玩游戏的过程中仔细观察并思考以下问题:
在游戏中,你可以看到小鸟的运动轨迹是一条 ;
如果我们用 的知识来分析小鸟的运动轨迹,应该先 ;
要想解决这个问题,你可以选择以 作为原点建立平面直角坐标系;
除了以 作为原点建立平面直角坐标系,还有没有其他方案?
试着对比你所想到的所有方案,选择 作为原点建立平面直角坐标系最好。
(二)明确学习目标
要求:观看微课之前,请快速浏览本次学习的认知目标,打开平板中的洋葱数学进行学习,观看《22.3.1实际问题与二次函数——先建系再解题》,如果在看微课时遇到不懂的问题,你可以暂停或重看微课,直到充分理解微课中所讲的知识内容并在下面的[ ]中打勾。
(三)自学引导问题
要求:在观看微课时,动手做摘要和笔记很重要。
首先,请你完成下列引导问题,遇到做不出来的题目,可能是因为你忘记或没理解微课中的关键概念,这时你可以随时回看微课。然后,提炼出本节课的知识重点,记录在反思栏处,用于以后课后或考前的高效复习。
阶段一:桥洞问题——实际问题,先建系 ☆微课对应时间:00:00~01:45☆
如图,一座拱桥的桥洞呈抛物线形,当桥洞里的水面宽4米时,离拱顶2米,如果水位下降1米,水面会变得多宽?
思路:① →② →③
解决:要想求出解析式,首先应该
前提:我们必须确定两个问题:① ;②
阶段二:桥洞问题——选择合适的原点 ☆微课对应时间:01:45~03:19☆
思考:在点A,点P,点Q三个点中,哪个点最适合做原点来建立平面直角坐标系?
原点选择 点A 点P 点Q
大致 图像
优势
劣势
小结1:在点A,点P,点Q三个点中, 最适合做原点。
阶段三:桥洞问题——选择最佳原点 ☆微课对应时间:03:19~06:43☆
再思考:在四个点中,哪个点能让得出的函数解析式尽量简单?
原点选择 点A 点B 点C 点D
大 致 图 像
解析式
下降后水位
带入y ,整理得
方程解法
x1,x2
水面宽度
小结2:在点A,点B,点C,点D四个点中, 最适合做原点。
小议: 建系的基本原则是什么
阶段四:桥洞问题——应用结论建系求解
跟踪练习——以洋葱数学配套基础练习进行小测,并提交答案。
引导探究、合作研讨
【例】在《愤怒的小鸟》游戏中,小鸟在距小猪4米处开始被投射,小鸟运行的路线是抛物线,当小鸟运行的水平距离为2.5米时,达到最大高度3.5米,然后小鸟准确射中小猪。已知小猪到地面的距离为3.05米。
提示:根据刚才动手玩游戏与微课学习,试着求解以下问题:
求抛物线的表达式
(2)若一小怪兽高为2.26米,起跳达到的最大高度为3.45米,此时小怪兽在小鸟正前方2米时竖直起跳,准备拦截小鸟的投射,从数学角度分析小怪兽能否成功?
(3)在(2)问的前提下,若小怪兽能够成功拦截小鸟的飞行,从数学角度来分析,小怪兽离小鸟的距离应该应该在什么范围之内?(结果保留根号)
在以上问题的基础上,能否试着设计一个该实际问题与二次函数相关的问题进行探究,并与同桌分享你的结论。
(提示:你可以分析函数的增减性、讨论某一区间的最值、计算面积、假设小鸟还可以反弹回来求最短路径,假设小怪兽在某点出发以一定的速度沿直线运动后于何处和小鸟相遇等)
综合应用、提高素养
1.(临沂中考·改编)在2018年俄罗斯世界杯小组赛中,C罗一颗漂亮的“电梯球”引起了世界轰动,若不考虑空气阻力与踢球的力度和角度,假设足球飞行的路线是一条抛物线,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴是直线t=;③足球被踢出9 s时落地;④足球被踢出1.5 s时,距离地面的高度是11 m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
2.(金华中考·改编)林丹和李宗伟是羽毛球比赛中的老对手,在2016年伦敦奥运会比赛中,甲(林丹)、乙(李宗伟)进行比赛,若羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1 m的P处发出一球,已知点O与球网的水平距离为5 m,球网的高度为1.55 m.
(1)建立合适的平面直角坐标系,并求出羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式;
(2)当时:
①求h的值;
②通过计算判断此球能否过网;
(3)若甲发球过网后,羽毛球飞行到离点O的水平距离为7 m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.
反思提高、体会思想
1.体会数形结合思想:我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休。”
从本质上来说:“数”与“形”反映了事物两个方面的属性,数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,
2.感悟数学建模思想:遇到实际问题,先转化为数学问题,选择最合适的原点建立平面直角坐标系,可以使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的。
同课章节目录
