离散型随机变量的数学期望(课件)苏教版[下学期]
文档属性
| 名称 | 离散型随机变量的数学期望(课件)苏教版[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 311.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-17 00:00:00 | ||
图片预览





文档简介
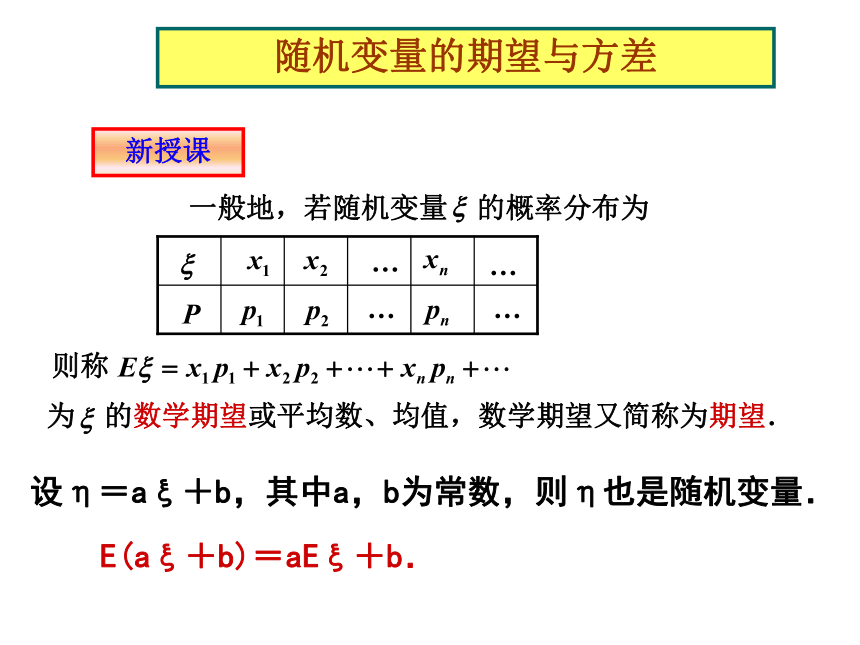
课件14张PPT。随机变量的期望与方差随机变量的期望与方差随机变量的期望与方差随机变量的期望与方差随机变量的期望与方差随机变量的期望与方差随机变量的期望与方差随机变量的期望与方差问题引入某射手射击所得环数 的分布列如下: 能否根据分布列估计射手n 次射击的平均环数? n 次射击的总环数约等于n 次射击的平均环数约等于随机变量的期望与方差新授课设η=aξ+b,其中a,b为常数,则η也是随机变量. E(aξ+b)=aEξ+b.
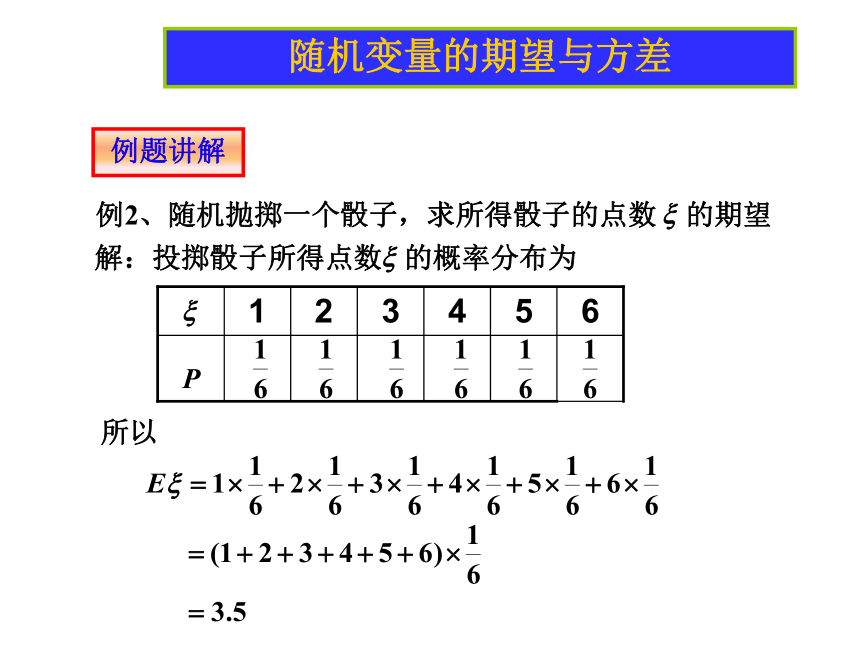
随机变量的期望与方差例题讲解 例1、篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,求他罚球一次的得分 的期望解:因为 , ,所以随机变量的期望与方差例题讲解例2、随机抛掷一个骰子,求所得骰子的点数 的期望所以随机变量的期望与方差例题讲解 例3、有一批数量很大的产品,其次品率是15%.对这批产品进行抽查,每次抽出1件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但每次抽查次数最多不超过10次.求抽查次数 的期望(结果保留三个有效数字). 解:抽查次数 取1~10的整数,从这批数量很大的产品中每次抽取一件检查的试验可以认为是彼此独立的,取次品的概率是0.15,取正品的概率是0.85,前k-1次取出正品而第k 次(k=1,2…9)取出次品的概率需要抽查10 次即前9次取出的都是正品的概率是随机变量的期望与方差例题讲解可得 的期望随机变量的期望与方差例4、高二(1)班的联欢会上设计了一项游戏,在一个
中袋中装有10个红球,20个白球,这些球除了颜色外
完全相同,某同学一次从中摸出5个球,其中红球的个
数为X,求X的数学期望。例5、从批量较大的成品中随机取出10件产品进行质量
检查,若这批产品的不合格率为0.05.设随机变量X表
示这10件产品中的不合格数,求随机变量X的数学期
望E(X)随机变量的期望与方差例题讲解例6、证明:服从二项分布 的随机变量的期望证明:(1) 0--1 分布 7、8、9、
随机变量的期望与方差例题讲解 例1、篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,求他罚球一次的得分 的期望解:因为 , ,所以随机变量的期望与方差例题讲解例2、随机抛掷一个骰子,求所得骰子的点数 的期望所以随机变量的期望与方差例题讲解 例3、有一批数量很大的产品,其次品率是15%.对这批产品进行抽查,每次抽出1件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但每次抽查次数最多不超过10次.求抽查次数 的期望(结果保留三个有效数字). 解:抽查次数 取1~10的整数,从这批数量很大的产品中每次抽取一件检查的试验可以认为是彼此独立的,取次品的概率是0.15,取正品的概率是0.85,前k-1次取出正品而第k 次(k=1,2…9)取出次品的概率需要抽查10 次即前9次取出的都是正品的概率是随机变量的期望与方差例题讲解可得 的期望随机变量的期望与方差例4、高二(1)班的联欢会上设计了一项游戏,在一个
中袋中装有10个红球,20个白球,这些球除了颜色外
完全相同,某同学一次从中摸出5个球,其中红球的个
数为X,求X的数学期望。例5、从批量较大的成品中随机取出10件产品进行质量
检查,若这批产品的不合格率为0.05.设随机变量X表
示这10件产品中的不合格数,求随机变量X的数学期
望E(X)随机变量的期望与方差例题讲解例6、证明:服从二项分布 的随机变量的期望证明:(1) 0--1 分布 7、8、9、
