浙江省吴兴高级中学2022-2023学年下学期高一年级6月教学质量检测数学试题(PDF版含解析)
文档属性
| 名称 | 浙江省吴兴高级中学2022-2023学年下学期高一年级6月教学质量检测数学试题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 754.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 14:43:18 | ||
图片预览




文档简介
吴兴高级中学 2022-2023学年下学期高一年级 6月教学质量检测
数学试卷
一、单选题(本大题共 8小题,共 40分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合 ,集合 ,则 ( )
A. B. C. D.
2. 若 是虚数单位 ,则 ( )
A. B. C. D.
3. 羽毛球运动是一项全民喜爱的体育运动,标准的羽毛球由 根羽毛固定在球托上,测得
每根羽毛在球托之外的长为 ,球托之外由羽毛围成的部分可看成一个圆台的侧面,测得
顶端所围成圆的直径是 ,底部所围成圆的直径是 ,据此可估算得球托之外羽毛所在
的曲面的展开图的圆心角为( )
A. B. C. D.
4. 设 是两条不同的直线, 是两个不同的平面,且直线 ,直线 ,则“ ”是
“ ”的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
5. 据你估计,一种商品在销售收入不变的条件下,其销量 与价格 之间的关系最可能是下
图中的( )
A. B.
C. D.
6. 现只有一把长为 的尺子,为了求得某小区草坪坛边缘 , 两点的距离 大于 ,
在草坪坛边缘找到点 与 ,已知 ,且 ,测得 ,
, ,则 ( )
A. B. C.
D.
7. 已知函数 , 为自然对数的底数 ,则 ( )
A. ,
B. ,当 时,
C. ,
D.
,当 时,
8. 已知把函数 的图象向左平移 后得到的图象关于 对称, 在
上具有单调性,则 的最大值为 ( )
A. B. C. D.
二、多选题(本大题共 4小题,共 20分。在每小题有多项符合题目要求)
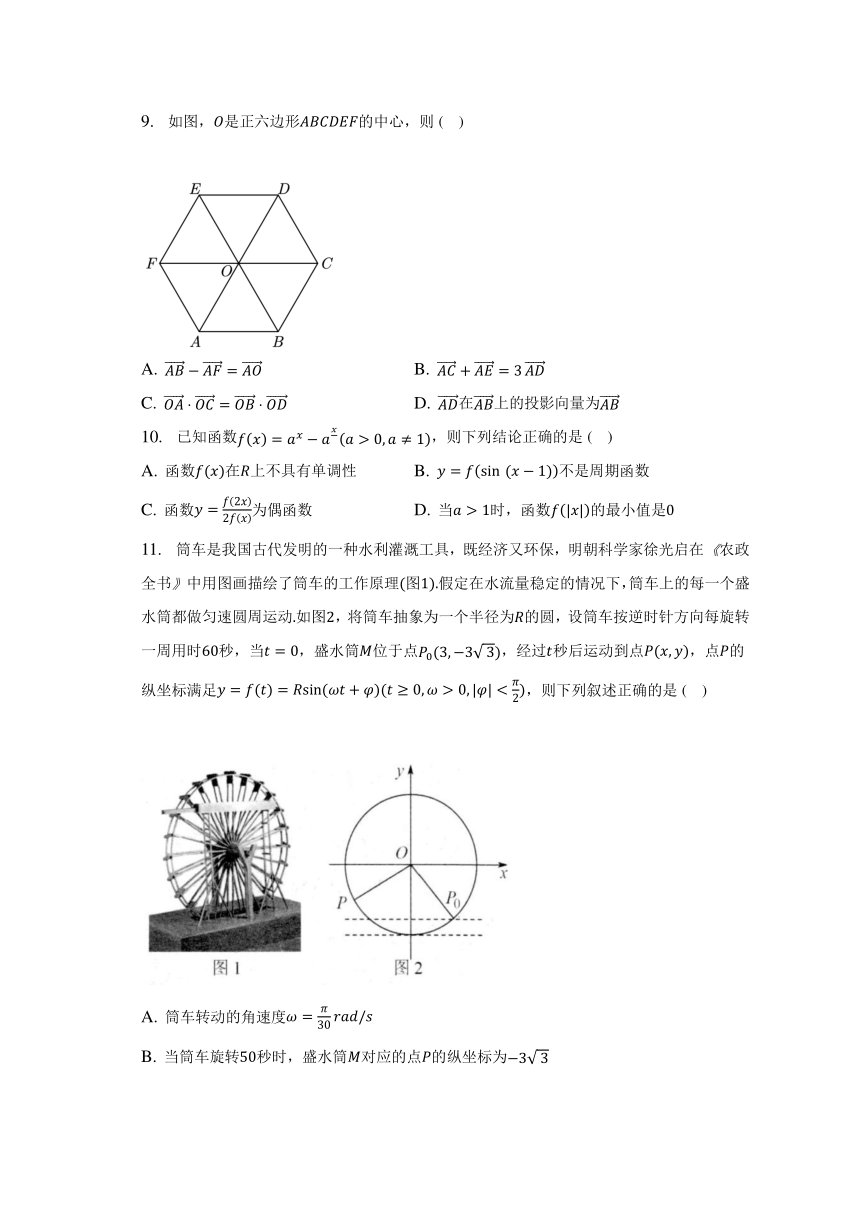
9. 如图, 是正六边形 的中心,则 ( )
A. B.
C. D. 在 上的投影向量为
10. 已知函数 ,则下列结论正确的是 ( )
A. 函数 在 上不具有单调性 B. 不是周期函数
C. 函数 为偶函数 D. 当 时,函数 的最小值是
11. 筒车是我国古代发明的一种水利灌溉工具,既经济又环保,明朝科学家徐光启在《农政
全书》中用图画描绘了筒车的工作原理 图 假定在水流量稳定的情况下,筒车上的每一个盛
水筒都做匀速圆周运动 如图 ,将筒车抽象为一个半径为 的圆,设筒车按逆时针方向每旋转
一周用时 秒,当 ,盛水筒 位于点 ,经过 秒后运动到点 ,点 的
纵坐标满足 ,则下列叙述正确的是 ( )
A. 筒车转动的角速度
B. 当筒车旋转 秒时,盛水筒 对应的点 的纵坐标为
C. 当筒车旋转 秒时,盛水筒 和初始点 的水平距离为
D. 盛水筒 第一次到达最高点需要的时间是 秒
12. 圆锥内半径最大的球称为该圆锥的内切球 若圆锥的顶点和底面的圆周都在同一个球面
上,则称该球为圆锥的外接球 如图,圆锥 的内切球和外接球的球心重合,且圆锥 的底
面直径为 ,则( )
A. 设内切球的半径为 ,外接球的半径为 ,则
B. 设内切球的表面积 ,外接球的表面积为 ,则
C. 设圆锥的体积为 ,内切球的体积为 ,则
D. 设 , 是圆锥底面圆上的两点,且 ,则平面 截内切球所得截面的面积为
三、填空题(本大题共 4小题,共 20分)
13. 已知函数 ,若 ,则 .
14. 将曲线 上所有点向左平移 个单位,得到函数 的图象,则 的
最小值为 .
15. 已知正三棱柱 的各条棱长都是 ,则直线 与平面 所成角的正切
值为 直线 与直线 所成角的余弦值为 .
16. 若函数 满足对任意 ,都有 成立,则称函数 在区
间 上是“被 约束的”,若函数 在区间 上是“被
约束的”,则实数 的取值范围是 .
四、解答题(本大题共 6小题,共 70分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题 分 在平面直角坐标系中,已知角 的顶点与原点 重合,始边与 轴的非负半
轴重合,它的终边过点
求 的值.
若角 满足 ,求 的值.
18. 本小题 分 某校数学兴趣小组,在过去一年一直在研究学校附近池塘里某种水生植物
的面积变化情况,自 年元且开始测量该水生植物的面积,此后每隔一个月 每月月底 测
量一次,通过一年的观察发现,自 年元旦起,该水生植物在池塘里面积增加的速度是越
来越快的.最初测得该水生植物面积为 ,二月底测得该水生植物的面积为 ,三月底
测得该水生植物的面积为 ,该水生植物的面积 单位: 与时间 单位:月 的关系有
两个函数模型可供选择,一个是同学甲提出的 ;另一个是同学乙提出
的 ,记 年元旦最初测量时间 的值为 .
根据本学期所学,请你判断哪个同学提出的函数模型更适合?并求出该函数模型的解析式;
池塘中该水生植物面积应该在几月份起是元旦开始研究时该水生植物面积的 倍以上?
参考数据: ,
19. 本小题 分 已知 , , 是平面上不同的三点,点 是此平面上任意一点,则“ , , 三
点共线”的充要条件是“存在实数 ,使得 ” 此结论往往称为向量的爪
子模型.
给出这个结论的证明
在 的边 、 上分别取点 、 ,使 , ,连结 、 交于点
设 , 利用上述结论,求出用 、 表示向量 的表达式.
20. 本小题 分 如图,在四边形 中, , , ,连接
, .
求 的值;
若 , ,求 面积的最大值.
21. 本小题 分 正三棱锥 的侧面是底边长为 ,顶角为 的等腰三角形.过点
作这个三棱锥的截面 ,点 、 分别在棱 、 上.
如图,作出平面 与平面 的交线;
周长的最小值是否存在?若存在,求出其最小值,并指出此时直线 与平面 的
位置关系;若不存在,请说明理由.
22. 本小题 分 已知函数 , .
直接写出 的解集
若 ,其中 ,求 的取值范围;
己知 为正.整.数.,求
的最小值 用 表示 .
答案和解析
1. 【解析】由题设 , 或 ,
所以 .故选: .
2.
【解析】由 ,则 ,故选 C.
3. 【解析】由题意知:
上 上
,解得 .
下 下
4. 【解析】 , 是两条不同的直线, , 是两个不同的平面,且 , ,
由“ ”不可推出“ ”,即充分性不成立;
由“ ”不可推出“ ”,即必要性不成立;
故“ ”是“ ”既不充分又不必要条件,故选 D.
5. 【解析】 销售收入不变, 定值 , .故选 C.
6. 【解析】因为 , , ,所以 .
因为 ,所以 ,
所以
7. 【解析】由题意分别作出 , 图象如下图,
经过第一、二、三象限, 经过第一、二象限.
又 , 由指数函数增长速度可知 与 在第一象限必有 个交点.
,当 时, 一定成立.故选 D.
8. 【解析】设函数 的图象向左平移 后得到函数 ,
,
则 图象关于 对称,
所以 ,
即 ,
可得: ,
,
当 时,可得: ,
,
, ,
令 ,则 , ,
由正弦函数的性质可知, 在 上具有单调性,
此时该单调区间的区间长度为: .
在区间 具有单调性,
其区间长度必定不能超过 .
可得: ,
,
, ,
的最大值为 ,故选 B.
9. 【解析】对于 , ,则 错;
对于 ,
,
显然 B错误;
正六边形
,
则 ,
,故 C正确;
由 为正六边形,连接 ,可得 .
故 在 上的投影向量为 .
则 D正确.故选 CD.
10. 【解析】当 时, 在 上为增函数,当 时, 在 上减函数,A错误;
对于 , 定义域是 , ,因此 是函数的一个
周期,B错误;
对于 ,由 得 ,函数定义域是 ,关于原点对称,
,
, ,所以函数为偶函数, C正确;
对于 ,当 时,
在 上为减函数,在 上为增函数,
当 时, 取得最小值 ,D正确.故选 CD.
11. 【解析】 因为简车按逆时针方向每旋转一周用时 秒,所以 ,故 A正确
因为当 时,盛水筒 位于点 ,所以 ,
所以有
,
因为 ,所以 ,即 ,
所以
,因此 B正确
由 可知:盛水筒 的纵坐标为 ,设它的横坐标为 ,
所以有 ,因为筒车旋转 秒时,所以此时盛水筒 在第一象限,
故 ,盛水筒 和初始点 的水平距离为 ,因此 不正确
因为 ,所以筒车在 秒的旋转过程中,第一次到达最高点需
要 秒,故 D正确.
12. 【 解析】圆锥 的内切球和外接球的球心重合 设为 ,则圆锥的轴截面为正三角形 ,
在 中, ,则 ,即 ,A正确,
设内切球的表面积 ,外接球的表面积为 ,则 ,B错误;
由于 ,即 , ,故
,C正确
设 的中点为 ,
连接 , ,则 ,易知 , ,
所以 ,所以
.
过 作 ,垂足为 ,
易知 ,则 ,
又 ,则 .
设平面 截球 所得截面圆的半径为 ,则
,
所以截面的面积为 .
13. 【解析】由题意, ,
当 时, ,解得 ,与 矛盾,故舍去;
当 时, ,解得 ,满足 ;
综上, ,故答案为 .
14. 【解析】由题意知 , ,则满足等式的 的最小值为 .
15.
【解析】取 的中点 ,连接 ,易知 ,又三棱柱 为正三棱柱,
平面 ,所以 为直线 与平面 所成角,
易得
故
将正三棱柱 补齐为正四棱柱 ,且底面为边长为 的菱形,
,直线 与直线 所成角即直线 与直线 所成的角,即
在 中,
,
故答案为:
; .
16. 【解析】根据题意, ,且 , ;
,
当 ,即 时,在 时, 取得最小值
;
又 ,
时, 取得最大值 ;
的取值范围是 ;
又 ;
,
解得 ;
;
当 ,即 时,
在 上是增函数,
的最小值是
,最大值是 ;
的值域是 ;
又 ;
;
解得 ;
综上, 的取值范围是
故答案为
17.解: 由角 的终边过点 得 ,
由角 的终边过点 ,得 ,
由
,得 .
,
当 时,
当 时, .
18.解: 由三月底面积增量几乎是二月的一倍,
根据幂函数,指数函数,对数函数增长快慢的比较,选择 比较合适;
由题意可得
,
,
;
由 知,一月底时水生植物的面积为 ;
假设 月后水生植物的面积是一月水生植物面积的 倍以上,即 ,
,
,因 ,即 ,
即 月份起是元旦开始研究时该水生植物面积的 倍以上.
19.解: 先证充分性 若 ,
则 即 ,
所以 ,故 三点共线;
再证必要性,若 三点共线,则存在实数 ,使得 ,
即
故 .
综上知,结论成立.
分别利用 和 共线的充要条件,得存在实数 使得,
,
即
,
则 ,解得 .
20.解: 在 中,由正弦定理得 ,
所以 .
因为 ,所以 ,
所以 为锐角,所以 .
在 中, , ,
,
所以 .
在 中,由余弦定理得 ,
所以
,
当且仅当 时等号成立,
所以 ,
所以 ,
即 面积的最大值为 .
21.解: 延长 , ,设 ,
连结 ,则直线 为平面 与平面 的交线.
作三棱锥 的侧面展开图,
连结 ,则 的周长最小值为 .
由题意可知 , , ,
由余弦定理得: ,解得
.
此时, ,故 BC 平面 .
22.解:
设 ,则
令 ,整理得: ,
故 ,且 ,得 .
所有
,
,
时, ,
时, ,
时, ,
时, , ,
所有
.
数学试卷
一、单选题(本大题共 8小题,共 40分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合 ,集合 ,则 ( )
A. B. C. D.
2. 若 是虚数单位 ,则 ( )
A. B. C. D.
3. 羽毛球运动是一项全民喜爱的体育运动,标准的羽毛球由 根羽毛固定在球托上,测得
每根羽毛在球托之外的长为 ,球托之外由羽毛围成的部分可看成一个圆台的侧面,测得
顶端所围成圆的直径是 ,底部所围成圆的直径是 ,据此可估算得球托之外羽毛所在
的曲面的展开图的圆心角为( )
A. B. C. D.
4. 设 是两条不同的直线, 是两个不同的平面,且直线 ,直线 ,则“ ”是
“ ”的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
5. 据你估计,一种商品在销售收入不变的条件下,其销量 与价格 之间的关系最可能是下
图中的( )
A. B.
C. D.
6. 现只有一把长为 的尺子,为了求得某小区草坪坛边缘 , 两点的距离 大于 ,
在草坪坛边缘找到点 与 ,已知 ,且 ,测得 ,
, ,则 ( )
A. B. C.
D.
7. 已知函数 , 为自然对数的底数 ,则 ( )
A. ,
B. ,当 时,
C. ,
D.
,当 时,
8. 已知把函数 的图象向左平移 后得到的图象关于 对称, 在
上具有单调性,则 的最大值为 ( )
A. B. C. D.
二、多选题(本大题共 4小题,共 20分。在每小题有多项符合题目要求)
9. 如图, 是正六边形 的中心,则 ( )
A. B.
C. D. 在 上的投影向量为
10. 已知函数 ,则下列结论正确的是 ( )
A. 函数 在 上不具有单调性 B. 不是周期函数
C. 函数 为偶函数 D. 当 时,函数 的最小值是
11. 筒车是我国古代发明的一种水利灌溉工具,既经济又环保,明朝科学家徐光启在《农政
全书》中用图画描绘了筒车的工作原理 图 假定在水流量稳定的情况下,筒车上的每一个盛
水筒都做匀速圆周运动 如图 ,将筒车抽象为一个半径为 的圆,设筒车按逆时针方向每旋转
一周用时 秒,当 ,盛水筒 位于点 ,经过 秒后运动到点 ,点 的
纵坐标满足 ,则下列叙述正确的是 ( )
A. 筒车转动的角速度
B. 当筒车旋转 秒时,盛水筒 对应的点 的纵坐标为
C. 当筒车旋转 秒时,盛水筒 和初始点 的水平距离为
D. 盛水筒 第一次到达最高点需要的时间是 秒
12. 圆锥内半径最大的球称为该圆锥的内切球 若圆锥的顶点和底面的圆周都在同一个球面
上,则称该球为圆锥的外接球 如图,圆锥 的内切球和外接球的球心重合,且圆锥 的底
面直径为 ,则( )
A. 设内切球的半径为 ,外接球的半径为 ,则
B. 设内切球的表面积 ,外接球的表面积为 ,则
C. 设圆锥的体积为 ,内切球的体积为 ,则
D. 设 , 是圆锥底面圆上的两点,且 ,则平面 截内切球所得截面的面积为
三、填空题(本大题共 4小题,共 20分)
13. 已知函数 ,若 ,则 .
14. 将曲线 上所有点向左平移 个单位,得到函数 的图象,则 的
最小值为 .
15. 已知正三棱柱 的各条棱长都是 ,则直线 与平面 所成角的正切
值为 直线 与直线 所成角的余弦值为 .
16. 若函数 满足对任意 ,都有 成立,则称函数 在区
间 上是“被 约束的”,若函数 在区间 上是“被
约束的”,则实数 的取值范围是 .
四、解答题(本大题共 6小题,共 70分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题 分 在平面直角坐标系中,已知角 的顶点与原点 重合,始边与 轴的非负半
轴重合,它的终边过点
求 的值.
若角 满足 ,求 的值.
18. 本小题 分 某校数学兴趣小组,在过去一年一直在研究学校附近池塘里某种水生植物
的面积变化情况,自 年元且开始测量该水生植物的面积,此后每隔一个月 每月月底 测
量一次,通过一年的观察发现,自 年元旦起,该水生植物在池塘里面积增加的速度是越
来越快的.最初测得该水生植物面积为 ,二月底测得该水生植物的面积为 ,三月底
测得该水生植物的面积为 ,该水生植物的面积 单位: 与时间 单位:月 的关系有
两个函数模型可供选择,一个是同学甲提出的 ;另一个是同学乙提出
的 ,记 年元旦最初测量时间 的值为 .
根据本学期所学,请你判断哪个同学提出的函数模型更适合?并求出该函数模型的解析式;
池塘中该水生植物面积应该在几月份起是元旦开始研究时该水生植物面积的 倍以上?
参考数据: ,
19. 本小题 分 已知 , , 是平面上不同的三点,点 是此平面上任意一点,则“ , , 三
点共线”的充要条件是“存在实数 ,使得 ” 此结论往往称为向量的爪
子模型.
给出这个结论的证明
在 的边 、 上分别取点 、 ,使 , ,连结 、 交于点
设 , 利用上述结论,求出用 、 表示向量 的表达式.
20. 本小题 分 如图,在四边形 中, , , ,连接
, .
求 的值;
若 , ,求 面积的最大值.
21. 本小题 分 正三棱锥 的侧面是底边长为 ,顶角为 的等腰三角形.过点
作这个三棱锥的截面 ,点 、 分别在棱 、 上.
如图,作出平面 与平面 的交线;
周长的最小值是否存在?若存在,求出其最小值,并指出此时直线 与平面 的
位置关系;若不存在,请说明理由.
22. 本小题 分 已知函数 , .
直接写出 的解集
若 ,其中 ,求 的取值范围;
己知 为正.整.数.,求
的最小值 用 表示 .
答案和解析
1. 【解析】由题设 , 或 ,
所以 .故选: .
2.
【解析】由 ,则 ,故选 C.
3. 【解析】由题意知:
上 上
,解得 .
下 下
4. 【解析】 , 是两条不同的直线, , 是两个不同的平面,且 , ,
由“ ”不可推出“ ”,即充分性不成立;
由“ ”不可推出“ ”,即必要性不成立;
故“ ”是“ ”既不充分又不必要条件,故选 D.
5. 【解析】 销售收入不变, 定值 , .故选 C.
6. 【解析】因为 , , ,所以 .
因为 ,所以 ,
所以
7. 【解析】由题意分别作出 , 图象如下图,
经过第一、二、三象限, 经过第一、二象限.
又 , 由指数函数增长速度可知 与 在第一象限必有 个交点.
,当 时, 一定成立.故选 D.
8. 【解析】设函数 的图象向左平移 后得到函数 ,
,
则 图象关于 对称,
所以 ,
即 ,
可得: ,
,
当 时,可得: ,
,
, ,
令 ,则 , ,
由正弦函数的性质可知, 在 上具有单调性,
此时该单调区间的区间长度为: .
在区间 具有单调性,
其区间长度必定不能超过 .
可得: ,
,
, ,
的最大值为 ,故选 B.
9. 【解析】对于 , ,则 错;
对于 ,
,
显然 B错误;
正六边形
,
则 ,
,故 C正确;
由 为正六边形,连接 ,可得 .
故 在 上的投影向量为 .
则 D正确.故选 CD.
10. 【解析】当 时, 在 上为增函数,当 时, 在 上减函数,A错误;
对于 , 定义域是 , ,因此 是函数的一个
周期,B错误;
对于 ,由 得 ,函数定义域是 ,关于原点对称,
,
, ,所以函数为偶函数, C正确;
对于 ,当 时,
在 上为减函数,在 上为增函数,
当 时, 取得最小值 ,D正确.故选 CD.
11. 【解析】 因为简车按逆时针方向每旋转一周用时 秒,所以 ,故 A正确
因为当 时,盛水筒 位于点 ,所以 ,
所以有
,
因为 ,所以 ,即 ,
所以
,因此 B正确
由 可知:盛水筒 的纵坐标为 ,设它的横坐标为 ,
所以有 ,因为筒车旋转 秒时,所以此时盛水筒 在第一象限,
故 ,盛水筒 和初始点 的水平距离为 ,因此 不正确
因为 ,所以筒车在 秒的旋转过程中,第一次到达最高点需
要 秒,故 D正确.
12. 【 解析】圆锥 的内切球和外接球的球心重合 设为 ,则圆锥的轴截面为正三角形 ,
在 中, ,则 ,即 ,A正确,
设内切球的表面积 ,外接球的表面积为 ,则 ,B错误;
由于 ,即 , ,故
,C正确
设 的中点为 ,
连接 , ,则 ,易知 , ,
所以 ,所以
.
过 作 ,垂足为 ,
易知 ,则 ,
又 ,则 .
设平面 截球 所得截面圆的半径为 ,则
,
所以截面的面积为 .
13. 【解析】由题意, ,
当 时, ,解得 ,与 矛盾,故舍去;
当 时, ,解得 ,满足 ;
综上, ,故答案为 .
14. 【解析】由题意知 , ,则满足等式的 的最小值为 .
15.
【解析】取 的中点 ,连接 ,易知 ,又三棱柱 为正三棱柱,
平面 ,所以 为直线 与平面 所成角,
易得
故
将正三棱柱 补齐为正四棱柱 ,且底面为边长为 的菱形,
,直线 与直线 所成角即直线 与直线 所成的角,即
在 中,
,
故答案为:
; .
16. 【解析】根据题意, ,且 , ;
,
当 ,即 时,在 时, 取得最小值
;
又 ,
时, 取得最大值 ;
的取值范围是 ;
又 ;
,
解得 ;
;
当 ,即 时,
在 上是增函数,
的最小值是
,最大值是 ;
的值域是 ;
又 ;
;
解得 ;
综上, 的取值范围是
故答案为
17.解: 由角 的终边过点 得 ,
由角 的终边过点 ,得 ,
由
,得 .
,
当 时,
当 时, .
18.解: 由三月底面积增量几乎是二月的一倍,
根据幂函数,指数函数,对数函数增长快慢的比较,选择 比较合适;
由题意可得
,
,
;
由 知,一月底时水生植物的面积为 ;
假设 月后水生植物的面积是一月水生植物面积的 倍以上,即 ,
,
,因 ,即 ,
即 月份起是元旦开始研究时该水生植物面积的 倍以上.
19.解: 先证充分性 若 ,
则 即 ,
所以 ,故 三点共线;
再证必要性,若 三点共线,则存在实数 ,使得 ,
即
故 .
综上知,结论成立.
分别利用 和 共线的充要条件,得存在实数 使得,
,
即
,
则 ,解得 .
20.解: 在 中,由正弦定理得 ,
所以 .
因为 ,所以 ,
所以 为锐角,所以 .
在 中, , ,
,
所以 .
在 中,由余弦定理得 ,
所以
,
当且仅当 时等号成立,
所以 ,
所以 ,
即 面积的最大值为 .
21.解: 延长 , ,设 ,
连结 ,则直线 为平面 与平面 的交线.
作三棱锥 的侧面展开图,
连结 ,则 的周长最小值为 .
由题意可知 , , ,
由余弦定理得: ,解得
.
此时, ,故 BC 平面 .
22.解:
设 ,则
令 ,整理得: ,
故 ,且 ,得 .
所有
,
,
时, ,
时, ,
时, ,
时, , ,
所有
.
同课章节目录
