人教版数学九年级下册 第二十八章 锐角三角函数 测试教学设计
文档属性
| 名称 | 人教版数学九年级下册 第二十八章 锐角三角函数 测试教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 22:03:11 | ||
图片预览

文档简介
第28章《锐角三角函数》测试教学设计
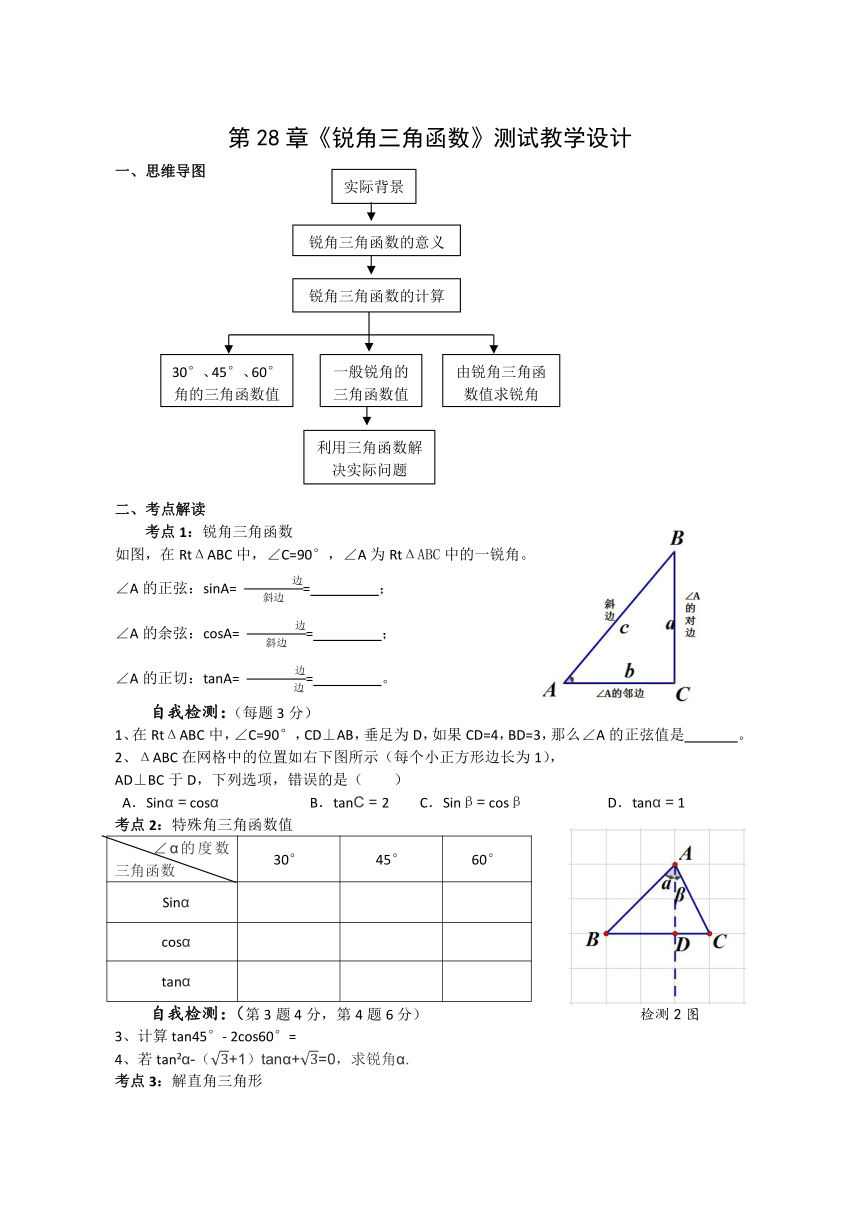
一、思维导图
二、考点解读
考点1:锐角三角函数
如图,在RtΔABC中,∠C=90°,∠A为RtΔABC中的一锐角。
∠A的正弦:sinA= = ;
∠A的余弦:cosA= = ;
∠A的正切:tanA= = 。
自我检测:(每题3分)
1、在RtΔABC中,∠C=90°,CD⊥AB,垂足为D,如果CD=4,BD=3,那么∠A的正弦值是 。
2、ΔABC在网格中的位置如右下图所示(每个小正方形边长为1),
AD⊥BC于D,下列选项,错误的是( )
A.Sinα = cosα B.tanC = 2 C.Sinβ= cosβ D.tanα = 1
考点2:特殊角三角函数值
∠α的度数三角函数 30° 45° 60°
Sinα
cosα
tanα
自我检测:(第3题4分,第4题6分) 检测2图
3、计算tan45°- 2cos60°=
4、若tan2α-(+1)tanα+=0,求锐角α.
考点3:解直角三角形
1. 由直角三角形中的已知元素求出其他已知元素的过程,叫做解直角三角形,
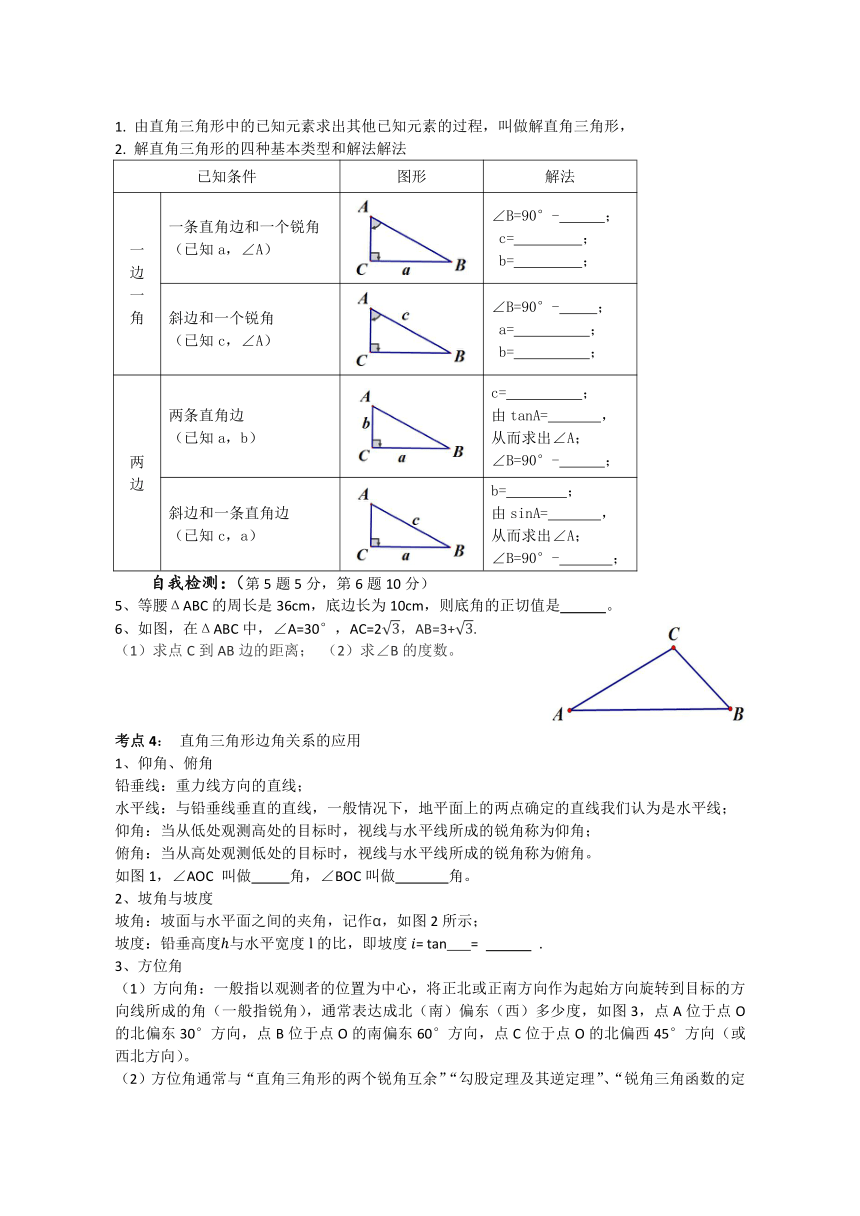
2. 解直角三角形的四种基本类型和解法解法
已知条件 图形 解法
一
边
一
角 一条直角边和一个锐角
(已知a,∠A) ∠B=90°- ;
c= ;
b= ;
斜边和一个锐角
(已知c,∠A) ∠B=90°- ;
a= ;
b= ;
两
边 两条直角边 (已知a,b) c= ;
由tanA= , 从而求出∠A;
∠B=90°- ;
斜边和一条直角边 (已知c,a) b= ;
由sinA= , 从而求出∠A;
∠B=90°- ;
自我检测:(第5题5分,第6题10分)
5、等腰ΔABC的周长是36cm,底边长为10cm,则底角的正切值是 。
6、如图,在ΔABC中,∠A=30°,AC=2,AB=3+.
(1)求点C到AB边的距离; (2)求∠B的度数。
考点4: 直角三角形边角关系的应用
1、仰角、俯角
铅垂线:重力线方向的直线;
水平线:与铅垂线垂直的直线,一般情况下,地平面上的两点确定的直线我们认为是水平线;
仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角;
俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角。
如图1,∠AOC 叫做 角,∠BOC叫做 角。
2、坡角与坡度
坡角:坡面与水平面之间的夹角,记作α,如图2所示;
坡度:铅垂高度与水平宽度的比,即坡度= tan = .
3、方位角
(1)方向角:一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度,如图3,点A位于点O的北偏东30°方向,点B位于点O的南偏东60°方向,点C位于点O的北偏西45°方向(或西北方向)。
(2)方位角通常与“直角三角形的两个锐角互余”“勾股定理及其逆定理”、“锐角三角函数的定义”和“特殊角的三角函数值”结合起来,解决数学和实际问题中的线段长度和角度大小问题。
图1 图2 图3
自我检测:(第7题10分,第8题10分)
7、据调查,超速行驶是引发交通事故的主要原因之一,小强用所学知识对一条笔直公路上的车辆进行测速.如图,观测点C到公路的距离CD=200 m,检测路段的起点A位于点C的南偏东60°方向,终点B位于点C的南偏东45°方向上,一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10 s,问此车是否超过了该路段16 m/s的限制速度 (观测点C离地面的距离忽略不计.参考数据:≈1.41,≈1.73 )
8、如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度 =1:的坡面AD走了200米到达D处,此时在D处测得山顶B的仰角为60°,求山高BC的值.(结果保留根号)
三、我的笔记(5分):
四、分层测试:(共10小题,共50分,限时15分钟;1-6题为ABC层必做题)
1.(4分)在RtΔABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
A. B. C. D.
2.(4分)如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
A. B. C. D. 第2题图
3.(4分)如图,电线杆CD的高度为,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一直线上)( )
A. B. C. D. ·cosα
4.(3分)如图,艘轮船在A处测得灯塔P位于其北偏东60方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30方向上,此时轮船与灯塔P的距离是( )
A. 15海里 B. 30海里 C. 45海里 D. 30海里
5.(4分)如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα = ,则小车上升的高度( )
A. 5米 B. 6米 C. 6.5米 D. 12米
第3题图 第4题图 第5题图
6.(10分)计算:(1)+(π-1)0-tan60° (2) - -tan45°
B层题
7.(10分)若锐角α满足2sin2α+3sinα-2=0,求α的度数.
B层题
8.(10分)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得
底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,
求该建筑物的高度BC的值.(结果保留整数,≈1.73)
A层题
9.(10分)如图是某小区的一个健身器材,已知BC=0.17m,AB=2.50m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m)).(参考数据:sin70°≈0.94,cos70°≈0.34 ,tan70°≈2.75)
A层题
10.(10分)为了保证端午龙舟赛在我市长江某水域顺利举办,某部门工作人员乘快艇到该水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示.求建筑物P到赛道AB的距离.(结果保留根号)
五、订正及反思(5分):
一、思维导图
二、考点解读
考点1:锐角三角函数
如图,在RtΔABC中,∠C=90°,∠A为RtΔABC中的一锐角。
∠A的正弦:sinA= = ;
∠A的余弦:cosA= = ;
∠A的正切:tanA= = 。
自我检测:(每题3分)
1、在RtΔABC中,∠C=90°,CD⊥AB,垂足为D,如果CD=4,BD=3,那么∠A的正弦值是 。
2、ΔABC在网格中的位置如右下图所示(每个小正方形边长为1),
AD⊥BC于D,下列选项,错误的是( )
A.Sinα = cosα B.tanC = 2 C.Sinβ= cosβ D.tanα = 1
考点2:特殊角三角函数值
∠α的度数三角函数 30° 45° 60°
Sinα
cosα
tanα
自我检测:(第3题4分,第4题6分) 检测2图
3、计算tan45°- 2cos60°=
4、若tan2α-(+1)tanα+=0,求锐角α.
考点3:解直角三角形
1. 由直角三角形中的已知元素求出其他已知元素的过程,叫做解直角三角形,
2. 解直角三角形的四种基本类型和解法解法
已知条件 图形 解法
一
边
一
角 一条直角边和一个锐角
(已知a,∠A) ∠B=90°- ;
c= ;
b= ;
斜边和一个锐角
(已知c,∠A) ∠B=90°- ;
a= ;
b= ;
两
边 两条直角边 (已知a,b) c= ;
由tanA= , 从而求出∠A;
∠B=90°- ;
斜边和一条直角边 (已知c,a) b= ;
由sinA= , 从而求出∠A;
∠B=90°- ;
自我检测:(第5题5分,第6题10分)
5、等腰ΔABC的周长是36cm,底边长为10cm,则底角的正切值是 。
6、如图,在ΔABC中,∠A=30°,AC=2,AB=3+.
(1)求点C到AB边的距离; (2)求∠B的度数。
考点4: 直角三角形边角关系的应用
1、仰角、俯角
铅垂线:重力线方向的直线;
水平线:与铅垂线垂直的直线,一般情况下,地平面上的两点确定的直线我们认为是水平线;
仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角;
俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角。
如图1,∠AOC 叫做 角,∠BOC叫做 角。
2、坡角与坡度
坡角:坡面与水平面之间的夹角,记作α,如图2所示;
坡度:铅垂高度与水平宽度的比,即坡度= tan = .
3、方位角
(1)方向角:一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度,如图3,点A位于点O的北偏东30°方向,点B位于点O的南偏东60°方向,点C位于点O的北偏西45°方向(或西北方向)。
(2)方位角通常与“直角三角形的两个锐角互余”“勾股定理及其逆定理”、“锐角三角函数的定义”和“特殊角的三角函数值”结合起来,解决数学和实际问题中的线段长度和角度大小问题。
图1 图2 图3
自我检测:(第7题10分,第8题10分)
7、据调查,超速行驶是引发交通事故的主要原因之一,小强用所学知识对一条笔直公路上的车辆进行测速.如图,观测点C到公路的距离CD=200 m,检测路段的起点A位于点C的南偏东60°方向,终点B位于点C的南偏东45°方向上,一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10 s,问此车是否超过了该路段16 m/s的限制速度 (观测点C离地面的距离忽略不计.参考数据:≈1.41,≈1.73 )
8、如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度 =1:的坡面AD走了200米到达D处,此时在D处测得山顶B的仰角为60°,求山高BC的值.(结果保留根号)
三、我的笔记(5分):
四、分层测试:(共10小题,共50分,限时15分钟;1-6题为ABC层必做题)
1.(4分)在RtΔABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
A. B. C. D.
2.(4分)如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
A. B. C. D. 第2题图
3.(4分)如图,电线杆CD的高度为,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一直线上)( )
A. B. C. D. ·cosα
4.(3分)如图,艘轮船在A处测得灯塔P位于其北偏东60方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30方向上,此时轮船与灯塔P的距离是( )
A. 15海里 B. 30海里 C. 45海里 D. 30海里
5.(4分)如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα = ,则小车上升的高度( )
A. 5米 B. 6米 C. 6.5米 D. 12米
第3题图 第4题图 第5题图
6.(10分)计算:(1)+(π-1)0-tan60° (2) - -tan45°
B层题
7.(10分)若锐角α满足2sin2α+3sinα-2=0,求α的度数.
B层题
8.(10分)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得
底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,
求该建筑物的高度BC的值.(结果保留整数,≈1.73)
A层题
9.(10分)如图是某小区的一个健身器材,已知BC=0.17m,AB=2.50m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m)).(参考数据:sin70°≈0.94,cos70°≈0.34 ,tan70°≈2.75)
A层题
10.(10分)为了保证端午龙舟赛在我市长江某水域顺利举办,某部门工作人员乘快艇到该水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示.求建筑物P到赛道AB的距离.(结果保留根号)
五、订正及反思(5分):
