离散型随机变量2[上学期]
图片预览




文档简介
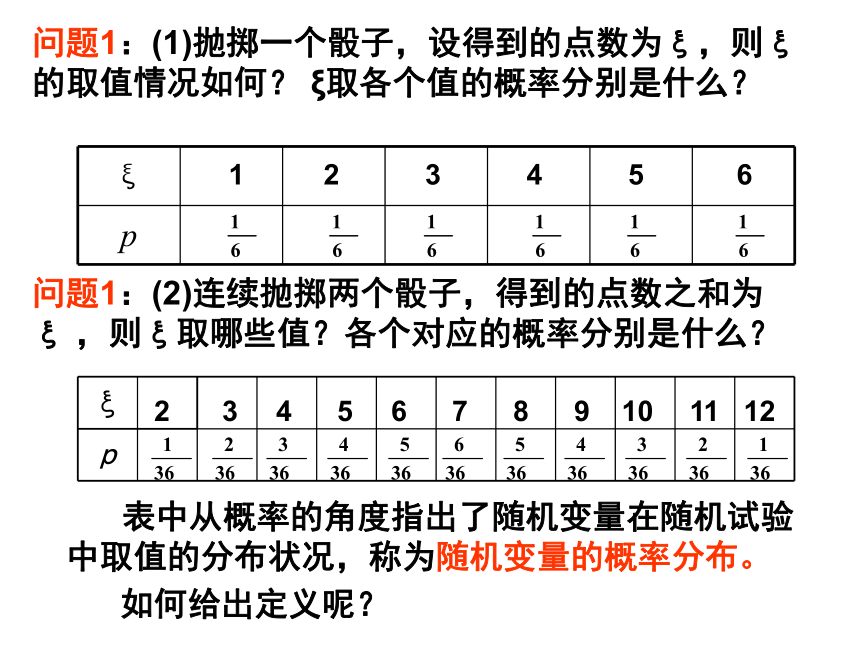
课件19张PPT。离散型随机变量的分布列(2)问题1:(1)抛掷一个骰子,设得到的点数为ξ,则ξ的取值情况如何? ξ取各个值的概率分别是什么?213456问题1:(2)连续抛掷两个骰子,得到的点数之和为ξ ,则ξ取哪些值?各个对应的概率分别是什么?42356789101112 表中从概率的角度指出了随机变量在随机试验中取值的分布状况,称为随机变量的概率分布。如何给出定义呢?离散型随机变量的分布列称为随机变量ξ的概率分布,简称ξ的分布列。则表:ξ取每一个值 的概率 设离散型随机变量ξ可能取的值为1、概率分布(分布列) 根据随机变量的意义与概率的性质,你能得出分布列有什么性质?离散型随机变量的分布列具有下述两个性质:求离散型随机变量的概率分布的方法步骤:1、找出随机变量ξ的所有可能的取值2、求出各取值的概率3、列成表格。 根据射手射击所得环数ξ 的分布列,有例1. 某一射手射击所得环数ξ 的分布列如下:求此射手”射击一次命中环数≥7”的概率. 分析: ”射击一次命中环数≥7”是指互斥事件”ξ=7”, ”ξ=8”, ”ξ=9”, ”ξ=10” 的和.解:P(ξ=7)=0.09,P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22,所求的概率为P(ξ≥7)=0.09+ 0.28+ 0.29+ 0.22= 0.88练习1.一个类似于细胞分裂的物体,一次分裂为二,两次分裂为四,如此进行有限多次,而随机终止,设分裂n次终止的概率是 (n=1,2,3,……)记ξ为原物体在分裂终止后所生成的子块数目,求P(ξ≤10).解:依题意,原物体在分裂终止后所生成的数目ξ的分布列为说明:一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.问题2:重复抛掷骰子 n 次,(2点)向上的次数ξ
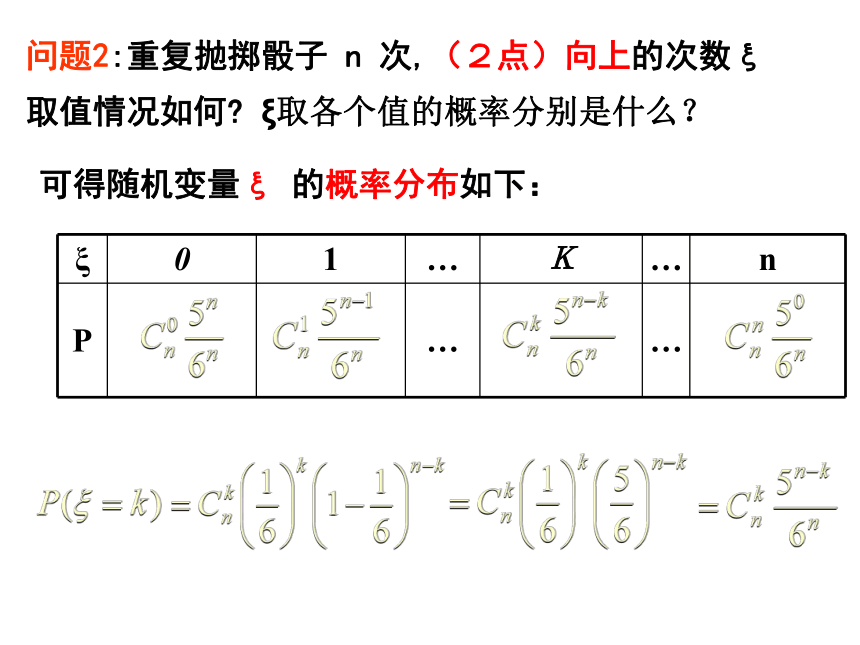
取值情况如何? ξ取各个值的概率分别是什么? 可得随机变量ξ 的概率分布如下: 服从二项分布, ξ的概率分布如下:(重复抛掷骰子 n 次,得到2点的次数)ξ 记作ξ~B(n, ),并记:问题2:重复抛掷骰子 n 次,(2点)向上的次数ξ
取值情况如何? ξ取各个值的概率分别是什么? ξ服从二项分布, 又如:重复抛掷一枚硬币 n 次,出现正面向上的次数ξ, 记作ξ~B(n, ),并记:2.二项分布 如果在一次试验中某事件发生的概率是 p,那么在 n 次独立重复试验中这个事件恰好发生 k 次的概率是 设在 n 次独立重复试验中某个事件 A 发生的次数ξ, ξ是一个随机变量. 于是可得随机变量ξ 的概率分布如下: 记作ξ~B(n,p),其中n,p为参数,并记: 所以,称这样的随机变量ξ服从二项分布, 随机变量ξ 的概率分布如下:由于恰好是二项展开式 ξ的概率分布如下:问题3:重复抛掷骰子 ,(2点)第一次向上的实验次
数ξ取值情况如何? ξ取各个值的概率分别是什么? ξ 1 2 3 … k …
P 称ξ服从几何分布,并记g(k,1/6)=1/6·(5/6)k-13.几何分布在独立重复试验中,某事件A第一次发生时所作的试验次数ξ也是一个取值为正整数的随机变量。 “ξ =k”表示在第k次独立重复试验时事件A第一次发生。如果把第k次实验时事件A发生记为Ak, p( Ak )=p,那么于是得到随机变量ξ的概率分布如下:(k=0,1,2…,q=1-p.)称ξ服从几何分布,并记g(k,p)=p·qk-1 ξ 1 2 3 … k …
P 例 2. 某人射击击中目标的概率是0.2,射击中每次
射击的结果是相互独立的,求他在10次射击中击中目标的次数不超过5次的概率(精确到0.01)。例 3. 某人每次投篮投中的概率为0.1,各次投篮的结果互相独立。求他首次投篮投中时投篮次数的分布列,以及他在5次内投中的概率(精确到0.01)。练习2.(1)(2000年高考题)某厂生产电子元件,其产品的次品率为5%.现从一批产品中任意地连续取出2件,写出其中次品数ξ的概率分布.(2).1名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在交通岗遇到红灯的事件是独立的,并且概率都是1/3.(1)求这名学生在途中遇到红灯的次数ξ的分布列.(2)求这名学生在途中至少遇到一次红灯的概率.练习3、在一袋中装有一只红球和九只白球。每次从袋中任取一球取后放回,直到取得红球为止,求取球次数ξ的分布列。分析:袋中虽然只有10个球,由于每次任取一球,取后又放回,因此应注意以下几点:
(1)一次取球两个结果:取红球A或取白球ā,且P(A)=0.1;
(2)取球次数ξ可能取1,2,…;
(3)由于取后放回。因此,各次取球相互独立。小结1. 离散型随机变量的分布列2.离散型随机变量的分布列的两个性质: 一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。3.二项分布 在 n 次独立重复试验中某个事件发生的次数ξ是一个随机变量. 这个事件恰好发生 k 次的概率是 (其中 q=1-p ).即ξ服从二项分布, 记作ξ~B(n,p),作业同步作业本第2页。
取值情况如何? ξ取各个值的概率分别是什么? 可得随机变量ξ 的概率分布如下: 服从二项分布, ξ的概率分布如下:(重复抛掷骰子 n 次,得到2点的次数)ξ 记作ξ~B(n, ),并记:问题2:重复抛掷骰子 n 次,(2点)向上的次数ξ
取值情况如何? ξ取各个值的概率分别是什么? ξ服从二项分布, 又如:重复抛掷一枚硬币 n 次,出现正面向上的次数ξ, 记作ξ~B(n, ),并记:2.二项分布 如果在一次试验中某事件发生的概率是 p,那么在 n 次独立重复试验中这个事件恰好发生 k 次的概率是 设在 n 次独立重复试验中某个事件 A 发生的次数ξ, ξ是一个随机变量. 于是可得随机变量ξ 的概率分布如下: 记作ξ~B(n,p),其中n,p为参数,并记: 所以,称这样的随机变量ξ服从二项分布, 随机变量ξ 的概率分布如下:由于恰好是二项展开式 ξ的概率分布如下:问题3:重复抛掷骰子 ,(2点)第一次向上的实验次
数ξ取值情况如何? ξ取各个值的概率分别是什么? ξ 1 2 3 … k …
P 称ξ服从几何分布,并记g(k,1/6)=1/6·(5/6)k-13.几何分布在独立重复试验中,某事件A第一次发生时所作的试验次数ξ也是一个取值为正整数的随机变量。 “ξ =k”表示在第k次独立重复试验时事件A第一次发生。如果把第k次实验时事件A发生记为Ak, p( Ak )=p,那么于是得到随机变量ξ的概率分布如下:(k=0,1,2…,q=1-p.)称ξ服从几何分布,并记g(k,p)=p·qk-1 ξ 1 2 3 … k …
P 例 2. 某人射击击中目标的概率是0.2,射击中每次
射击的结果是相互独立的,求他在10次射击中击中目标的次数不超过5次的概率(精确到0.01)。例 3. 某人每次投篮投中的概率为0.1,各次投篮的结果互相独立。求他首次投篮投中时投篮次数的分布列,以及他在5次内投中的概率(精确到0.01)。练习2.(1)(2000年高考题)某厂生产电子元件,其产品的次品率为5%.现从一批产品中任意地连续取出2件,写出其中次品数ξ的概率分布.(2).1名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在交通岗遇到红灯的事件是独立的,并且概率都是1/3.(1)求这名学生在途中遇到红灯的次数ξ的分布列.(2)求这名学生在途中至少遇到一次红灯的概率.练习3、在一袋中装有一只红球和九只白球。每次从袋中任取一球取后放回,直到取得红球为止,求取球次数ξ的分布列。分析:袋中虽然只有10个球,由于每次任取一球,取后又放回,因此应注意以下几点:
(1)一次取球两个结果:取红球A或取白球ā,且P(A)=0.1;
(2)取球次数ξ可能取1,2,…;
(3)由于取后放回。因此,各次取球相互独立。小结1. 离散型随机变量的分布列2.离散型随机变量的分布列的两个性质: 一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。3.二项分布 在 n 次独立重复试验中某个事件发生的次数ξ是一个随机变量. 这个事件恰好发生 k 次的概率是 (其中 q=1-p ).即ξ服从二项分布, 记作ξ~B(n,p),作业同步作业本第2页。
